
L
ABORATORIUM FIZYCZNE
Instytut Fizyki Politechniki Krakowskiej
Obliczanie i wyrażanie niepewności pomiaru
wersja rozszerzona
opracował: Jan Kurzyk

Obliczanie i wyrażanie niepewności pomiarowych
2
Spis treści
1.
WPROWADZENIE ..................................................................................................................................... 4
2.
BŁĄD POMIARU ....................................................................................................................................... 5
2.1
B
ŁĘDY PRZYPADKOWE
.................................................................................................................................. 5
2.2
B
ŁĘDY SYSTEMATYCZNE
................................................................................................................................ 5
2.3
B
ŁĘDY GRUBE
............................................................................................................................................. 7
3.
NIEPEWNOŚĆ POMIARU .......................................................................................................................... 8
3.1
N
IEPEWNOŚĆ STANDARDOWA
....................................................................................................................... 8
3.2
N
IEPEWNOŚĆ ROZSZERZONA
......................................................................................................................... 9
4.
POMIARY BEZPOŚREDNIE I POŚREDNIE.................................................................................................... 9
5.
OCENA NIEPEWNOŚCI STANDARDOWEJ POMIARU BEZPOŚREDNIEGO .................................................. 10
5.1
O
CENA NIEPEWNOŚCI STANDARDOWEJ METODĄ
A .......................................................................................... 10
5.2
O
CENA NIEPEWNOŚCI STANDARDOWEJ METODĄ
B .......................................................................................... 15
5.2.1
Przedział graniczny .......................................................................................................................... 15
5.2.2
Proste przyrządy mechaniczne ........................................................................................................ 17
5.2.3
Analogowe mierniki elektryczne ...................................................................................................... 20
5.2.4
Elektroniczne mierniki cyfrowe ........................................................................................................ 23
5.3
S
UMOWANIE SKŁADNIKÓW NIEPEWNOŚCI
...................................................................................................... 24
6.
OCENA NIEPEWNOŚCI STANDARDOWEJ POMIARU POŚREDNIEGO ........................................................ 25
6.1
F
UNKCJA BĘDĄCA SUMĄ ZMIENNYCH NIEZALEŻNYCH
........................................................................................ 27
6.2
F
UNKCJA BĘDĄCA ILOCZYNEM POTĘG ZMIENNYCH NIEZALEŻNYCH
....................................................................... 27
7.
PODAWANIE WYNIKU POMIARU ........................................................................................................... 29
7.1
C
YFRY ZNACZĄCE
...................................................................................................................................... 29
7.2
Z
AOKRĄGLENIA WYNIKÓW POMIARU
............................................................................................................ 30
7.3
S
TOSOWANIE JEDNOSTEK WTÓRNYCH
........................................................................................................... 31
7.4
P
ODAWANIE WYNIKU POMIARU
,
GDY MIARĄ NIEPEWNOŚCI JEST NIEPEWNOŚĆ STANDARDOWA
................................ 32
7.5
P
ODAWANIE WYNIKU POMIARU
,
GDY MIARĄ NIEPEWNOŚCI JEST NIEPEWNOŚĆ ROZSZERZONA
.................................. 32
8.
UŚREDNIANIE WYNIKÓW ....................................................................................................................... 33
9.
PORÓWNYWANIE WYNIKÓW ................................................................................................................ 33
10.
OPRACOWYWANIE WYNIKÓW POMIARU WIELKOŚCI ZALEŻNYCH .................................................... 34
10.1
G
RAFICZNA PREZENTACJA WYNIKÓW
............................................................................................................ 34
10.2
R
EGRESJA LINIOWA
................................................................................................................................... 35
DODATEK A. OPIS PROGRAMU WYKRESLAB ................................................................................................... 38
DODATEK B. PRZEPIS OBLICZANIA NIEPEWNOŚCI POMIAROWYCH ............................................................... 42
1.
OBLICZANIE NIEPEWNOŚCI POMIARÓW BEZPOŚREDNICH ..................................................................... 42
1.1
O
BLICZANIE NIEPEWNOŚCI STANDARDOWEJ METODĄ
A .................................................................................... 42
1.2
O
BLICZANIE NIEPEWNOŚCI STANDARDOWEJ METODĄ
B .................................................................................... 42
1.2.1
Opis ogólny ...................................................................................................................................... 42
1.2.2
Obliczanie niepewności standardowej wynikającej z dokładności przyrządu pomiarowego .......... 43
2.
SUMOWANIE SKŁADNIKÓW NIEPEWNOŚCI ........................................................................................... 44

Wprowadzenie do metod opracowywania danych pomiarowych
3
3.
OBLICZANIE NIEPEWNOŚCI POMIARÓW POŚREDNICH ........................................................................... 44
DODATEK C. PRZYKŁAD OPRACOWANIA DANYCH POMIAROWYCH POMIARU WARTOŚCI PRZYŚPIESZENIA
ZIEMSKIEGO METODĄ WAHADŁA PROSTEGO. ............................................................................................... 46
1.
ANALIZA POMIARU OKRESU DRGAŃ WAHADŁA. ................................................................................... 47
2.
ANALIZA POMIARU DŁUGOŚCI WAHADŁA ............................................................................................. 48
2.1
A
NALIZA POMIARU DŁUGOŚCI NICI
................................................................................................................ 48
2.2
A
NALIZA POMIARU ŚREDNICY KULKI
.............................................................................................................. 48
3.
ANALIZA POMIARU WARTOŚCI PRZYŚPIESZENIA ZIEMSKIEGO ............................................................... 49
4.
PRZYKŁAD ANALIZY WYNIKÓW PROWADZĄCYCH DO WARTOŚCI NIEZGODNEJ Z WARTOŚCIĄ
TABLICOWĄ.................................................................................................................................................... 51
LITERATURA ................................................................................................................................................... 53

Obliczanie i wyrażanie niepewności pomiarowych
4
Obliczanie i wyrażanie niepewności pomiarowych
Jan Kurzyk
1.
Wprowadzenie
W wielu dziedzinach nauki i techniki staramy się ilościowo opisywać zjawiska oraz cechy ba-
danych obiektów. W przypadku właściwości fizycznych zjawisk lub obiektów, do ich opisu używamy
tzw.
wielkości fizycznych
. Przykładowymi wielkościami fizycznymi są np. długość (jakiegoś obiektu),
czas (trwania jakiegoś zjawiska) czy natężenie prądu elektrycznego. Aby móc porównywać wielkości
fizyczne (tego samego typu) musimy im w sposób jednoznaczny przypisać wartości liczbowe. Liczby te
określają ile razy dana wielkość fizyczna jest większa (lub mniejsza) od jej
jednostki miary
, czyli wiel-
kości fizycznej (tego samego typu co wielkość mierzona), której umownie przypisaliśmy wartość 1.
Proces mający na celu znalezienie wartości danej wielkości fizycznej (jako iloczynu liczby określającej
wartość tej wielkości fizycznej i jej jednostki miary) nazywamy
pomiarem
. W ogólności wynik pomiaru
jest tylko estymatą (oszacowaniem) wartości mierzonej. Dlatego podając wynik pomiaru musimy
podać jednocześnie ilościową informację o jakości podanego wyniku. Dopiero wtedy będziemy mogli
określić jego wiarygodność lub porównać z innym wynikiem. Miarą tej wiarygodności jest wartość
tzw.
niepewności pomiaru
, którą podajemy w tych samych jednostkach miary, co wynik pomiaru.
Wartość niepewności w połączeniu z wartością zmierzoną, pozwala nam wyznaczyć przedział, w któ-
rym z określonym prawdopodobieństwem, nazywanym
poziomem ufności
mieści się rzeczywista war-
tość mierzonej wielkości. Należy podkreślić, że niepewność pomiarowa nie jest wielkością fizyczną i w
związku z tym nie da się jej zmierzyć. Metodami wyznaczania niepewności pomiarowej zajmuje się
tzw. teoria niepewności pomiaru. Ponieważ niepewność pomiarowa nie może być jednoznacznie
zdefiniowana (nie jest to wielkość fizyczna), teoria opisująca procedury wyznaczania niepewności
pomiaru w dużej mierze opiera się na międzynarodowych umowach. Metody określania niepewności
pomiaru opisywane przez teorię niepewności pomiaru nie ograniczają się jedynie do fizyki. Stosowa-
ne są one we wszystkich dziedzinach nauki i techniki stosujących pomiar jako źródło informacji. Za-
równo procedury obliczania niepewności, jak i samo nazewnictwo stosowane w teorii niepewności
ewoluuje. Społeczność naukowa od dawna dążyła do ujednolicenia nazewnictwa i metod wyznacza-
nia niepewności pomiarów. W 1980 roku została powołana Grupa Robocza do spraw Określania Nie-
pewności. Wynikiem prac członków Grupy Roboczej, wytypowanych przez Międzynarodowe Biuro
Miar
1
, Międzynarodową Komisję Elektrotechniczną
2
, Międzynarodową Organizację Normalizacyjną
3
i
Międzynarodową Organizacje Metrologii Prawnej
4
jest wydany w 1993 roku przez ISO dokument:
Guide to the Expression of Uncertainty Measurement [1]. Dokument ten zawiera zalecenia dotyczące
wyrażania niepewności pomiaru. Polskie tłumaczenie tego dokumentu zostało wydane przez Główny
Urząd Miar w 1999 roku pod tytułem Wyrażanie niepewności pomiaru. Przewodnik [2]. W dalszej
części tego tekstu będziemy często powoływali się na ten dokument nazywając go w skrócie Prze-
wodnikiem.
1
BIPM – Bueaur International des Poids et Mesures.
2
IEC – International Electrotechnical Commission.
3
ISO – International Organization for Standarization.
4
OIML – International Organization of Legal Metrology.

Wprowadzenie do metod opracowywania danych pomiarowych
5
2.
Błąd pomiaru
Niedoskonałości pomiaru powodują, ze wynik pomiaru różni się od rzeczywistej wartości wielko-
ści mierzonej. Różnicę między wartością zmierzoną a wartością rzeczywistą
nazywamy błędem
pomiaru
łą
= − .
(2.1)
Oczywiście wartości rzeczywistej nigdy nie znamy, ale w praktyce możemy jej wartość utożsamiać z
wynikiem pomiaru wykonanego za pomocą metody znacznie dokładniejszej niż nasza. Dla przykładu
wykonując w laboratorium studenckim pomiar wartości jakiejś stałej fizycznej, możemy za wartość
rzeczywistą przyjąć wartość tej stałej wziętą z tablic fizycznych.
Błędy pomiaru mogą mieć charakter systematyczny lub przypadkowy.
2.1
Błędy przypadkowe
Przyjmuje się, ze
błędy przypadkowe
wynikają z tego, że wielkości mające wpływ na wynik
pomiaru nie mają stałych wartości w czasie wykonywania pomiaru, lecz zmieniają się w sposób nie-
przewidywalny (przypadkowy, stochastyczny). Czynniki wywołujące te zmiany nazywamy
oddziały-
waniem przypadkowym
. Efektem działania tych czynników są zmiany wyników powtarzanych obser-
wacji mierzonej wielkości (kolejny wynik pomiaru może różnić się od poprzedniego). Innymi słowy
błędy przypadkowe prowadzą do rozrzutu wyników pomiaru, przy czym szansa uzyskania wyniku
mniejszego niż wartość rzeczywista jest porównywalna z szansą uzyskania wyniku większego. A zatem
wyniki pomiarów są rozrzucone wokół wartości rzeczywistej (patrz rysunek 1.1. a). Najczęściej, naj-
lepszym oszacowaniem wartości wielkości mierzonej jest
średnia arytmetyczna
otrzymanych wyni-
ków pomiaru, czyli suma tych wartości podzielona przez ich liczbę. Błąd takiego pomiaru jest różnicą
między wartością średnią arytmetyczną i wartością rzeczywistą. Wartości tego błędu nie znamy, ale
możemy go zmniejszyć poprzez zwiększenie liczby pomiarów. Błąd tego typu maleje do zera, gdy
liczba pomiarów dąży do nieskończoności.
x
x
x
0
x
a)
b)
c)
Rys. 2.1. Schematycznie przedstawione wyniki pomiarów dla różnych przypadków błędów pomia-
ru. Wyniki pomiarów reprezentowane są przez niebieskie krzyżyki. Zielona przerywana linia re-
prezentuje wartość rzeczywistą. a) rozrzut wyników pomiaru wywołany błędami przypadkowymi.
b) systematyczny błąd pomiaru w przypadku braku błędów przypadkowych. c) połączenie błędu
systematycznego z błędami przypadkowymi.
2.2
Błędy systematyczne
W przeciwieństwie do czynników odpowiedzialnych za powstawanie błędów przypadkowych,
czynnik lub czynniki prowadzące do
błędu systematycznego
(tzw.
oddziaływanie systematyczne
) mają

Obliczanie i wyrażanie niepewności pomiarowych
6
w każdym pomiarze taki sam wpływ na wynik pomiaru. Jeśli podczas pomiarów z oddziaływaniem
systematycznym nie występują oddziaływania przypadkowe (wszystkie wyniki pomiaru są jednako-
we), to różnica między wartością zmierzoną a rzeczywistą jest stała i równa błędowi systematyczne-
mu (patrz rysunek 2.1. b). Jeśli na oddziaływania systematyczne nakładają się oddziaływania przypad-
kowe, to wyniki pomiarów nie będą rozrzucone wokół wartości rzeczywistej, lecz wokół wartości
przesuniętej względem wartości rzeczywistej o wartość błędu systematycznego (patrz rysunek 2.1. c).
Gdybyśmy w tym przypadku wykonali bardzo dużą liczbę pomiarów eliminując w ten sposób błąd
przypadkowy, to różnica miedzy średnią arytmetyczną wyników pomiarów i wartością rzeczywistą
byłaby równa błędowi systematycznemu.
Jeśli znamy przyczynę błędu systematycznego (lub błędów systematycznych), to powinniśmy
ją usunąć lub jeśli to nie jest możliwe określić ilościowo wpływ oddziaływania systematycznego na
wynik pomiaru i skompensować ten wpływ wprowadzając odpowiednią
poprawkę
. Może to być po-
prawka addytywna (do wyniki musimy dodać poprawkę) lub multiplikatywna (wynik musimy prze-
mnożyć przez odpowiedni współczynnik) lub obie poprawki jednocześnie.
Przykład 1
Wykonano pomiar natężenia prądu elektrycznego analogowym amperomierzem, który nie
został wyzerowany, czyli pokazuje niezerową wartość prądu elektrycznego w sytuacji, gdy prąd w
obwodzie nie płynie. W takim przypadku każdy pomiar będzie obarczony błędem systematycznym
równym . W celu usunięcia tego błędu powinniśmy wyzerować ten amperomierz lub zastąpić go
innym sprawnym, zaś w ostateczności możemy skompensować ten błąd przez zastosowanie addy-
tywnej poprawki, czyli w tym przypadku odjęcie od każdego wyniku pomiaru wartości .
Przykład 2
Wykonano pomiar długości jakiegoś dużego obiektu metalową taśmą mierniczą w tempera-
turze znacznie odbiegającej od temperatury wzorcowania tej taśmy podanej przez producenta. Wia-
domo, że długość taśmy zmienia się wraz z temperaturą. Załóżmy, że wystarczająco dobre jest przy-
bliżenie liniowej zależności zmiany długości taśmy ze zmianą temperatury. Wówczas długość od-
cinka taśmy w temperaturze wynosi
=
1 + Δ ,
gdzie
jest współczynnikiem rozszerzalności liniowej materiału, z którego wykonano taśmę,
Δ = − , różnicą między temperaturą , w której wykonywano pomiar, a temperaturą , w
której wzorcowana była taśma miernicza. Powinniśmy uwzględnić fakt zmiany wymiarów taśmy
wprowadzając multiplikatywnie współczynnik poprawkowy, czyli w tym przypadku podzielić każdy
wynik pomiaru przez czynnik
1 + Δ
Jak widzimy znajomość czynników systematycznych pozwala na skompensowanie błędu sys-
tematycznego
5
. Jednak wpływ oddziaływań systematycznych, których nie jesteśmy świadomi może
prowadzić do tego, że wyniki pomiaru będą znacznie odbiegać od wartości rzeczywistej. Taka sytua-
cja zdarza się nawet wybitnym eksperymentatorom. Jako przykład przyjrzyjmy się wykresowi na Ry-
5
Zauważmy, że w przypadku czynników przypadkowych nie jest możliwe wprowadzenie poprawki, która skom-
pensowałaby błędy przypadkowe.

Wprowadzenie do metod opracowywania danych pomiarowych
7
sunku 2.2, który przedstawia wyniki niektórych pomiarów prędkości światła wykonanych w ubiegłym
wieku przez znane ośrodki badawcze. Czarne kółeczka są punktami pomiarowymi, a pionowe kreski
obrazują przedziały, które zgodnie z analizą danych pomiarowych powinny były zawierać rzeczywistą
wartość prędkości światła. Jak widzimy aktualnie uznana za poprawną wartość prędkości światła nie
mieści się w dużej części tych przedziałów zwłaszcza dla pomiarów z lat 30. i 40. ubiegłego wieku.
Powodem tego były błędy systematyczne metody pomiarowej, których eksperymentatorzy byli nie-
świadomi.
Rys. 2.2. Wyniki pomiarów prędkości światła w latach 1920-1975. (źródło: A.K.Wróblewski,
J.A.Zakrzewski, Wstęp do fizyki, tom 1).
2.3
Błędy grube
Oprócz dwóch typów błędów wymienionych powyżej możemy jeszcze wyróżnić tzw.
błędy
grube
zwane również pomyłkami. Powstają one głównie na skutek pomyłek w odczycie lub zapisie
wyników pomiaru, niewłaściwego użycia przyrządu, błędach w obliczeniach, stosowaniu niewłaści-
wych jednostek miar itp. Tego typu błędy prowadzą na ogół do bardzo drastycznych różnic między
wynikiem pomiaru a wartością rzeczywistą przez co są stosunkowo łatwo zauważalne, a tym samym
łatwe do usunięcia.
Wykonując pomiar powinniśmy unikać sytuacji, w których sami stajemy się źródłem błędów
wynikających z niestarannego wykonywania pomiarów. Przykładem może być tzw. błąd paralaksy.
Spójrzmy na rysunek 2.3. Na obu zdjęciach mamy dokładnie to same wskazanie przyrządu, tyle, że na
zdjęciu (b) odczytu dokonano patrząc na wskazówkę pod niewłaściwym kątem (proszę zwrócić uwagę
na wskazówkę i jej odbicie w lusterku umieszczonym na skali przyrządu) przez co popełniono tzw.
błąd paralaksy.
(a)
(b)
Rys. 2.3. Prawidłowy (a) i nieprawidłowy (b) odczyt wskazań przyrządu. w przypadku (b) popeł-
niamy tzw. błąd paralaksy.

Obliczanie i wyrażanie niepewności pomiarowych
8
Niepewność pomiaru jest parametrem związanym z rezultatem pomiaru, charakteryzują-
cym rozrzut wartości, które można w uzasadniony sposób przypisać wielkości mierzonej.
3.
Niepewność pomiaru
Termin
niepewność pomiaru
jest używany w dwóch znaczeniach. W pierwszym znaczeniu
używa się go jako określenie ogólnej cechy pomiarów i oznacza wątpliwość co do wartości wyniku
pomiaru. W drugim znaczeniu oznacza on ilościową miarę tej wątpliwości. W dalszej części tekstu
będziemy używać tego pojęcia w tym drugim znaczeniu. W Przewodniku niepewność pomiaru defi-
niowana jest następująco
6
:
Nie należy mylić pojęcia niepewności pomiarowej z pojęciem błędu pomiaru. Przypomnijmy, że przez
błąd pomiaru rozumiemy różnicę między wartością zmierzoną a rzeczywistą. Wartości błędu (na ogół)
nie znamy. Naszym zadaniem jest określenie stopnia wiarygodności naszego wyniku pomiaru, czyli
określenie
niepewności pomiaru
. Niepewność pomiaru określa szerokość przedziału, w którym mieści
się znaczna część wyników pomiaru (tych, które wykonaliśmy i ewentualnych przyszłych pomiarów
wykonanych tą samą metodą w tych samych warunkach), co pozwala nam wierzyć, że z dużym praw-
dopodobieństwem przedział ten zawiera również wartość rzeczywistą (oczywiście jeśli udało się nam
wyeliminować błędy systematyczne). Jednak sama szerokość tego przedziału nie może być interpre-
towana jako błąd pomiaru. Nawet w przypadku dużej niepewności pomiaru wartość zmierzona może
być bardzo bliska wartości rzeczywistej.
Określając niepewność pomiaru zakładamy, że pomiar jest wolny od nierozpoznanych oddziały-
wań systematycznych. Nierozpoznane oddziaływania systematyczne z natury rzeczy nie mogą być
uwzględnione przy szacowaniu niepewności pomiaru (patrz rys. 2.2 i opis do rysunku w tekście głów-
nym). Rozpoznane oddziaływania systematyczne możemy usunąć (jeśli jest to możliwe) lub skompen-
sować odpowiednią poprawką, a w ostateczności oszacować niepewność pomiaru wynikającą z tych
oddziaływań metodą B (patrz punkt 5.2).
3.1
Niepewność standardowa
Niepewność pomiarową podajemy w postaci tzw. odchylenia standardowego
7
i nazywamy
nie-
pewnością standardową
. Symbolem niepewności standardowej jest mała litera
8
. Wielkość, której
dotyczy niepewność standardowa podajemy w postaci symbolu lub opisu słownego w nawiasie za
literą , np.
,
,
poziom hemoglobiny we krwi . W przypadku, gdy rozkład statystyczny
zmiennej losowej jest tzw. rozkładem Gaussa, niepewność standardowa określa przedział, który
obejmuje ok. 68% wszystkich wyników pomiarów.
6
W dosłownym brzmieniu definicja niepewności w Przewodniku jest następująca: Niepewność pomiaru jest związanym z
rezultatem pomiaru parametrem, charakteryzującym rozrzut wyników, które można w uzasadniony sposób przypisać war-
tości mierzonej.
7
Odchylenia standardowe jest pojęciem statystycznym. Ogólnie mówiąc jest to miara rozrzutu statystycznego wartości
zmiennej losowej wokół jej wartości średniej.
8
Od angielskiego słowa uncertainty (niepewność).

Wprowadzenie do metod opracowywania danych pomiarowych
9
3.2
Niepewność rozszerzona
Szacując niepewność pomiaru wielkości
/ za pomocą niepewności standardowej / (lub
(
0
/ ) mamy ok. 68% pewności
9
, że rzeczywista wartość mierzonej wielkości mieści się w przedziale
1/2 − / , /2 + / 3. W niektórych zastosowaniach, gdy koszty popełnienia błędu są bardzo wyso-
kie np. wówczas, gdy chodzi o bezpieczeństwo lub zdrowie ludzi czy duże koszty finansowe, taki po-
ziom ufności może być za mały. W takiej sytuacji powinniśmy użyć takiej miary niepewności, która
wyznaczy nam przedział wokół wyniku pomiaru, po którym będziemy mogli oczekiwać, że zawiera się
w nim znacznie większa część rozkładu wartości wielkości mierzonej, a tym samym, że wartość rze-
czywista mieści się w nim z prawdopodobieństwem bliskim jedności. Taka miara niepewności jest
nazywana
niepewnością rozszerzoną
. Oznaczamy ją przez
4 i otrzymujemy mnożąc złożoną niepew-
ność standardową
0
przez tzw.
współczynnik rozszerzenia
5
4 / = 5
0
/ .
(3.1)
Ideałem byłoby móc wybrać wartość współczynnika rozszerzenia tak, aby przedział wyznaczony
na podstawie wartości zmierzonej i rozszerzonej niepewności pomiaru tej wartości odpowiadał ściśle
określonemu, wysokiemu poziomowi ufności, np. 95% lub 99%. W praktyce jest to jednak bardzo
trudne. Stosowane wartości współczynnika rozszerzenia k zawierają się zwykle w przedziale od 2 do
3, jednak w specjalnych zastosowaniach mogą być wybrane spoza tego przedziału. Taki wybór wynika
z własności rozkładu Gaussa, dla którego przedział ufności oparty na podwojonym odchyleniu stan-
dardowym ma poziom ufności równy ok. 95,5%, a oparty na potrojonym odchyleniu standardowym
ok. 99,7%. Przewodnik zaleca stosowanie wartości
5 = 2.
Dla rozkładu Gaussa poziom ufności odchylenia standardowego wynosi ok. 0,6827 (ok. 68,3%), po-
dwojonego odchylenia standardowego ok. 0,9545 (ok. 95,5%), a potrojonego odchylenia standardo-
wego ok. 0,9973 (ok. 99,7%). Zalecana przez przewodnik wartość współczynnika rozszerzenia
5 = 2
odpowiada poziomowi ufności na poziomie
95,5%.
Ponieważ poziom ufności niepewności rozszerzonej jest bardzo wysoki, możemy użyć jej do po-
równania wyniku pomiaru z wartością dokładną (wziętą z tablic lub wynikającą z teorii). Wnioskowa-
nie o zgodności wartości zmierzonej
/ z wartością dokładną / polega na obliczeniu różnicy / − / i
porównaniu jej z wartością niepewności rozszerzonej
4 / . Jeżeli |/ − / | < 4 / , to możemy uwa-
żać, że wartość zmierzona jest zgodna z wartością dokładną. W przeciwnym wypadku istnieje duże
prawdopodobieństwo, że popełniono jakieś błędy grube (pomyłki) lub pomiar zawiera jakiś błąd sys-
tematyczny pochodzący od nierozpoznanego czynnika.
4.
Pomiary bezpośrednie i pośrednie
Pomiary możemy podzielić na
bezpośrednie
i
pośrednie
. Wykonując pomiar bezpośredni porów-
nujemy mierzoną wielkość wprost z jej miarą wzorcową (jednostką) zrealizowaną za pomocą przyrzą-
du pomiarowego (mówiąc prościej odczytujemy wartość mierzoną wprost z przyrządu pomiarowe-
go). Przykładem może być pomiar szerokości kartki papieru za pomocą miarki milimetrowej (linijki),
pomiar czasu trwania jakiegoś zjawiska za pomocą stopera lub pomiar napięcia elektrycznego za po-
mocą woltomierza.
9
Takie prawdopodobieństwo odpowiada sytuacji, gdy zmienna losowa podlega rozkładowi Gaussa. w przypad-
ku rozkładu prostokątnego wynosi ono ok. 58%, a w przypadku trójkątnego ok. 70%.

Obliczanie i wyrażanie niepewności pomiarowych
10
W pomiarze pośrednim wykonujemy pomiary (bezpośrednie lub pośrednie) innych wielkości fi-
zycznych, takich, które wiążą się z naszą wielkością fizyczną znaną nam zależnością funkcyjną. Przy-
kładem może być pomiar objętości V kuli poprzez pomiar (bezpośredni) jej średnicy d i skorzystanie
ze wzoru na objętość kuli:
< =
=>
?
@
, czy pomiar wartości przyśpieszenia ziemskiego g poprzez pomiar
długości l tzw. wahadła prostego oraz jego okresu T, a następnie skorzystanie ze wzoru (w tym przy-
padku przybliżonego) na okres drgań harmonicznych tego wahadła
= 2AB
C
D
, skąd dostajemy:
E =
F=
G
C
G
.
5.
Ocena niepewności standardowej pomiaru bezpośrednie-
go
Definicja niepewności pomiaru sugeruje różne sposoby określania niepewności pomiaru. Prze-
wodnik zaleca używanie jako miary niepewności pomiaru tzw.
niepewności standardowej
, a w szcze-
gólnych przypadkach tzw.
niepewności rozszerzonej
. Przewodnik opisuje dwie metody szacowania
niepewności standardowej: metodę A i metodę B. Nie należy kojarzyć tych metod z podziałem błę-
dów pomiaru na błędy przypadkowe i systematyczne, gdyż podział na te dwie metody nie wynika z
natury składników niepewności, lecz jedynie sposobów szacowania niepewności standardowej.
5.1
Ocena niepewności standardowej metodą A
Metoda typu A wykorzystuje statystyczną analizę serii wyników pomiaru. Seria pomiarów
powinna być wykonana w warunkach powtarzalności. Czyli m.in. tą samą metodą pomiarową, przez
tego samego obserwatora, tym samym przyrządem, w krótkich odstępach czasu. W takich warun-
kach, najlepszym oszacowaniem (estymatą) wartości mierzonej wielkości , dla której wykonano n
niezależnych pomiarów, jest średnia arytmetyczna
̅ z I pomiarów
̅ ≡
1
I K
L
M
LNO
.
5.1
W większości przypadków statystyczny rozrzut wyników pomiarów jest opisywany przez tzw. rozkład
Gaussa, zwany też rozkładem normalnym. Nie wnikając w szczegóły i ścisłą definicję przyjmijmy, że
rozkład prawdopodobieństwa
(
rozkład gęstości prawdopodobieństwa
) jest funkcją określającą praw-
dopodobieństwo, że
zmienna losowa
przyjmuje wartość należącą do danego zbioru wartości. Rozkład
Gaussa dany jest funkcją
P( ) =
1
Q√2A
S
T(UTV)
G
WX
G
.
(5.2)
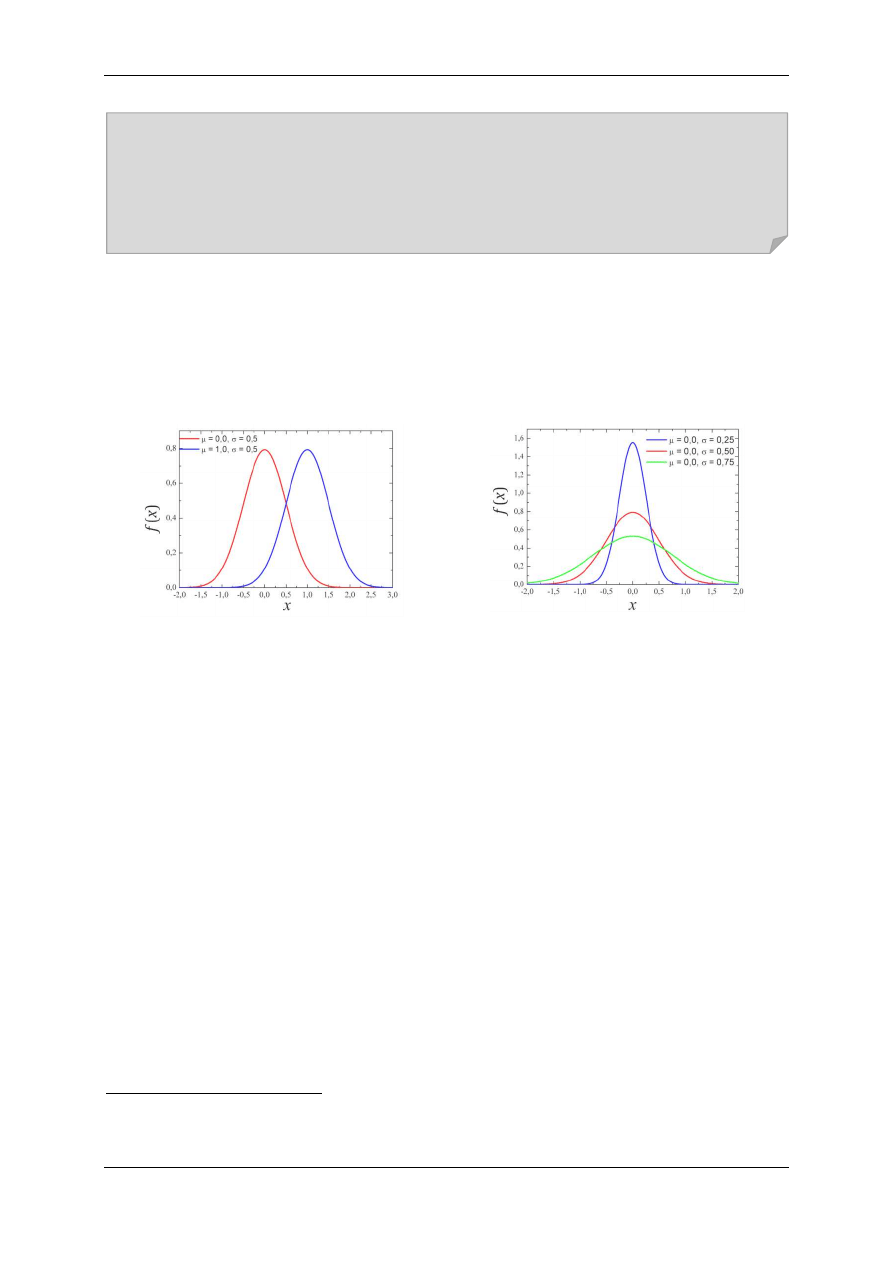
Krzywa rozkładu Gaussa przypomina dzwon w przekroju poprzecznym i dlatego często nazywana jest
krzywą dzwonową. Jej kształt i położenie zależy od parametrów
Y i Q. Rozkład Gaussa jest symetrycz-
ny względem
= Y i w punkcie tym osiąga wartość maksymalną. Przybliżoną wartością (estymatą)
tego parametru, wyznaczoną na podstawie skończonej serii pomiarowej jest wspominana wyżej
średnia arytmetyczna serii
I wyników pomiaru. Drugi z parametrów rozkładu Gaussa Q nazywany jest
odchyleniem standardowym
.
Wprowadzenie do metod opracowywania danych pomiarowych
11
W ogólności odchylenie standardowe jest dodatnim pierwiastkiem
wariancji
. Wariancja jest jed-
nym z najważniejszych parametrów stosowanych do opisu rozkładów statystycznych (nie tylko
rozkładu Gaussa). Wariancja jest miarą rozproszenia wartości zmiennej losowej wokół jej wartości
średniej i definiowana jest jako wartość oczekiwana (wartość średnia) kwadratów różnic poszcze-
gólnych wartości zmiennej i ich wartości oczekiwanej (wartości średniej).
Odchylenie standardowe decyduje o „szerokości” krzywej Gaussa
10
. Czym mniejszy jest parametr
Q,
tym „węższa” jest krzywa Gaussa (patrz Rys. 4.1 b). To z kolei decyduje o wielkości rozrzutu wyników
pomiaru. Wyniki pomiarów podlegające rozkładowi Gaussa o małej wartości parametru
Q będzie
cechować mniejszy rozrzut niż wyniki pomiarów podlegające rozkładowi Gaussa o dużej wartości
parametru
Q. Dlatego parametr Q możemy w naturalny sposób przyjąć za
miarę niepewności pomia-
ru
.
(a)
(b)
Rys. 5.1. Przykładowe krzywe Gaussa a) różniące się parametrami
Y, b) różniące się parametrami Q.
Pole pod krzywą rozkładu gęstości prawdopodobieństwa zmiennej losowej w danym przedziale jest
równe prawdopodobieństwu wystąpienia wartości zmiennej losowej w tym przedziale. Oczywiście
pole pod całą krzywą Gaussa, czyli pole w przedziale
−∞, ∞ jest równe jedności, gdyż jest zdarze-
niem pewnym, ze wartość zmiennej losowej przyjmie dowolną wartość z przedziału
−∞, ∞ . Pole
pod krzywą Gaussa w przedziale
[Y − Q, Y + Q] wynosi ok. 0,683. Można stąd wnioskować, że staty-
stycznie ok.
0,683 ∙ I spośród I wyników serii pomiarów będzie skupiona w przedziale [Y − Q, Y +
Q], zaś ok. 0,317 ∙ I wyników pomiarów ułoży się poza tym przedziałem, przy czym mniej więcej po-
łowa z nich po lewej stronie tego przedziału, a połowa po prawej jego stronie.
Podobnie jak w przypadku parametru
Y, na podstawie skończonej liczby obserwacji możemy
jedynie oszacować wartość parametru
Q. Estymata (oszacowanie) wartości odchylenia standardowe-
go
Q zmiennej , otrzymane na podstawie serii I wyników pomiaru nazywana jest
odchyleniem stan-
dardowym eksperymentalnym
i oznaczana symbolem
b
U
lub
b . Estymatę odchylenia standardo-
wego wyliczamy ze wzoru
10
Szerokość krzywej Gaussa należy rozumieć w sensie umownym. Krzywa Gaussa jest nieskończenie szeroka,
gdyż asymptotycznie dąży do wartości zerowej przy
→ −∞ i → ∞. Jednak w zależności od wartości parame-
tru
Q, przedział, w którym wartości funkcji Gaussa są wyraźnie niezerowe może być większy lub mniejszy.
Obliczanie i wyrażanie niepewności pomiarowych
12
b
U
= b
= d
1
I − 1 K
L
− ̅
W
M
LNO
.
5.3
Wartość
b
U
możemy uważać za miarę niepewności pomiaru, w przypadku, gdy za wynik pomiaru
przyjęlibyśmy którąkolwiek z wartości
L
naszej serii pomiarowej. Dlatego
b
U
nazywa się czasem od-
chyleniem standardowym pojedynczego pomiaru. Jednak dla nas bardziej interesująca jest wartość
niepewności, z jaką szacujemy wartość wielkości mierzonej za pomocą średniej arytmetycznej serii
wyników pomiaru. Średnia arytmetyczna
̅ jest, podobnie jak zmienna , zmienną losową i jeśli
zmienna podlega rozkładowi Gaussa, to również
̅ podlega rozkładowi Gaussa. Można pokazać, że
estymata odchylenia standardowego średniej arytmetycznej
s
f2
jest
√I razy mniejszy od estymaty
odchylenia standardowego
b
U
, gdzie
I jest liczbą pomiarów, na podstawie której wyliczono średnią
arytmetyczną
̅
b
U̅
= b( ̅) =
b
U
√I
.
(5.4)
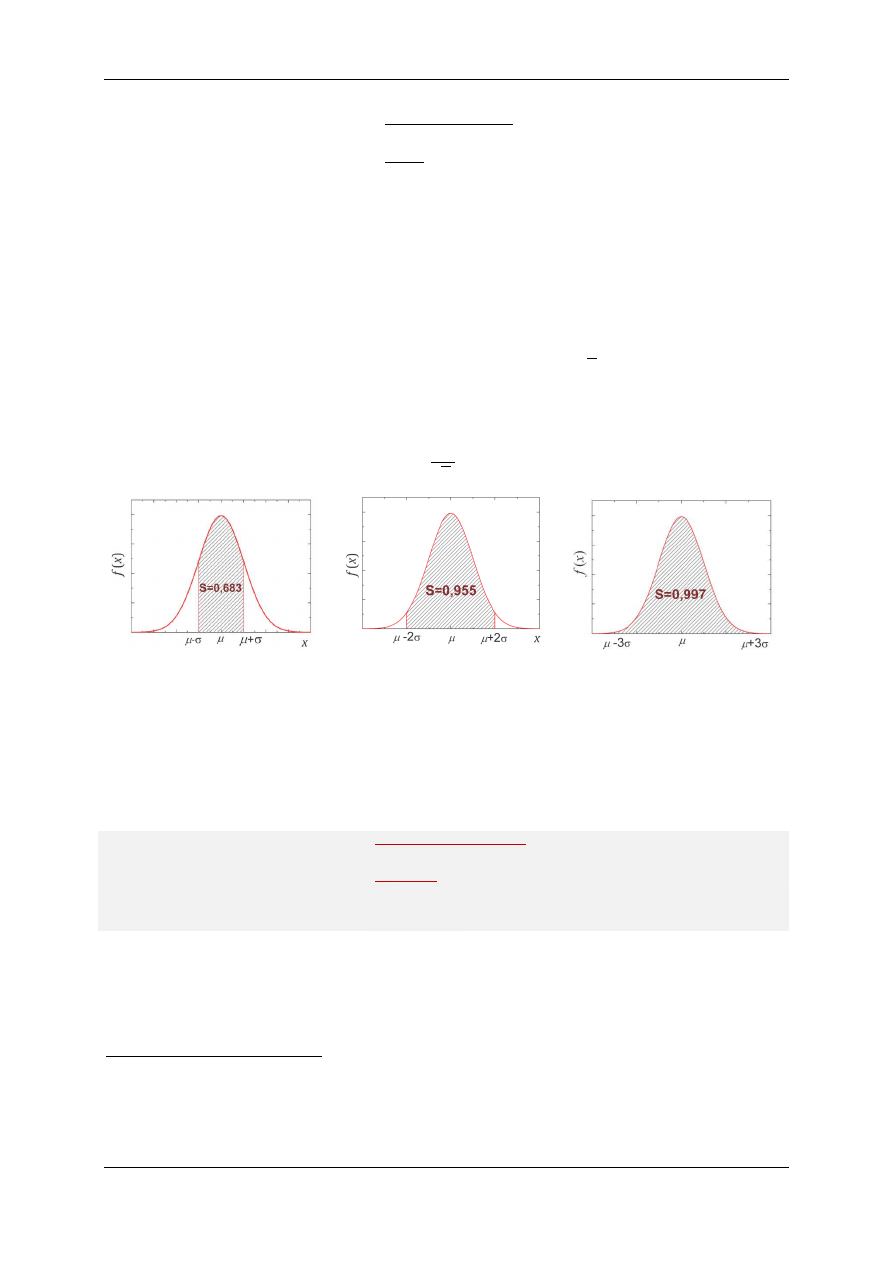
(a)
(b)
(c)
Rys. 5.2. Pole powierzchni pod krzywą Gaussa dla przedziałów:
[Y − Q, Y + Q\ (a), [Y − 2Q, Y +
2Q\ (b) i [Y − 3Q, Y + 3Q\ (c). Każde z tych pól odpowiadają prawdopodobieństwu wystąpienia
wartości w odpowiednim przedziale.
Ponieważ jako wynik pomiaru przyjmujemy średnią arytmetyczną
̅ serii I wyników pomiarów, es-
tymata odchylenia standardowego średniej arytmetycznej
b
U̅
jest miarą niepewności pomiaru. Tak
określoną niepewność pomiaru nazywamy
niepewnością standardową
i oznaczamy symbolem
( )
11
( ) = b
U̅
= d
1
I(I − 1) K(
L
− ̅)
W
M
LNO
.
(5.5)
Oczywiście niepewność pomiaru ma wymiar wielkości mierzonej. Niepewność tę nazywamy również
niepewnością bezwzględną. Inną, wygodną miarą niepewności jest
niepewność standardowa względ-
na
, którą definiujemy jako stosunek niepewności standardowej (bezwzględnej) do wartości zmierzo-
nej
11
Oznaczenie niepewności standardowej
( ), podobnie jak wcześniej podane oznaczenia estymat odchylenia
standardowego
b( ) i odchylenia standardowego średniej arytmetycznej b( ̅) może być mylące, ponieważ
przypominają one symbole funkcji. Musimy pamiętać, że
( ), b( ), b( ̅) są liczbami, a nie funkcjami zmien-
nej , czy zmiennej
̅. Przewodnik wprowadza tego typu oznaczenie, gdyż jest ono wygodniejsze i czytelniejsze
w wypadku zmiennych, które wygodniej jest opisywać słownie, np.
(poziom cukru we krwi).

Wprowadzenie do metod opracowywania danych pomiarowych
13
j
≡
.
5.6
Niepewność względna jest wielkością bezwymiarową, często podawaną w procentach (po wymnoże-
niu wyrażenia
(5.6) przez 100). Dzięki niepewności względnej możemy porównywać niepewności
wielkości fizycznych mających różne wymiary.
Biorąc pod uwagę opisane wcześniej własności odchylenia standardowego, wynikowi pomia-
ru określonemu poprzez wyznaczenie średniej arytmetycznej
̅ serii I wyników pomiaru oraz nie-
pewność pomiaru wyznaczoną jako niepewność standardową
( ), możemy nadać następującą in-
terpretację:
Wartość wielkości mierzonej mieści się w przedziale
( ̅ − ( ), ̅ + ( )) z prawdopodobień-
stwem ok. 0,683
Oczywiście powyższe zdanie jest prawdziwe pod pewnymi warunkami. Po pierwsze wielkość losowa
podlega rozkładowi Gaussa, po drugie liczba pomiarów była wystarczająco duża i po trzecie udało
nam się wyeliminować lub skompensować wszystkie błędy systematyczne.
Należy podkreślić statystyczny charakter tak określonego wyniku pomiaru. Dla przykładu, gdyby wy-
konać w warunkach powtarzalności 100 serii pomiarowych, to okaże się, że statystycznie w ok. 68.
przypadkach przedziały
( ̅ − ( ), ̅ + ( )) będą zawierać rzeczywistą wartość wielkości mierzonej,
a w ok. 32 przypadkach wartość rzeczywista będzie znajdować się poza wyznaczonym przedziałem,
mimo tego, ze każda seria pomiarów była wykonana w jednakowych warunkach, jednakową metodą i
jednakowo starannie.
Wyznaczony przez wynik pomiaru i jego niepewność przedział nazywamy
przedziałem ufności
lub
przedziałem objęcia
, a prawdopodobieństwo tego, że w przedziale tym mieści się wartość wielko-
ści mierzonej nazywamy
poziomem ufności
lub
poziomem objęcia
12
. Poziom ufności przedziału dla
którego szerokość wyznaczyliśmy na podstawie niepewności standardowej wynosi ok. 0,683 (w przy-
padku rozkładu Gaussa, dla innych rozkładów poziom ufności jest nieco inny (patrz następny roz-
dział)).
Podkreślmy jeszcze, że zdefiniowana powyżej wielkość
b
U̅
jest tylko estymatą (oszacowaniem)
wartości odchylenia standardowego średniej arytmetycznej. To oszacowanie jest tym lepsze im więk-
sza jest liczba pomiarów, więc liczba pomiarów powinna być duża. Z drugiej strony dokładność osza-
cowania rośnie dość wolno ze wzrostem liczby pomiarów (w przybliżeniu jak
k2(I − 1) ), więc wy-
konywanie dużych serii pomiarowych jest nieopłacalne. Przyjmuje się, że liczba pomiarów powinna
wynosić co najmniej
5 ÷ 10. Przy mniejszej liczbie pomiarów za wynik pomiaru również przyjmujemy
średnią arytmetyczną, ale niepewność pomiaru należy wyznaczyć metodą B (patrz następny podroz-
dział).
Przykład 1.
Za pomocą stopera elektronicznego wykonano 10 pomiarów czasu trwania 10 okresów waha-
dła fizycznego. Otrzymane wyniki pomiarów zebrano w poniższej tabeli:
12
Druga z tych nazw podkreśla inną interpretację tego parametru, a mianowicie to, że szacuje on, jaka część
rozkładu, czy w przypadku serii pomiarowej, jaka część wyników serii pomiarowej mieści się statystycznie w
przedziale objęcia (przedziale ufności).
Obliczanie i wyrażanie niepewności pomiarowych
14
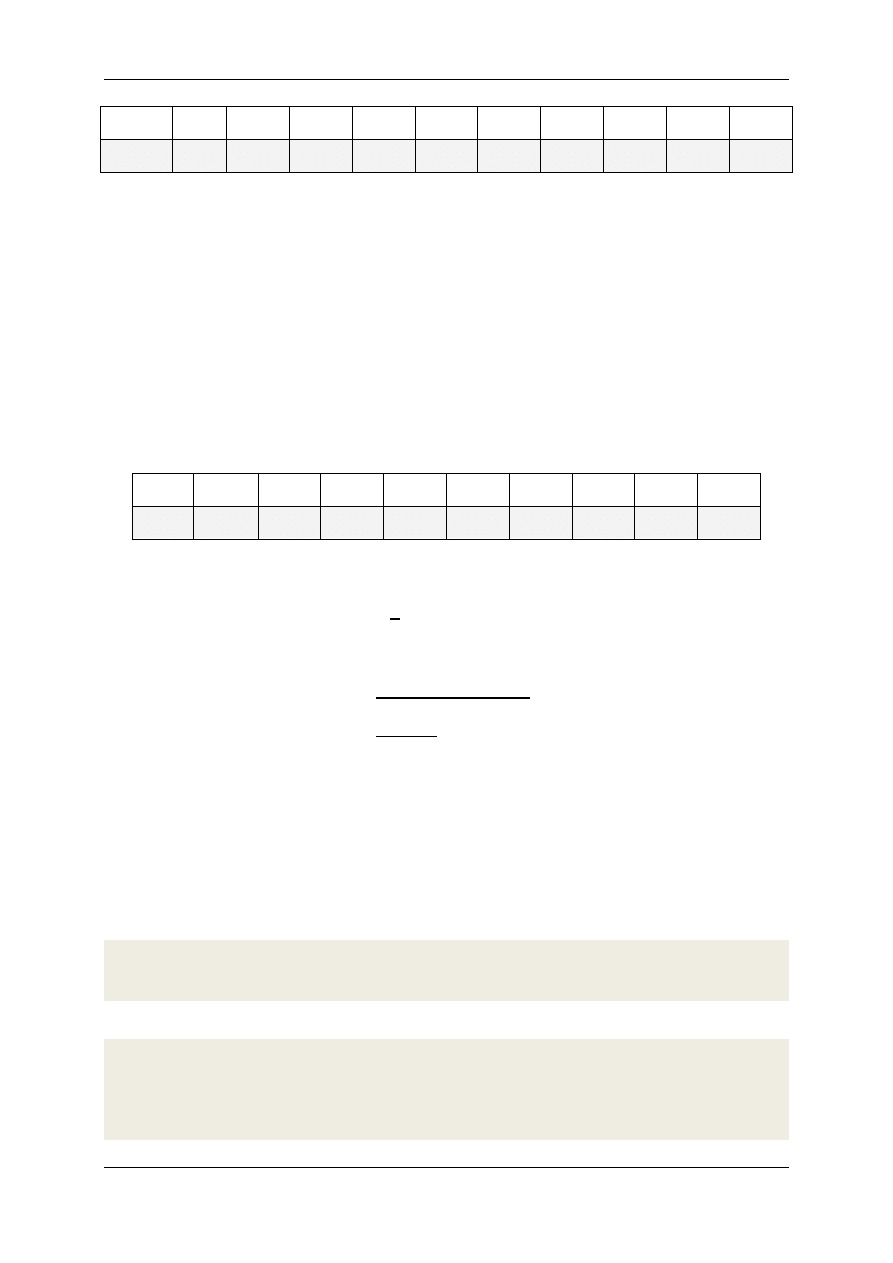
l.p.
1
2
3
4
5
6
7
8
9
10
10T [s]
14,55
14,50
14,40
14,48
14,62
14,50
16,02
14,52
14,57
14,60
Przyglądając się poszczególnym wynikom pomiarów zauważamy, że 7. wynik zdecydowanie
odbiega od pozostałych. Jest od nich o ok. 1,5 s większy, co jest wartością zbliżoną do jednego
okresu. Można podejrzewać, że obserwator pomylił się i zmierzył czas 11. zamiast 10. okresów.
Jest to przykład błędu grubego. Taki wynik pomiaru należy odrzucić (lub zastąpić go dodatko-
wym poprawnie wykonanym pomiarem). Do dalszej analizy weźmiemy zatem wyniki 9. pomia-
rów. Zwróćmy uwagę na zapis wyników pomiaru o numerach 2, 3, 6, 10 w powyższej tabelce.
Przykładowo wynik pomiaru 2. został zapisany jako
14.50 s, a nie 14.5 s. Podkreśla to fakt, że
użyty do pomiaru przyrząd pomiarowy, jakim w tym wypadku jest stoper elektroniczny, umoż-
liwia nam odczyt czasu z dokładnością do
0,01 s.
Po podzieleniu wartości pomiarów przez 10 otrzymujemy pomiary czasu pojedynczego okresu
drgań wahadła:
l.p.
1
2
3
4
5
6
7
8
9
T [s]
1,455
1,450
1,440
1,448
1,462
1,450
1,452
1,457
1,460
Średnia arytmetyczna wyników tych pomiarów wynosi
2 = 1
9 K
L
m
LNO
≈ 1,45633 s,
zaś niepewność standardowa liczona z wzoru dla estymaty odchylenia standardowego średniej
arytmetycznej wynosi
= b
2
= d
1
9 9 − 1 K
L
− 2
W
m
LNO
≈ 0,02242 s.
Otrzymane w wyniku obliczeń liczby należy odpowiednio zaokrąglić, a następnie zapisać wynik
pomiaru. Reguły zaokrąglania i zapisu wyników pomiaru podamy w rozdziale 7. Tu ograniczymy
się jedynie do zapisu wyniku pomiaru w trzech zalecanych przez Przewodnik postaciach:
a)
Okres drgań wahadła wynosi
1,456 s z niepewnością 0,022 s.
b)
= 1,456 s;
= 0,022 s.
c)
= 1,456 22 s.
Uwaga
►
Zaprezentowane powyżej postaci zapisów pomiaru stosujemy wówczas, gdy miarą nie-
pewności pomiaru jest niepewność standardowa. Jeśli jako miarę niepewności zastosujemy niepew-
ność rozszerzoną (będziemy o niej mówić nieco później), to zapis wyniku pomiaru będzie nieco inny.
Do wyliczenia wartości średniej arytmetycznej oraz estymaty wartości odchylenia standardowego
średniej arytmetycznej można skorzystać z programu MS Excel. Średnią arytmetyczną liczb wyliczymy
za pomocą funkcji Excela o nazwie ŚREDNIA. Jeśli np. wyniki pomiaru wpiszemy do komórek A1:A10,
to formuła =ŚREDNIA(A1:A10) wyliczy nam średnią arytmetyczną liczb z komórek A1:A10. Excel udo-
stępnia nam również funkcję o nazwie ODCH.STANDARDOWE. Musimy jednak pamiętać, że funkcja ta

Wprowadzenie do metod opracowywania danych pomiarowych
15
wylicza estymatę wartości odchylenia standardowego, a nie odchylenia standardowego średniej
arytmetycznej. Dlatego wynik działania tej funkcji musimy jeszcze podzielić przez pierwiastek z liczby
pomiarów. Pierwiastek liczby możemy w Excelu wyliczyć za pomocą funkcji PIERWIASTEK lub wyko-
nując operację potęgowania z wykładnikiem 0,5 (operatorem potęgowania w Excelu jest znak ^, np.
formuła
= 10^0,5 wyliczy nam potęgę 10
,p
= √5).
Przykładowa formuła znajdująca estymatę wartości odchylenia standardowego średniej arytmetycz-
nej 10. liczb wpisanych do komórek A1:A10 może zatem wyglądać tak:
=ODCH.STANDARDOWE(A1:A10)/PIERWIASTEK(10).
Uwaga: W Excelu w wersji MS Office 2010 zmieniono nazwę tej funkcji na ODCH.STAND.POPUL
5.2
Ocena niepewności standardowej metodą B
Metodę B oceny niepewności standardowej stosujemy wówczas, gdy zastosowanie metody A
opartej na analizie statystycznej nie jest możliwe, np. wówczas, gdy
•
Dysponujemy zbyt małą liczbą wyników pomiarów (w szczególnym przypadku tylko jednym).
•
Wyniki pomiarów nie wykazują rozrzutu (taka sytuacja ma miejsce wówczas, gdy wpływ
czynników losowych na wyniki pomiaru jest dużo mniejszy od dokładności użytego przyrządu
pomiarowego).
•
Na pomiar wpływają rozpoznane czynniki systematyczne, których jednak nie potrafimy ani
wyeliminować, ani skompensować odpowiednią poprawką.
Metoda typu B wymaga od eksperymentatora doświadczenia i ogólnej wiedzy. Jak podaje Przewod-
nik: „Jest to umiejętność zawodowa, którą można nabyć wraz z praktyką”. Metoda B określa niepew-
ność standardową na drodze analizy naukowej wykorzystującej wszystkie dostępne informacje o
możliwej zmienności wartości mierzonej wielkości. Przewodnik podaje następujący zestaw takich
informacji:
•
Poprzednie dane pomiarowe;
•
Posiadane doświadczenie wraz z ogólną znajomością zjawisk i właściwości odpowiednich ma-
teriałów odniesienia i przyrządów;
•
Specyfikacje wytwórców;
•
Dane uzyskane z wzorcowania i certyfikacji;
•
Niepewności przypisane danym odniesienia zaczerpniętym z podręczników.
Ocena niepewności metodą B najczęściej będzie dotyczyła określenia niepewności związanej ze skoń-
czoną dokładnością przyrządów pomiarowych. Sposób oceny tej niepewności będzie zależeć od typu
przyrządu.
5.2.1
Przedział graniczny
W dalszych rozważaniach przyda się nam pojęcie
przedziału granicznego
. Jest to przedział, w któ-
rym (według naszej wiedzy) mieszczą się wszystkie wyniki pomiarów zarówno te aktualnie wykonane
jak i przyszłe. Załóżmy, że udało nam się oszacować górną i dolną granicę
q
i
T
mierzonej wielkości
. Oznacza to, że prawdopodobieństwo wystąpienia wyniku pomiaru leżącego w przedziale (granicz-
nym)
T
,
q
wynosi jeden, a prawdopodobieństwo wyniku pomiaru leżącego poza tym przedziałem
jest zerowe. Ponieważ Przewodnik zaleca stosować niepewność standardową jako miarę niepewno-
ści, to powinniśmy obliczyć odchylenie standardowe rozkładu naszej zmiennej na przedziale granicz-
Obliczanie i wyrażanie niepewności pomiarowych
16
nym. Jeśli mamy informacje na temat kształtu tego rozkładu, to powinniśmy je wykorzystać. Jednak
na ogół nasza wiedza nt. rozkładu prawdopodobieństwa wyników pomiaru jest za mała i musimy
założyć jakiś prosty rozkład zgodny z naszym doświadczeniem. Najczęściej będzie to
rozkład prosto-
kątny
lub
rozkład trójkątny
.
Rozkład prostokątny
Jeśli nie mamy żadnych szczegółowych informacji na temat rozkładu prawdopodobieństwa war-
tości naszej zmiennej wewnątrz przedziału granicznego, możemy przyjąć tzw. rozkład prostokątny
13
.
Zakładamy tym samym, że gęstość prawdopodobieństwa wystąpienia dowolnej wartości mieszczącej
się w tym przedziale jest stała. W takim przypadku, korzystając z własności rozkładu prostokątnego,
możemy pokazać, że wartością oczekiwaną naszej zmiennej, którą przyjmiemy za wartość zmierzoną
będzie punkt środkowy przedziału granicznego
=
q
+
T
2
,
5.7
zaś odchylenie standardowe, które będzie naszą niepewnością standardową pomiaru wynosi
( ) = r
(
q
−
T
)
W
12
.
(5.8)
Jeśli szerokość
(
q
−
T
) przedziału oznaczymy przez 2Δ , to niepewność standardowa przyjmie
prostszą postać
( ) =
Δ
√3
.
(5.9)
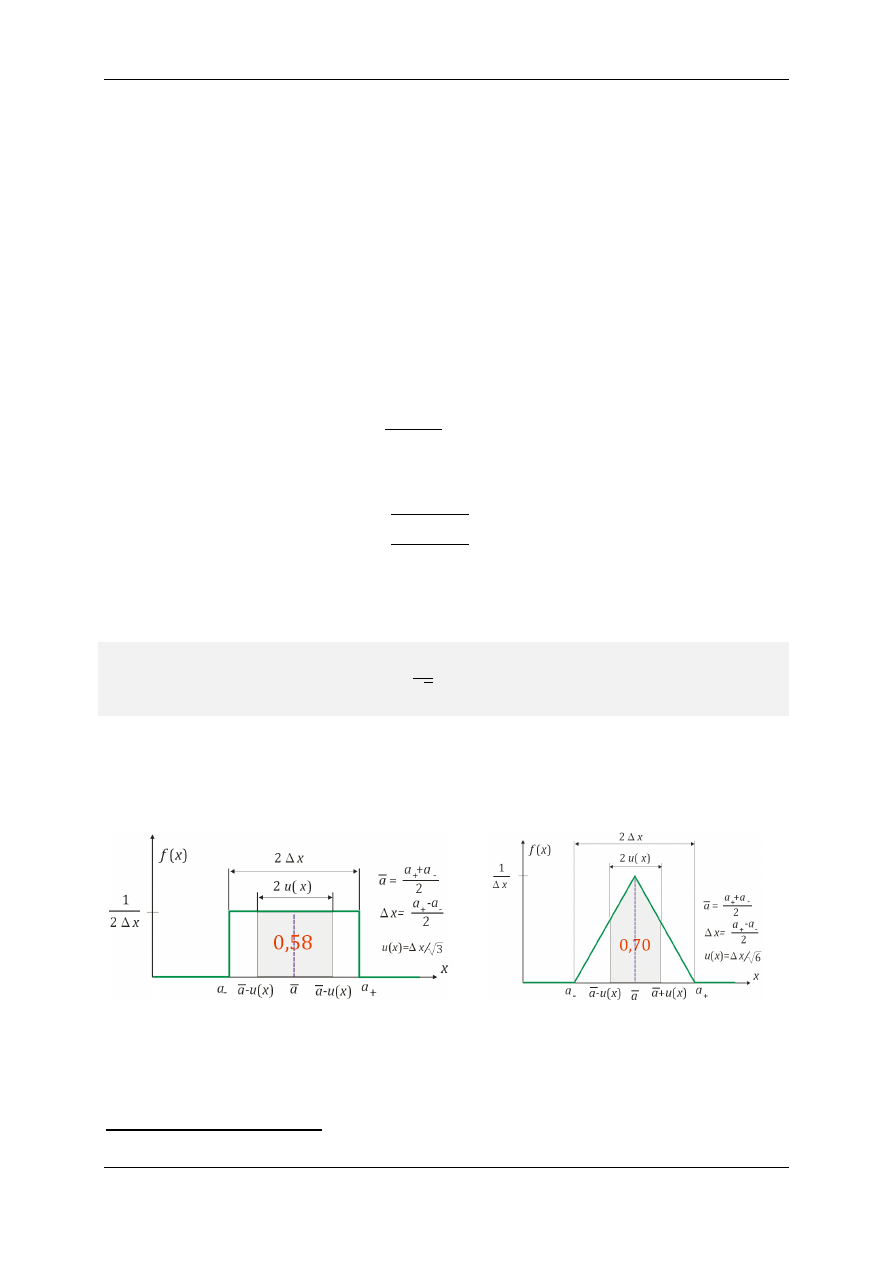
Wykres rozkładu prostokątnego przedstawia Rysunek 4.3 (a). Zacieniowany obszar pod wykresem
odpowiada przedziałowi objęcia określonego przez odchylenie standardowe rozkładu prostokątnego
(wzór
(5.9)). Zajmuje on ok. 57,7% całej powierzchni pod wykresem, co oznacza, ze poziom ufności
(poziom objęcia) rozkładu prostokątnego wynosi ok.
57,7%. Przypomnijmy, że dla rozkładu Gaussa
wynosi on ok.
68,3% .
(a)
(b)
Rys. 4.3. Prostokątny (a) i trójkątny (b) rozkład gęstości prawdopodobieństwa.
13
Rozkład prostokątny nazywany jest również rozkładem jednostajnym lub równomiernym.

Wprowadzenie do metod opracowywania danych pomiarowych
17
0
cm
0
0
10
20
10
20
20
10
cm
5
15
5
15
(a)
(b)
(c)
cm
Rys. 4.4. Odczyt długości pręta za
pomocą przymiarów o trzech różnych
skalach
Rozkład trójkątny
W wielu przypadkach rozkład prostokątny jest mało realistyczny. Spodziewamy się, że wystąpie-
nie wartości ze środka przedziału jest bardziej prawdopodobne niż wystąpienie wartości znajdujących
się w pobliżu jego granic. Jeśli potrafimy określić szczegółów tego rozkładu, to przyjmujemy trójkątny
rozkład prawdopodobieństwa (patrz Rysunek 4.3 (b)). Dla trójkątnego rozkładu prawdopodobieństwa
o szerokości
2Δ , odchylenie standardowe wynosi
=
Δ
√6
.
5.10
Poziom objęcia (poziom ufności) odchylenia standardowego dla rozkładu trójkątnego jest podobny
do poziomu objęcia dla rozkładu Gaussa i wynosi ok.
70,0% .
5.2.2
Proste przyrządy mechaniczne
Do przyrządów wymienionych w tytule możemy zaliczyć takie przyrządy pomiarowe jak
przymiar milimetrowy, suwmiarka, śruba mikrometryczna, termometry cieczowe itp. Przyrządy te nie
mają na ogół określonych przez producenta dokładności. Za uzasadnione przyjmuje się powszechne
przekonanie, że dokładność tych przyrządów ma związek z wartością najmniejszej działki przyrządu,
tzw.
działki elementarnej
. Odczyt wartości wielkości mierzonej z tego typu przyrządu z dokładnością
większą niż działka elementarna wymaga wprawy i pewnych zdolności percepcyjnych. W zależności
od umiejętności osoby wykonującej pomiar, a także od odległości pomiędzy najbliższymi kreskami
skali możliwy jest pomiar z różną niepewnością (patrz Przykład 1).
Przykład 1
Rozważmy sytuację przedstawioną na Rys. 4.4. Pokazano
tam pomiary długości pręta wykonane przymiarami o trzech
różnych skalach.
a)
W przypadku (a) działka elementarna skali przymiaru
ma długość
5 cm. O odczytanej wartości długości pręta mo-
żemy powiedzieć, że mieści się pomiędzy
15 cm a 20 cm, ale
jest wyraźnie bliższa wartości
20 cm niż 15 cm. Precyzyjniej-
sze odczytanie tej wartości wymaga pewnej wprawy i zdol-
ności. Odczyt wykonany przez różne osoby może się różnić.
Osoba wykonująca pomiar musi określić niepewność pomia-
ru, jaka wynika z subiektywności jej oceny części działki ele-
mentarnej zajmowanej przez mierzony pręt. W tym celu
możemy oszacować krańce przedziału granicznego, a następnie obliczyć niepewność standardową
korzystając z rozkładu trójkątnego, który w tym przypadku jest bardziej realistyczny niż rozkład pro-
stokątny. Dla osoby mającej wprawę w odczytach z tego typu przyrządu (o tak szerokiej działce ele-
mentarnej) nie powinno stanowić problemu ocena położenia na skali z dokładnością do
1 5
⁄ działki
elementarnej. W przypadku a) osoba taka mogłaby odczytać długość pręta np. tak:
= 15 cm +
t
p
∙
5 cm = 18 cm i ustalić krańce przedziału granicznego
T
= 18 cm −
O
p
∙ 5 cm = 17 cm oraz
q
= 18 cm +
O
p
∙ 5 cm = 19 cm. Połowa szerokości przedziału granicznego wynosi Δ = 1 cm. Nie-
pewność standardową tego pomiaru wyliczymy ze wzoru
5.10

Obliczanie i wyrażanie niepewności pomiarowych
18
=
1 cm
√6
≈ 0,4082 cm ≈ 0,41 cm.
Wynik tego pomiaru zapisalibyśmy w jednej z poniższych postaci:
•
Długość pręta wynosi
18,00 cm z niepewnością 0,41 m.
•
= 18,00 cm;
= 0,41 cm.
•
= 18,00 41 cm.
Oczywiście osoba mniej wprawna mogłaby dokonać odczytu z dokładnością np. do
1 3
⁄ działki ele-
mentarnej i dokonać następującej oceny:
= 15 cm +
W
t
∙ 5 cm ≈ 18,333 cm; krańce przedziału gra-
nicznego
T
= 18,333 cm −
O
t
∙ 5 cm = 16,667 cm oraz
q
= 18 cm +
O
t
∙ 5 cm = 20,00 cm. Szero-
kość przedziału granicznego wynosi teraz
Δ ≈ 1,667 cm. Niepewność standardowa jest w tym wy-
padku równa
=
1,667 cm
√6
≈ 0,680 cm.
Ostatecznie wynik pomiaru możemy zapisać tak:
•
Długość pręta wynosi
18,33 cm z niepewnością 0,68 m.
•
= 18,33 cm;
= 0,68 cm.
•
= 18,33 68 cm.
Zauważmy, że pomiary wykonane przez obie osoby są zgodne, gdyż ich przedziały objęcia (i to już na
poziomie niepewności standardowej) zazębiają się, co pokazuje Rys 4.5.
b)
W przypadku z rysunku b) wynik pomiaru mógłby być np. taki:
= 18 cm +
O
p
∙ 2 cm =
18,4 cm. Krańcami przedziału granicznego są
T
= 18,4 cm −
O
p
∙ 2 cm = 18,0 cm oraz
q
=
18,4 cm +
O
p
∙ 2 cm = 18,8 cm. Połowa szerokości przedziału granicznego wynosi teraz Δ ≈ 0,4 cm.
Niepewność standardowa jest w tym wypadku równa
=
0,4 cm
√6
≈ 0,163 cm.
Ostatecznie wynik pomiaru możemy zapisać tak:
•
Długość pręta wynosi
18,40 cm z niepewnością 0,16 m.
•
= 18,40 cm;
= 0,16 cm.
•
= 18,40 16 cm.
c)
W trzecim z omawianych przypadków działka elementarna jest najmniejsza. Załóżmy, że ob-
serwator może tego dokonać odczytu z dokładnością do
1 4
⁄ działki elementarnej
14
. Wynik pomiaru
mógłby być np. taki:
= 18 cm +
W
F
∙ 1 cm = 18,5 cm. Krańcami przedziału granicznego są
T
= 18,5 cm −
O
F
∙ 1 cm = 18,25 cm oraz
q
= 18,5 cm +
O
F
∙ 1 cm = 18,75 cm. Połowa szerokości
przedziału granicznego wynosi teraz
Δ ≈ 0,25 cm. Niepewność standardowa jest w tym wypadku
równa
14
Czym mniejsza jest działka tym trudniej dokonać odczytu z dokładnością do małego ułamka wartość działki.
W skrajnej sytuacji ograniczamy się do oceny odczytu z dokładnością do
1/2, a nawet do jednej działki elemen-
tarnej.

Wprowadzenie do metod opracowywania danych pomiarowych
19
=
0,25 cm
√6
≈ 0,102 cm.
Ostatecznie wynik pomiaru możemy zapisać tak:
•
Długość pręta wynosi
18,50 cm z niepewnością 0,10 m.
•
= 18,50 cm;
= 0,10 cm.
•
= 18,50 10 cm.
Wszystkie wyniki pomiarów omówione powyżej są ze sobą zgodne, gdyż przedziały przez nie wyzna-
czone zazębiają się. Jak można się było spodziewać największą niepewność dostaliśmy mierząc dłu-
gość pręta przymiarem a), a najmniejszą przymiarem c) o najmniejszej działce elementarnej
18,0 cm
18,5 cm
19,0 cm
18,00(41) cm
18,33(68) cm
17,5 cm
18,40(16) cm
18,50(10) cm
Rys. 4.5. Porównanie wyników pomiaru długości pręta omówionych w Przykładzie 1. Dwa prze-
działy niebieski odpowiadają pomiarom wykonanych przez dwie różne osoby przymiarem a).
Przedział zielony odpowiada pomiarowi przymiarem b), a przedział czerwony przymiarem c).
Zwróćmy uwagę na pomiary wykonane przez różne osoby przymiarem a). Pierwsza z tych osób
otrzymała wynik
= 18,00 41 cm, a druga = 18,33 68 cm. Niepewność pomiaru wykonanego
przez drugą osobę jest większa niż niepewność pomiaru pierwszej. Nie musi to jednak oznaczać, że
błąd pomiaru wykonanego przez druga osobę jest większy niż w przypadku pomiaru wykonanego
przez osobę pierwszą! Patrząc na wyniki pomiarów wykonanych dokładniejszymi przymiarami b) i c)
można sądzić, że jest wręcz przeciwnie – długość zmierzona przez drugą osobę jest bliższa długo-
ściom otrzymanym przyrządami dokładniejszymi.
Oczywiście ocena szerokości przedziału granicznego nie musi być zawsze ułamkiem działki ele-
mentarnej. W niektórych przypadkach rozsądnym może być przyjęcie wartości nawet wielokrotnie
większej niż wartość działki elementarnej. Dużo będzie zależało od warunków wykonywania pomiaru
i samego obiektu badanego. Prześledźmy to na kilku prostych przykładach.
a)
Za pomocą przymiaru milimetrowego mierzymy długość
v karty kredytowej.
Ponieważ karta ma małe rozmiary i prosty kształt, możemy łatwo przyłożyć do niej przymiar
(lub kartę do przymiaru), a dzięki temu, że jest płaska i ma ostre, wyraźne krawędzie stosun-
kowo łatwo odczytamy położenie jej krawędzi na tle skali przymiaru. W takim przypadku, dla
większości osób nie będzie stanowiło problemu dokonanie odczytu z dokładnością do
1 5
⁄ (lub 1/4) działki, czyli Δ = 0,20 mm (lub Δ = 0,25 mm). Oznacza to niepewność
standardową
v ≈ 0,082 mm (lub v ≈ 0,10 mm).
b)
Za pomocą przymiaru milimetrowego mierzymy szerokość
v kostki mydła.
Odczyt nie jest teraz tak łatwy jak poprzedni. Mydło jest grubsze od karty kredytowej, ma za-
okrąglone krawędzie i odczyt położeń tych krawędzi jest bardziej subiektywny niż poprzedni.
Różne osoby mogą dostać wyniki różniące się nawet o wartość
2 ÷ 3 mm. Rozsądniejsze bę-

Obliczanie i wyrażanie niepewności pomiarowych
20
Jeśli wykonujemy pomiar prostym przyrządem mechanicznym, wkład do niepewności pomiaru
wynikający z niepewności odczytu z tego przyrządu oceniamy metodą B w następujący sposób:
1)
Dokonujemy odczytu z dokładnością do działki elementarnej lub, o ile to możliwe z do-
kładnością do ułamka (np. do
1 2
⁄ , 1 4
⁄ , 1 5
⁄ działki elementarnej.
2)
Szacujemy położenie końców przedziału granicznego (na ogół symetrycznie względem
odczytanej wartości) i określamy jego szerokość
Δ .
3)
Zakładając trójkątny rozkład prawdopodobieństwa liczymy niepewność standardową ze
wzoru:
=
Δ
√6
.
dzie teraz przyjęcie, że połowa szerokości granicznej jest rzędu np.
Δ ≈
O
W
∙ 3 mm = 1,5 mm,
co daje niepewność standardową pomiaru na poziomie
v = 1,5 mm √6
⁄
≈ 0,61 mm.
c)
Za pomocą taśmy mierniczej mierzymy długość
v pokoju. Podobnie jak w poprzednich przy-
padkach działka elementarna przyrządu ma wartość
1 mm, jednak teraz mamy do czynienia z
pomiarem długości stosunkowo dużego odcinka. Intuicyjnie wyczuwamy, że nie jesteśmy w
stanie dokonać tego pomiaru z dokładnością rzędu
1 mm, chociażby dlatego, że sam pokój
nie jest wykonany z taką dokładnością. Najlepiej byłoby w tym wypadku, gdybyśmy wykonali
serię pomiarów i opracowali ją metodą A. Jeśli jednak nie mamy takiej możliwości musimy
oszacować niepewność pomiaru zgodnie z naszą wiedzą i doświadczeniem zdobytym np. na
podstawie wcześniejszych pomiarów tego typu. Można też spróbować wykonać kilka
2 ÷ 4
pomiarów, które dałyby nam podstawę do określenia niepewności granicznej i na tej pod-
stawie oszacować niepewność standardową przyjmując
v = Δ √6
⁄ .
Podsumujmy nasze rozważania.
Uwaga
►
W przypadku niektórych mechanicznych przyrządów pomiarowych nie możemy zakładać
trójkątnego rozkładu prawdopodobieństwa, który stosowaliśmy w Przykładzie 1. Przykładem takiego
przyrządu jest stoper mechaniczny. Wskazówka takiego stopera nie porusza się płynnie, lecz przeska-
kuje każdorazowo o jedną działkę (np. o
0,2 s). Odczytując wskazanie stopera nie jesteśmy w stanie
określić w jakim momencie czasu odpowiadającym sąsiednim kreskom skali zatrzymaliśmy stoper. W
takim przypadku mamy do czynienia z prostokątnym rozkładem prawdopodobieństwa, czyli niepew-
ność standardową będziemy liczyć ze wzoru
=
w ł5 S S SIx I
√3
.
5.2.3
Analogowe mierniki elektryczne
W przypadku analogowych mierników elektrycznych spotykamy się z tym samym problemem
niepewności odczytu, co w przypadku mierników mechanicznych. Wiemy już jak oceniać ten wkład
do niepewności. Do tej niepewności musimy dodać niepewność związaną z procesem wzorcowania
przyrządu. W przypadku analogowych przyrządów elektrycznych jest to zwykle parametr nazywany
klasą przyrządu
. Klasa przyrządu jest liczbą umieszczaną zwykle przez producenta miernika pod skalą
przyrządu, obok innych oznaczeń charakteryzujących miernik. W przypadku mierników laboratoryj-

Wprowadzenie do metod opracowywania danych pomiarowych
21
Pamiętaj
Niepewność standardowa złożona z n niepewności standardowych jest równa pierwiastkowi z
sumy kwadratów tych niepewności (wariancji poszczególnych rozkładów)
0
= B
O
W
+
W
W
+ ⋯ +
M
W
= K
L
W
M
LNO
.
nych jest to liczba mniejsza od 1, np. 0,5 lub 0,2. Klasa przyrządu pozwala na oszacowanie maksymal-
nego błędu określonego przez producenta w procesie wzorcowania przyrządu, jaki możemy popełnić
podczas pomiaru tym przyrządem. Związana z tym błędem połowa niepewności granicznej
Δ
zC
wy-
nosi
Δ
zC
=
5 b w/ wą ∙ w 5 Sb
100
.
Zakres oznacza wartość danej wielkości fizycznej, np. natężenia prądu elektrycznego, przy której
wskazówka miernika znajduje się na końcu skali. Zwykle mierniki elektryczne mają możliwość usta-
wienia zakresu, na którym będziemy pracować. Ponieważ nie mamy żadnych informacji na temat
możliwego rozkładu prawdopodobieństwa musimy założyć prostokątny rozkład, w związku z czym
niepewność standardowa związana z tym wkładem do niepewności pomiaru wynosi
x =
Δ
zC
√3
=
5 b w/ wą ∙ w 5 Sb
100 ∙ √3
.
5.11
Obie niepewności, czyli niepewność związaną z trudnością odczytu ze skali analogowej oraz niepew-
ność wynikająca z klasy przyrządu są od siebie niezależne, więc wyznaczając niepewność pomiaru
musimy uwzględnić oba przyczynki. Ponieważ są to niepewności standardowe, to ich sumowanie
podlega prawu składania niepewności standardowych:
Stosując się do powyższej reguły sumowania niepewności standardowych możemy policzyć całkowitą
niepewność pomiaru analogowym miernikiem elektrycznym zgodnie ze wzorem
= B
|z}C}
W
+
zC}|}
W
,
5.12
gdzie
|z}C}
jest niepewnością związaną z trudnością odczytu wskazania, a
zC}|}
niepewno-
ścią związaną z klasą przyrządu.
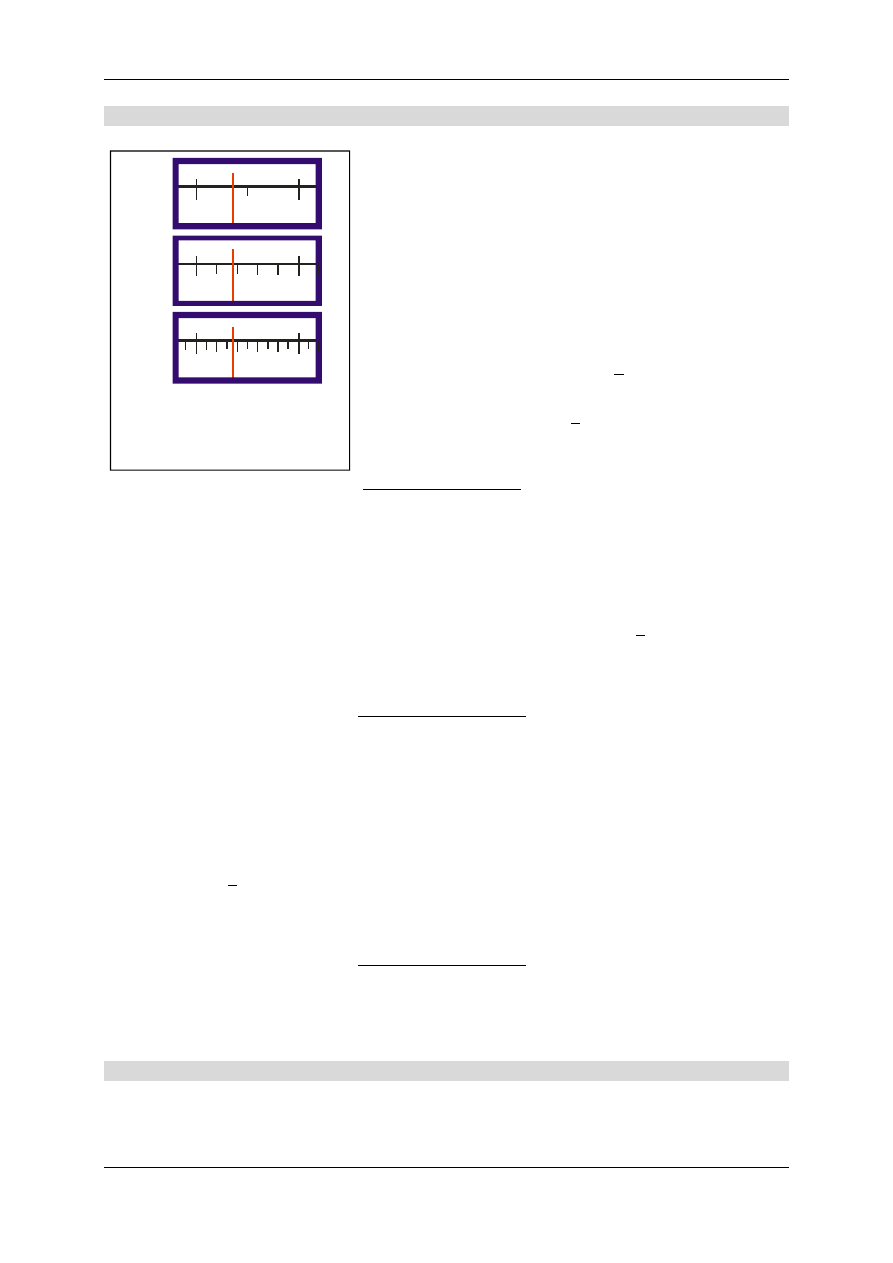
Obliczanie i wyrażanie niepewności pomiarowych
22
20
25
20
25
V
20
25
(a)
(b)
(c)
V
V
0,5
0,5
0,5
Rys. 4.6. Przykładowe wskazania
trzech woltomierzy analogowych
o klasie dokładności 0,5.
Przykład 2.
Wykonano pomiar napięcia elektrycznego trzema analogo-
wymi wolotomierzami. Wskazania tych woltomierzy poka-
zano na Rysunku 4.6. Liczba
0,5 widoczna na skalach przy-
rządów oznacza ich klasę. Podczas pomiaru każdy z wolto-
mierzy pracował na zakresie
50 V.
a)
Odczytano
4 = 20 V + 3 4
⁄ ∙ 2,5 V = 21,875 V.
Przyjęto wartość połowy szerokości przedziału granicznego
Δ4 = 1 4
⁄ ∙ 2,5 V = 0,625 V i trójkątny rozkład prawdopo-
dobieństwa. Niepewność standardowa związana z odczy-
tem wynosi
|z}C}
4 = 0,625 V √6
⁄
≈ 0,399 V. Niepew-
ność pomiaru związana z klasą przyrządu wynosi
zC}|}
4 = 0,5 ∙ 50 100 ∙ √3
⁄
≈ 0,144 V. Ostatecznie
niepewność pomiaru oszacowana metodą B jest równa
4 = k0,399
W
V
W
+ 0,144
W
V
W
≈ 0,424 V.
A zatem
4 = 21,88 42 V.
b)
Odczytano
4 = 21 V + 4 5
⁄ ∙ 1 V = 21,8 V. Przyjęto wartość połowy szerokości przedziału
granicznego
Δ4 = 1 5
⁄ ∙ 1 V = 0,20 V i trójkątny rozkład prawdopodobieństwa. Niepew-
ność standardowa związana z odczytem wynosi
|z}C}
4 = 0,20 V √6
⁄
≈ 0,0817 V. Nie-
pewność pomiaru związana z klasą przyrządu jest taka sama jak w przykładzie a) i wynosi
zC}|}
4 ≈ 0,144 V. Ostatecznie niepewność pomiaru jest równa
4 = k0,0817
W
V
W
+ 0,144
W
V
W
≈ 0,166 V.
A zatem
4 = 21,80 17 V.
c)
Odczyt oszacowano na
4 = 21,5 V + 2 4
⁄ ∙ 0,5 V = 21,75 V. Przyjęto wartość połowy sze-
rokości przedziału granicznego
Δ4 = 1 4
⁄ ∙ 0,5 V = 0,125 V i trójkątny rozkład prawdopo-
dobieństwa. Niepewność standardowa związana z odczytem wynosi
|z}C}
4 =
0,125 V √6
⁄
≈ 0,0510 V. Niepewność pomiaru związana z klasą przyrządu jest taka sama
jak w przykładzie a) i wynosi
zC}|}
4 ≈ 0,144 V. Ostatecznie niepewność pomiaru jest
równa
4 = k0,0510
W
V
W
+ 0,144
W
V
W
≈ 0,153 V.
A zatem
4 = 21,75 15 V.
Wprowadzenie do metod opracowywania danych pomiarowych
23
5.2.4
Elektroniczne mierniki cyfrowe
W przeciwieństwie do odczytu wskazań miernika analogowego, odczyt z miernika cyfrowego jest
jednoznaczny
15
. Nie oznacza to jednak, że nie ma niepewności związanej z odczytem. Przyrządy cy-
frowe muszą zamieniać sygnały ciągłe na dyskretne. Jest to nazywane dyskretyzacją. Istnieje pewien
określony zakres sygnałów wejściowych, dla których wskazanie przyrządu będzie takie same. Szero-
kość tego przedziału może być nawet większa niż tzw.
rozdzielczość miernika
(patrz niżej). Ta ostatnia
sytuacja dotyczy zwłaszcza pomiarów sygnałów zmiennych (np. napięć zmiennych), które trudniej się
dyskretyzuje. Maksymalna niepewność pomiaru związana z dyskretyzacją jest podawana przez pro-
ducenta najczęściej w postaci symbolu
dgt
(ang. digit, cyfra) poprzedzonego odpowiednią cyfrą, np.
1dgt, 3dgt itp. Odpowiadającą temu niepewność liczymy mnożąc cyfrę znajdującą się przed symbo-
lem dgt przez
rozdzielczość przyrządu
. Rozdzielczość przyrządu odpowiada wartości związanej z
ostatnią cyfrą znaczącą na wyświetlaczu, np. jeśli woltomierz pracuje na zakresie 2000 mV i wyświetla
4 cyfry, to jego rozdzielczość wynosi 1 mV. Drugą informacją podawaną przez producentów mierni-
ków cyfrowych, którą musimy wykorzystać licząc niepewność pomiaru jest maksymalna niepewność
względna (procentowa) wartości mierzonej. Jest to podawane zwykle w postaci symbolu
rdg
(ang.
read digits, odczytane cyfry) poprzedzonego liczbą podawaną w procentach np. 1,2% rdg. Fragment
przykładowej tabeli z podaną przez producenta dokładnością dla różnych typów pomiarów i różnych
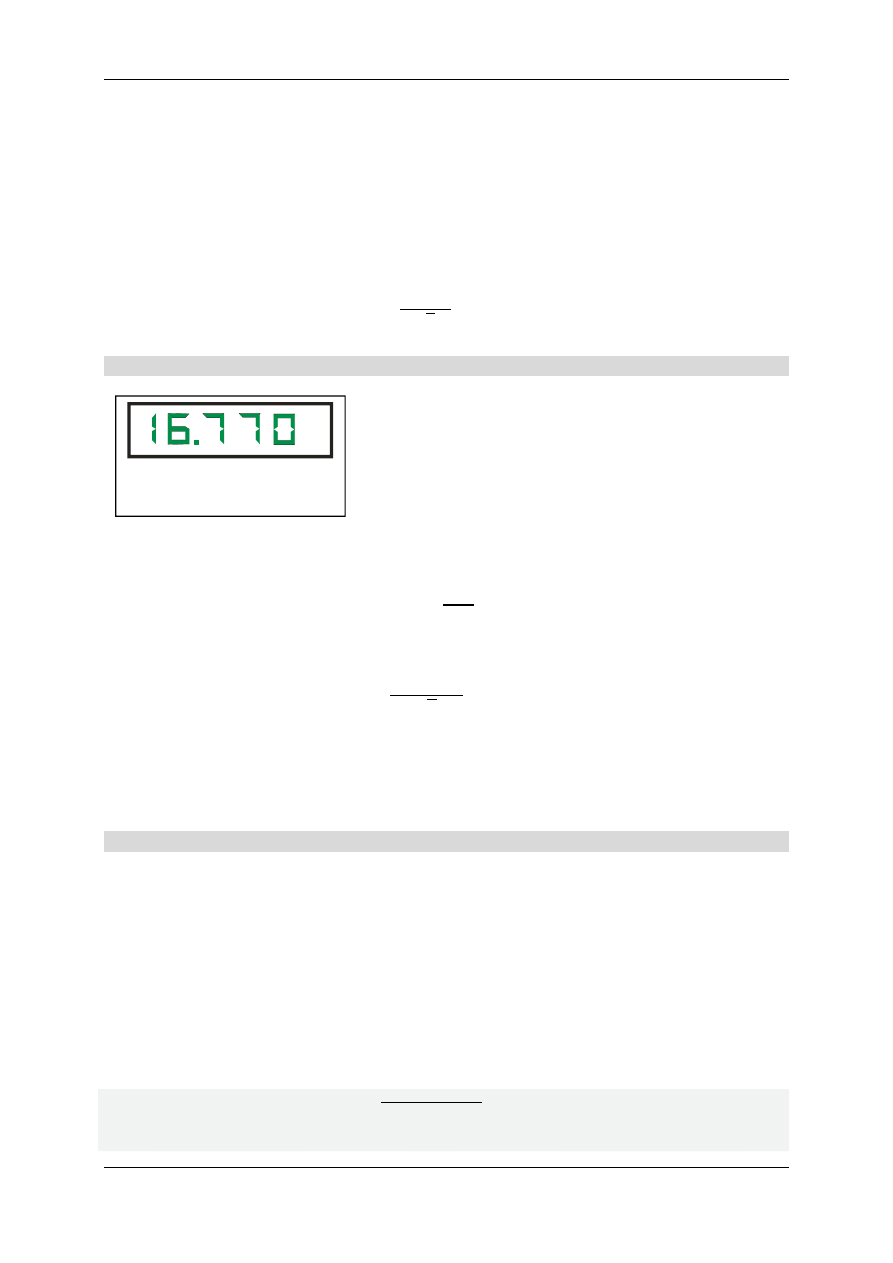
zakresów pracy laboratoryjnego multimetru cyfrowego MXD-4660A przedstawia Rysunek 4.7.
Rys. 4.7. Fragment tabeli dokładności laboratoryjnego multimetru cyfrowego MXD-4660A.
Producent tego miernika podaje dokładność miernika w zakresie temperatur
+23 ± 5℃. W przypad-
ku niektórych mierników cyfrowych producenci podają dodatkowo informację o niepewności wynika-
jącej z używania miernika w temperaturze innej niż temperatura cechowania. Informacja taka ma
najczęściej postać wzoru np.
0,01% ∙
− 23°C ∙ w 5 Sb.
15
Zdarza się, że warunki pomiaru albo niestabilność samej wielkości mierzonej sprawiają, że ostatnia lub kilka
ostatnich cyfr wyświetlacza przyrządu cyfrowego ciągle zmienia się podczas odczytu. W takim wypadku, o ile to
możliwe, powinniśmy ustalić granice tych zmian i na ich podstawie oszacować wartość zmierzoną oraz
uwzględnić te zmiany przy szacowaniu szerokości przedziału granicznego lub dokonać odczytu tylko stabilnej
części wyświetlanej wartości.
Obliczanie i wyrażanie niepewności pomiarowych
24
V
Rys. 4.8. Wskazanie miernika
cyfrowego.
W przypadku starszych typów mierników cyfrowych możemy się spotkać z innym sposobem po-
dawania dokładności miernika. Mogą to być dwie liczby
ƒ
O
i
ƒ
W
podawane w procentach oraz wzór
ƒ
O
∙ + ƒ
W
∙ w 5 Sb, np. dla omomierza cyfrowego typ 1321 mamy ± 0,2% ∙ + 0,1% ∙ zakres).
Niezależnie od tego, z którą z powyższych sytuacji się spotkamy, uważamy, że wyliczona na pod-
stawie podanych przez producenta informacji niepewność jest połową niepewności granicznej
Δ
D…}M.
. Wobec tego, przy założeniu rozkładu prostokątnego, niepewność standardową liczymy ze
wzoru
=
†
D…}M.
√3
.
5.13
Przykład 3.
Za pomocą laboratoryjnego multimetru cyfrowego MXD-
4660A wykonano pomiar napięcia stałego. Podczas pomia-
ru, miernik ustawiony był na zakresie 20 V i pracował w
temperaturze
21℃ (czyli w temperaturze mieszczącej się w
przedziale podanym przez producenta). Stan wyświetlacza
miernika pokazano na Rysunku 4.8.
Korzystając z tabeli pokazanej na Rysunku 4.7 znajdujemy połowę niepewności granicznej
Δ4
D…}M
= 0,05% ∙ 16,770 V + 3 ∙ 1 mV =
0,05
100 ∙ 16,770 V + 3 ∙ 0,001 V ≈ 0,01139 V.
Niepewność standardowa tego pomiaru wynosi
4 =
0,01139 <
√3
≈ 0,00657 V.
Ostatecznie mamy
4 = 16,7700 66 V.
Zwróćmy uwagę, że w powyższych wzorach
4 oznacza napięcie, a nie niepewność rozszerzoną.
5.3
Sumowanie składników niepewności
Niepewność wyniku pomiaru na ogół składa się z szeregu składników. Każdy z nich przedsta-
wiamy w postaci niepewności standardowej. Niektóre z nich mogą być wyznaczone metodą A, a inne
metodą B. Po ich wyliczeniu musimy je zsumować. Sumowanie niepewności standardowych wykonu-
jemy sumując kwadraty tych niepewności, a następnie pierwiastkując otrzymaną sumę. Jeśli np. obli-
czyliśmy metodą A niepewność
‡
uwzględniającą rozrzut statystyczny wartości mierzonych
oraz metodą B, niepewność
ˆ
wynikającą z dokładności użytego przyrządu i są to jedyne składni-
ki niepewności, to ostatecznie niepewność standardowa pomiaru wyniesie
= B
‡
W
+
ˆ
W
.
5.14

Wprowadzenie do metod opracowywania danych pomiarowych
25
6.
Ocena niepewności standardowej pomiaru pośredniego
Najczęściej wykonywanymi pomiarami są pomiary pośrednie. Pomiar taki polega na wykona-
niu pomiarów bezpośrednich innych wielkości fizycznych, a następnie wyliczeniu wartości wielkości
mierzonej (pośrednio) z wzoru, który łączy tę wielkość z pozostałymi wielkościami zmierzonymi bez-
pośrednio. Przypomnijmy przykłady pomiarów pośrednich, które podaliśmy w podrozdziale 1.4.
•
Aby wyznaczyć objętości V kuli możemy zmierzyć (bezpośrednio) jej średnicę D i skorzystać ze
wzoru na objętość kuli:
< =
=‰
?
@
.
•
Aby wyznaczyć wartość przyśpieszenia ziemskiego g możemy zmierzyć okres tzw. małych
drgań wahadła prostego oraz jego długość l. Jeśli średnica kulki wahadła prostego będzie
odpowiednio mała w porównaniu z długością nitki, a wychylenia będą odpowiednio małe, to
okres drgań tego wahadła będzie z dobrym przybliżeniem równy okresowi drgań harmonicz-
nych wahadła matematycznego
= 2AB
C
D
. Przekształcając ten wzór dostajemy:
E =
F=
G
C
G
.
Otrzymany związek pozwala nam wyznaczyć metodą pośrednią wartość przyśpieszenia ziem-
skiego.
Załóżmy, że wielkość
/, której wartość chcemy wyznaczyć za pomocą pomiaru pośredniego jest po-
wiązana z
Š wielkościami fizycznymi
O
,
W
, … ,
Œ
, które możemy zmierzyć bezpośrednio, zależnością
funkcyjną
/ = P
O
,
W
, … ,
Œ
6.1
W podanych powyżej przykładach byłyby to zależności
<(•) =
=‰
?
@
i
E( , ) =
F=
G
C
G
. W celu wyzna-
czenia wartość wielkości
/ wykonujemy pomiary bezpośrednie wielkości
O
,
W
, … ,
Œ
. Niech wyniki
pomiarów tych wielkości wynoszą:
̅
O
, ̅
W
, … , ̅
Œ
, a niepewności standardowe tych pomiarów wyno-
szą
(
O
), (
W
), … , (
Œ
). Dobrą estymatą wartości wielkości / będzie wartość funkcji
P(
O
,
W
, … ,
Œ
) wyliczonej w punkcie ( ̅
O
, ̅
W
, … , ̅
Œ
)
/2 = P( ̅
O
, ̅
W
, … , ̅
Œ
).
(6.2)
W naszych przykładach będą to wartości wyliczone następująco:
<2 =
=‰Ž
?
@
i
E̅ =
F=
G
C̅
2
G
.
Nieco trudniej będzie oszacować niepewność standardową pomiaru pośredniego wielkości
/. Nie-
pewności standardowe
(
O
), (
W
), … , (
Œ
) wielkości mierzonych bezpośrednio, przenoszą się na
wielkość
/, przez co wartość /2 będzie również obarczona niepewnością. Przenoszenie się niepewno-
ści standardowych wielkości mierzonych bezpośrednio na niepewność standardową wielkości mie-
rzonej pośrednio opisuje tzw.
prawo propagacji niepewności
. W sytuacji, gdy wielkości
O
,
W
, … ,
Œ
,
są niezależne (nieskorelowane), tzn. wtedy, gdy np. pomiar żadnej z nich nie wpływa na pomiary po-
zostałych
16
, prawo propagacji niepewności standardowych opisane jest poniższym wzorem
0
(/) = dK[•
L
(
L
)\
W
Œ
LNO
,
(6.3)
16
W większości ćwiczeń laboratoryjnych wykonywanych w naszym laboratorium założenie to jest słuszne.

Obliczanie i wyrażanie niepewności pomiarowych
26
gdzie
•
L
są tzw.
współczynnikami wrażliwości
. Współczynnik wrażliwości
•
L
jest równy pochodnej
cząstkowej funkcji
P
O
,
W
, … ,
Œ
po zmiennej
L
wyliczonej w punkcie
̅
O
, ̅
W
, … , ̅
Œ
•
L
≡
•P
•
L
‘
U̅
’
,U̅
G
,…,U̅
“
.
6.4
Niepewność wyliczoną wzorem (5.3) nazywamy
złożoną niepewnością standardową
i oznaczamy
symbolem
0
(/), gdzie / jest symbolem lub nazwą zmiennej mierzonej pośrednio.
Znajdźmy wzory na złożoną niepewność standardową dla obu, podanych na wstępie tego podrozdzia-
łu przykładów.
Uwaga: W większości ćwiczeń wyprowadzenie wzorów na niepewność złożoną nie będzie wymagało
liczenia pochodnych cząstkowych. Wystarczy opanować wzory podane w podrozdziałach 5.1 i 5.2
oraz wiedzieć, w jakich przypadkach można je stosować. Tam gdzie liczenie pochodnych cząstkowych
byłoby konieczne, gotowe wyrażenia na niepewność złożoną będą podane w instrukcji do ćwiczenia.
Przykład 1
Funkcja
<(•) = A•
t
/6 jest funkcją jednej zmiennej, więc zamiast pochodnej cząstkowej li-
czymy zwykłą pochodną
<
• =
A
2 •
W
.
A zatem
0
(<) = r”
A
2 •
Ž
W
•
W
∙
W
(•) =
A
2 •
Ž
W
(•).
Przykład 2
Pochodna cząstkowa funkcji
E( , ) = 4A
W
/
W
po zmiennej wynosi
•E
• =
4A
W
W
,
a pochodna cząstkowa tej funkcji po zmiennej wynosi
•E
• = −
8A
W
t
.
A zatem
0
(E) = r–
4A
W
2
W
—
W
W
( ) + –−
8A
W
̅
2
t
—
W
W
( ) ,
lub po przekształceniu
0
(E) =
4A
W
̅
2
W
r–
( )
̅ —
W
+ –
2 ( )
2
W
—
W
= E̅ ∙ r–
( )
̅ —
W
+ –
2 ( )
2
W
—
W
.

Wprowadzenie do metod opracowywania danych pomiarowych
27
6.1
Funkcja będąca sumą zmiennych niezależnych
W najprostszej sytuacji funkcja wyrażająca związek pomiędzy wielkością
/ mierzoną pośrednio, a
wielkościami
O
,
W
, … ,
Œ
jest liniową funkcją tych ostatnich
/ = P
O
,
W
, … ,
Œ
=
O O
+
W W
+
t t
+ ⋯ = K
L L
M
LNO
.
6.5
W takim przypadku mamy
•P
•
L
=
L
.
6.6
A zatem
0
/ = B
O
W W
O
+
W
W W
W
+
t
W W
t
+ ⋯ = dK
L
W W
L
Œ
LNO
.
6.7
Przykład 3
Zmierzono długość wahadła prostego mierząc długość nitki
b oraz średnicę kulki, zawieszo-
nej na tej nitce. Długość wahadła znajdujemy ze wzoru
= b + /2.
Jak widzimy jest to sytuacja opisana w równaniu (5.5), a zatem niepewność standardową po-
miaru pośredniego długości wahadła możemy wyliczyć korzystając z wzoru (6.7).
= r
W
b +
1
4
W
.
6.2
Funkcja będąca iloczynem potęg zmiennych niezależnych
Bardzo często spotykanym przypadkiem, jest funkcja będąca iloczynem potęg zmiennych niezależ-
nych
/ = P
O
,
W
, … ,
Œ
= ˜ ∙
O
’
∙
W
G
∙ … ∙
Œ
“
= ˜ ™
L
š
Œ
LNO
.
6.8
W takim przypadku
•P
•
L
= ˜ ∙
O
’
∙
W
G
∙ … j
L L
š
TO
… ∙
Œ
“
=
j
L
L
∙ ˜ ∙
O
’
∙
W
G
∙ … ∙
Œ
“
=
j
L
L
∙ /.
6.9
A zatem

Obliczanie i wyrażanie niepewności pomiarowych
28
/ = r–
j
O
O
∙ / ∙
O
—
W
+ –
j
W
W
∙ / ∙
W
—
W
+ ⋯ + –
j
Œ
Œ
∙ / ∙
Œ
—
W
.
6.10
Czyli po przekształceniu
/ = |/| ∙ r–j
O
(
O
)
O
—
W
+ –j
W
(
W
)
W
—
W
+ ⋯ + –j
Œ
(
Œ
)
Œ
—
W
.
6.11
Powyższy przepis liczenia niepewności podaje się często w postaci wzoru na standardową niepew-
ność względną
/
|/| =
r–j
O
(
O
)
O
—
W
+ –j
W
(
W
)
W
—
W
+ ⋯ + –j
Œ
(
Œ
)
Œ
—
W
.
6.12
Zauważmy, że funkcje w Przykładach 1 i 2 mają omawianą powyżej postać i można dla nich zastoso-
wać wyrażenie (6.11), zaś zastosowanie tego wyrażenia do funkcji z Przykładu 3 byłoby błędem.
UWAGA
►
Wzory (6.11) i (6.12) można stosować jedynie w przypadku funkcji o postaci określonej
wzorem (6.8)
Przykład 4
Funkcja
< • = A•
t
/6 z Przykładu 1 ma postać typu (6.8), więc zgodnie z wyrażeniem (6.10)
< = < ∙ r–3 ∙
•
• —
W
= 3 ∙ < ∙
•
• = 3 ∙
A•
t
6 ∙ • =
A•
W
2
• .
Jak widać otrzymaliśmy wyrażenie takie samo jak w Przykładzie 1.
Przykład 5.
Również funkcja
E ,
=
F=C
G
= 4A
W O TW
z Przykładu 2 ma postać (6.8) .A zatem
E = E ∙ r–
—
W
+ –−
2
—
W
co jest zgodne z wynikiem otrzymanym w Przykładzie 2.
Przykład 6.
Funkcja
b,
= b + /2 z Przykładu 3 nie ma postaci (6.8). Gdybyśmy do tej funkcji zastoso-
wali wyrażenie (6.10), to dostalibyśmy
= ∙ r–
b
b —
W
+ –
—
W
= ›b + 2œ ∙ r–
b
b —
W
+ –
—
W
.
Jak widzimy, otrzymane wyrażenie różni się od poprawnego wyrażenia, które otrzymaliśmy w
Przykładzie 3

Wprowadzenie do metod opracowywania danych pomiarowych
29
mg
(a)
(b)
mg
Rys. 7.1. Dwa wskazania wagi cyfrowej.
›b + 2œ ∙ r–
b
b —
W
+ –
—
W
≠ r
W
b +
1
4
W
.
7.
Podawanie wyniku pomiaru
7.1
Cyfry znaczące
Rozważmy wskazania wagi cyfrowej o rozdzielczości wskazań
1 mg przedstawione na Rys. 7.1. W
pierwszym przypadku, z wyświetlacza wagi odczytaliśmy masę ważonego obiektu –
482 mg. Ważąc
inny podobny obiekt odczytaliśmy masę
480 mg (patrz Rysunek 6.1 (b)). O cyfrach 4, 8, 2, w pierw-
szym przypadku i cyfrach
4, 8, 0, w drugim przypadku mówimy, że są
cyframi znaczącymi
naszych
wartości zmierzonych. Jest oczywiste, że pomięcie, którejś z nich byłoby błędem.
Zapiszmy teraz oba odczyty w różnych jednostkach wtór-
nych masy w układzie SI (patrz punkt 3). Np. w miligramach
(mg), gramach (g), dekagramach (dag) i kilogramach (kg). W
pierwszym przypadku nasz odczyt zapiszemy następująco:
a)
482 mg, 0,482 g, 0,0482 dag, 0,000482 kg,
Zauważmy, że każdej z tych liczb występują cyfry
4, 8, 2,
które nazwaliśmy cyframi znaczącymi naszego wyniku.
Zmienia się jedynie położenie przecinka. W każdej z poda-
nych liczb jedynie cyfry
4, 8, 2, są cyframi znaczącymi. Dodatkowe zera, jakie pojawiają się przed na-
szymi cyframi (przy zapisie w dag i kg) nie są cyframi znaczącymi. Nie wnoszą one niczego nowego do
wyniku pomiaru, ich pojawienie się wynika tylko z mnożników dziesiętnych poszczególnych jednostek
masy, a nie z samego pomiaru.
Jeśli teraz w podobny sposób zapiszemy odczyt b), to musimy konsekwentnie w każdym z tych zapi-
sów podać wszystkie cyfry znaczące, czyli w tym wypadku
4, 8, 0
b)
480 mg, 0,480 g, 0,0480 dag, 0,000480 kg,
Zapis wyników w postaci
0,480 g, 0,0480 dag, 0,000480 kg, z podaniem zera na ostatniej pozycji
podkreśla fakt, że to zero jest cyfrą znaczącą, gdyż odczyt wykonany był z dokładnością do
1 mg, czyli
0,001 g, 0,0001 dag, 0,000001 kg. To ostatnie zero (lub ostatnie zera) musimy koniecznie zapisać.
Aby zapamiętać tę regułę rozważmy jeszcze inny przykład: wyświetlacz wagi pokazał masę 8000 g.
Jeśli zapisalibyśmy tę masę jako
8 kg, to zgubilibyśmy informację o dokładności tego pomiaru. Aby
poprawnie podać tę masę w kilogramach musimy ją zapisać w postaci
8,000 kg. Dopiero taki zapis
będzie odpowiadał naszemu odczytowi masy w gramach, gdyż obie liczby:
8000 g i 8,000 kg mają
tyle samo (cztery) cyfr znaczących. Liczba
8 kg ma tylko jedną cyfrę znaczącą, co sugeruje, że nie-
pewność pomiaru jest rzędu
1 kg.
Opisane tu reguły dotyczą nie tylko zapisu odczytu wskazań miernika podczas pomiarów bezpo-
średnich. W taki sam sposób musimy postępować, gdy zapisujemy wynik pomiaru pośredniego, któ-
rego wartość otrzymujemy na drodze obliczeń. Ale w takim przypadku nie wiemy z góry ile cyfr zna-
czących ma wynik, dowiemy się tego dopiero wówczas, gdy policzymy niepewność tego pomiaru.

Obliczanie i wyrażanie niepewności pomiarowych
30
Pamiętaj
Cyframi znaczącymi
liczby odnoszącej się do wartości mierzonej wielkości są wszystkie cy-
fry począwszy od pierwszej cyfry niezerowej.
Końcowe zera liczby są też cyframi znaczącymi i zawsze należy je podawać.
Niepewność pomiaru zaokrąglamy zawsze do dwóch cyfr znaczących
Po zaokrągleniu niepewności zaokrąglamy wartość mierzoną. Robimy to z dokładnością
do tego samego miejsca rozwinięcia dziesiętnego, do którego zaokrągliliśmy niepewność.
Wartość niepewności będzie decydować o tym, do której cyfry musimy zaokrąglić wartość zmierzoną
(patrz punkt 7.2).
UWAGA
►
Nie należy utożsamiać cyfr znaczących z cyframi po przecinku! Ten często popełniany błąd
wynika z niezrozumienia pojęcia cyfr znaczących.
Na zakończenie wróćmy do przykładów obu odczytów
482 mg i 480 mg. Każda z tych liczb ma
trzy cyfry znaczące. Zapisanie tych liczb w jednostkach większych niż
mg nie stanowiło problemu,
gdyż sprowadzało się jedynie do odpowiedniego przesunięcia przecinka w lewo i ewentualnego dopi-
sania zer poprzedzających nasze cyfry znaczące. Załóżmy teraz, że chcemy podać nasze wyniki w
μg.
Zapisy naszych odczytów w postaci liczb
482000 μg i 480000 μg są niepoprawne gdyż tak podane
liczby mają 6 cyfr znaczących i sugerują dokładność pomiaru rzędu
1 μg. Nasze liczby powinny mieć 3
cyfry znaczące niezależnie od jednostki w jakiej podamy wynik. W sytuacji, gdy ten wynik chcemy
podać w
μg, to powinniśmy zastosować zapis typu
a)
0,482 ∙ 10
@
μg lub 482 ∙ 10
t
μg
b)
0,480 ∙ 10
@
μg lub 480 ∙ 10
t
μg,
dzięki czemu liczba cyfr znaczących (w tym przypadku 3) będzie właściwa.
7.2
Zaokrąglenia wyników pomiaru
Po wykonaniu wszystkich obliczeń należy zaokrąglić wartość niepewności pomiaru oraz mierzonej
wielkości i zapisać wynik zgodnie z przyjętymi zasadami, a także podać dodatkowe informacje nie-
zbędne do pełnej interpretacji wyniku i jego wykorzystania przez przewidywanych użytkowników
tego wyniku. Zarówno estymata wartości wielkości mierzonej jak i niepewność jej pomiaru nie po-
winny być podawane z nadmierną liczbą cyfr. Zgodnie z przyjętą w Przewodniku zasadą niepewność
zaokrąglamy zawsze do dwóch cyfr znaczących. Wartość zmierzoną zaokrąglamy do tego samego
miejsca rozwinięcia dziesiętnego, do którego zaokrągliliśmy niepewność pomiaru.
UWAGA
►
Jeżeli po zaokrągleniu niepewności jej drugą cyfrą znaczącą jest zero, to należy ją zapisać.
Podobnie jest z zaokrągleniem wartości mierzonej. Jeśli jej ostatnią cyfrą (lub ostatnimi cyframi) jest
zero, to należy ją (należy je) zapisać.
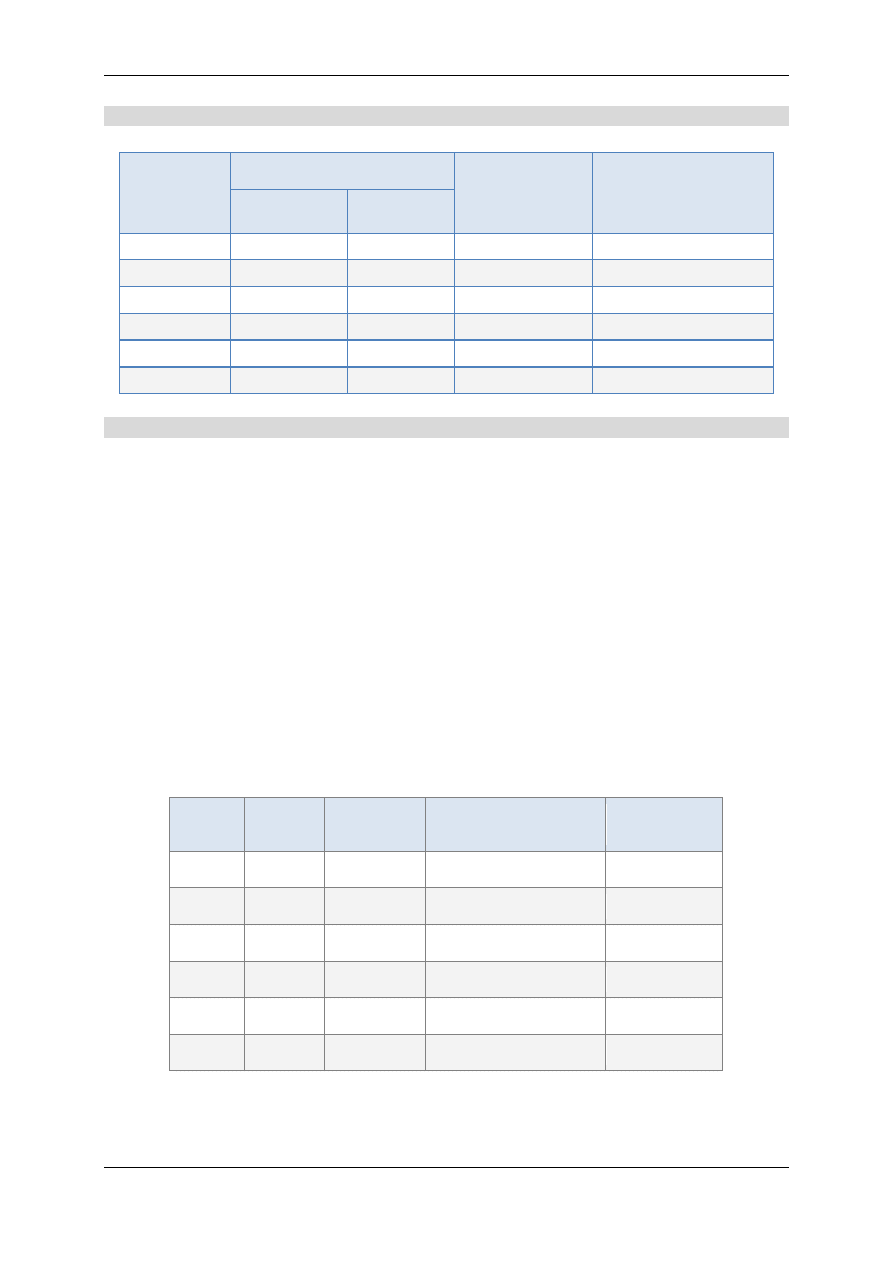
Wprowadzenie do metod opracowywania danych pomiarowych
31
Przykład 1.
Wartość zmie-
rzona przed
zaokrągleniem
Niepewność pomiaru
Wartość zmierzona
po zaokrągleniu
Zapis wyniku
przed zaokrągle-
niem
po zaokrągleniu
7,34553 V
0,02876 V
0,029 V
7,346 V
4 = 7,346 29 V
1356,033 mT
18,761 mT
19 mT
1356 mT
= 1356 19 T
1000,023 kg/m
3
0,9952 kg/m
3
1,0 kg/m
3
1000,0 kg/m
3
¢ = 1000,0 10 kg/m
t
0,0880134 mm
0,0035872 mm
0,0036 mm
0,0880 mm
= 0,0880 36 mm
342753,22 Pa
1388,201 Pa
14 hPa
3428 hPa
= 3428 14 hPa
34,999 Hz
0,22345 Hz
0,22 Hz
35,00 Hz
P = 35,00 22 Hz
7.3
Stosowanie jednostek wtórnych
Każdy wynik pomiaru, obowiązkowo musi zawierać jednostkę miary, w jakiej podajemy wartość
zmierzoną i niepewność pomiaru. Powinniśmy używać jednostek miar układu SI. Nie musimy stoso-
wać wyłącznie jednostek podstawowych (np. m), możemy stosować
jednostki wtórne
(np. mm za-
miast m). To samo dotyczy
jednostek pochodnych
np. zamiast jednostki np.
kg/m
t
możemy użyć
jednostki
g/cm
t
jeśli zapis wyniku pomiaru w takiej jednostce będzie bardziej czytelny. Wyniki po-
miarów najlepiej podawać w takich jednostkach, żeby wartość liczbowa wartości mierzonej mieściła
się w przedziale od 0,1 do 1000. Dla przykładu lepiej napisać
ƒ = 456 pF zamiast
ƒ = 0,000 000 000 456 F, czy ¢ = 19,3 ∙ g/cm
t
zamiast
¢ = 19,3 ∙ 10
t
kg/m
t
. Najczęściej używa-
ne przedrostki jednostek wtórnych przedstawia tabela 3.1.
Tabela 3.1. Najczęściej używane przedrostki jednostek wtórnych.
a)
Mnożniki zwiększające
Nazwa
Symbol
Mnożnik
Przykład
Stosowane
od roku
tera
T
10
12
TB – terabajt
1975
giga
G
10
9
GHz – gigaherc
1960
mega
M
10
6
MW – megawat
1960
kilo
k
10
3
kV – kilowolt
1795
hekto
h
10
2
hPa – hektopaskal
1795
deka
da
10
1
dag – dekagram
1795

Obliczanie i wyrażanie niepewności pomiarowych
32
Przyśpieszenie ziemskie jest równe
E = 9,88 m/s
W
z niepewnością
0,35 m/s
W
.
E = 9,88 m/s
W
;
E = 0,35 m/s
W
.
E = 9,88 35 m/s
W
.
Przyśpieszenie ziemskie jest równe
E = 9,88 m/s
W
z niepewnością rozszerzoną
0,70 m/s
W
.
E = 9,88 m/s
W
;
4 E = 0,70 m/s
W
.
E = 9,88 ± 0,70 m/s
W
.
E = 9,88 m/s
W
;
4 E = 0,79 m/s
W
. Współczynnik rozszerzenia
5 = 2,26.
Zapis z użyciem symbolu
± zaleca się stosować jedynie w przypadku niepewności rozszerzo-
nej. Jeśli współczynnikiem rozszerzenia była liczba inna niż
2, to zaleca się podawanie tej licz-
by.
b)
Mnożniki zmniejszające
Nazwa
Symbol
Mnożnik
Przykład
Stosowane
od roku
decy
d
10
-1
dB – decybel
1795
centy
c
10
-2
cm – centymetr
1795
mili
m
10
-3
mm – milimetr
1795
mikro
µ
10
-6
µm – mikrometr
1960
nano
n
10
-9
nF – nanofarad
1960
piko
p
10
-12
pF – pikofarad
1960
7.4
Podawanie wyniku pomiaru, gdy miarą niepewności jest niepew-
ność standardowa
Zalecane sposoby zapisu wyniku pomiaru, gdy miarą niepewności pomiaru jest niepewność stan-
dardowa podajemy na poniższym przykładzie:
W trzecim, tzw. skróconym zapisie wyniku pomiaru, liczba w nawiasie jest wartością niepewności
standardowej odnoszącą się do ostatnich cyfr podawanego wyniku.
7.5
Podawanie wyniku pomiaru, gdy miarą niepewności jest niepew-
ność rozszerzona
Podobnie jak zrobiliśmy to w przypadku zapisu wyniku pomiaru z niepewnością standardową te-
raz podamy przykłady zapisu wyniku pomiaru, gdy podajemy niepewność rozszerzoną

Wprowadzenie do metod opracowywania danych pomiarowych
33
UWAGI:
1)
Zapis skrócony z zapisem dwóch cyfr niepewności w nawiasach stosujemy tylko dla nie-
pewności standardowej.
2)
Zapis z użyciem symbolu
± stosujemy tylko dla niepewności rozszerzonej.
3)
Zgodnie z Rozporządzeniem Rady Ministrów z dnia 30 listopada 2006 r. w sprawie legal-
nych jednostek miar:
a.
przy zapisywaniu wartości wielkości należy zostawić odstęp między wartością liczbową
a oznaczeniem jednostki miary. Wyjątkiem są oznaczenia jednostki miary kąta: stopnia,
minuty i sekundy.
b.
nazwę jednostki miary pisze się małą literą
17
, jeżeli ogólne reguły pisowni polskiej nie
stanowią inaczej
18
.
c.
w druku jednostki piszemy czcionką prostą.
d.
nazwy jednostek miar odmienia się zgodnie z zasadami deklinacji polskiej, np. 100 gra-
mów, a nie 100 gram.
8.
Uśrednianie wyników
Czasami zdarza się, że dysponujemy kilkoma wynikami pomiaru, tzn. mamy kilka estymat
wartości wielkości mierzonej oraz ich niepewności, np.
O
,
O
,
W
,
W
… ,
M
,
M
i chcemy
uśrednić te wyniki, tzn. znaleźć jedną, uśrednioną estymatę wartości wielkości mierzonej i jej nie-
pewność
,
. Aby uśrednić estymaty wartości wielkości mierzonej, musimy uwzględnić fakt, że
estymaty o niższej niepewności są ważniejsze od tych z większymi niepewnościami. Dlatego zamiast
średniej arytmetycznej powinniśmy policzyć tzw. średnią ważoną z wagami faworyzującymi wyniki
pomiarów o niższej niepewności. W tym przypadku najodpowiedniejszą będzie średnia ważona liczo-
na według wzoru
=
∑
L L
TW
M
LNO
∑
L
TW
M
LNO
.
Niepewność standardowa takiej średniej ważonej wyraża się wzorem
=
1
B∑
L
TW
M
LNO
.
9.
Porównywanie wyników
Błędy pomiarowe sprawiają, że wartości mierzonej wielkości uzyskane w wyniku różnych pomia-
rów nie są najczęściej identyczne. Jest tak nawet wówczas, gdy pomiary przeprowadzono taką samą
metodą pomiarową i w identycznych warunkach. Nie możemy zatem porównywać wyników pomia-
rów danej wielkości fizycznej w sensie równości matematycznej. W szczególności porównując nasz
wynik pomiaru z wartością tablicową mierzonej przez nas wielkości nie możemy się spodziewać, że
nasz wynik będzie identyczny z wynikiem tablicowym. Wynika, to chociażby z tego, że nasz pomiar
ma większą niepewność niż pomiary, których wyniki zamieszczone są w tablicach, a co za tym idzie
17
np. gram, metr, sekunda, niuton, tesla, amper, ale w skrótach g, m, s, N, T, A.
18
np. w zdaniu „Metr jest jednostką długości w układzie SI” – metr jest napisany z dużej litery, gdyż słowo to
rozpoczyna zdanie.

Obliczanie i wyrażanie niepewności pomiarowych
34
ma mniejszą liczbę cyfr znaczących. Dwa wyniki możemy porównywać tylko w sensie statystycznym.
Nie wnikając w szczegóły, możemy powiedzieć, że dwa wyniki pomiaru wielkości : pierwszy
O
z
niepewnością standardową
O
i drugi
W
z niepewnością standardową
W
są z dużym prawdo-
podobieństwem ze sobą zgodne, jeśli przedziały
1
O
−
O
,
O
+
O
3 i 1
W
−
W
,
W
+
W
3
mają część wspólną. W przypadku wartości tablicowych, niepewności pomiaru
§}¨C.
są zwykle
dużo mniejsze od niepewności
naszych pomiarów
1
§}¨C.
≪
3. W związku z tym wystar-
czy sprawdzić, czy wartość tablicowa
§}¨C.
zawiera się naszym przedziale
§}¨C.
∈ 1 −
, +
3. Jeśli tak jest, to możemy uznać nasz wynik za poprawny. W przeciwnym wypadku należy
sprawdzić, czy wartość tablicowa mieści się przedziale opartym na niepewności rozszerzonej
4
= 5 ∙
(dla
5 = 2 lub co najwyżej 5 = 3). Czyli musimy sprawdzić, czy
§}¨C.
∈
1 − 4 , + 4 3. Niespełnienie tego warunku z bardzo dużym prawdopodobieństwem oznacza,
że nasz wynik pomiaru jest niepoprawny. Przyczyną takiej sytuacji mogą być np. błędy systematycz-
ne, których nie zauważyliśmy, błędy w obliczeniach lub źle oszacowana niepewność pomiaru.
10.
Opracowywanie wyników pomiaru wielkości zależnych
10.1
Graficzna prezentacja wyników
Niekiedy dokonujemy pomiaru jakiejś wielkości fizycznej w funkcji innej wielkości, np. opór elek-
tryczny przewodnika w funkcji temperatury, natężenie oświetlenia w funkcji odległości od źródła
światła itp. Wyniki takich pomiarów powinniśmy przedstawić za pomocą wykresu. Graficzne przed-
stawienie wyników pomiarów wielkości zależnych pozwala m.in. na
•
Znajdowanie wartości, których nie zmierzyliśmy (poprzez graficzną interpolację lub ekstrapo-
lację).
•
Znajdowanie zależności funkcyjnej między wielkościami.
•
Łatwe wyłapywanie błędów.
•
Porównywanie wyników doświadczalnych z teorią.
•
Znajdowania różnego rodzaju parametrów (np. współczynnika nachylenia prostej), które wią-
żą się z (lub same są) wielkościami mierzonymi.
•
Przedstawianie złożonych zależności, których nie da się opisać za pomocą prostych związków
matematycznych, np. charakterystyki elementów elektronicznych.
W dobie komputerów rzadko kto rysuje jeszcze wykresy ręcznie na papierze milimetrowym, jed-
nak nawet używanie programów komputerowych do tworzenia wykresów nie zwalnia nas z obowiąz-
ku stosowania zasad rysowania wykresów, zwłaszcza w przypadku używania programów, w których
użytkownik sam decyduje o wielu elementach wykresu. Te zasady można ująć w następujących punk-
tach:
•
Wykres musi mieć opis (tytuł), który wyjaśnia, co ten wykres przedstawia.
•
Każda z osi wykresu musi być opisana. W opisie znajduje się nazwa lub symbol zmiennej,
której oś dotyczy oraz jednostka, w której oś jest wyskalowana.
•
Należy odpowiednio dobrać skale na osiach oraz początek układu współrzędnych tak, aby
wykres pokrywał znaczną część kartki w obu kierunkach (osie układu współrzędnych nie
muszą na wykresie zaczynać się od zera).
Wprowadzenie do metod opracowywania danych pomiarowych
35
•
Na osiach nanosimy skalę w postaci równooddalonych opisanych kresek odpowiadają-
cych czytelnym wartościom (np. 1, 2, 5 itd., a nie np. 1,24; 2,48; 3,62 itd.).
•
Nie nanosimy na osiach kresek odpowiadających współrzędnym punktów pomiarowych!
•
Punkty pomiarowe nanosimy w postaci wyraźnych znaków graficznych, takich jak krzyży-
ki, kółka, kwadraty itp. (punkt pomiarowy powinien leżeć w geometrycznym środku danej
figury).
•
Jeśli na jednym arkuszu rysujemy kilka wykresów, wówczas punkty należące do każdego z
nich oznaczamy w inny sposób (innym kolorem lub inną figurą).
•
Wokół punktów pomiarowych (wszystkich lub najbardziej charakterystycznych) nanosimy
prostokąty niepewności.
•
Ostatnią czynnością jest wykreślenie krzywej. Robimy to za pomocą przeźroczystych
krzywików i/lub linijek) w taki sposób, aby otrzymać gładką krzywą przechodząca przez
prostokąty niepewności. Liczby punktów pomiarowych leżących o obu stronach krzywej
powinny być zbliżone do siebie.
Przykład źle i poprawnie sporządzonego wykresu pokazano na rysunku 10.1.
(a)
(b)
Rys. 10.1. Przykład źle (a) i dobrze (b) narysowanego wykresu zależności oporu elektrycznego od
temperatury. Oba wykresy powstały na tych samych punktach pomiarowych.
10.2
Regresja liniowa
Załóżmy, że między mierzonymi wielkościami
, / występuje zależność linowa
/ =
+ .
10.1
Graficznym obrazem tej zależności jest prosta o współczynniku nachylenia przecinająca oś
rzędnych w punkcie . Parametry
, mają na ogół interpretację fizyczną. Na przykład zależność na-
pięcia na oporniku
4 od natężenia prądu , zgodnie z prawem Ohma ma postać 4 = « . W tym przy-
padku współczynnik kierunkowy prostej ma łatwą fizyczną interpretację – jest on równy oporowi
elektrycznemu opornika i, jeśli napięcie podamy w woltach, a prąd elektryczny w amperach, to
współczynnik kierunkowy naszej prostej będzie wielkością wyrażoną w omach. W większości przy-
padków interpretacja fizyczna parametrów a i b prostej jest bardziej złożona. Na przykład zależność
między niewielkim wydłużeniem drutu o długości początkowej i średnicy
• od wartości przyłożonej
do drutu siły
¬ ma zgodnie z prawem Hook’a postać

Obliczanie i wyrażanie niepewności pomiarowych
36
Δ =
4
A•
W
- ∙ ¬,
10.2
gdzie
- jest modułem Younga materiału, z którego wykonany jest drut. A zatem współczynnik kierun-
kowy prostej
† = ¬ jest równy
=
4
A•
W
-.
10.3
Wykonując pomiary długości i średnicy drutu oraz jego wydłużenia dla różnych sił, możemy po wy-
znaczeniu współczynnika obliczyć moduł Younga materiału, z którego wykonano drut
- =
4
A•
W
.
10.4
Parametry
, prostej dopasowującej punkty pomiarowe dwóch wielkości zależnych od siebie linio-
wo możemy oszacować metodą graficzną rysując na oko prostą przechodzącą możliwie blisko punk-
tów pomiarowych (wśród punktów pomiarowych nieleżących bezpośrednio na tej prostej, mniej wię-
cej połowa z nich powinna znajdować się nad, a połowa pod prostą). Do oszacowania niepewności
parametrów i musimy na wykres nanieść dwie skrajne proste oparte na wierzchołkach skrajnych
prostokątów błędów. Taka metoda da nam jednak bardzo niedokładne oszacowanie parametrów
prostej i ich niepewności. Znacznie lepszą metodą szacowania wartości parametrów funkcji dopaso-
wywanej do punktów pomiarowych jest tzw. metoda najmniejszych kwadratów. Zgodnie z tą metodą
najlepszymi parametrami naszej funkcji będą takie parametry, dla których suma kwadratów odchyleń
wartości tej funkcji i wartości zmierzonych będzie minimalna. W przypadku funkcji liniowej staramy
się tak dobrać parametry
, , aby zminimalizować funkcję
19
P , = K
L
+ − /
L
W
M
LNO
= minimum.
10.5
Spełnienie tego warunku dostajemy dla wartości
a, b wyliczonych według następujących wzorów
=
I ∑
L
/
L
M
LNO
− ∑
L
M
LNO
∑ /
L
M
LNO
I ∑
L
W
M
LNO
− 1∑
L
M
LNO
3
W
, = /2 − ̅,
10.6
Niepewności standardowe obu parametrów wyliczamy ze wzorów
= r
I
I − 2 ∙
∑ /
L
W
− ∑
L
/
L
M
LNO
M
LNO
− ∑ /
L
M
LNO
I ∑
L
W
M
LNO
− 1∑
L
M
LNO
3
W
,
=
∙ d
1
I ∙ K
L
W
M
LNO
.
10.7
19
Kryterium 8.5 daje nam najlepsze (w sensie metody najmniejszych kwadratów) oszacowanie parametrów
dopasowania przy założeniu, że wszystkie punkty pomiarowe są obarczone jednakowymi błędami przypadko-
wymi o rozkładzie Gaussa, a błędy systematyczne są małe w porównaniu z błędami przypadkowymi.
Wprowadzenie do metod opracowywania danych pomiarowych
37
W szczególnym przypadku zależność liniowa ma postać
/ = . W takim przypadku wzory na współ-
czynnik i jego niepewność standardowa przyjmują następującą postać
=
∑
L
/
L
M
LNO
∑
L
W
M
LNO
,
= r
1
I − 1 ∙
∑ /
L
W
− ∑
L
/
L
M
LNO
M
LNO
∑
L
W
M
LNO
.
10.8
W przypadku wielu funkcji nieliniowych jesteśmy w stanie dokonać transformacji, po których dosta-
niemy zależność liniową, do której będziemy mogli zastosować opisaną wyżej metodę. Na przykład
jeśli mamy zależność
/
=
W
+ ,
10.9
to po wprowadzeniu pomocniczej zmiennej
j
= 1
W
⁄ dostaniemy zależność liniową
/ j = j + .
10.10
Przy czym interesujące nas parametry
, nowej zależności są takie same jak naszej zależności pod-
stawowej. W innych sytuacjach otrzymana po transformacji zależność może mieć inne parametry,
które jednak będą w prosty sposób wiązać się z naszymi parametrami
, .
Musimy pamiętać, że metoda najmniejszych kwadratów wyliczy parametry dopasowania Gaussa
nawet w przypadku, gdy faktyczna zależność między mierzonymi wielkościami jest inna niż założona
przez nas. W takim przypadku krzywa „dopasowana” wcale nie musi przebiegać w pobliżu punktów
pomiarowych. Przykład takiej sytuacji pokazano na Rysunku 10.2 a.
(a)
(b)
Rys. 10.2. Przykład źle (a) i dobrze (b) dobranej zależności oporu elektrycznego termistora od
temperatury.
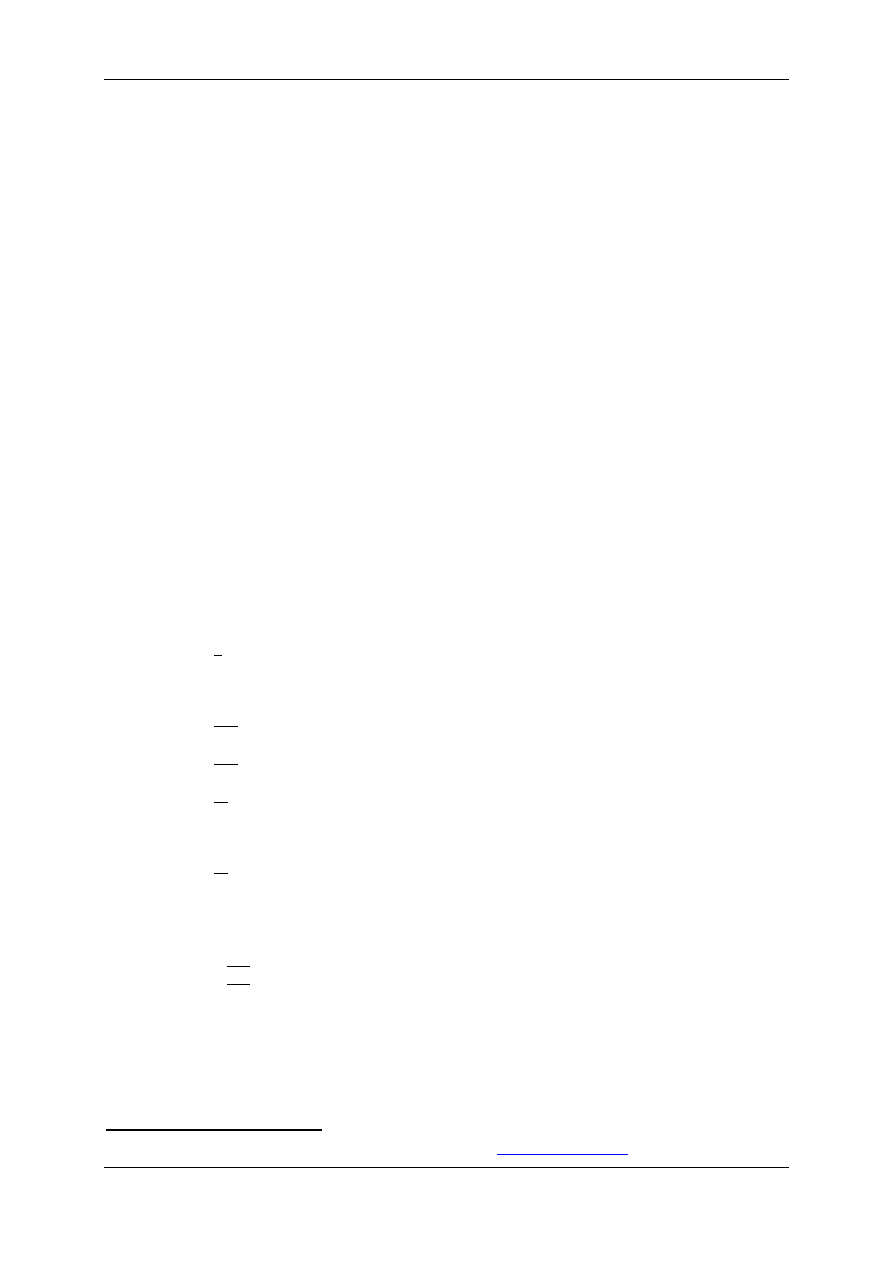
Obliczanie i wyrażanie niepewności pomiarowych
38
Dodatek A. Opis programu WykresLab
Na potrzeby prowadzonych przez Instytut Fizyki Politechniki Krakowskiej ćwiczeń laboratoryjnych
z fizyki powstał program o nazwie WykresLab. Studenci Politechniki Krakowskiej mogą korzystać z
niego na komputerach w pracowniach Instytutu Fizyki, a także instalować na swoich komputerach
prywatnych
20
. Praca w programie jest dość intuicyjna, dlatego opiszemy tu jedynie niektóre cechy
programu. Program służy do graficznej prezentacji wyników pomiaru wielkości zależnych od siebie i
znajdowania (metodą najmniejszych kwadratów) współczynników dopasowania oraz ich niepewności
standardowych. Obsługuje on większość zależności funkcyjnych, z jakimi spotykamy się w laborato-
rium studenckim. Na liście wyboru typu funkcji znajdziemy następujące pozycje:
1)
Brak (w przypadku wyboru tej pozycji wykres będzie zawierać tylko punkty pomiarowe).
2)
P
= • Ibx (możemy ją wybrać przedstawiając np. zależność oporu konstantanu od tem-
peratury)
3)
P
=
4)
P
=
+
5)
P
= S
}U
6)
P
= S
}U
+ •
7)
P
= ln / =
+ (czyli zależność typu 5 po zlinearyzowaniu)
8)
P
= S
}/U
9)
P
= ln / =
+ , = 1/ (czyli zależność typu 7 po zlinearyzowaniu)
10)
P
=
}
U
11)
P
= , = 1/ (czyli zależność typu 9 po zlinearyzowaniu)
12)
P
=
}
Uq¨
13)
P
=
}U
Uq¨
14)
P
=
}
U
G
15)
P
= , = 1/
W
(czyli zależność typu 13 po zlinearyzowaniu)
16)
P
=
}
U
G
+
17)
P
=
+ , = 1/
W
(czyli zależność typu 15 po zlinearyzowaniu)
18)
P
=
W
+
19)
P
= B
}
UT¨
20)
P
= 1 +
+
W
(zależność wykorzystywana w doświadczeniu z rezystorem termome-
trycznym PT100 w Pracowni miernictwa)
20
Program WykresLab można pobrać ze strony Instytutu Fizyki:
www.fizyka.pk.edu.pl
.

Wprowadzenie do metod opracowywania danych pomiarowych
39
21)
®
w = ˜ ›
¯ W
⁄ T®
k…
G
q ¯ W
⁄ T®
G
+
¯ W
⁄ q®
k…
G
q ¯ W
⁄ q®
G
œ; (patrz zadanie 3 ćwiczenia 17 Badanie pola magne-
tycznego za pomocą hallotronu).
22)
P
= ˜cos
W
, (np. ćw. 26)
23)
P
= , = cos
W
, (np. ćw. 26)
24)
Prawo Malusa we współrzędnych biegunowych (ćw. 26)
25)
=
sin
/
W
,
=
=>
°
U
√U
G
q¯
G
; (patrz ćw. 27: Dyfrakcja i interferencja świa-
tła lasera na szczelinach)
26)
P
= ˜
O
²
’
G
U
G
1U
G
T³
’
G
3
G
q²
’
G
U
G
+ ˜
W
²
G
G
U
G
1U
G
T³
G
G
3
G
q²
G
G
U
G
(Patrz ćw. 38: „Badanie absorpcji rezonansowej
światła w dielektrykach w zakresie widma widzialnego”).
27)
P
= ∑
z
z
M
zN
(funkcja wielomianowa, stopień wielomianu można zmieniać w zakresie
od 2 do 6. To dopasowanie ma zastosowanie w przypadku złożonych zależności funkcyjnych,
których postać teoretyczna nie jest znana, np. charakterystyka prądowo-napięciowa fotoko-
mórki w ćw. 21)
28)
5 w/j b5 S´ I (do punktów pomiarowych jest dopasowywana krzywa złożona z kawał-
ków wielomianów trzeciego stopnia przechodzących dokładnie przez punkty pomiarowe i
gładko zszywanych na granicach poszczególnych przedziałów. Ten typ funkcji w zasadzie nie
powinien być stosowany do opracowania graficznego ćwiczeń laboratoryjnych).
W programie można edytować kilka zestawów danych równocześnie. Będą się one znajdować na
kolejnych zakładkach o nazwach „Dane 1”, „Dane 2” itd. Do rysowania wykresu można wybrać
wszystkie lub tylko niektóre dane. Wyboru dokonujemy ustawiając
odpowiednio opcje wyboru „Dołącz do
wykresu” znajdujące się na każdej za-
kładce danych.
Część poleceń do pracy w edytorze danych jest ukrytych w menu
kontekstowym, jakie się otwiera w momencie kliknięcia prawym
klawiszem myszy w odpowiedni element w oknie edycyjnym da-
nych. Na przykład kliknięcie w tytuł zakładki otwiera menu pokaza-
ne na rysunku obok.
Znaczenie poszczególnych poleceń jest następujące:
•
„Wyczyść dane” – spowoduje usunięcie wprowadzonych liczb, ale zakładka pozostanie.
•
„Usuń dane” – spowoduje usunięcie danych wraz z całą zakładką, przy czym zostaniemy jesz-
cze poproszeni o potwierdzenie tej operacji.
•
„Usuń bez pytania” –zostanie usunięta cała zakładka bez konieczności potwierdzania.
•
„Usuń wszystko bez pytania” – usunięte zostaną wszystkie zakładki (bez konieczności po-
twierdzenia).

Obliczanie i wyrażanie niepewności pomiarowych
40
Kliknięcie prawym klawiszem myszy w tytuł kolumny X lub Y otwiera menu pokazane obok. Znaczenie
poszczególnych poleceń jest następujące:
•
„Wyczyść” – usuwa dane w danej kolumnie.
•
„Kopiuj” – kopiuje dane z kolumny do pamięci.
•
„Wytnij” – kopiuje dane z kolumny do pamięci i czyści kolumnę.
•
„Wklej” – wkleja dane zapamiętane wcześniej poleceniem „Ko-
piuj”.
•
„Zamień X z Y” – przenosi dane z kolumny X do kolumny Y, a dane
z Y do kolumny X.
•
„Ciąg arytmetyczny” – otwiera okno parametrów ciągu arytmetycznego (patrz niżej)
•
„Sortuj X” – sortuje dane w kolumnie X (cyklicznie rosnąco i malejąco).
•
„Sortuj Y” – sortuje dane w kolumnie Y (cyklicznie rosnąco i malejąco).
Polecenie „Ciąg arytmetyczny” pozwala wypełnić kolumnę kolejnymi wyrazami
ciągu arytmetycznego. W okienku podajemy początek ciągu (pierwszy wyraz),
koniec ciągu (ostatni wyraz) i krok ciągu. Możemy też zadecydować, czy dane
ciągu mają być dopisane do już wpisanych w danej kolumnie, czy też mają
zastąpić już wpisane.
Kliknięcie prawym klawiszem myszy w jakąś komórkę edycyjną w kolumnie X
lub Y otwiera menu pokazane niżej. Znaczenia poszczególnych poleceń są na-
stępujące:
•
„Przesuń komórki w dół” – przesuwa ciąg liczb w danej kolum-
nie w dół począwszy od klikniętej komórki pozostawiając klikniętą
komórkę pustą.
•
„Usuń komórkę” – usuwa liczbę w klikniętej komórce i prze-
suwa wszystkie liczby następujące po niej w tej kolumnie o jedną po-
zycję w górę.
•
„Wyczyść komórkę” – usuwa liczbę w klikniętej komórce.
Polecenia „Przesuń linię w dół”, „Usuń linię” i „Wyczyść linię” działają podobnie jak opisane wyżej,
tyle, że operacje te wykonywane są jednocześnie na komórkach w obu kolumnach.
Dane w komórkach możemy wpisywać używając jako separatora
dziesiętnego kropki lub przecinka (dowolnie). Można też wpro-
wadzać liczby w postaci typu 10,5E6 lub 10,5E+6 lub 10,5E-6.
Jednak zamiast wprowadzać liczby w takim formacie wygodniej jest skorzystać z przelicznika (patrz
rysunek obok). Każda kolumna ma osobny przelicznik. W zależności od ustawienia przycisków radio-
wych
„x”,
„/”,
kolumna
będzie
mnożona
przez
przelicznik
lub
dzielona.
Uwaga: po wprowadzeniu przelicznika, dane w kolumnie nie zmienią się. Efekt działania przelicznika
zobaczymy dopiero na wykresie.

Wprowadzenie do metod opracowywania danych pomiarowych
41
Po wydaniu polecenia „Wykres” na ekranie pokaże się graficzna
prezentacja wybranych danych. Możemy teraz opisać wykres
korzystając z okienka pokazanego obok.
Domyślnie drukowane są dwa identyczne wykresy (dla dwóch
osób wykonujących dane ćwiczenie) na jednej kartce, jeden pod
drugim, w orientacji pionowej, ale można wyłączyć drukowanie
dwóch wykresów na stronie.
Wpisane dane wraz z ustawieniami widocznymi na zakładkach edytora danych można zapisać na
dysku i wczytać w późniejszym czasie. Możliwe jest również zaimportowanie danych z pliku teksto-
wego, w którym dane zapisane są dwóch kolumnach oddzielonych znakiem tabulacji.

Obliczanie i wyrażanie niepewności pomiarowych
42
Dodatek B. Przepis obliczania niepewności pomiarowych
1.
Obliczanie niepewności pomiarów bezpośrednich
1.1
Obliczanie niepewności standardowej metodą A
Załóżmy, że wykonaliśmy serię
I ≥ 5 pomiarów wielkości i otrzymaliśmy wyniki
O
,
W
, … ,
M
. Jako
estymatę
(oszacowanie) wartości wielkości mierzonej przyjmujemy średnią aryt-
metyczną wyników pomiaru:
̅ =
1
I K
L
M
LNO
.
Niepewność standardową wynikającą z zaobserwowanego rozrzutu statystycznego wyników pomiaru
liczymy ze wzoru
21
:
‡
= r
∑
L
− ̅
W
M
LNO
I I − 1
.
1.2
Obliczanie niepewności standardowej metodą B
1.2.1
Opis ogólny
a)
Oceniamy granice przedziału (granicznego), w których według naszej wiedzy mieszczą się ak-
tualne i ewentualne przyszłe wyniki pomiarów. Niech
Δ oznacza połowę szerokości prze-
działu granicznego.
b)
Środek przedziału granicznego jest (najczęściej) estymatą wartości wielkości mierzonej.
c)
Przyjmujemy uproszczony rozkład prawdopodobieństwa wyników pomiaru na przedziale
granicznym. Najczęściej jest to rozkład prostokątny lub trójkątny symetryczny, zależnie od sy-
tuacji. Rozkład prostokątny przyjmujemy, jeśli według nas każdy wynik pomiaru w przedziale
granicznym jest równie prawdopodobny, a rozkład trójkątny wtedy, gdy prawdopodobień-
stwo wyników w pobliżu środka przedziału jest największe i spada do zera w miarę zbliżania
się do granic przedziału.
d)
Dla rozkładu prostokątnego, niepewność standardowa wyznaczona metodą B wynosi
ˆ
=
Δ
√3
.
e)
Dla rozkładu trójkątnego, niepewność standardowa wyznaczona metodą B wynosi
ˆ
=
Δ
√6
.
21
Jest to estymata tzw. odchylenia standardowego średniej arytmetycznej.

Wprowadzenie do metod opracowywania danych pomiarowych
43
1.2.2
Obliczanie niepewności standardowej wynikającej z dokładności przyrządu pom-
iarowego
Proste analogowe przyrządy pomiarowe (np. przymiar kreskowy)
W tym przypadku szacujemy naszą zdolność odczytu wyniku pomiaru ze skali przyrządu, np.
1/2, 1/4, 1/5 najmniejszej działki przyrządu. Stanowi to jednocześnie połowę szerokości przedziału
granicznego. Następnie postępujemy jak opisano w punkcie 5.2.1.
Proste analogowe elektryczne przyrządy pomiarowe (np. woltomierz analogowy)
Na niepewność pomiaru składają się dwa czynniki: niepewność odczytu położenia wskazówki
i niepewność wynikająca z wzorcowania przyrządu przez producenta. Pierwszy wkład do niepewności
obliczamy tak jak opisano w poprzednim punkcie. Oznaczmy ten składnik niepewności przez
¶·¸¹¸
. Drugi obliczamy na podstawie znajomości tzw. klasy przyrządu
5 i zakresu pracy przyrządu
º. Niepewność standardową związaną z tym czynnikiem liczymy ze wzoru
zC}|}
=
5 ∙ º
100 ∙ √3
Oba wkłady do niepewności sumujemy zgodnie z regułą składana niepewności standardowych i osta-
tecznie niepewność pomiaru analogowym, elektrycznym przyrządem pomiarowym wynosi:
ˆ
= B
|z}C}
W
+
zC}|}
W
.
Cyfrowe przyrządy pomiarowe
Korzystając ze wzoru podanego przez producenta przyrządu, obliczamy połowę szerokości
przedziału granicznego. Wzór podawany przez producenta zależy od: funkcji przyrządu (np. pomiar
napięcia stałego DC V) i zakresu przyrządu w momencie pomiaru (np. 2000 mV). Wzór może mieć
postać:
± 0.05%rdg + 3dgt
lub
±0.5% of rdg ± 2D
Symbol rdg oznacza odczytaną z wyświetlacza wartość wielkości mierzonej. Symbol dgt lub D oznacza
rozdzielczość przyrządu, czyli wartość odpowiadającą ostatniej pozycji na wyświetlaczu. Rozdzielczość
przyrządu zależy od zakresu na jakim pracuje przyrząd w momencie pomiaru. Np. jeśli wyświetlacz
przyrządu może wyświetlać 4 cyfry, to na zakresie 2000 mV – dgt=1 mV, a jeśli może wyświetlać 5
cyfr, to na zakresie 2000 mV – dgt=0,1 mV).
Sposób wykorzystania wzorów producenta pokazuje poniższy przykład.
Wykonano pomiar cyfrowym miernikiem ustawionym na funkcję pomiaru oporności elektrycznej i
pracującym na zakresie 2000 Ω. Rozdzielczość przyrządu na tym zakresie wynosi 1 Ω. Z wyświetlacza
przyrządu odczytano wynik pomiaru: 1562 Ω. Załóżmy, że w warunkach wykonywania pomiaru wzór
na dokładność pomiaru podany przez producenta ma postać
±0.8% of rdg ± 2D. Wobec tego po-
łowa szerokości przedziału granicznego wynosi:
Δ« =
0,8
100 ∙ 1562 Ω + 2 ∙ 1 Ω ≈ 14,496 Ω.

Obliczanie i wyrażanie niepewności pomiarowych
44
Na przedziale granicznym zakładamy prostokątny prawdopodobieństwa, a zatem niepewność stan-
dardowa pomiaru oporności
« wynosi
« =
14,496 Ω
√3
≈ 8,4 Ω.
2.
Sumowanie składników niepewności
Jeżeli policzyliśmy już wszystkie składniki niepewności, to musimy je zsumować. Sumowanie
niepewności standardowych wykonujemy sumując kwadraty tych niepewności, a następnie pier-
wiastkując otrzymaną sumę. Jeśli np. obliczyliśmy metodą A niepewność
‡
uwzględniającą roz-
rzut statystyczny wartości mierzonych oraz metodą B, niepewność
ˆ
wynikającą z dokładności
użytego przyrządu i są to jedyne składniki niepewności, to ostatecznie niepewność standardowa po-
miaru wyniesie
= B
‡
W
+
ˆ
W
.
3.
Obliczanie niepewności pomiarów pośrednich
Niech wielkość fizyczna
¿, mierzona pośrednio, jest powiązana z innymi wielkościami fizycz-
nymi
O
,
W
, … ,
Œ
związkiem
¿ = P
O
,
W
, … ,
Œ
.
Wykonujemy pomiary wielkości
O
,
W
, … ,
Œ
znajdujemy estymaty ich wartości
O
,
W
, … ,
Œ
oraz
niepewności standardowe tych estymat
O
,
W
, …
Œ
.
Estymatę wartości wielkości
/ znajdujemy wstawiając do powyższego związku estymaty wartości
wielkości
O
,
W
, … ,
Œ
:
/2 = P ̅
O
, ̅
W
, … , ̅
Œ
.
Niepewność standardową pomiaru, nazywaną złożona niepewnością standardową wyliczamy ze wzo-
ru
22
:
0
/ = dK •
L
L W
Œ
LNO
,
gdzie
•
L
, są tzw. współczynnikami wrażliwości, które są równe
•
L
≡
•P
•
L
‘
U
’
,U
G
,…,
“
.
22
Zakładamy, że wszystkie wielkości
O
,
W
, … ,
Œ
są niezależne (nieskorelowane).
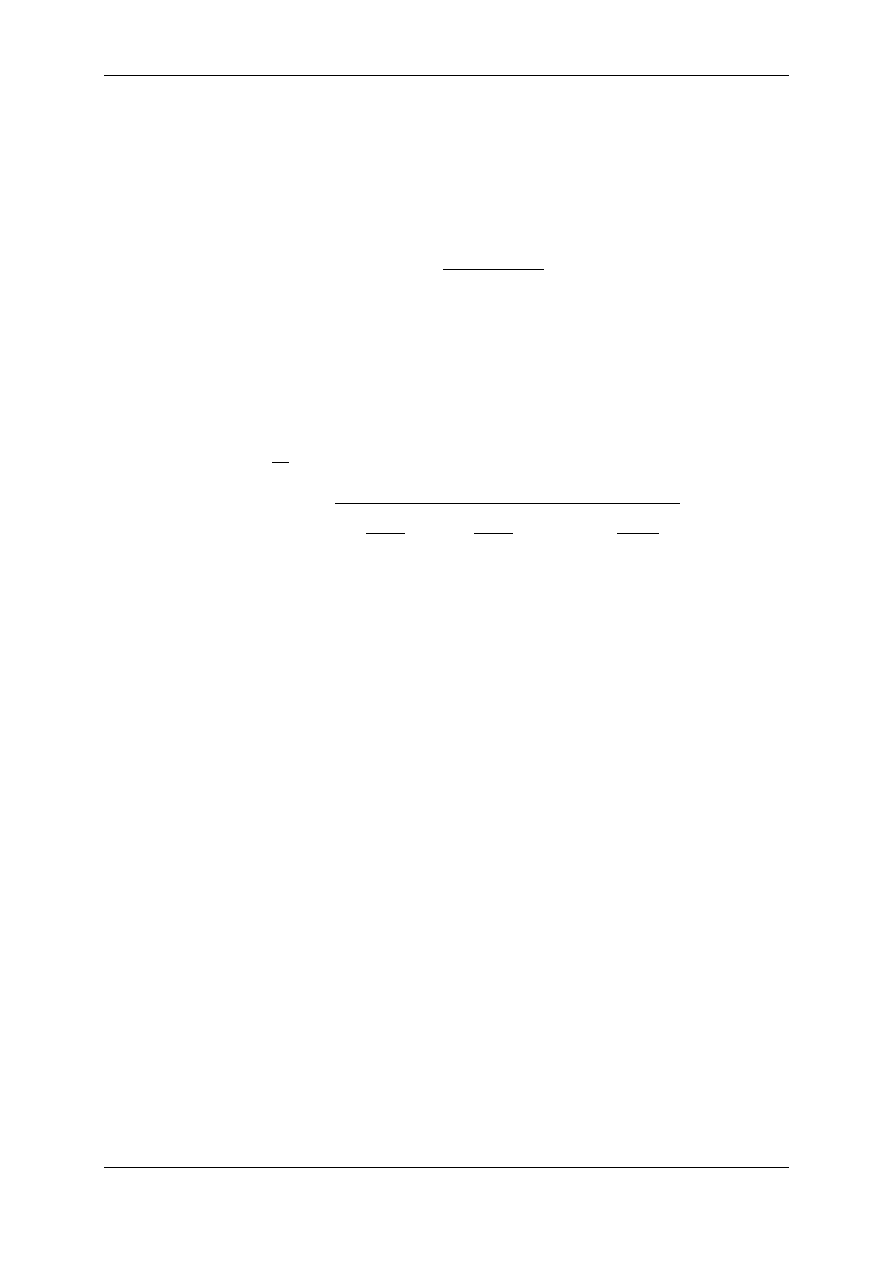
Wprowadzenie do metod opracowywania danych pomiarowych
45
Przypadki szczególne
a)
/ = P
O
,
W
, … ,
Œ
=
O O
+
W W
+
t t
+ ⋯ = K
L L
M
LNO
.
Wówczas
•
L
=
L
, a zatem
/ = dK
L
L W
Œ
LNO
,
b)
/ = P
O
,
W
, … ,
Œ
= ˜ ∙
O
’
∙
W
G
∙ … ∙
Œ
“
= ˜ ™
L
š
M
LNO
.
Wówczas
•
L
= /
š
U
š
, a zatem
/ = |/| ∙ r–j
O
(
O
)
O
—
W
+ –j
W
(
W
)
W
—
W
+ ⋯ + –j
Œ
(
Œ
)
Œ
—
W
.
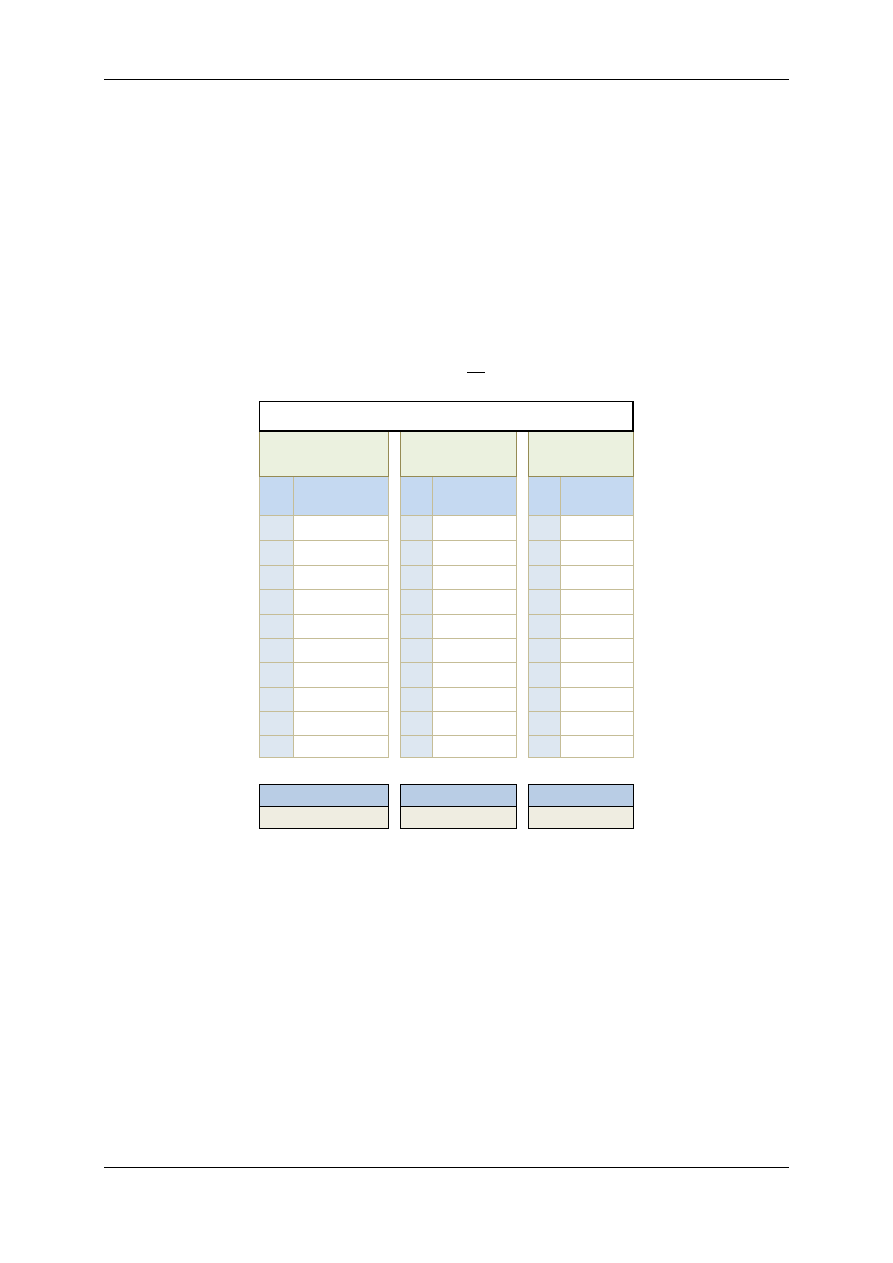
Obliczanie i wyrażanie niepewności pomiarowych
46
Dodatek C. Przykład opracowania danych pomiarowych po-
miaru wartości przyśpieszenia ziemskiego metodą wahadła
prostego.
Na rysunku C.1 przedstawiono dane pomiarowe zebrane w trakcie wykonywania ćwiczenia nr 1:
„Wyznaczanie wartości przyśpieszenie ziemskiego metodą wahadła prostego”. W celu wykonania
pomiaru pośredniego wartości przyśpieszenia ziemskiego
E mierzymy okres tzw. małych drgań
wahadła oraz jego długość . Jeśli podczas pomiarów będziemy wprawiać wahadło w drgania o wy-
starczająco małej amplitudzie (patrz analiza problemu w opisie ćwiczenia 1), to wartość przyśpiesze-
nia ziemskiego z dobrym przybliżeniem wyliczymy ze wzoru
E = 4A
W
W
.
Ćwiczenie 1. Dane pomiarowe
Czas 10. wahnięć
Długość nici
Średnica kulki
L.p.
x = 10 [s]
L.p.
ℎ [cm]
L.p.
[mm]
1.
21,8
1.
118,2
1.
19,00
2.
22,0
2.
118,2
2.
19,00
3.
21,6
3.
118,0
3.
19,00
4.
21,9
4.
4.
5.
22,1
5.
5.
6.
21,9
6.
6.
7.
21,9
7.
7.
8.
21,8
8.
8.
9.
22,0
9.
9.
10. 21,7
10.
10.
†x [s]
†ℎ[cm]
† [mm]
0,05
0,2
0,005
Rys. C.1 Przykładowe dane pomiarowe zebrane w trakcie wykonywania ćwiczenia nr 1: „Wyzna-
czanie wartości przyśpieszenie ziemskiego metodą wahadła prostego.
Uzasadnienie szacunków
Δx, Δℎ, Δ .
a)
Liczba pomiarów czasu 10. wahnięć wahadła upoważnia nas do policzenia niepewności me-
todą A. Ten wkład do niepewności uwzględnia rozrzut statystyczny wyników pomiarów. Po-
zostaje nam oszacowanie wkładu do niepewności uwzględniającego dokładność przyrządu
pomiarowego. Przyrządem pomiarowym był stoper o dokładności 0,1 s. Zasada działania tego
stopera (zakładając, że przyrząd jest sprawny technicznie) pozwala nam przyjąć, że odczytany
ze stopera czas nie różni się od rzeczywistego o więcej niż
0,1 s. Stąd przyjęta przez nas poło-
wa szerokości przedziału granicznego
Δx = 0,05 s.
UWAGA: Należy zwrócić uwagę, że pisząc w poprzednim zdaniu o czasie rzeczywistym, mamy
na myśli czas pomiędzy momentem włączenia i wyłączenia stopera, co nie koniecznie musi

Wprowadzenie do metod opracowywania danych pomiarowych
47
oznaczać faktyczny czas 10. wahnięć, gdyż względy subiektywnej oceny doboru momentów
startu i zakończenia pomiaru, a także czas reakcji obserwatora sprawiają, że często mierzony
czas nie odpowiada czasowi wymaganej liczby wahnięć (nie chodzi tu o zwykłe pomyłki typu
zmierzenia czasu 9. zamiast 10. wahnięć).
b)
Długość nici zmierzona była trzykrotnie, przy czym jeden z wyników różnił się o 0,2 cm od po-
zostałych. Liczba pomiarów jest za mała, żeby rozrzut statystyczny wyników oszacować me-
todą A. Gdyby zaobserwowany w serii 3. pomiarów rozrzut był duży, należałoby zwiększyć
liczbę pomiarów, aby móc zastosować metodę A. W naszej sytuacji możemy ograniczyć się do
metody B. Przedział graniczny powinien obejmować wszystkie pomiary (aktualne i ewentual-
nie przyszłe), więc musi mieć szerokość co najmniej 0,2 cm (nasza różnica między skrajnymi
wartościami). Bezpiecznie jest jednak założyć, że przedział graniczny jest szerszy od przypad-
ku zaobserwowanego przez nas. W przedstawionej tabeli przyjęto arbitralnie, że przedział
graniczny jest dwukrotnie szerszy od naszego przypadku, dlatego przyjęto, że połowa prze-
działu granicznego jest równa
Δℎ = 0,2 cm.
c)
Z tych samych powodów co w przypadku pomiaru długości nici, niepewność pomiaru średnicy
kulki musimy oszacować metodą B. Wszystkie wyniki pomiarów średnicy kulki były identycz-
ne, a zatem za połowę szerokości przedziału granicznego możemy przyjąć połowę najmniej-
szej działki przyrządu, w tym przypadku śruby mikrometrycznej o najmniejszej działce równej
0,01 mm. Stąd
Δ = 0,005 mm.
1.
Analiza pomiaru okresu drgań wahadła.
W celu wyznaczenia okresu drgań wahadła wykonano 10 pomiarów czasu
x trwania dziesięciu
wahnięć wahadła. Za wartość zmierzoną przyjmujemy średnią arytmetyczną wyników pomiarów,
która wynosi
x̅ = 102 = 21,870 s,
Ponieważ
= x 10
⁄ dostajemy
2 = x̅ 10
⁄ = 2,1870 s.
Wykonanie serii
10 pomiarów czasu x daje podstawę do wyliczenia niepewności standardowej meto-
dą A. Wyliczona w ten sposób niepewność standardowa (odchylenie standardowe średniej arytme-
tycznej) pomiaru czasu
x wynosi
Á
x ≈ 0,0473 s,
czyli niepewność standardowa pomiaru okresu jest równa
Á
=
Á
x /10 ≈ 0,00473 s.
Zgodnie z analizą dokonaną w poprzednim punkcie, połowa szerokości przedziału granicznego zwią-
zanego z wkładem do niepewności pochodzącym od przyrządu pomiarowego wynosi
Δx = 0,05 s.
Dodatkowo musimy założyć prostokątny rozkład gęstości prawdopodobieństwa (patrz. Uwaga w
punkcie 5.2.2). Wobec tego niepewność standardowa wyznaczona metodą B wynosi
Â
x =
0,05 s
√3
≈ 0,02887 s.
Stąd
Â
=
Â
x
10 ≈ 0,002887 s.

Obliczanie i wyrażanie niepewności pomiarowych
48
Sumując (zgodnie z regułą sumowania niepewności standardowych) niepewność obliczoną metodą A,
związaną ze stochastycznym rozrzutem wartości mierzonych oraz niepewność obliczoną metoda B
wynikającą z rozdzielczości stopera, dostajemy
0
= B
Á
W
+
Â
W
= 0,00554 s.
Po zaokrągleniu niepewności (do dwóch cyfr znaczących) i średniego okresu (do tego samego miejsca
rozwinięcia dziesiętnego co niepewność) ostatecznie dostajemy
= 2,1870 55 s.
2.
Analiza pomiaru długości wahadła
Długość wahadła złożonego z kulki zawieszonej na lekkiej (w porównaniu z kulką) nici jest zdefi-
niowana jako odległość od punktu zawieszenia wahadła do środka ciężkości kulki. Pomiar tej odległo-
ści w naszych warunkach wymagałby określenia „na oko” położenia środka kulki. Aby uniknąć tego
problemu wykonujemy pomiar pośredni długości wahadła. Mierzymy długość
ℎ nici i średnicę kulki,
a długość wahadła wyliczamy ze wzoru
= ℎ + 2
⁄ .
2.1
Analiza pomiaru długości nici
Pomiar długości nici wymaga staranności i pewnej wprawy. Taśmy mierniczej nie da się przyłożyć
bezpośrednio do nici co powoduje, że niepewność związana z odczytem jest większa niż najmniejsza
działka taśmy mierniczej (1 mm). Dla starannie wykonanego pomiaru długości nici można przyjąć, że
szerokość przedziału granicznego jest nie większa niż
3 ÷ 5 mm, czyli połowa tego przedziału jest
równa
Δℎ = 1,5 ÷ 2,5 mm. Zgodnie z analizą dokonaną pod rysunkiem C.1 przyjęliśmy Δℎ =
0,2 cm = 2,0 mm. Ponieważ nie mamy żadnych informacji o możliwym rozkładzie gęstości prawdo-
podobieństwa wyników pomiarów załóżmy dla bezpieczeństwa rozkład prostokątny, czyli
ℎ =
Δℎ √3
⁄
≈ 0,155 cm. Średnia wartość wyników pomiaru długość nici wynosi
ℎ2 = 118,133 cm.
Ostatecznie wynik pomiaru długości nici możemy zapisać w postaci
ℎ = 118,13 16 cm.
2.2
Analiza pomiaru średnicy kulki
Pomiar średnicy kulki wykonano śrubą mikrometryczną. Śruba mikrometryczna pozwala na po-
miar z dokładnością rzędu
0,01 mm. Dokładność tego pomiaru jest o dwa rzędy wielkości lepsza od
dokładności pomiaru długości nici. Wobec tego niepewność pomiaru średnicy kulki praktycznie nie
będzie miała wpływu na niepewność pomiaru długości wahadła i można ją z góry pominąć, ale doko-
najmy analizy tego pomiaru, żebyśmy mogli poprawnie zapisać wynik tego pomiaru.
Zgodnie z analizą dokonaną pod rysunkiem C.1 przyjmujemy
Δ = 0,005 mm. Przyjmując trój-
kątny rozkład gęstości prawdopodobieństwa dostajemy niepewność standardową pomiaru średnicy
kulki
= Δ √6
⁄
≈ 0,00204 mm. Zapis pomiaru średnicy kulki w notacji skróconej wygląda na-
stępująco (zwróćmy uwagę na 4 zera zapisane po przecinku – są one tu obowiązkowe)

Wprowadzenie do metod opracowywania danych pomiarowych
49
Jeśli we wzorach, za pomocą których wyliczamy wartość wielkości mierzonej pośrednio znajdują
się stałe fizyczne lub matematyczne, to musimy użyć przybliżeń tych stałych zawierających co
najmniej o dwie cyfry znaczące więcej niż inne liczby występujące w tym wzorze.
= 19,0000 20 mm.
Możemy teraz wyliczyć długość wahadła (pamiętajmy o wpisaniu długości nici i średnicy kulki w tych
samym jednostkach)
̅ = ℎ2 + ̅ 2
⁄ = 119,0833 cm.
Złożoną niepewność standardową tego pomiaru wyliczymy ze wzoru
= B1 ℎ 3
W
+ 11 2
⁄
3
W
≈ 0,115 cm.
Jak już zauważyliśmy niepewność tego pomiaru jest praktycznie równa niepewności pomiaru długości
nici.
Ostatecznie długość wahadła wynosi
= 119,08 12 cm.
3.
Analiza pomiaru wartości przyśpieszenia ziemskiego
Wartość przyśpieszenia ziemskiego otrzymana w wyniku naszego pomiaru pośredniego wynosi
E̅ = 4A
W
̅
2
W
≈ 4 ∙ 3,141593
W
0,11908
2,1870
W
s
W
≈ 9,8291 m/s
W
.
Zwróćmy uwagę na przybliżenie liczby
A zastosowane w powyższych obliczeniach.
W naszym wzorze liczby wynikające z pomiarów znamy z dokładnością do 4 i 5 cyfr znaczących. Dla-
tego popularne przybliżenie liczby
A ≈ 3,14 byłoby za mało dokładne. Powinniśmy użyć przybliżenia
liczby
A z dokładnością do minimum 7 cyfr znaczących.
Zgodnie z prawem propagacji niepewności, niepewność standardowa pomiaru pośredniego
E będzie
dana wzorem (patrz rozdz. 6, w szczególności przykłady 2 i 5)
E = E̅ ∙ r– ̅ —
W
+ –−2 ∙ 2 —
W
,
czyli
E = 9,8291
m
s
W
r›
0,12
119,08œ
W
+ ›
2 ∙ 0,0055
2,1870 œ
W
≈ 0,0507
m
s
W
.
Ostatecznie dostajemy
E = 9,829 51
m
s
W
.
Wynik ten wyznacza nam tzw. przedział objęcia o granicach
9,829
Ã
¶
G
− 0,051
Ã
¶
G
= 9,778
Ã
¶
G
i
9,829
Ã
¶
G
+ 0,051
Ã
¶
G
= 9,880
Ã
¶
G
, czyli
9,778, 9,880
Ã
¶
G
. Tablicowa wartość przyśpieszenia ziemskiego
dla Krakowa wynosi
E
§}¨.
= 9,81054 m/s
W
. Wartość ta mieści się w wyznaczonym przez nas prze-
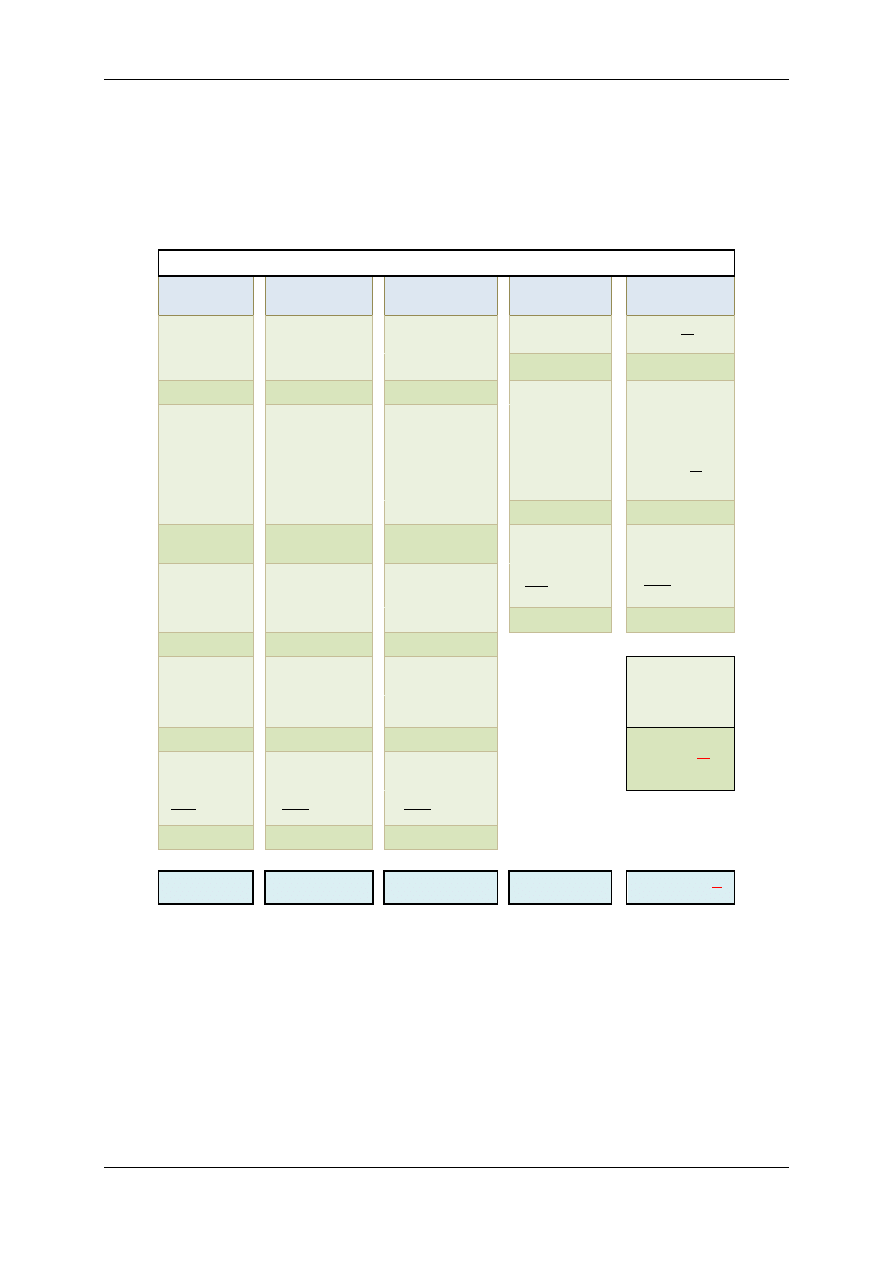
Obliczanie i wyrażanie niepewności pomiarowych
50
dziale, więc w sensie teorii pomiarów nasz wynik pomiaru możemy uznać za zgodny z wynikiem tabli-
cowym z prawdopodobieństwem ok. 0,7.
Obliczenia najwygodniej jest przeprowadzać przy użyciu jakiegoś programu kalkulacyjnego. Rysu-
nek C.2 przedstawia widok arkusza obliczeniowego w programie MS Excel utworzonego dla omówio-
nego w tym rozdziale przykładu.
Ćwiczenie 1. Arkusz obliczeniowy
Okres drgań
wahadła
Długość nici
Średnica kulki
Długość wahadła
Przyspieszenie
ziemskie
Średnia war-
tość okresu
Średnia długość
nici
Średnia długość
nitki
[cm]
E Ä
m
s
W
Å
T
śr.
[s]
h
śr.
[cm]
d
śr.
[mm]
119,0833
9,8291
2,18700
118,133
19,0000
niepewność
liczonametodą
A
(jeśli liczba
pom.>4)
niepewność
liczona metodą A
(jeśli liczba
pom.>4)
niepewność liczo-
na metodą A
(jeśli liczba
pom.>4)
niepewność
złożona
cm
niepewność
złożona
E
m
s
W
‡
s
‡
ℎ cm
‡
mm
0,11547
0,0507
0,004726
0,0000
0,00000
niepewność
względna proc.
niepewność
względna proc.
niepewność
liczona metodą B
niepewność
liczona metodą B
niepewność
liczona metodą B
· 100 %
E
E ∙ 100 %
ˆ
s
ˆ
ℎ cm
ˆ
mm
0,10%
0,52%
0,002887
0,1155
0,00204
niepewność
złożona
niepewność
złożona
niepewność
złożona
Wartość tablicowa
g
Tab
dla Krakowa
s
ℎ cm
mm
0,00554
0,1155
0,00204
9,8105
m
s
W
niepewność
względna proc.
niepewność
względna proc.
niepewność
względna proc.
· 100 %
ℎ
ℎ · 100 %
· 100 %
0,25%
0,10%
0,011%
= 2,1870 55 s
ℎ = 118,13 12 cm
= 19,0000 20 mm
= 119,08 12 cm
E = 9,829 51
m
s
W
Rys. C.2 Widok arkusza kalkulacyjnego utworzonego w programie MS Excel na potrzeby analizy
danych przedstawionych na Rysunku C.1.
Gdyby wartość tablicowa nie mieściła się w wyznaczonym przez nas przedziale należałoby
sprawdzić, czy mieści się w przedziale wyliczonym na podstawie niepewności rozszerzonej. Negatyw-
ny wynik tego drugiego porównania sugerowałby, że podczas pomiaru lub obliczeń popełniono jakieś
błędy. W takim przypadku należy spróbować znaleźć błędy, które do tego doprowadziły. W szczegól-
ności możemy sprawdzić dwie hipotezy:
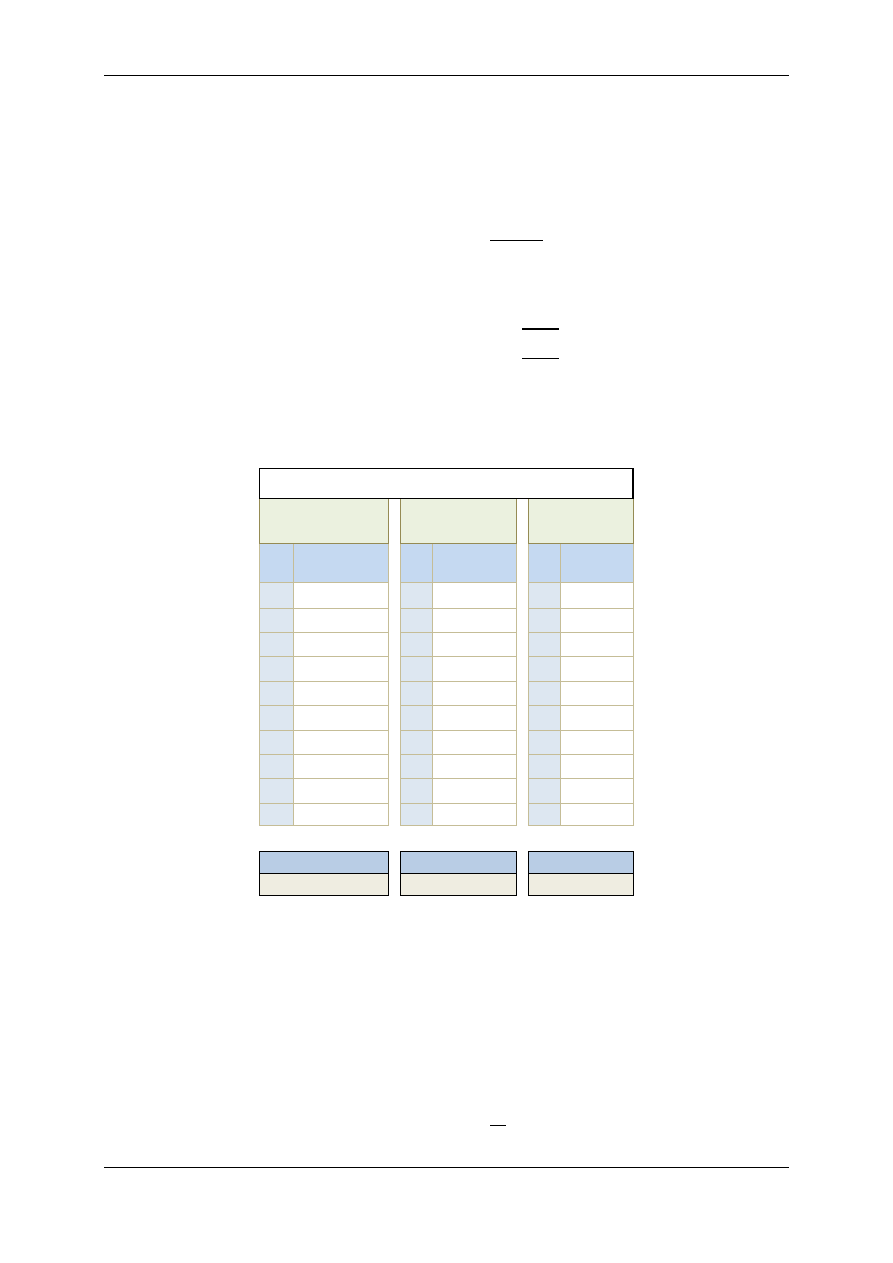
Wprowadzenie do metod opracowywania danych pomiarowych
51
a)
błąd pomiaru
E wynika z błędnego pomiaru długości wahadła.
b)
błąd pomiaru
E wynika z błędnego pomiaru okresu wahadła.
W pierwszym przypadku liczymy błąd
† , jaki musiałby być popełniony podczas pomiaru długości
wahadła, jeśli okres
2 zmierzony był dokładnie:
Δ = ̅ −
§ÇÈ….
= ̅ −
E
§}¨C
2
W
4A
W
.
W drugim przypadku liczymy błąd
† , jaki musiałby być popełniony podczas pomiaru okresu wahadła
jeśli długość
̅ zmierzona była dokładnie:
† = 2 −
§ÇÈ….
= 2 − 2Ar
̅
E
§}¨C.
.
4.
Przykład analizy wyników prowadzących do wartości niezgodnej z warto-
ścią tablicową
Ćwiczenie 1. Dane pomiarowe
Czas 10. wahnięć
Długość nici
Średnica kulki
L.p.
x = 10 [s]
L.p.
ℎ [cm]
L.p.
[mm]
1.
22,1
1.
118,2
1.
19,00
2.
21,8
2.
118,2
2.
19,00
3.
22,0
3.
118,0
3.
19,00
4.
21,8
4.
4.
5.
21,6
5.
5.
6.
21,9
6.
6.
7.
22,4
7.
7.
8.
22,2
8.
8.
9.
22,1
9.
9.
10. 21,9
10.
10.
†x [s]
†ℎ[cm]
† [mm]
0,05
0,1
0,005
Otrzymano następujące, końcowe wyniki pomiarów:
= 2,1980 78 s,
ℎ = 117,950 41 cm,
= 19,0000 20 mm,
= 118,900 41 cm.
Stąd dostajemy
E = 9,638 69
m
s
W
.

Obliczanie i wyrażanie niepewności pomiarowych
52
A zatem przedział objęcia jest równy
9,570; 9,707
m
s
W
.
Wartość tablicowa nie mieści się w tym przedziale. Przedział objęcia oparty na niepewności rozsze-
rzonej
4 E = 5 ∙ E ze współczynnikiem rozszerzenia 5 = 2 jest równy
9,501; 9,776
m
s
W
i nadal nie zawiera wartości tablicowej, chociaż jest przedziałem obejmującym ok. 95% rozkładu
prawdopodobieństwa wyników pomiaru wartości
E. Sprawdźmy zatem dwie hipotezy wymienione w
punkcie 3.
Według hipotezy a) popełniono błąd w pomiarze długości wahadła. Błąd ten musiałby wynosić:
Δ = −1,16 cm.
Jest mało prawdopodobne abyśmy pomylili się w pomiarze długości wahadła aż o 12 mm, chociaż
należałoby powtórzyć pomiar długości, aby zweryfikować tę hipotezę.
Według hipotezy b) popełniono błąd w pomiarze okresu wahadła. Błąd ten musiałby wynosić:
Δ = 0,011 s.
Oznacza to, że podczas pomiaru czasu trwania 10. wahnięć popełnialiśmy systematycznie błąd
Δx = 0,11 s.
Hipoteza b) wydaje się dość wiarygodna (patrz uwaga w punkcie a pod rysunkiem C.1). Należałoby
zatem przyjrzeć się naszemu sposobowi pomiaru, zauważyć nieprawidłowości w naszych pomiarach i
powtórzyć pomiary okresu wahadła z większą starannością. Można by również zwiększyć liczbę wah-
nięć z 10. do np. 30.

Wprowadzenie do metod opracowywania danych pomiarowych
53
Literatura
[1] Guide to the Expression of Uncertainty Measurement, Pierwsze wydanie 1993, poprawione w
1995. International Organization for Standarization 1993.
[2] Wyrażanie niepewności pomiaru. Przewodnik, Główny Urząd Miar 1999.
[3] A. Zięba, Natura niepewności pomiaru a jego nowa kodyfikacja. Postępy Fizyki 52, z. 5 (2001).
[4] H.Szydłowski, Międzynarodowe normy oceny niepewności pomiarów. Postępy Fizyki 51, z. 2
(2000).
[5] B.N.Taylor, C.E.Kuyatt, Guidelines for Evaluating and Expressing the Uncertainty of NIST Meas-
urement Results. Physics Laboratory. National Institute of Standards and Technology
Gaithersburg, 1994.
[6] J. Kurzyk, Obliczanie niepewności i wyrażanie niepewności pomiaru – wersja podstawowa. Doku-
ment wewnętrzny IFPK, 2013.
Wyszukiwarka
Podobne podstrony:
Niepewności pomiaru wersja rozszerzona
Niepewnosci pomiaru wersja podstawowa id 319237
Odzyskanie niepodległości przez Polskę wersja rozszerzona 2
NIEPEWNOŚĆ POMIARU
Wyk%c5%82ad Niepewno%c5%9b%c4%87 pomiaru
mierniki i niepewności pomiarowe
Błąd i niepewność pomiaru
podstawy analizy niepewności pomiarowych
FINANSE PUBLICZNE - 19.11.2013 (wersja rozszerzona), Wykłady(4)
Wyznaczanie niepewności pomiarów, PWr W9 Energetyka stopień inż, II Semestr, Podstawy metrologii i t
niepewnosci pomiarowe
3 Wyznaczanie niepewności pomiaru pośredniego
LOGOWANIE SIĘ WERSJA ROZSZERZONA
00 niepewność pomiaru
więcej podobnych podstron