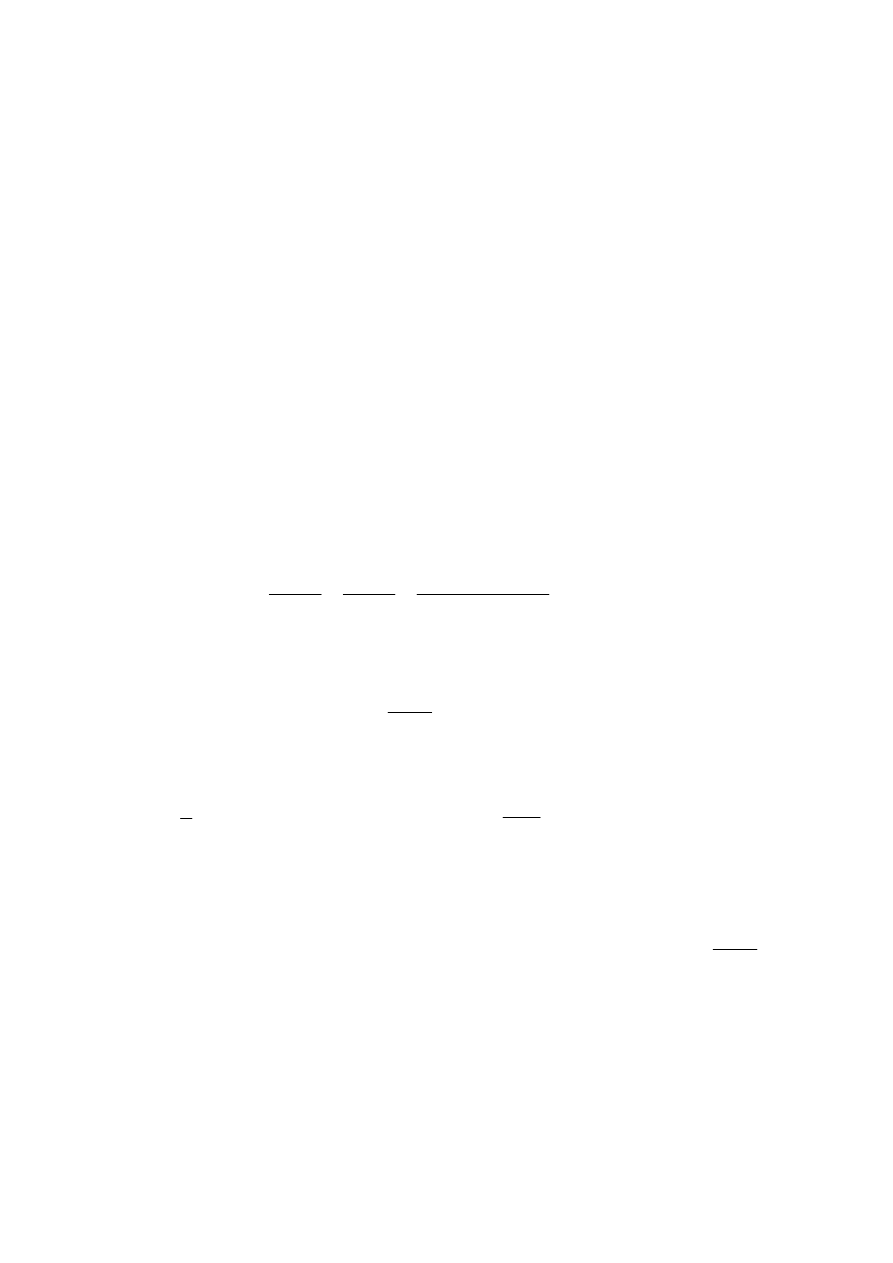
41

POCHODNA FUNKCJI

Informacje i zestawy

ć

wicze

ń

Niech b

ę

dzie dana funkcja f: A

∋

x

→

y = f(x)

∈

R, A

⊂

R. Niech

oznacza przyrost (dodatni lub ujemny ) liczony od punktu x, tak aby

Przyrostowi h zmiennej x odpowiada przyrost warto

ś

ci funkcji

Ilorazem ró

ż

nicowym

warto

ś

ci funkcji f(x) dla przyrostu h =

∆

x

(argumentu) zmiennej x nazywamy wyra

ż

enie

Ć

wiczenie 1.

Wyznaczy

ć

ilorazy ró

ż

nicowe

h

x

f

)

(

∆

dla funkcji:

1) f(x) = ax;

2) f(x) = ax

2

;

3) f(x) = ax

2

+ bx + c;

4)

x

a

x

f

=

)

(

;

5) f(x) = x;

6)

3

)

(

−

=

x

x

x

f

.

Ć

wiczenie 2.

Przyjmuj

ą

c dane z

Ć

wiczenia 1 wyznacz ilorazy ró

ż

nicowe

h

x

f

)

(

∆

w

punkcie x

o

, gdy

1) x

o

= -3;

2) x

o

= -1;

3) x

o

= 0,5 i h = 0,0001;

4) x

o

= 4 i h = 0,002;

5) x

o

= -2 i h = 0,009.

x

h

∆

=

A

x

x

h

x

∈

∆

+

=

+

).

(

)

(

)

(

)

(

)

(

x

f

x

x

f

x

f

h

x

f

x

f

−

∆

+

=

−

+

=

∆

h

x

f

h

x

f

h

x

f

x

x

f

)

(

)

(

)

(

)

(

−

+

=

∆

=

∆

∆

42

Ć

wiczenie 3.

Wyznaczy

ć

pochodne funkcji z

Ć

wiczenia 1.

Ć

wiczenie 4.

Uwzgl

ę

dniaj

ą

c dane z

Ć

wiczenia 1 (i ewentualnie z

Ć

wiczenia 3)

wyznaczy

ć

1) f'(-5);

2) f'(0);

3) f'(1, 2); 4) f'(4) (o ile istniej

ą

).

Pochodne funkcji elementarnych

1) y = ax,

y' = a;

2) y = c (c - stała),

y' = 0;

3) y = ax

2

,

y' = 2ax;

4) y = x

n

(n

∈

N),

y' = n

•

x

n-1

;

5) y = ,

y' = ;

6) y = x

α

dla x > 0 i

α

∈

R,

y' =

α

•

x

α

- 1

;

7) y = sin x,

y

'

= cos x;

8) y = cos x;

y' = -sin x;

Jeżeli istnieje granica skończona

R

x

g

h

x

f

h

x

f

h

∈

=

−

+

→

)

(

)

(

)

(

lim

0

, to granicę g(x)

nazywamy

pochodną funkcji

f

w punkcie

x i oznaczamy f

'

(x) lub

.

)

(

dx

x

df

x

1

2

1

x

−

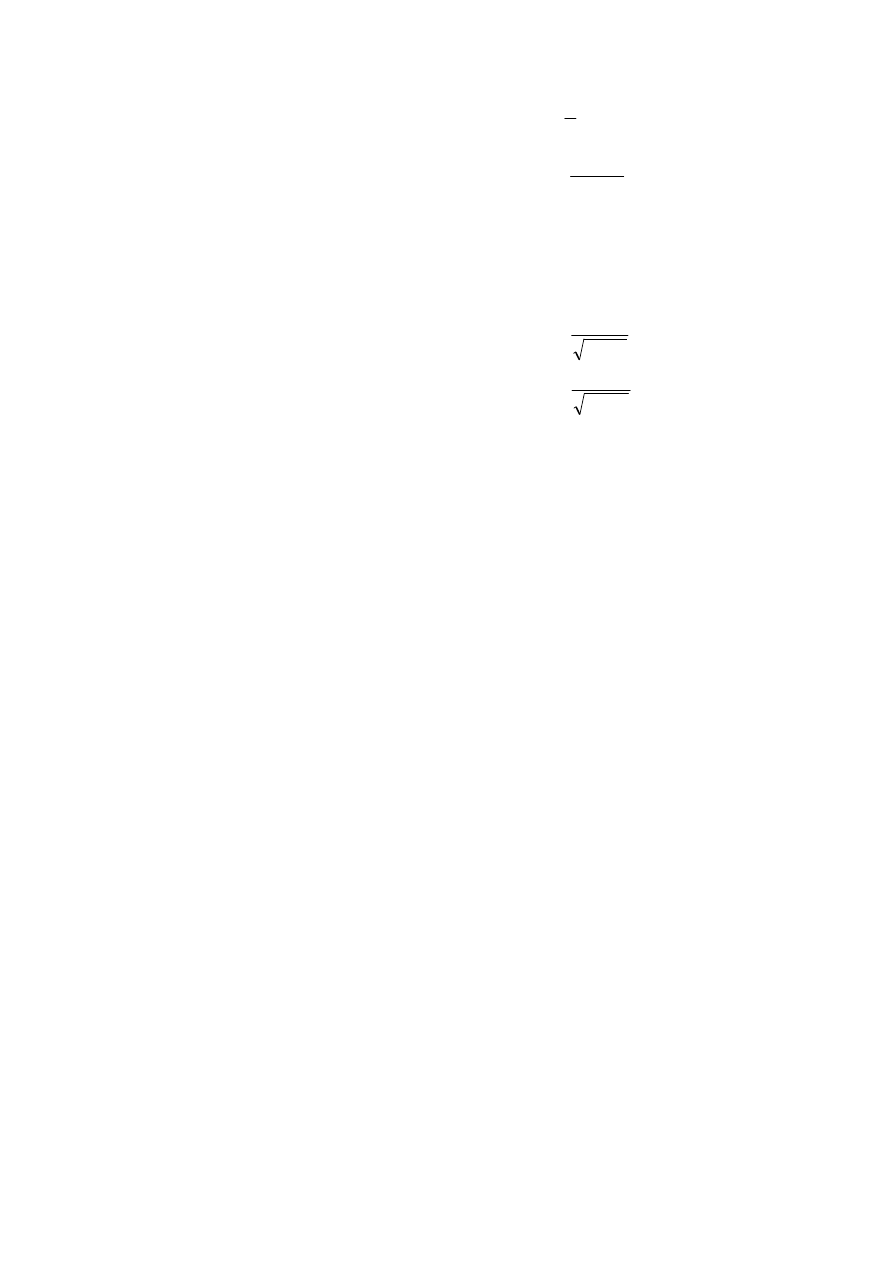
43

9) y = ln x dla x > 0,

y'

= ;

10) y = log

a

x dla x > 0 i a

∈

(0, 1)

∪

(1, +

∞

), y' = ;

11) y = e

x

,

y' = e

x

;

12) y = a

x

dla a > 0,

y' = a

x

ln a;

13) y = arcsin x dla -1 < x < 1,

y' =

14) y= arccos x dla -1 < x < 1,

y' = .

Ć

wiczenie 5.

Dane s

ą

funkcje x

→

f(x) i x

→

g(x). Zakładaj

ą

c,

ż

e istniej

ą

funkcje

x

→

f'(x) i x

→

g'(x) wyznaczy

ć

(f(x) + g(x))', (f(x) - g(x))', (f(x)

•

g(x))',

(f(x) : g(x))'.

Uwaga:

Poda

ć

odpowiednie warunki dla dziedziny funkcji danych oraz

ich pochodnych.

Ć

wiczenie 6.

Dane s

ą

funkcje x

→

y

→

f(x) = 2x - 1, x

→

y

→

g(x) = -3x + 2

(naszkicowa

ć

wykresy). Wyznaczy

ć

pochodne tych funkcji i naszkicowa

ć

ich wykresy.

x

1

a

x ln

1

•

;

1

1

2

x

−

2

1

1

x

−

−

44

Ć

wiczenie 7.

Dane s

ą

funkcje:

1) x

→

y = x

2

- 3x;

2) x

→

y = -x

2

+ 3;

3) x

→

y = x

2

+ x +7;

4) x

→

y

→

= -2x

2

+ 3x - 1.

Naszkicowa

ć

wykresy funkcji danych oraz ich pochodnych.

Ć

wiczenie 8.

Wyznaczy

ć

pochodne funkcji:

1) x

→

y

→

tg x = ;

2) x

→

y

→

ctg x = ;

3) x

→

y

→

cosec x = ; 4) x

→

y

→

sec x = .

Pochodne funkcji zło

ż

onej

Twierdzenie.

Niech b

ę

d

ą

dane funkcje x

→

y

→

f(x) i y

→

z

→

g( y) takie,

ż

e istnieje

funkcja

x

→

z = (g f)(x) = g(f(x)).

Je

ś

li istniej

ą

pochodne x

→

f

'

(x) i y

→

g

'

(y) dla y = f(x), to dla funkcji

zło

ż

onej

x

→

z = g(f(x)) istnieje pochodna x

→

z' = g'(f(x))

•

f'(x).

x

x

cos

sin

x

x

sin

cos

x

sin

1

x

cos

1

o

45

Ć

wiczenie 9.

Wyznaczy

ć

pochodne funkcji:

1) x

→

y = (x

2

+1)

5

,

2) x

→

y = 1 + x

2

,

3) x

→

y = A

•

sin(

ω

t +

ℵ

),

4) x

→

y = A

•

e

ax

.

Ć

wiczenie 10.

Wyznaczy

ć

pochodne funkcji:

1) x

→

y = f(x) = A

•

e

-ax

, 2) x

→

y = f(x) = dla -

∞

< x < +

∞

.

Pochodna funkcji odwrotnej

Niech b

ę

d

ą

dane: funkcja x

→

y = f(x) oraz funkcja do niej odwrotna

y

→

x = f

-1

(y).

Twierdzenie

Je

ż

eli istnieje pochodna x

→

f'(x) oraz f'(x)

≠

0, to istnieje pochodna

funkcji odwrotnej y

→

(f

-1

(y))' w punkcie y = f(x), przy czym

(f

-1

(y))' = 1 : f'(y) =

)

(

'

1

x

f

.

Ć

wiczenie 11.

Wyznaczy

ć

funkcje odwrotne do funkcji:

1) x

→

y = f(x) = ax + b, a

≠

0;

2) x

→

y = g(x) = x

3) x

→

y = a

x

dla a

∈

(0, 1)

∪

(1, +

∞

),

a nast

ę

pnie wyznaczy

ć

pochodne funkcji odwrotnych.

2

2

2

)

(

2

1

δ

δ

m

x

e

−

−

∏

46

Pochodna logarytmiczna

Niech b

ę

dzie dana funkcja f: A

∋

x

→

y = f(x)

∈

R, A

⊂

R, f(x)

≠

0.

Wyznaczy

ć

pochodn

ą

funkcji x

→

y = ln f(x). Funkcja x

→

y = ln f(x) jest

funkcja zło

ż

on

ą

, a wi

ę

c y' = (ln f(x))' =

)

(

)

(

'

)

(

'

)

(

1

x

f

x

f

x

f

x

f

=

•

, zatem (ln f(x))' =

)

(

)

(

'

x

f

x

f

. Wyra

ż

enie

)

(

)

(

'

x

f

x

f

nazywamy

pochodn

ą

logarytmiczn

ą

funkcji f(x).

Ć

wiczenie 12.

Dane s

ą

funkcje;

1) x

→

y = ln (x

2

- 3);

2) x

→

y = A

•

e

ax

.

Wyznaczy

ć

dziedziny tych funkcji oraz ich pochodne.

Pochodne wy

ż

szych rz

ę

dów

Ć

wiczenie 13.

Dla funkcji x

→

y = f(x) wyznaczy

ć

pochodne:

1) f(x) = ax + b,

f'(x), f''(x);

2) f(x) = ax

2

+ bx + c, f'(x), f''(x), f'''(x);

3) f(x) =

x

1

,

f'(x), f''(x), f

(n)

(x);

4) f(x) = sin x ,

f'(x), f''(x), f'''(x), f

(4)

(x);

5) f'(x) = e

x

,

f'(x), f''(x), f

(n)

(x).