Bardzo krótki kurs

różniczkowania

i całkowania

Rysunki i tablice: I.N. Bronsztejn, K.A. Siemiendiajew, Matematyka.
Poradnik encyklopedyczny, PWN, Warszawa 1968

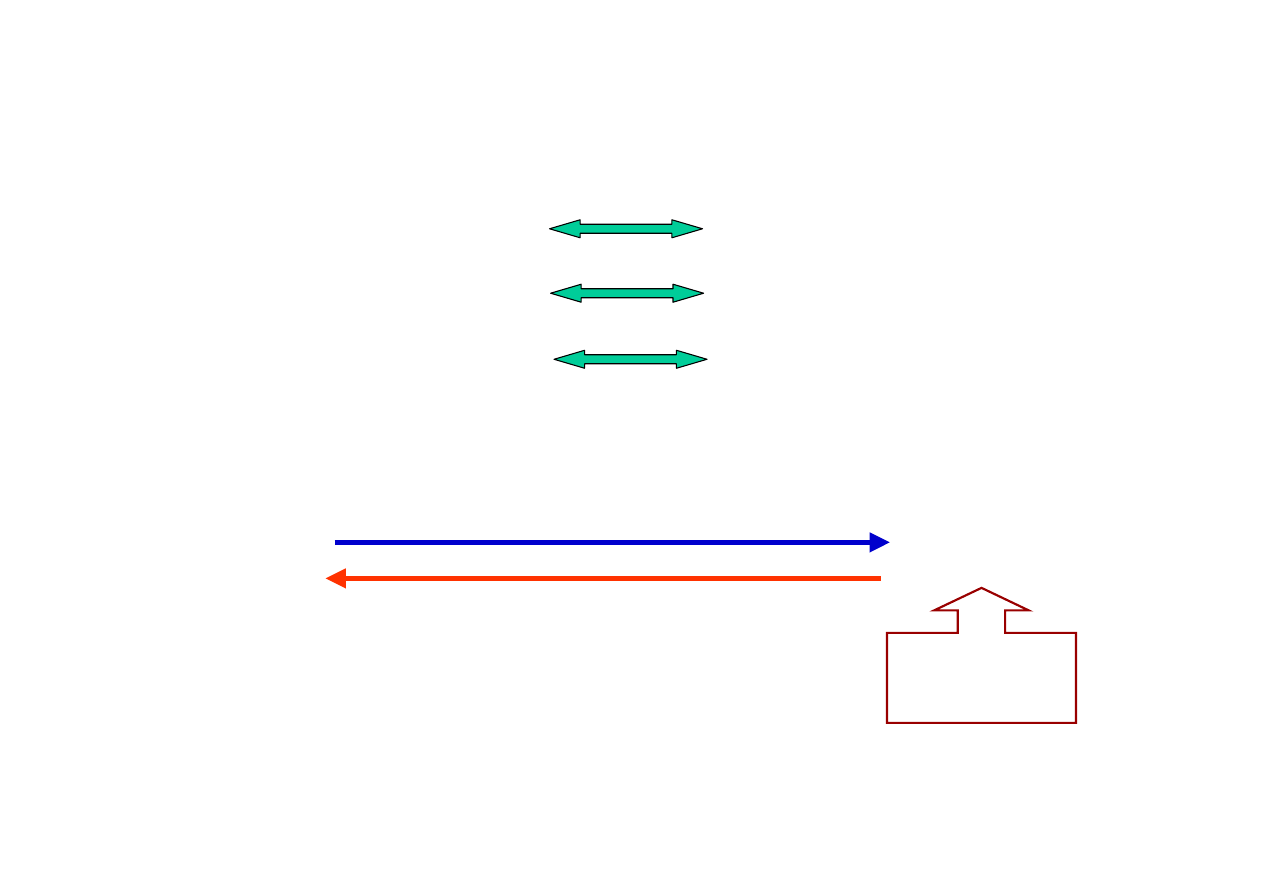
dodawanie odejmowanie

mnożenie dzielenie

różniczkowanie

całkowanie

f(x) f’(x)

różniczkowanie

całkowanie

Pochodna

funkcji f(x)

Technika różniczkowania

Technika różniczkowania

Pochodna sumy

Pochodna sumy

algebraicznej dwóch lub kilku funkcji (

u(x), v(x),

w(x), ...

) jest równa sumie algebraicznej pochodnych każdej z tych

funkcji:

(u+v+w+...)’ = u’+v’+w’+...

Stały czynnik

Stały czynnik

można wynosić przed znak pochodnej:

(cu)’ = cu’

Pochodna iloczynu

Pochodna iloczynu

dwóch lub kilku funkcji jest równa:

(uv)’=u’v+uv’

2

v

'

uv

'

vu

v

u

−−−−

====

′′′′













Pochodna funkcji złożonej

Pochodna funkcji złożonej

: jeżeli y=f(u) i u=

ϕϕϕϕ

(x),

to:

)

x

(

'

)

u

(

'

f

dx

dy

ϕϕϕϕ

====

Pochodną ilorazu

Pochodną ilorazu

oblicza się wg wzoru:

2

3))

(cos(2x

y

−

=

(...)

2

cos(...)

(2x–3)

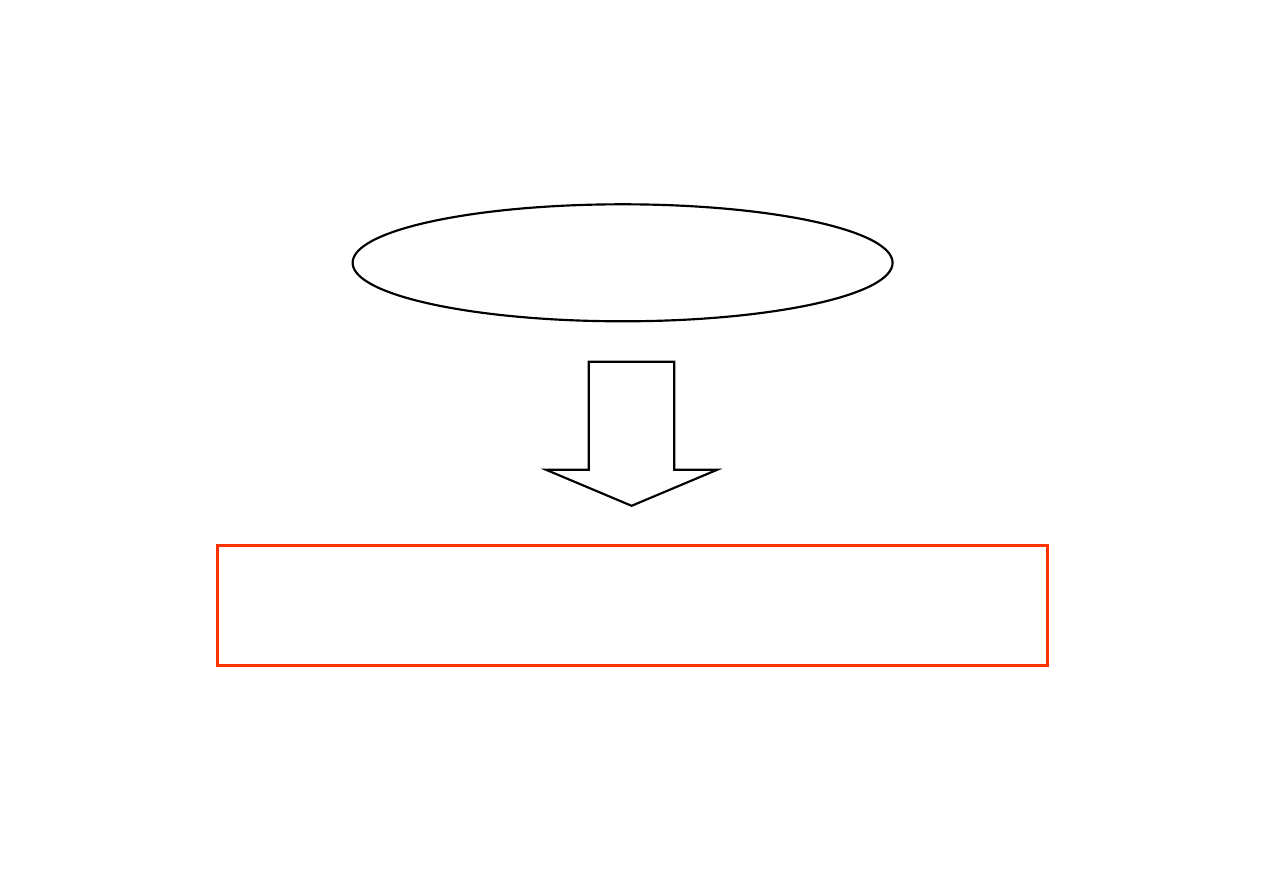
Jak obliczamy pochodne?

Pochodną funkcji złożonej sprowadzamy za

pomocą wcześniej poznanych wzorów do

kombinacji pochodnych

funkcji elementarnych

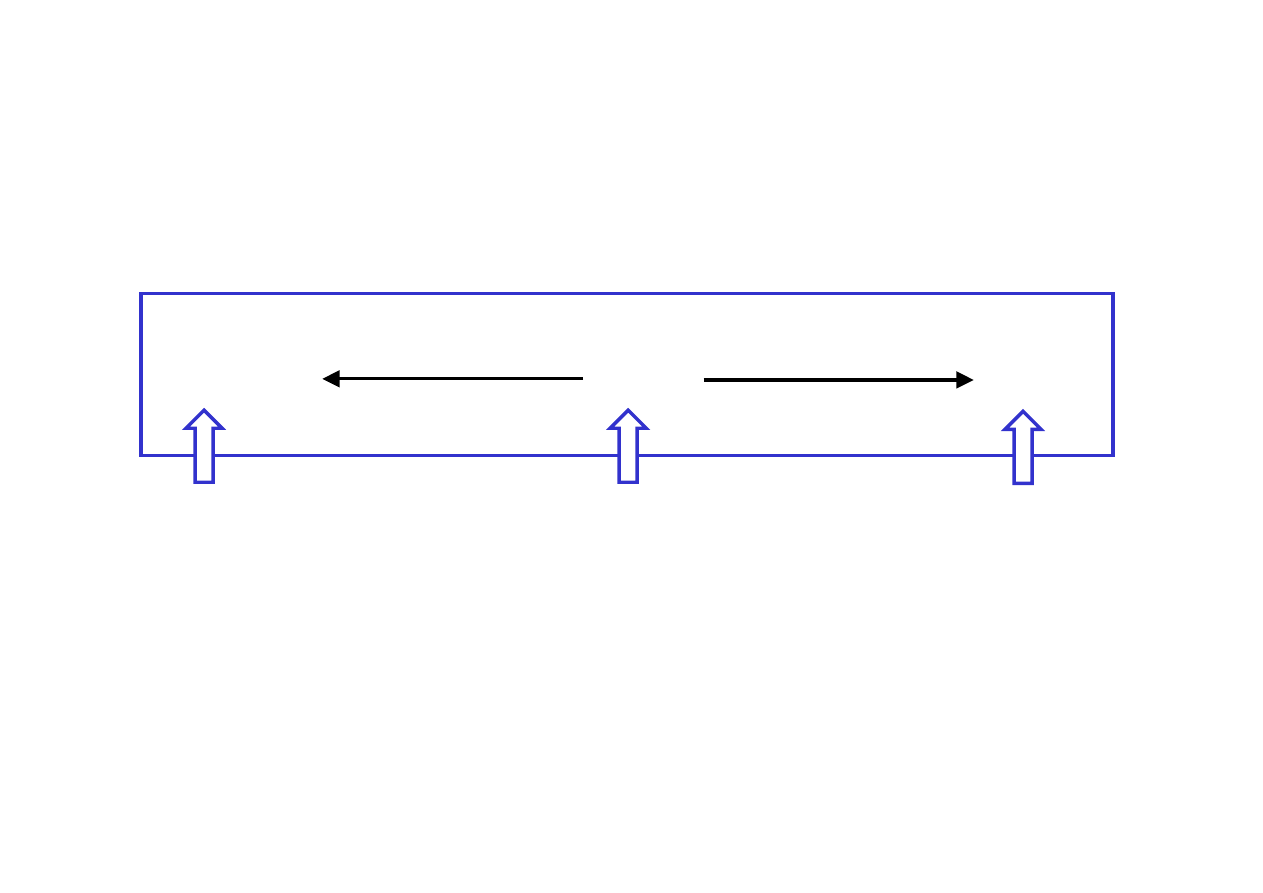
F(x)+C

F(x)+C

f(x)

f(x)

f’(x)

f’(x)

całkowanie

różniczkowanie

Funkcja
pierwotna
funkcji f(x)

Funkcja
f(x)

Pochodna
funkcji f(x)

F’(x)=f(x)

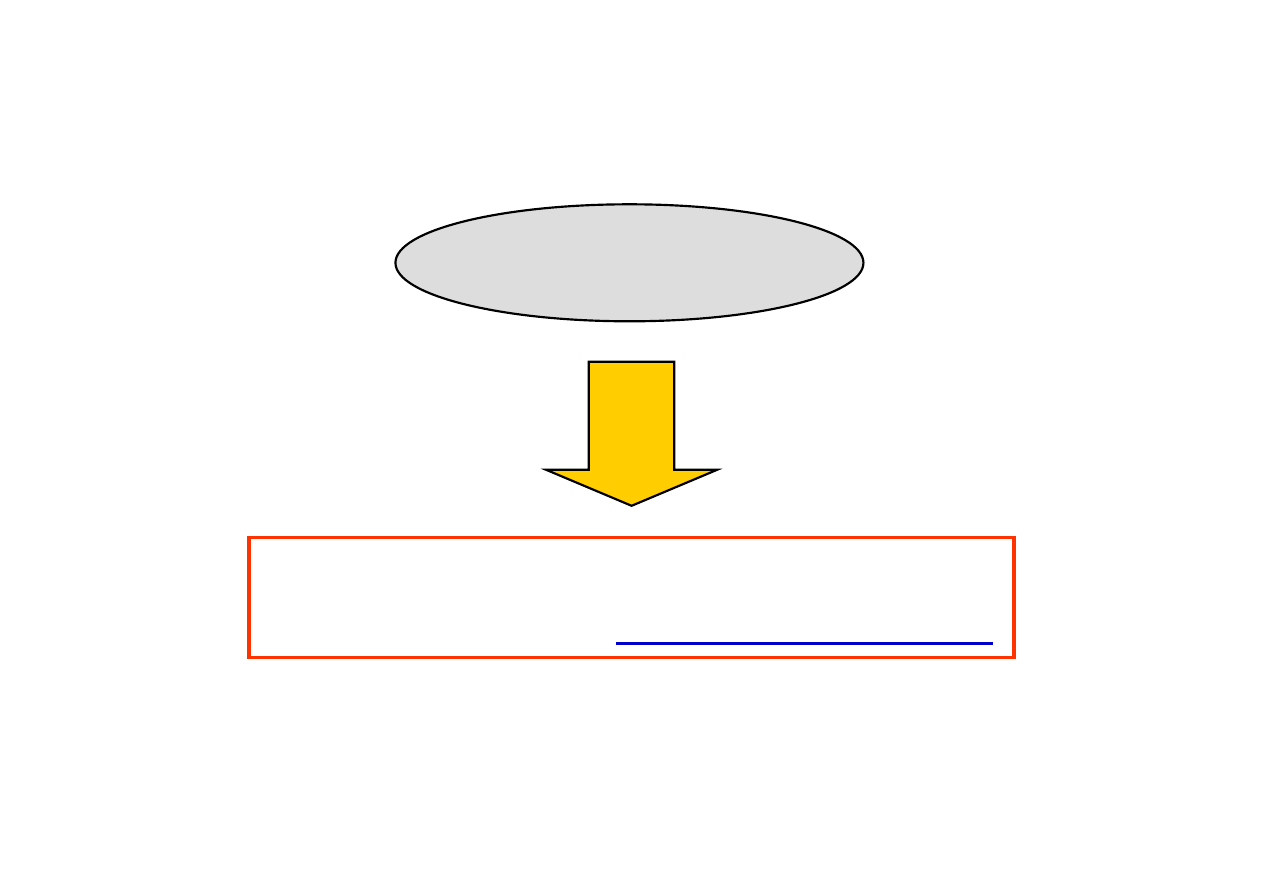
Całkę funkcji złożonej sprowadzamy, za

pomocą wzorów lub metodą podstawiania,

do kombinacji całek funkcji elementarnych

Jak obliczamy całki?

Nie zawsze jest to możliwe

→

→

→

→

całkowanie numeryczne

Podstawowe własności całki oznaczonej

Podstawowe własności całki oznaczonej

Całka o równych granicach całkowania jest równa 0:

∫∫∫∫

====

a

a

0

dx

)

x

(

f

Przy przestawianiu granic całkowania całka zmienia znak
na przeciwny:

∫∫∫∫

∫∫∫∫

−−−−

====

b

a

a

b

dx

)

x

(

f

dx

)

x

(

f

Rozkład całki

: dla dowolnych liczb a, b, c zachodzi związek:

∫∫∫∫

∫∫∫∫

∫∫∫∫

++++

====

b

a

c

a

b

c

dx

)

x

(

f

dx

)

x

(

f

dx

)

x

(

f

Całka sumy algebraicznej kilku funkcji

jest równa odpowiedniej sumie

algebraicznej całek tych funkcji:

∫∫∫∫

∫∫∫∫

∫∫∫∫

∫∫∫∫

ψ

ψ

ψ

ψ

−−−−

ϕϕϕϕ

++++

====

ψ

ψ

ψ

ψ

−−−−

ϕϕϕϕ

++++

b

a

b

a

b

a

b

a

dx

)

x

(

dx

)

x

(

dx

)

x

(

f

dx

)]

x

(

)

x

(

)

x

(

f

[

Stały czynnik

można wynieść przed znak całki:

∫∫∫∫

∫∫∫∫

====

b

a

b

a

dx

)

x

(

f

c

dx

)

x

(

cf

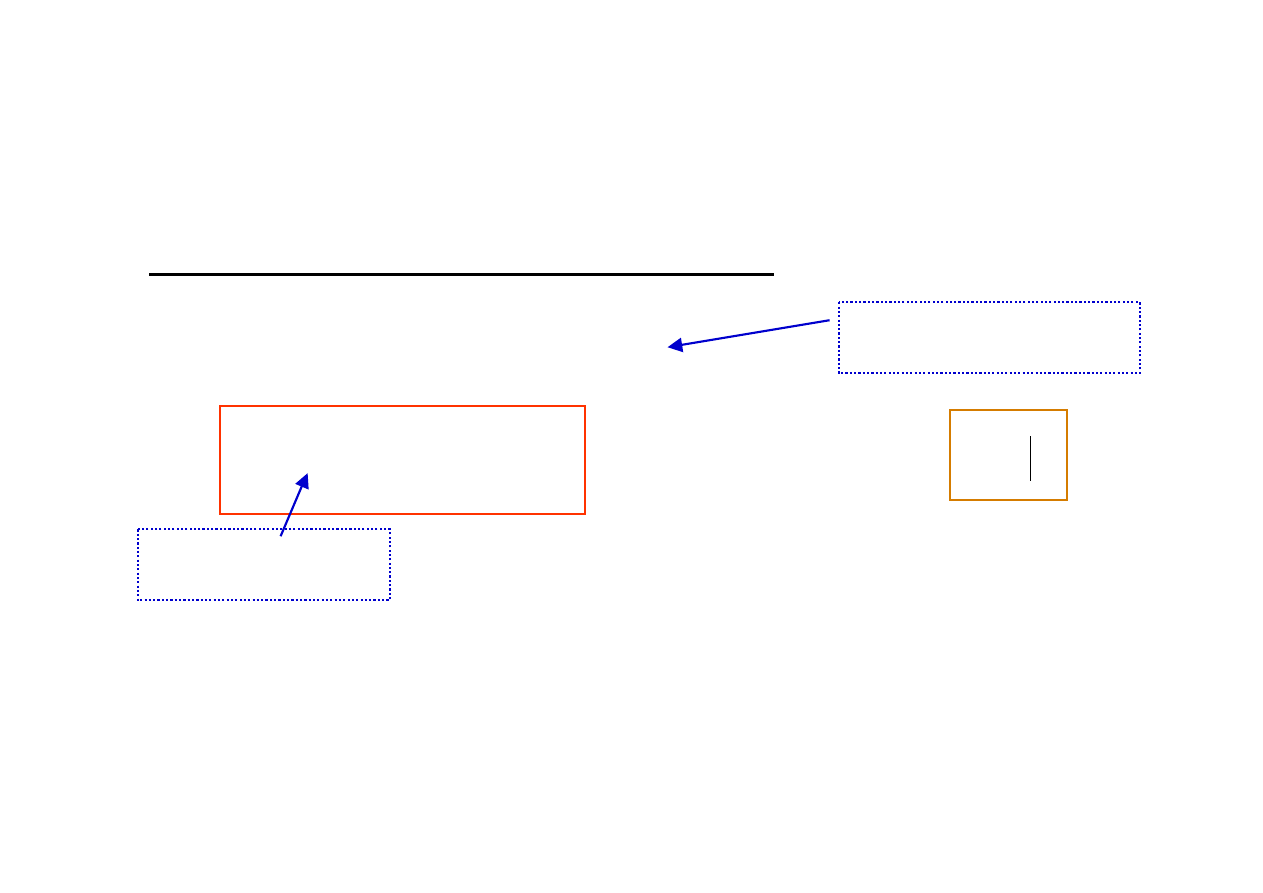
Obliczanie całek oznaczonych

Obliczanie całek oznaczonych

Stała całkowania C

przy podstawieniu granic całkowania znika i dlatego

można ją pominąć

Podstawowe twierdzenie rachunku całkowego (wyrażenie całki
oznaczonej przez nieoznaczoną). Jeżeli

to

∫∫∫∫

++++

====

C

)

x

(

F

dx

)

x

(

f

b

a

b

a

b
a

oznaczenie

)

x

(

F

lub

)]

x

(

F

[

)

a

(

F

)

b

(

F

dx

)

x

(

f

∫∫∫∫

























→

→

→

→









−−−−

====

Całka nieoznaczona
= funkcja

Całka oznaczona
= liczba

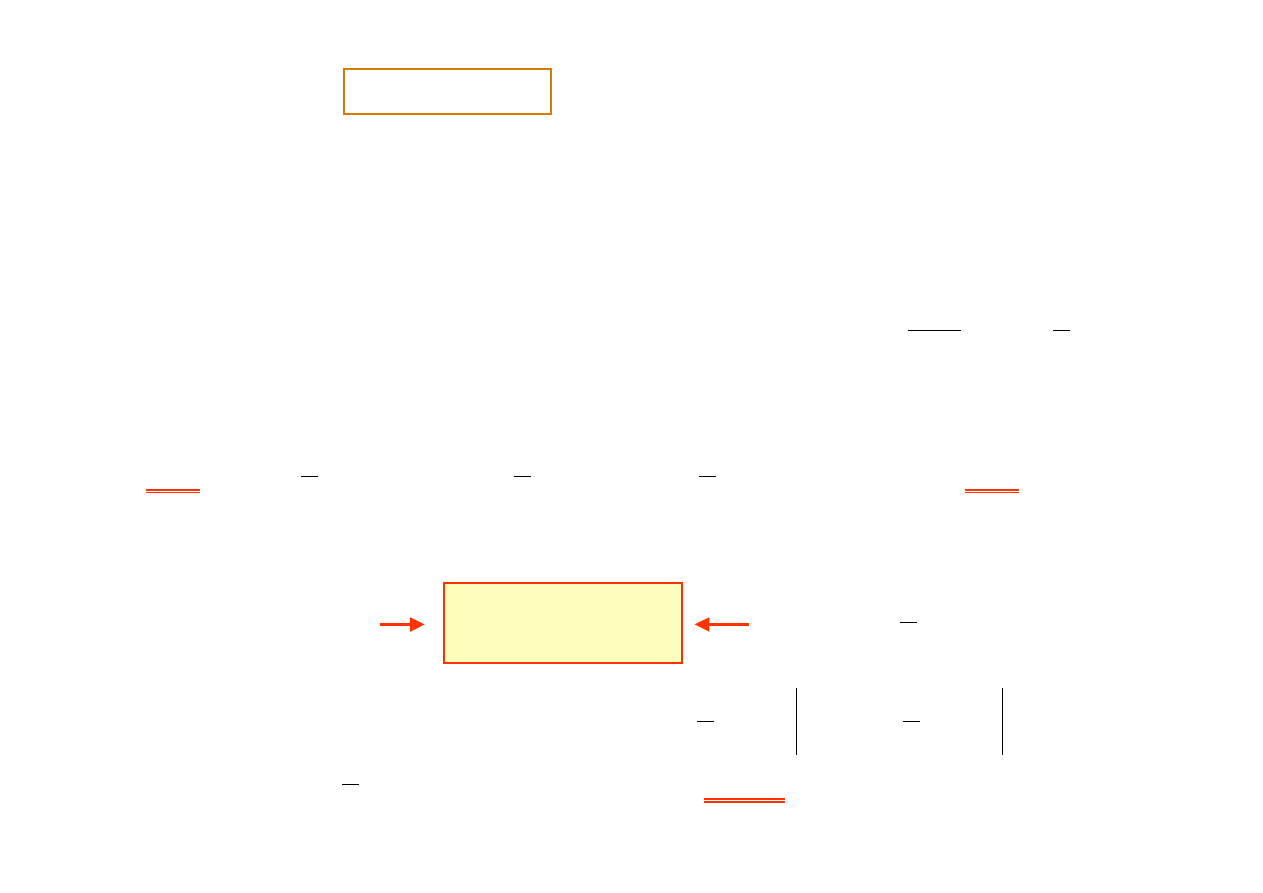
Mamy funkcję

f(x) = 5e

x

+3x

3

; obliczyć jej pochodną, całkę

nieoznaczoną oraz całkę oznaczoną w granicach {0, 1}

2

x

1

3

x

3

x

3

x

3

x

x

9

e

5

x

3

3

e

5

)'

x

(

3

)'

e

(

5

)'

x

3

(

)'

e

5

(

)'

x

3

e

5

(

)

x

(

'

f

++++

====

⋅⋅⋅⋅

++++

====

++++

====

++++

====

++++

====

−−−−

Pochodna:

Prz

ykł

ad

Całka nieoznaczona, czyli funkcja pierwotna F(x):

C

x

4

3

e

5

1

3

x

3

e

5

dx

x

3

dx

e

5

dx

)

x

3

(

dx

)

e

5

(

dx

)

x

3

e

5

(

4

x

1

3

x

3

x

3

x

3

x

++++

++++

====

++++

⋅⋅⋅⋅

++++

====

++++

====

++++

====

++++

++++

∫∫∫∫

∫∫∫∫

∫∫∫∫

∫∫∫∫

∫∫∫∫

Sprawdzamy, czy otrzymana funkcja jest rzeczywiście funkcją pierwotną:
F’(x) = f(x)

)

x

(

f

x

3

e

5

0

x

4

4

3

e

5

'

C

)'

x

4

3

(

)'

e

5

(

)'

C

x

4

3

e

5

(

)

x

(

'

F

3

x

1

4

x

4

x

4

x

====

++++

====

++++

⋅⋅⋅⋅

++++

====

++++

++++

====

++++

++++

====

−−−−

Całka oznaczona w granicach: a=0, b=1:

∫∫∫∫

−−−−

====

b

a

)

a

(

F

)

b

(

F

dx

)

x

(

f

f(x) = 5e

x

+3x

3

C

x

4

3

e

5

)

x

(

F

4

x

++++

++++

====

====

++++

++++

−−−−

++++

++++

====

−−−−

====

++++

====

∫∫∫∫

∫∫∫∫

0

4

x

1

1

0

1

0

4

x

3

x

)

C

x

4

3

e

5

(

)

C

x

4

3

e

5

(

)

0

(

F

)

1

(

F

dx

)

x

3

e

5

(

dx

)

x

(

f

25

.

9

5

75

.

0

e

5

C

0

5

C

4

3

e

5

====

−−−−

++++

====

−−−−

−−−−

−−−−

++++

++++

====

Liczba!

c.b.d.o.

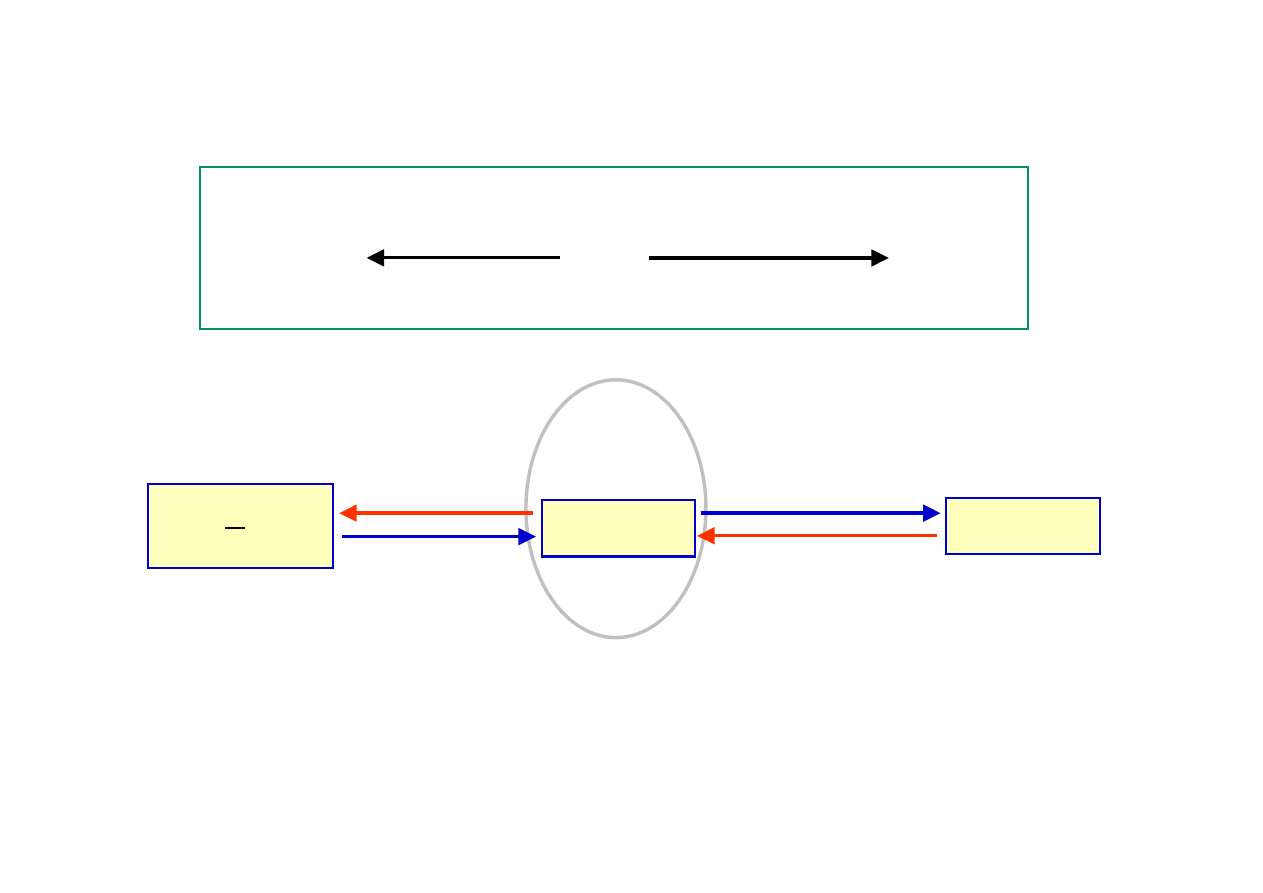
F(x)+C

F(x)+C

f(x)

f(x)

f’(x)

f’(x)

całkowanie

różniczkowanie

5e

x

+ 3x

3

C

x

4

3

e

5

4

x

++++

++++

5e

x

+ 9x

2

różniczkowanie

całkowanie

całkowanie

całkowanie

różniczkowanie

F(x) f(x)

f’(x)