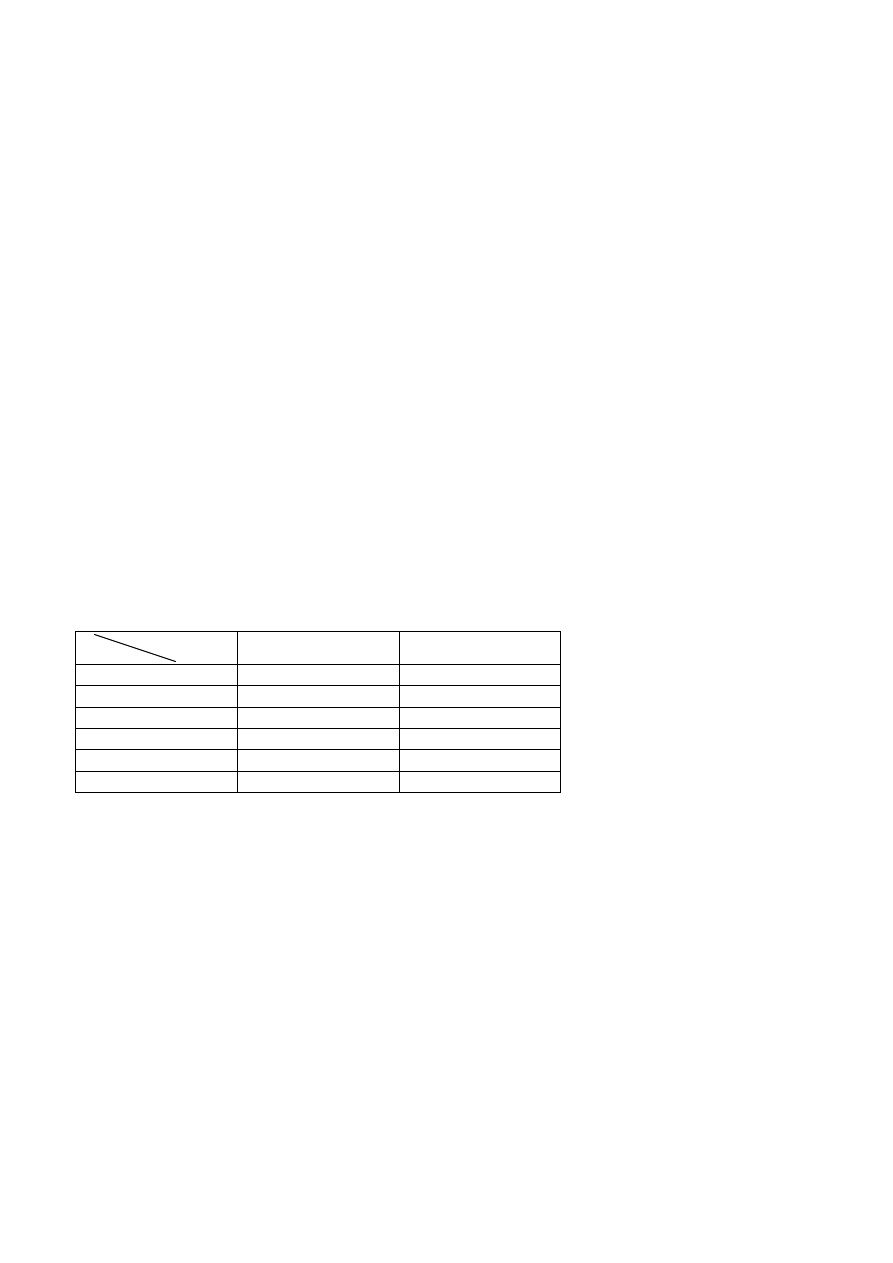
Zmienne losowe wielowymiarowe

Definicja:
Dana jest przestrzeń probabilistyczna (Ω, S, P ) i w tej przestrzeni n zmiennych losowych

n

X

X

X

,...,

,

2

1

. Uporządkowany układ n zmiennych losowych oznaczamy jako:

}

,...,

,

{

2

1

n

X

X

X

X

=

i

nazywamy n – wymiarową zmienną losową lub wektorem losowym X.

W ten sposób każdemu zdarzeniu elementarnemu

Ω

∈

ω

przyporządkowujemy układ n liczb

rzeczywistych, czyli punkt n – wymiarowej przestrzeni euklidesowej

n

ℜ

.

Przykład 1:
Wyobraźmy sobie doświadczenie, w czasie którego wykonujemy jednoczesny rzut kostką i monetą.
Wyniki rzutu kostką można uważać za zmienną losową :

1

X

- przyjmującą wartości 1, 2, ... , 6 z prawdopodobieństwem 1/6.

2

X

- przyjmującą wartości 0 –orzeł, 1 – reszka z prawdopodobieństwem ½.

W wyniku jednoczesnego rzutu kostką i monetą otrzymujemy 2 wartości. Mamy więc do czynienia ze

zmienną losową dwuwymiarową

)

,

(

2

1

X

X

, która może przyjąć jedną z 12 wartości:

(1,0), (1,1), (2,0), (2,1), (3,0), (3,1), (4,0), (4,1), (5,0), (5,1), (6,0), (6,1).

Jest sprawą intuicyjnie oczywistą, że wszystkie12 wartości zmiennej losowej

)

,

(

2

1

X

X

są równo

prawdopodobne. Czyli:

12

/

1

)

,

(

2

1

=

=

=

l

X

k

X

P

dla k = 1, ... , 6 ; l = 0, 1.

Tabelaryczny zapis tej dwuwymiarowej zmiennej losowej

)

,

(

2

1

X

X

:

1

X

2

X

0

1

1

1/12

1/12

2

1/12

1/12

3

1/12

1/12

4

1/12

1/12

5

1/12

1/12

6

1/12

1/12

Definicja:

Dystrybuantą zmiennej losowej n – wymiarowej

)

,...,

,

(

2

1

n

X

X

X

nazywamy funkcję:

)

,...,

,

(

2

1

n

x

x

x

F

=

)

,...,

,

(

2

2

1

1

n

n

x

X

x

X

x

X

P

<

<

<

Właściwości:

1.

)

,...,

,

(

∞

∞

∞

F

=

1

)

,...,

,

(

2

1

=

∞

<

∞

<

∞

<

n

X

X

X

P

2. Dystrybuanta jest funkcją lewostronnie ciągłą.

3.

0

)

,...,

,

,...,

,

(

1

,

1

2

1

=

∞

−

+

−

n

i

i

x

x

x

x

x

F

. Wynika to z tego, że zdarzenie polegające na tym, że

zmienna losowa

i

X

przyjmuje wartość mniejszą niż

∞

−

, jest zdarzeniem prawie niemożliwym

(prawdopodobieństwo równe zeru).
4. Jeżeli zbiór wartości dystrybuanty jest skończony lub przeliczalny, to zmienną losową n –
wymiarową nazywamy dyskretną lub typu skokowego.
Jeżeli dystrybuanta jest różniczkowalna ( w sensie klasycznym), to zmienną losową
wielowymiarową nazywamy ciągłą.

Definicja:
Funkcja gęstości prawdopodobieństwa wielowymiarowej zmiennej losowej ciągłej jest pochodną jej
dystrybuanty:

)

,...,

,

(

2

1

n

x

x

x

f

=

n

n

x

x

x

x

x

x

F

∂

∂

∂

∂

...

)

,...,

,

(

2

1

2

1

Własności funkcji gęstości prawdopodobieństwa:

1.

0

)

,...,

,

(

2

1

≥

n

x

x

x

f

2.

1

...

)

,...,

,

(

...

2

1

2

1

=

∫ ∫

∞

∞

−

∞

∞

−

n

n

dx

dx

dx

x

x

x

f

Momenty zmiennej losowej wielowymiarowej

Mamy zmienną losową n – wymiarową

)

,...,

,

(

2

1

n

X

X

X

. Zakładamy, że dla każdej z tych

zmiennych

i

X

( i = 1, 2, ... , n ) są określone momenty zwykłe.

Definicja:
Momenty mieszane rzędu r + s zmiennej losowej wielowymiarowej definiuje się następująco:

(

)

s

l

r

k

rs

kl

X

X

E

⋅

=

α

dla k, l = 1, 2, ... , n

Sumę r + s nazywamy rzędem momentu.

Definicja dla zmiennej losowej wielowymiarowej skokowej

i

X

( i = 1, 2, ... , n ) przyjmującej wartości

i

im

x

)

,...,

2

,

1

(

i

i

K

m

=

:

)

,

(

1

1

l

k

l

k

k

l

l

k

lm

l

km

k

s

lm

K

m

K

m

r

km

rs

kl

x

X

x

X

P

x

x

=

=

=

∑∑

=

=

α

Definicja dla zmiennej losowej wielowymiarowej ciągłej:

n

n

s

l

r

k

rs

kl

dx

dx

dx

x

x

x

f

x

x

...

)

,...,

,

(

...

2

1

2

1

∫ ∫

∞

∞

−

∞

∞

−

=

α

Momenty poszczególnych zmiennych losowych

i

X

można uważać za graniczne przypadki momentów

mieszanych, np.

k

kl

EX

=

10

α

- jest wartością oczekiwaną zmiennej losowej

k

X

Centralne momenty mieszane rzędu r + s zmiennej losowej

)

,

(

l

k

X

X

[

]

s

l

l

r

k

k

rs

kl

EX

X

EX

X

E

)

(

)

(

−

⋅

−

=

µ

Z tej definicji wynika, że:

0

)

(

10

=

−

=

k

k

kl

EX

X

E

µ

dla k, l = 1, 2, ... , n

)

(

)

(

2

20

k

k

k

kl

X

V

EX

X

E

=

−

=

µ

)

(

)

(

0

k

r

r

k

k

r

kl

X

EX

X

E

µ

µ

=

−

=

- r –ty moment centralny zmiennej losowej

k

X

.

Momenty mieszane dla zmiennej losowej dwuwymiarowej ( X, Y )

)

(

s

r

rs

Y

X

E

⋅

=

α

- moment mieszany zwykły,

]

)

(

)

[(

s

r

rs

EY

Y

EX

X

E

−

⋅

−

=

µ

- centralny moment mieszany,

EX

Y

X

E

=

⋅

=

)

(

0

1

10

α

EY

Y

X

E

=

⋅

=

)

(

1

0

01

α

0

)]

[(

10

=

−

=

EX

X

E

µ

bo:

0

)

(

=

−

=

−

∑

∑

∑

i

i

i

i

i

i

i

i

EXp

p

x

p

EX

x

0

)]

[(

01

=

−

=

EY

Y

E

µ

2

2

20

]

)

[(

x

EX

X

E

σ

µ

=

−

=

2

2

02

]

)

[(

y

EY

Y

E

σ

µ

=

−

=

)

,

(

)]

(

)

[(

11

Y

X

Cov

EY

Y

EX

X

E

=

−

⋅

−

=

µ

- moment mieszany 2-go rzędu.

Kowariancja zmiennej losowej dwuwymiarowej ( X, Y )

Definicja:

Kowariancją zmiennej losowej dwuwymiarowej ( X, Y ) nazywamy liczbę

)

,

(

Y

X

Cov

określoną

wzorem:

11

)]

(

)

[(

)

,

(

XY

EY

Y

EX

X

E

Y

X

Cov

µ

=

−

⋅

−

=

Jest to oczywiście centralny moment mieszany rzędu drugiego.
Czyli:

EY

EX

Y

X

E

Y

X

Cov

⋅

−

⋅

=

)

(

)

,

(

gdzie:

∑∑

=

⋅

i

k

ik

k

i

p

y

x

Y

X

E

)

(

- dla zmiennej losowej skokowej ,

oraz:

)

,

(

k

i

ik

y

Y

x

X

P

p

=

=

=

.

∫ ∫

∞

∞

−

∞

∞

−

=

⋅

dxdy

y

x

xyf

Y

X

E

)

,

(

)

(

- dla zmiennej losowej ciągłej.

Twierdzenie 1:
Jeśli zmienne losowe X i Y są niezależne i mają wartości oczekiwane, to:

EY

EX

Y

X

E

⋅

=

⋅

)

(

Twierdzenie 2:

Jeśli:

∞

<

2

EX

i

∞

<

2

EY

, to:

)

,

(

2

)

(

Y

X

Cov

VY

VX

Y

X

V

⋅

±

+

=

±

Twierdzenie 3:

Dla dowolnych liczb

d

c

b

a

,

,

,

zachodzi:

)

,

(

)

,

(

Y

X

Cov

c

a

d

cY

b

aX

Cov

⋅

⋅

=

+

+

Twierdzenie 4:

Y

X

Y

X

Cov

σ

σ ⋅

≤

)

,

(

Współczynnik korelacji

XY

ρ

zmiennych losowych X, Y

Niech zmienne losowe X i Y posiadają momenty dwóch pierwszych rzędów:

EX

m

X

=

,

EY

m

Y

=

,

0

)

(

2

>

=

X

V

X

σ

,

0

)

(

2

>

=

Y

V

Y

σ

.

Współczynnik korelacji jest parametrem służącym do badania zależności między zmiennymi losowymi X i
Y . Służy on do dwóch celów:

a) zaprzeczeniu zdania: zmienne losowe X i Y są niezależne,
b) pokazaniu, że między zmiennymi losowymi X i Y istnieje zależność liniowa z

prawdopodobieństwem 1.

Definicja:

Współczynnikiem korelacji

XY

ρ

zmiennych losowych X i Y nazywamy liczbę:

Y

X

Y

X

Y

X

XY

Y

X

Cov

m

Y

m

X

E

σ

σ

σ

σ

ρ

)

,

(

)}

)(

{(

=

−

−

=

Własności współczynnika korelacji

Twierdzenie 5:
Wartość bezwzględna współczynnika korelacji jest niezmiennikiem przekształceń liniowych, czyli:

|

|

|

|

,

,

,

0

,

d

cY

b

aX

XY

d

b

c

a

+

+

≠

=

∧

ρ

ρ

, czyli:

|

)

,

(

|

|

)

,

(

|

Y

X

d

cY

b

aX

ρ

ρ

=

+

+

Twierdzenie 6:
Moduł współczynnika korelacji jest nie większy od jedności:

1

|

|

≤

XY

ρ

Twierdzenie 7:

Jeśli zmienne losowe X i Y są niezależne, to

0

=

XY

ρ

.

O zmiennych losowych, dla których

0

=

XY

ρ

mówimy, że są nieskorelowane.

Praktyczne znaczenie współczynnika korelacji

Rozważmy zależność liniową zmiennych losowych X i Y :

b

aX

Y

+

=

Obliczmy współczynnik korelacji zmiennych losowych X i Y :

Y

X

XY

Y

X

Cov

σ

σ

ρ

)

,

(

=

=

−

−

−

+

=

−

−

=

)]

)(

[(

)]

)(

[(

)

,

(

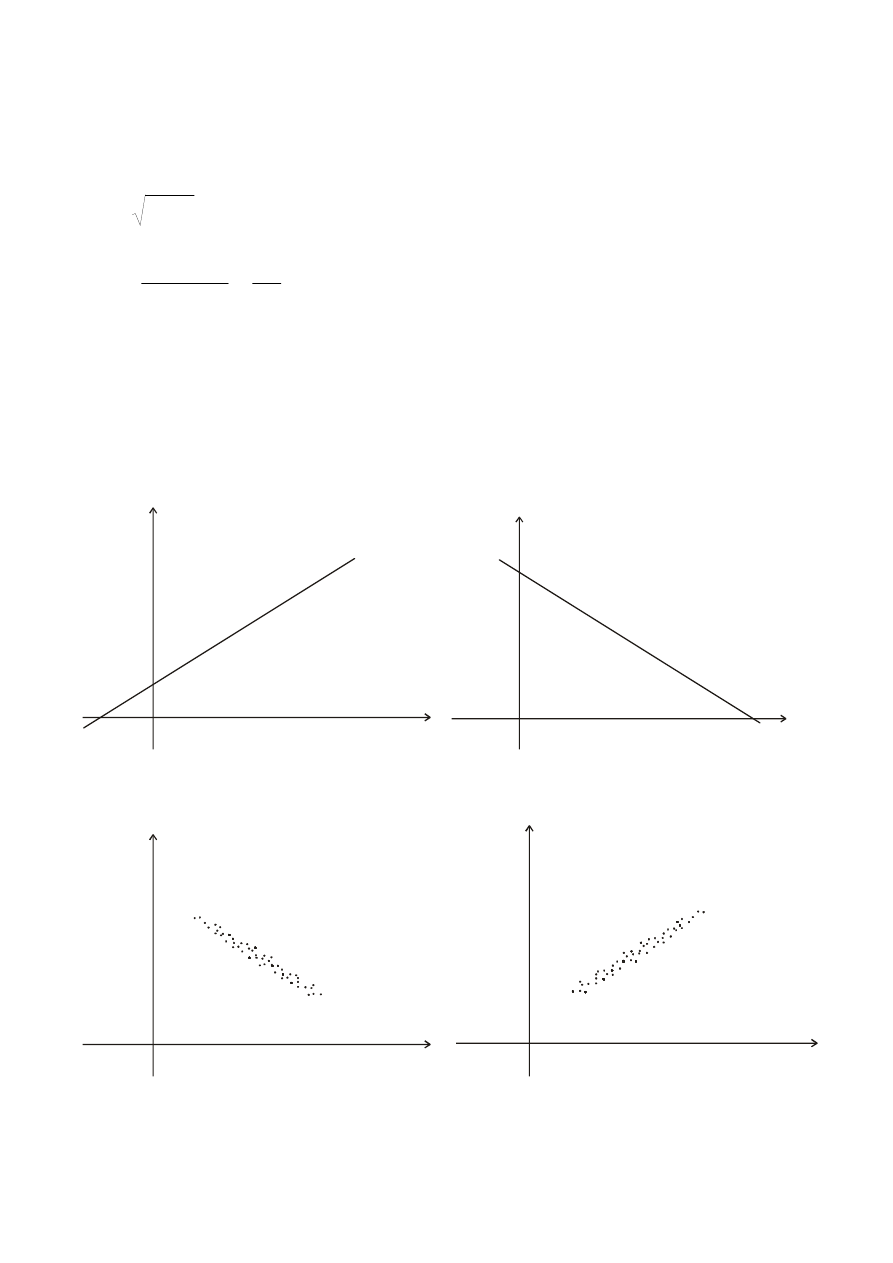
EX

X

b

aEX

b

aX

E

EX

X

EY

Y

E

Y

X

Cov

=

−

=

−

=

−

−

=

]

)

[(

]

)

(

[

)]

)(

(

[

2

2

EX

X

aE

EX

X

a

E

EX

X

EX

X

a

E

2

X

a

σ

=

2

2

2

2

2

2

]

))

(

[(

]

)

[(

]

)

[(

X

Y

a

EX

X

a

E

b

aEX

b

aX

E

EY

Y

E

σ

σ

=

−

=

−

−

+

=

−

=

X

X

Y

a

a

σ

σ

σ

|

|

2

2

=

=

Zatem współczynnik korelacji wyniesie:

|

|

|

|

2

a

a

a

a

X

X

X

XY

=

=

σ

σ

σ

ρ

Czyli współczynnik korelacji tych zmiennych losowych wyraża się wzorem:









<

−

>

=

0

1

0

1

a

dla

a

dla

XY

ρ

Dla

1

=

XY

ρ

i

1

−

=

XY

ρ

zależność stochastyczna przechodzi w zależność funkcyjną:

y

a>0

x

Y=

aX

+b

y

a<0

x

Y=a

X+b

1

=

XY

ρ

1

−

=

XY

ρ

y

x

y

x

0

1

<

<

−

XY

ρ

1

0

<

<

XY

ρ

y

x

0

=

XY

ρ

- zmienne losowe nieskorelowane.

Rozkłady brzegowe zmiennych losowych dwuwymiarowych (

X, Y )

Dla dwuwymiarowej zmiennej losowej ( X, Y ) funkcje dystrybuant:

)

,

(

)

(

lim

y

x

F

x

F

y

X

∞

→

=

)

,

(

)

(

lim

y

x

F

y

F

x

Y

∞

→

=

są funkcjami jednej zmiennej losowej, odpowiednio x oraz y i każda z nich ma wszystkie własności
dystrybuanty jednowymiarowej.

Definicja:

Funkcje

X

F

oraz

Y

F

, otrzymane jako odpowiednie wartości graniczne funkcji

F

, nazywamy

dystrybuantami brzegowymi, a jednowymiarowe rozkłady prawdopodobieństwa wyznaczone przez funkcje

X

F

oraz

Y

F

, nazywamy rozkładami brzegowymi.

W przypadku zmiennej losowej dwuwymiarowej ( X, Y ) typu ciągłego o funkcji gęstości

prawdopodobieństwa

)

,

(

y

x

f

, mamy:

∫

ℜ

=

1

)

,

(

)

(

dy

y

x

f

x

f

X

,

∫

ℜ

=

1

)

,

(

)

(

dx

y

x

f

y

f

Y

Funkcje

)

(x

f

X

i

)

( y

f

Y

są funkcjami gęstości prawdopodobieństwa odpowiednio zmiennych losowych

X oraz Y i nazywać je będziemy brzegowymi gęstościami prawdopodobieństwa.

Oczywiście zachodzi:

)

(

)

(

x

f

x

F

x

X

X

=

∂

∂

,

)

(

)

(

y

f

y

F

y

Y

Y

=

∂

∂

Dla zmiennej losowej dwuwymiarowej typu skokowego o rozkładzie określonym parami liczb

)

,

(

k

i

y

x

p

,

mamy:

∑

=

k

k

i

i

X

y

x

p

x

p

)

,

(

)

(

,

∑

=

i

k

i

k

Y

y

x

p

y

p

)

,

(

)

(

Liczby

)

(

i

X

x

p

- wyznaczają rozkład brzegowy prawdopodobieństwa zmiennej losowej X.

Liczby

)

(

k

Y

y

p

- wyznaczają rozkład brzegowy prawdopodobieństwa zmiennej losowej Y.

Zostały one określone jako odpowiednie sumy prawdopodobieństw

)

,

(

k

i

y

x

p

dwuwymiarowej zmiennej

losowej ( X, Y ).
Znając rozkład dwuwymiarowej zmiennej losowej ( X, Y ), możemy zawsze wyznaczyć dla niej 2 rozkłady
brzegowe:

- brzegowy rozkład prawdopodobieństwa zmiennej losowej X,
- brzegowy rozkład prawdopodobieństwa zmiennej losowej Y.

Rozumowanie odwrotne nie jest prawdziwe, tzn. znając rozkłady brzegowe, na ogół, nie można
jednoznacznie wyznaczyć rozkładu prawdopodobieństwa dwuwymiarowego.

Zmienne losowe niezależne

Definicja:
Dana jest zmienna losowa dwuwymiarowa ( X, Y ). Zmienne losowe X i Y nazywamy niezależnymi
jeśli zachodzą relacje:

- dla zmiennych losowych typu skokowego:

)

(

)

(

)

,

(

,

y

F

x

F

y

x

F

Y

X

y

x

⋅

=

∧

lub

)}

(

)

(

)

,

(

{

,

k

Y

i

X

k

i

y

x

y

p

x

p

y

x

p

k

i

⋅

=

∧

- dla zmiennych losowych typu ciągłego:

)

(

)

(

)

,

(

,

y

f

x

f

y

x

f

Y

X

y

x

⋅

=

∧

Przykład 2:
Rozpatrzmy dwuwymiarową zmienną losową ( X, Y ) typu skokowego przyjmującą skończoną

liczbę wartości

)

,

(

k

i

y

x

i = 1, 2, ..., r k = 1, 2, ..., m z prawdopodobieństwami

)

,

(

)

,

(

k

i

k

i

y

Y

x

X

P

y

x

p

=

=

=

.

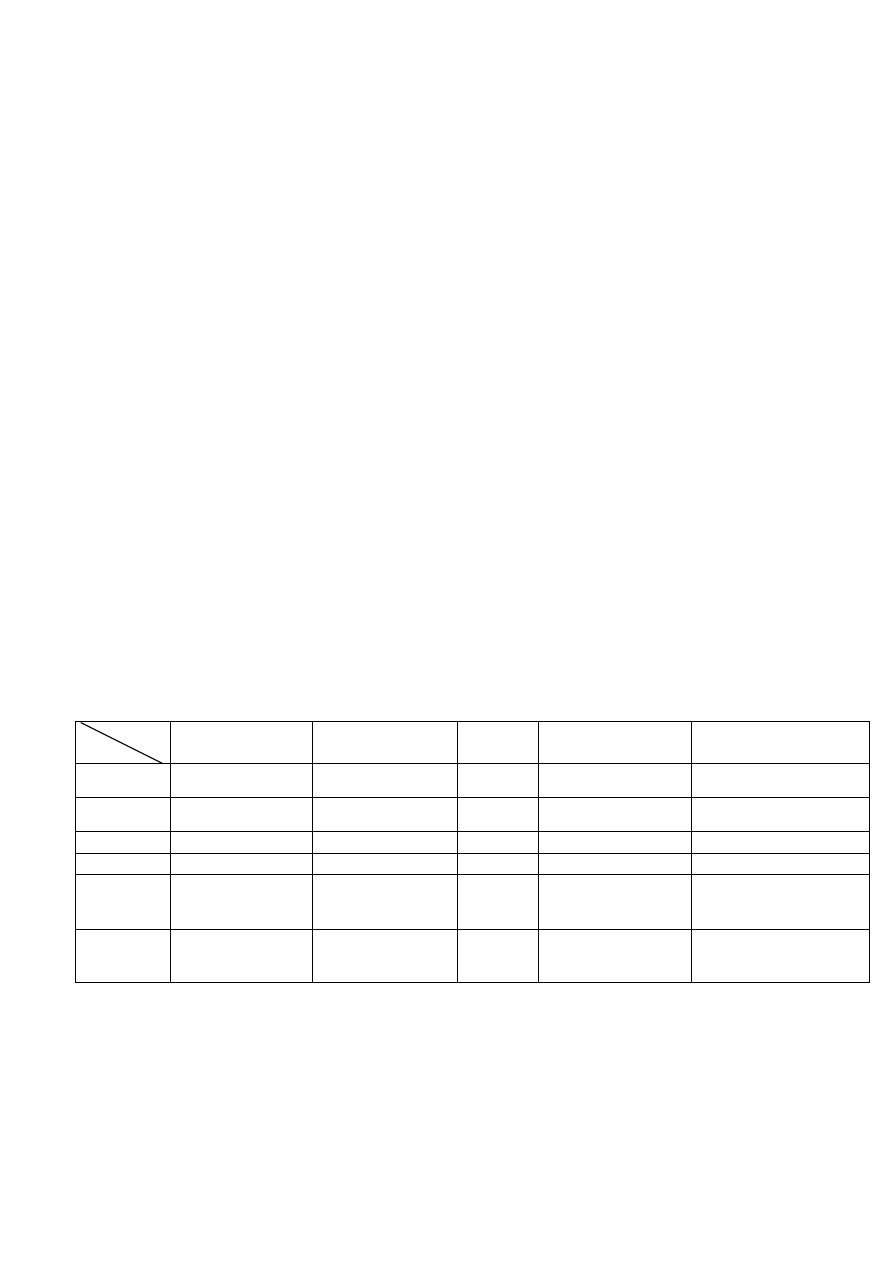
Przedstawmy naszą dwuwymiarową zmienną losową ( X, Y ) za pomocą tabeli:

Y
X

1

y

2

y

...

m

y

Rozkłady brzegowe zm. l.
X

1

x

11

1

1

)

,

(

p

y

x

p

=

12

2

1

)

,

(

p

y

x

p

=

...

m

m

p

y

x

p

1

1

)

,

(

=

.

1

p

2

x

21

1

2

)

,

(

p

y

x

p

=

22

2

2

)

,

(

p

y

x

p

=

m

m

p

y

x

p

2

2

)

,

(

=

.

2

p

.

.

.

...

.

.

.

.

.

...

.

.

r

x

1

1

)

,

(

r

r

p

y

x

p

=

2

2

)

,

(

r

r

p

y

x

p

=

...

rm

m

r

p

y

x

p

=

)

,

(

.

r

p

Rozkłady
brzegowe zm.
l. Y

1

.

p

2

.

p

...

m

p

.

1

.

.

=

=

∑

∑

i

i

k

k

p

p

gdzie:

m

p

p

p

p

1

12

11

.

1

...

+

+

+

=

m

p

p

p

p

2

22

21

.

2

...

+

+

+

=

rm

r

r

r

p

p

p

p

+

+

+

=

...

2

1

.

- rozkłady brzegowe zmiennej losowej X,

1

21

11

1

.

...

r

p

p

p

p

+

+

+

=

2

22

12

2

.

...

r

p

p

p

p

+

+

+

=

rm

m

m

m

p

p

p

p

+

+

+

=

...

2

1

.

- rozkłady brzegowe zmiennej losowej Y.

Oczywiście, zachodzi:

∑

∑

=

=

=

m

k

k

i

r

i

y

x

p

1

1

1

)

,

(

Zmienne losowe typu skokowego X i Y są niezależne, jeśli zachodzi:

k

i

ik

k

i

p

p

p

.

.

,

⋅

=

∧

Znając rozkłady brzegowe zmiennych losowych X i Y , możemy z nich łatwo wyznaczyć wartości
oczekiwane i wariancje tych zmiennych losowych:

∑

=

r

i

i

i

p

x

EX

.

,

∑

=

m

k

k

k

p

y

EY

.

2

.

2

)

(

)

(

EX

p

x

X

E

r

i

i

i

−

=

∑

,

2

.

2

)

(

)

(

EY

p

y

Y

V

m

k

k

k

−

=

∑

Dla dwuwymiarowej zmiennej losowej z przykładu 1, rozkłady brzegowe będą następujące:

Y
X

0

1

rozkł. brzeg. zm. l. Y

1

1/12

1/12

.

1

p

= 1/6

2

1/12

1/12

.

2

p

= 1/6

3

1/12

1/12

.

3

p

= 1/6

4

1/12

1/12

.

4

p

= 1/6

5

1/12

1/12

.

5

p

= 1/6

6

1/12

1/12

.

6

p

= 1/6

rozkł. brzeg. zm. l. X

1

.

p

= 1/2

2

.

p

=1/2

1

Zadania

1. Dwuwymiarowa zmienna losowa (X, Y) ma rozkład prawdopodobieństwa:

Y
X

0

1

1

1/6

1/6

2

2/6

2/6

Zbadać, czy zmienne losowe X oraz Y są niezależne.

2. Dwuwymiarowa zmienna losowa (X, Y) ma rozkład prawdopodobieństwa:

Y
X

1

2

3

0

0,3

0,2

0,1

1

0,2

0,1

0,1

a) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej :

Y

X

Z

+

=

2

.

b) Sprawdzić, czy zmienne losowe X i Y są niezależne?

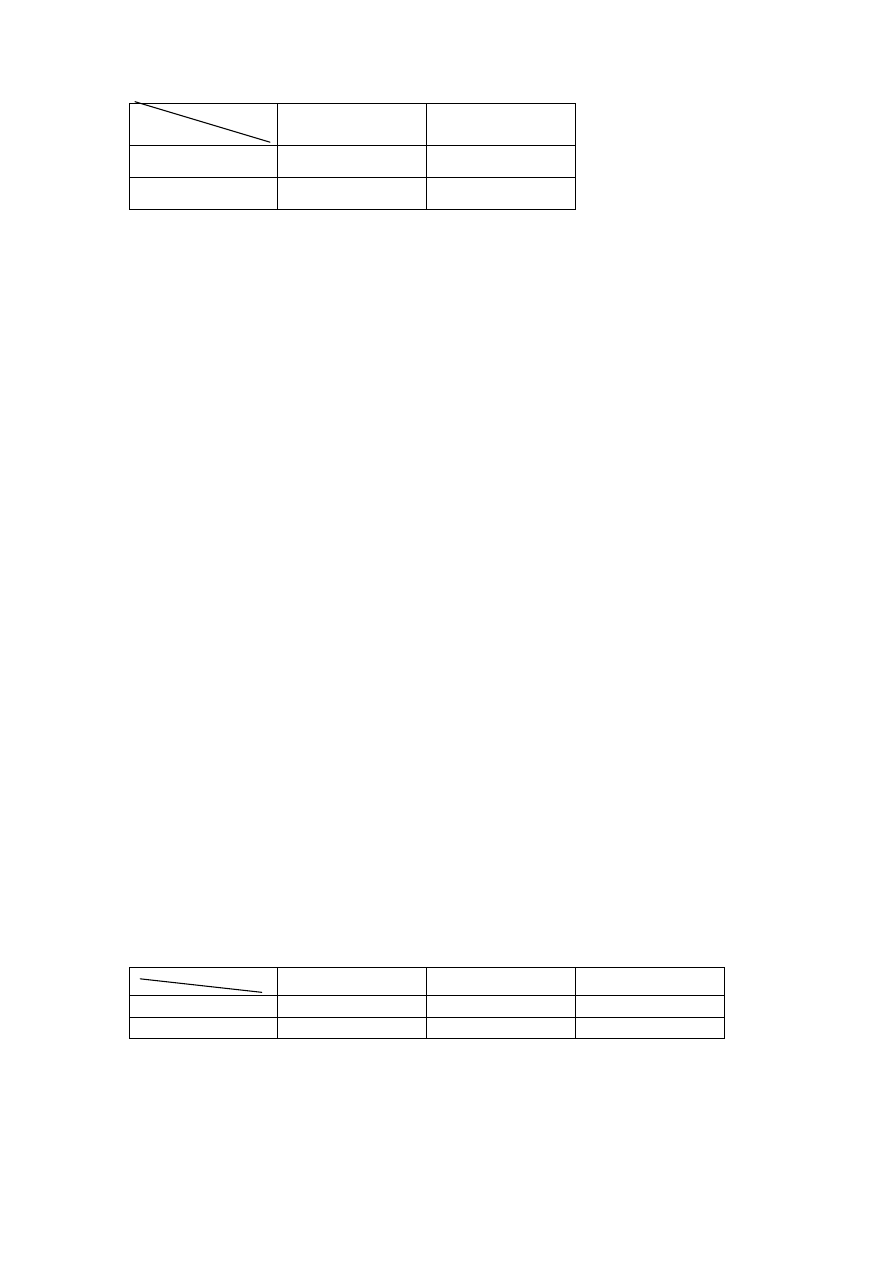
3. Dwuwymiarowa zmienna losowa (X, Y) ma rozkład prawdopodobieństwa:

Y
X

0

1

1

1/8

12

p

2

21

p

1/4

gdzie:

21

p

= prawdopodobieństwu wypadnięcia liczby parzystej przy rzucie kostką.

Obliczyć współczynnik korelacji

XY

ρ

zmiennych losowych X i Y.

4. Wyznaczyć stałą c tak, aby funkcja:









<

<

=

obszarem

tym

poza

y

x

dla

c

y

x

f

0

1

|

|

,

1

|

|

)

,

(

a) była funkcją gęstości prawdopodobieństwa zmiennej losowej (X, Y) typu ciągłego,

b) obliczyć prawdopodobieństwo:

)

0

,

0

(

>

>

Y

X

P

.

5. Zmienna losowa X ma rozkład normalny N( 2 ; 1 ), zaś zmienna losowa Y ma rozkład normalny

N( 1 ; 2 ). Zmienne losowe X i Y są zależne, a współczynnik korelacji między nimi wynosi 0,4.

Obliczyć wartość oczekiwaną i wariancję zmiennej losowej

10

3

2

−

−

=

Y

X

Z

.

6. Zmienna losowa X ma rozkład normalny o wartości oczekiwanej 10 i wariancji 4.

a) Obliczyć kwantyl rzędu ¼ w tym rozkładzie.

b) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej

20

3

+

−

=

X

Y

.

7. Sprzedawca zatrudniony w sklepie komputerowym dostaje miesięczną stałą pensję w wysokości

500,- zł, a do tego 10,- zł za każdy sprzedany komputer i 20,- zł za każdy sprzedany zestaw
oprogramowania. W ciągu miesiąca udaje mu się sprzedać średnio 40 komputerów oraz 20
zestawów oprogramowania z odchyleniem standardowym odpowiednio 10 i 5. Współczynnik
korelacji pomiędzy liczbą sprzedanych komputerów i liczbą sprzedanych zestawów
oprogramowania wynosi 0,5.

Obliczyć średnie miesięczne wynagrodzenie tego sprzedawcy oraz odchylenie standardowe
miesięcznego wynagrodzenia.

8. Pewna firma budowlana prowadzi działalność w Warszawie oraz poza Warszawą. Badania

dotyczące działalności firmy w ciągu ostatnich lat pokazały, że rozkład prawdopodobieństwa liczby
inwestycji prowadzonych jednocześnie w Warszawie oraz poza Warszawą można przedstawić
tabelarycznie:

Poza Warszawą

W Warszawie

0

1

2

0

0,1

0,3

0,2

1

0,2

0,1

0,1

a) Czy liczby inwestycji prowadzonych jednocześnie w Warszawie i poza są niezależne?
b) Czy liczby inwestycji w Warszawie i poza są skorelowane i w jakim stopniu?
c) Jaka jest wartość oczekiwana i wariancja łącznej liczby inwestycji prowadzonych

jednocześnie w Warszawie i poza Warszawą?