Zmienne losowe

skokowe

dr Tomasz Kowalski

Wykład 23

Slajd 2 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

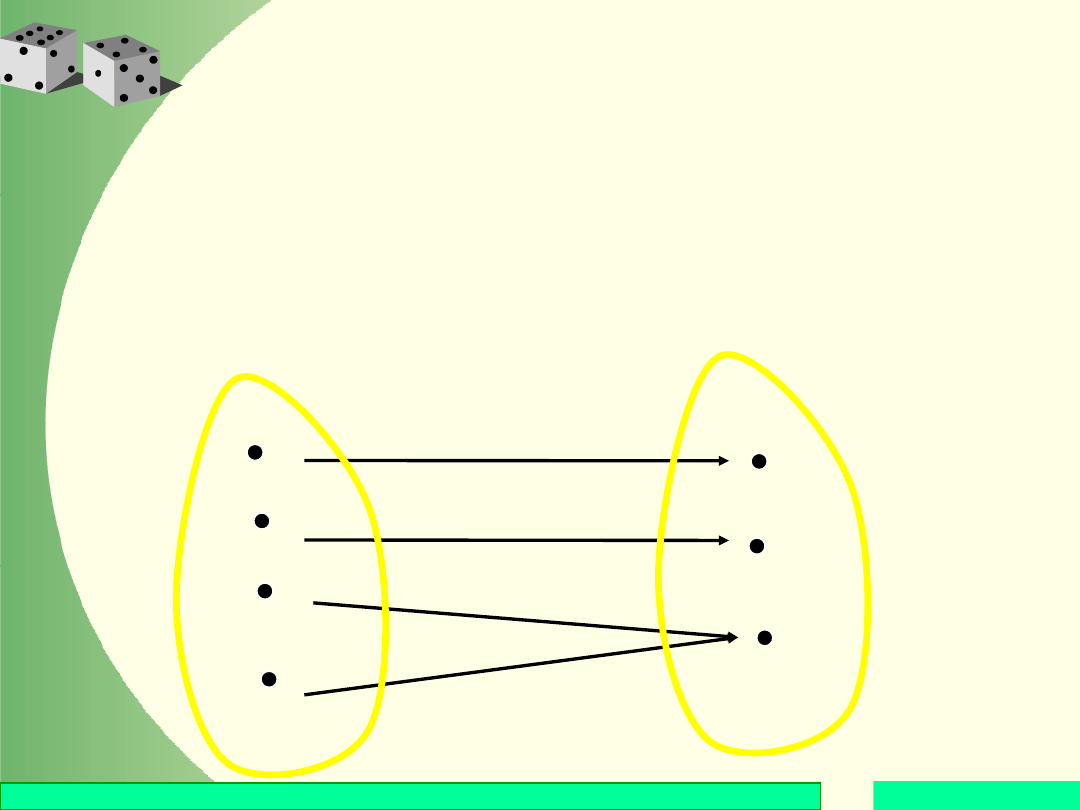
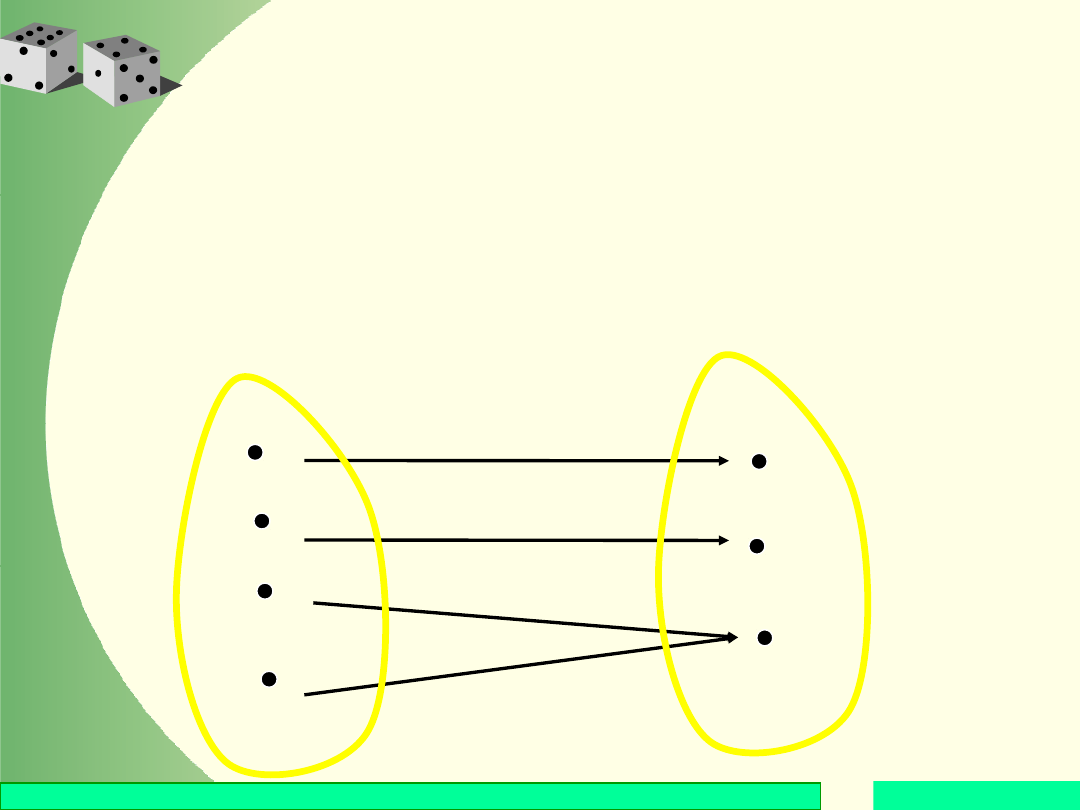
Definicja zmiennej losowej

Zmienną losową X nazywa się funkcję, która
zdarzeniom elementarnym  pewnej przestrzeni

probabilistycznej  przyporządkowuje liczby

rzeczywiste.

Zapisujemy wtedy:

X:   R.









X(

X(





)

)

Slajd 3 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rzucamy dwiema kostkami do gry. Jeżeli każdemu
wynikowi (zdarzeniu) przyporządkujemy sumę
uzyskanych oczek, to mamy do czynienia ze
zmienną losową X:   R.

 





{( ,

) ;

, ,..., ,

, ,..., }

x y

x

y

i

j

i

j

1 2

6

1 2

6

( , )

.

i

j

i

j

X x y

x

y

= +

Zmienna ta przyjmuje wartości naturalne od 2 do 12.

Slajd 4 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Dokonujemy losowego wyboru punktu z odcinka
[0; 1]. Każdej wylosowanej liczbie
przyporządkowujemy jej kwadrat. Wówczas mamy
do czynienia ze zmienną losową

X:   R.

[0;1]

W=

2

( )

.

X x

x

=

Zmienna ta przyjmuje każdą wartość z
przedziału [0; 1]

Slajd 5 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rodzaje zmiennych

losowych

Zmienną losową nazywamy dyskretną lub
skokową, jeżeli zbiór jej wartości jest skończony
lub daje się ustawić w ciąg.

Jeżeli zmienna losowa przyjmuje każdą wartość z
pewnego przedziału, to nazywamy ją zmienną
losową ciągłą.

Każda zmienna określona na przestrzeni
probabilistycznej o skończonej liczbie elementów
jest więc dyskretna.

Slajd 6 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład zmiennej losowej

dyskretnej

Rozkładem zmiennej losowej dyskretnej nazywa się
zbiór par utworzonych z wartości tej zmiennej i
prawdopodobieństw, z jakimi są one przyjmowane.

Slajd 7 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

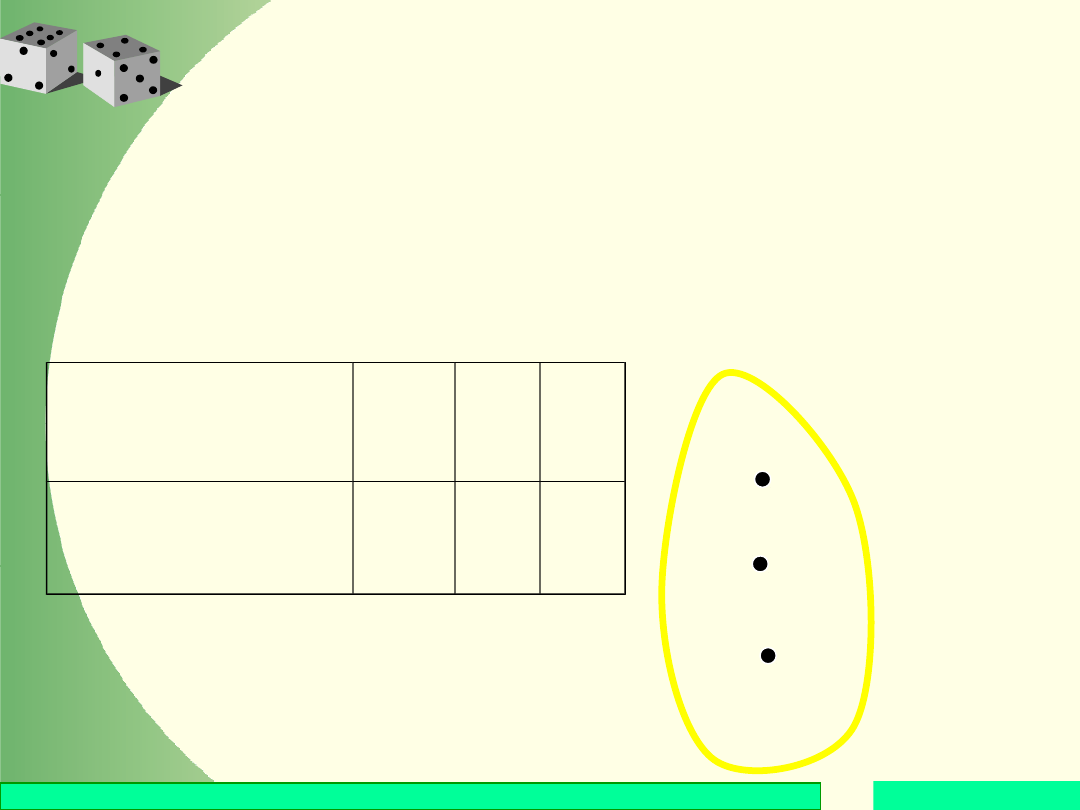
Przykład

Rozpatrzmy zmienną losową X, która rzutowi dwiema
monetami przypisuje liczbę uzyskanych orłów:

0

1

2

RR

RO

OR

OO

¼

¼

¼

¼



Slajd 8 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

0

1

2

¼

½

¼

RR

RO

OR

OO

¼

¼

¼

¼



Rozkład zmiennej

losowej X

Rozpatrzmy zmienną losową X, która rzutowi dwiema
monetami przypisuje liczbę uzyskanych orłów:

Slajd 9 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład tej zmiennej losowej można
przedstawić w postaci tabelki:

0

1

2

¼

½

¼

Rozkład zmiennej

losowej X

Wartości

przyjmowane

przez X

Prawdopodobieńst

wo

¼

¼

½

0

1

2

Slajd 10 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rzucamy trzema monetami. Niech X będzie
zmienną losową, która otrzymanemu wynikowi
doświadczenia przypisuje liczbę uzyskanych orłów.
Zmienna przyjmuje więc wartości: 0, 1, 2, 3, przy
czym wartość k osiągana jest z
prawdopodobieństwem, które można obliczyć
stosując wzór Bernoulli’ego:

3

.

3

1

1

(

)

2

2

k

k

P X k

k

-

� �� � � �

= =

�

�

� �� � � �

� � � �

� �

Slajd 11 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

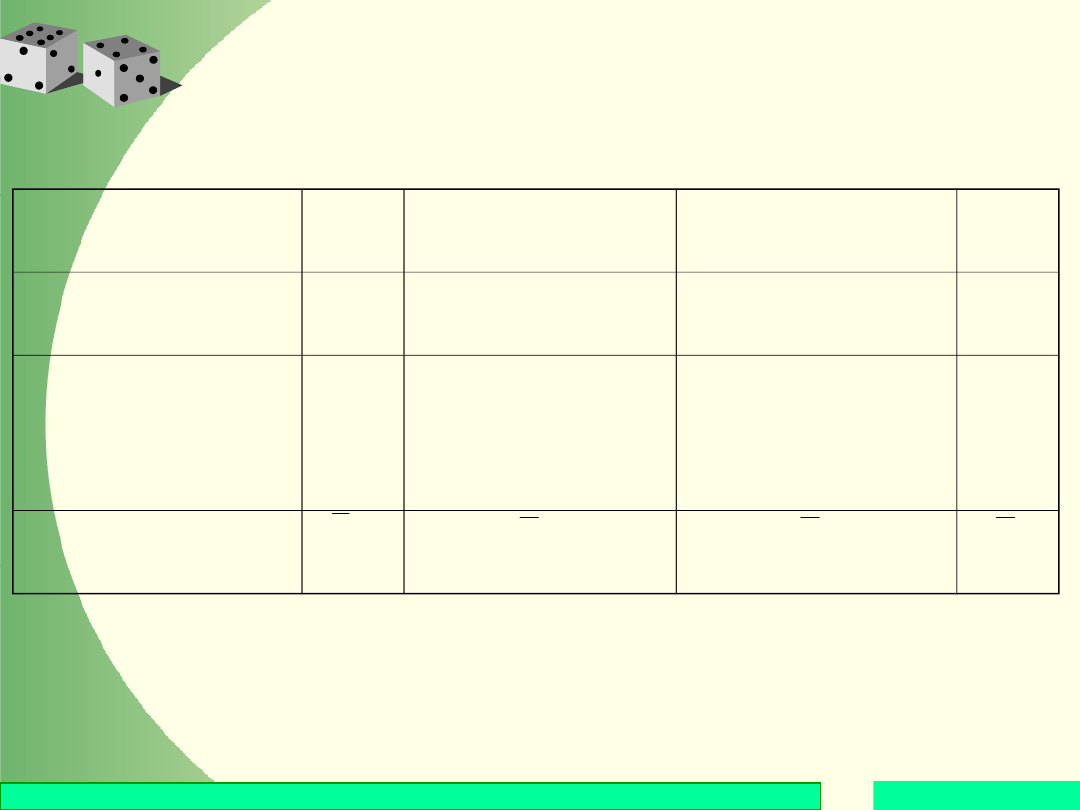
Przykład

Zdarzenia

(r,r,r)

(o,r,r), (r,o,r),

(r,r,o)

(o,o,r),(o,r,o),

(r,o,o)

(o,o,

o)

Wartości przyj-

mowane przez X

0

1

2

3

Liczba zdarzeń,

którym

przypisano te

wartości

1

3

3

1

Prawdopodobień

stwo

1
8

1
8

3

8

3

8

Slajd 12 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

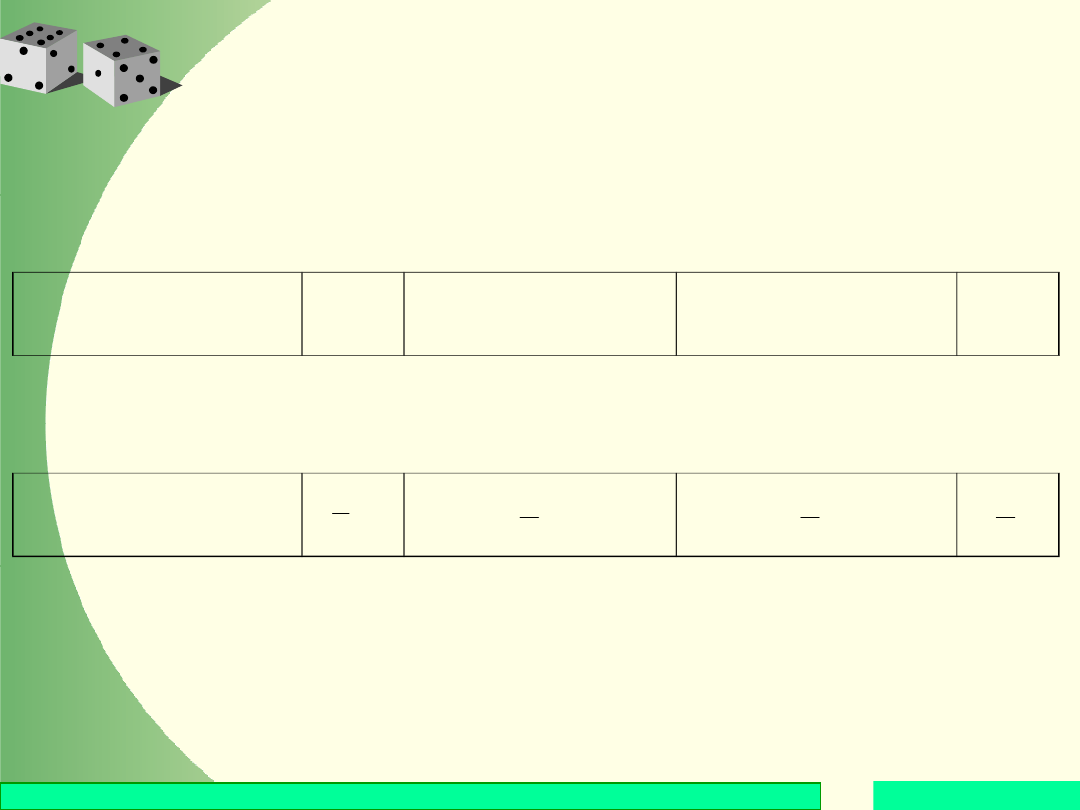
Przykład

Wartości przyj-

mowane przez X

0

1

2

3

Prawdopodobień

stwo

1
8

1
8

3

8

3

8

Slajd 13 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

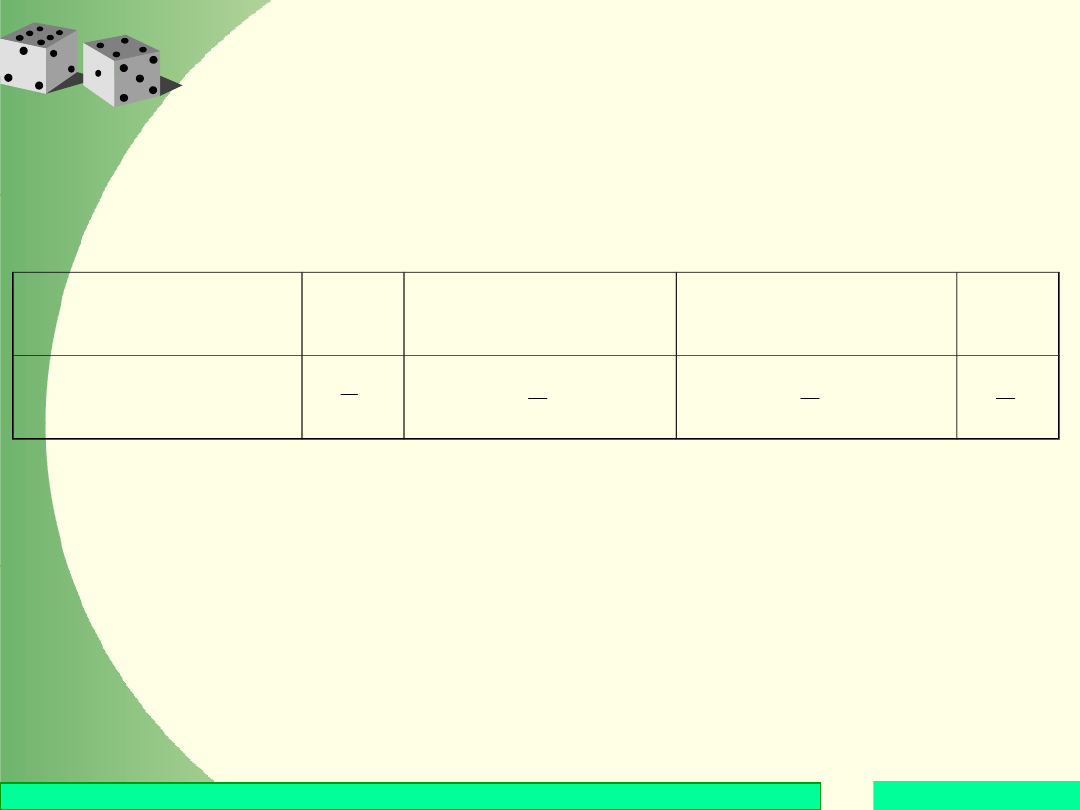
Przykład

Wartości przyj-

mowane przez X

0

1

2

3

Prawdopodobień

stwo

1
8

1
8

3

8

3

8

Slajd 14 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

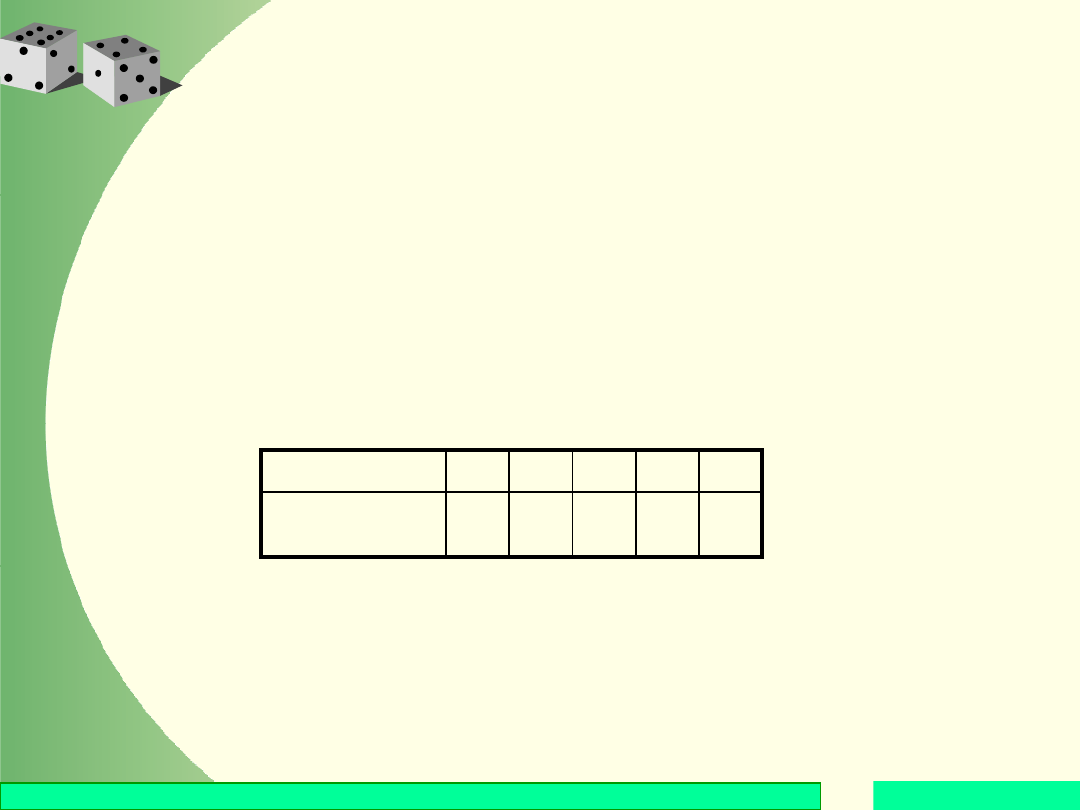
Rozkład zmiennej losowej

Funkcję przypisującą wszystkim wartościom zmiennej
skokowej X prawdopodobieństwa, z jakimi są te
wartości przyjmowane, nazywamy funkcją rozkładu
prawdopodobieństwa tej zmiennej.

Rozkład prawdopodobieństwa zmiennej losowej
skokowej przedstawiany jest najczęściej w postaci
dwuwierszowej tabelki:

k

x

1

x

2

x

…

n

x

…

k

p

1

p

2

p

…

n

p

…

Liczby x

1

, x

2

, …,x

n

nazywamy punktami skokowymi

zmiennej X, a prawdopodobieństwa p

1

, p

2

, …,p

n

–

skokami.

1.

k

k

p =

�

Prawdopodobieństwa te są liczbami
dodatnimi i spełniają tzw. warunek
unormowania:

Slajd 15 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Histogram rozkładu

Wykresem funkcji prawdopodobieństwa w
prostokątnym układzie współrzędnych jest zbiór
punktów: (x

1

, p

1

), (x

2

, p

2

),…, (x

n

, p

n

).

Jeżeli każdy z tych punktów połączyć odcinkiem z
punktem odpowiednio: (x

1

, 0), (x

2

, 0),…, (x

n

, 0). , to

otrzymamy tzw. histogram funkcji
prawdopodobieństwa.

Slajd 16 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

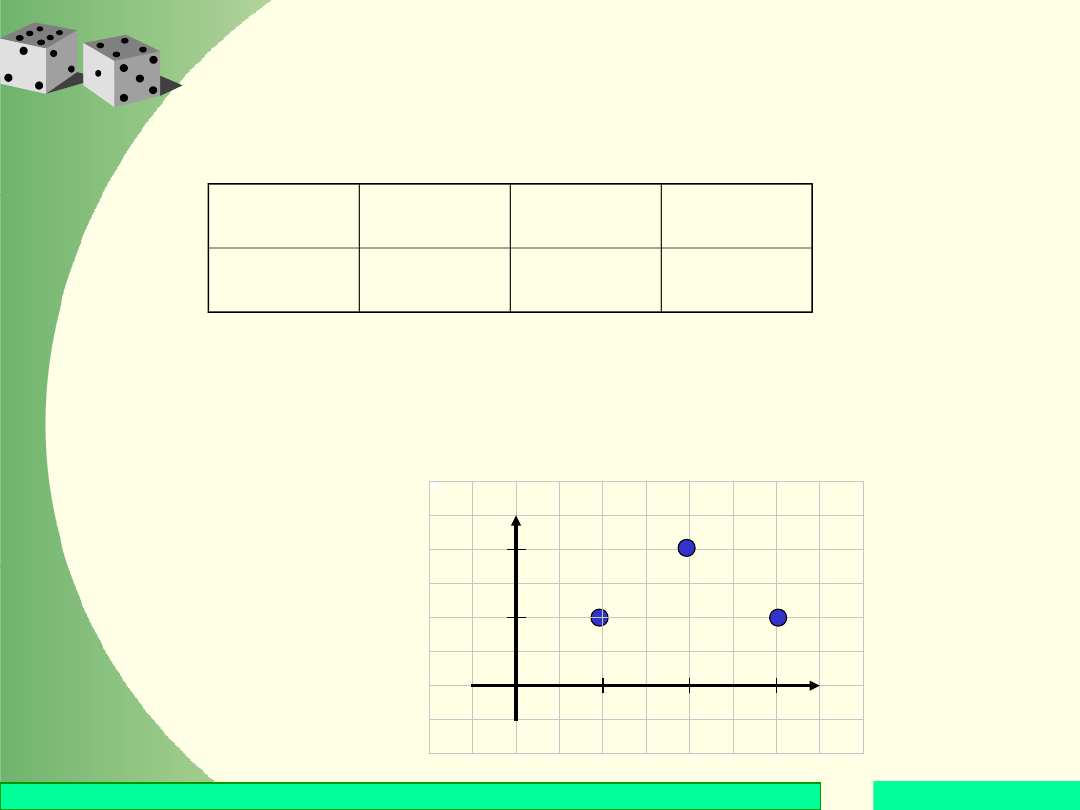
Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

¼

½

¼

Sprawdzić, czy prawdopodobieństwa spełniają warunek
unormowania. Sporządzić wykres funkcji
prawdopodobieństwa oraz histogram tego rozkładu.

1 1 1

1

4 2 4

k

k

p = + + =

�

Warunek unormowania:

jest
spełniony.

Slajd 17 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

¼

½

¼

Sprawdzić, czy prawdopodobieństwa spełniają warunek
unormowania. Sporządzić wykres funkcji
prawdopodobieństwa oraz histogram tego rozkładu.

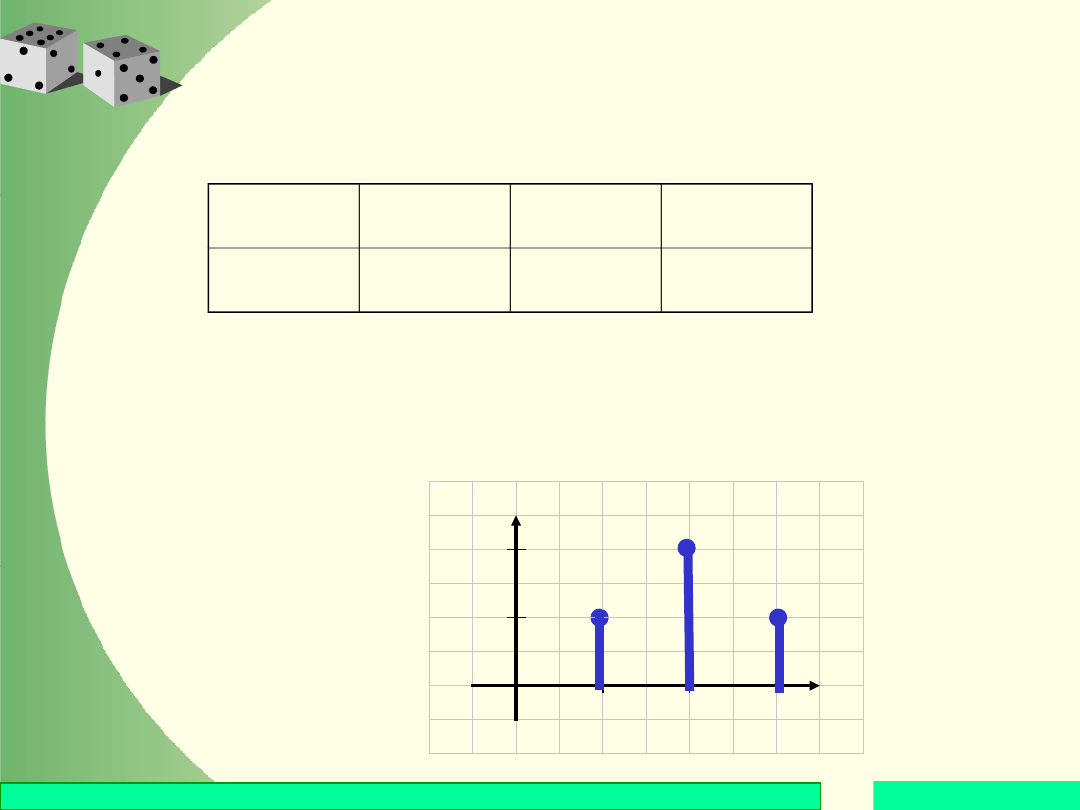
Wykres funkcji
prawdopodobieńst
wa:

1

2

3

X

¼

½

p

Slajd 18 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

¼

½

¼

Sprawdzić, czy prawdopodobieństwa spełniają warunek
unormowania. Sporządzić wykres funkcji
prawdopodobieństwa oraz histogram tego rozkładu.

Histogram
rozkładu:

1

2

3

X

¼

½

p

Slajd 19 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Dystrybuanta zmiennej losowej

Każdej zmiennej losowej X można przypisać
funkcję określoną w zbiorze liczb rzeczywistych
wzorem:

F(x) = p(X < x),

którą nazywamy dystrybuantą zmiennej losowej X.

Wartość dystrybuanty zmiennej losowej w punkcie x
jest prawdopodobieństwem wszystkich tych zdarzeń
elementarnych, którym zmienna losowa przypisała
wartość mniejszą niż x.

Slajd 20 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Własności dystrybuanty

1. Dla każdego xR mamy 0  F(x)  1.

2. lim ( )

(

) 0, lim ( )

(

) 1.

x

x

F x

F

F x

F

�- �

�+�

= - � =

= +� =

3. F jest funkcją niemalejącą.

4. F jest funkcją (co najmniej) lewostronnie

ciągłą w każdym punkcie.

Slajd 21 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Dystrybuanta zmiennej losowej

skokowej

Dystrybuantą zmiennej losowej skokowej X jest
funkcja F określona wzorem

gdzie sumowanie odbywa się po tych k, dla
których x

k

spełniają nierówność x

k

< x.

(

)

:

( )

,

k

k x

x

k

F x

P X x

p

<

=

< =

�

Slajd 22 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

½

¼

¼

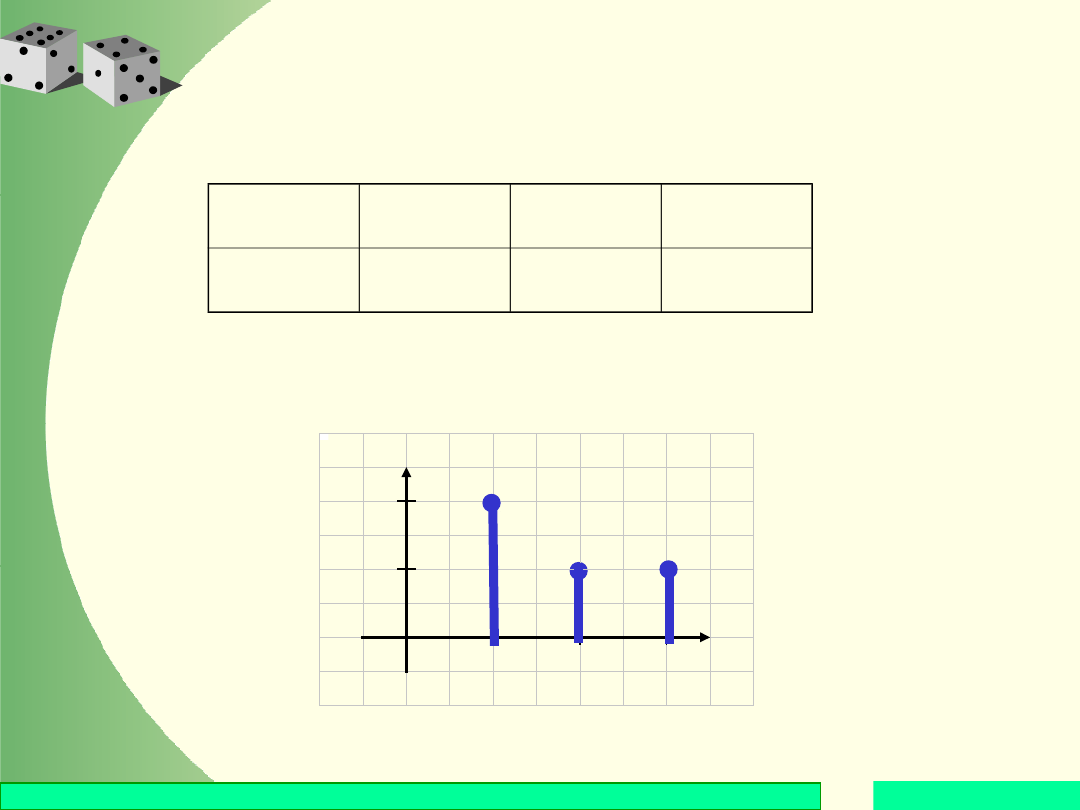
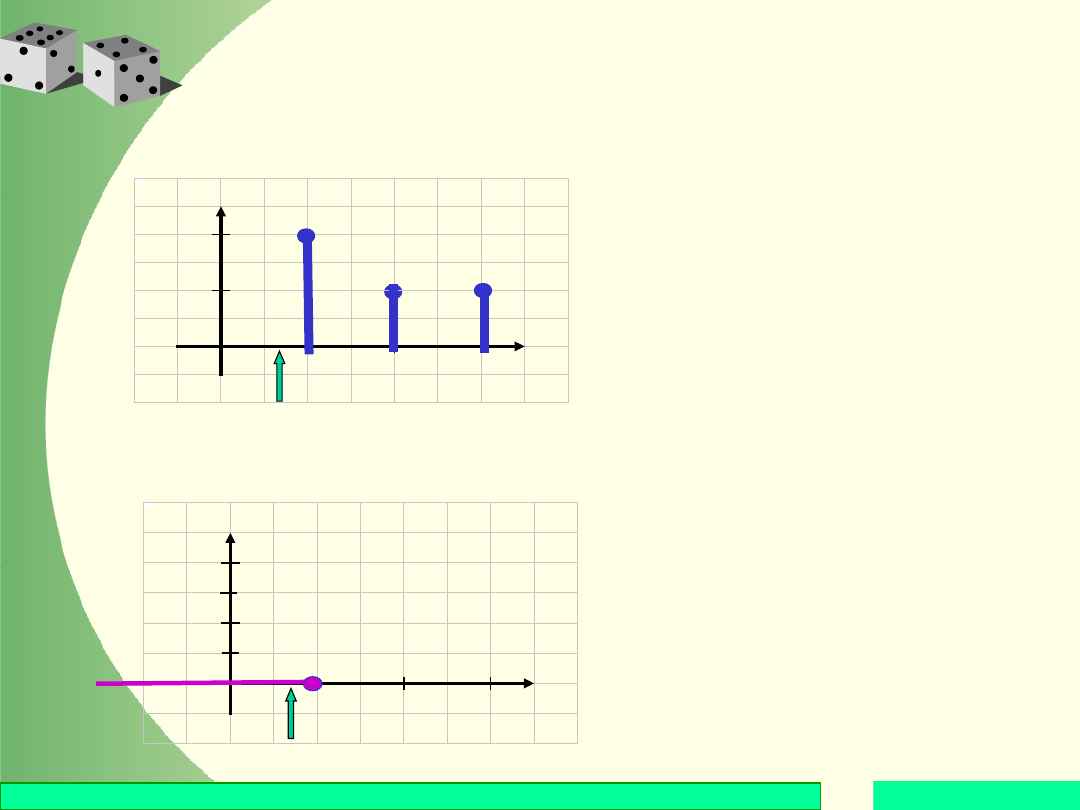
Sporządzić histogram tego rozkładu oraz wykres
dustrybuanty.

Histogram
rozkładu:

1

2

3

X

¼

½

p

Slajd 23 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Histogram
rozkładu:

1

2

3

X

¼

½

p

Dystrybuanta
rozkładu:

1

2

3

X

½

p

1

Gdy x  1, to w

przedziale (–; x) nie

ma punktów
skokowych, zatem F(x)
= 0.

1 4 4 4 4 4 2 4 4 4 4 4 3

Slajd 24 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Histogram
rozkładu:

1

2

3

X

¼

½

p

Dystrybuanta
rozkładu:

1

2

3

X

½

p

1

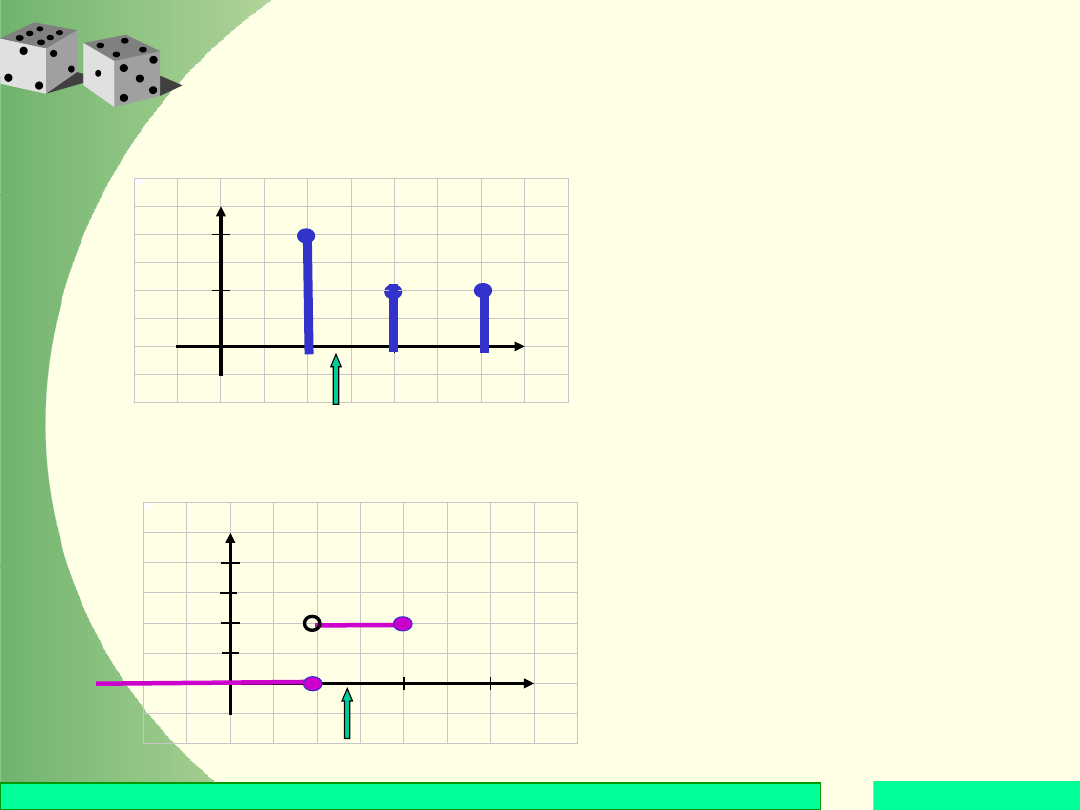
Gdy 1 < x  2, to w

przedziale (–; x) jest

jeden punkt skokowy,
któremu odpowiada
prawdopodobieństwo
½ zatem F(x) = ½.

1 4 4 4 4 4 2 4 4 4 4 4 3

Slajd 25 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Histogram
rozkładu:

1

2

3

X

¼

½

p

Dystrybuanta
rozkładu:

1

2

3

X

½

p

1

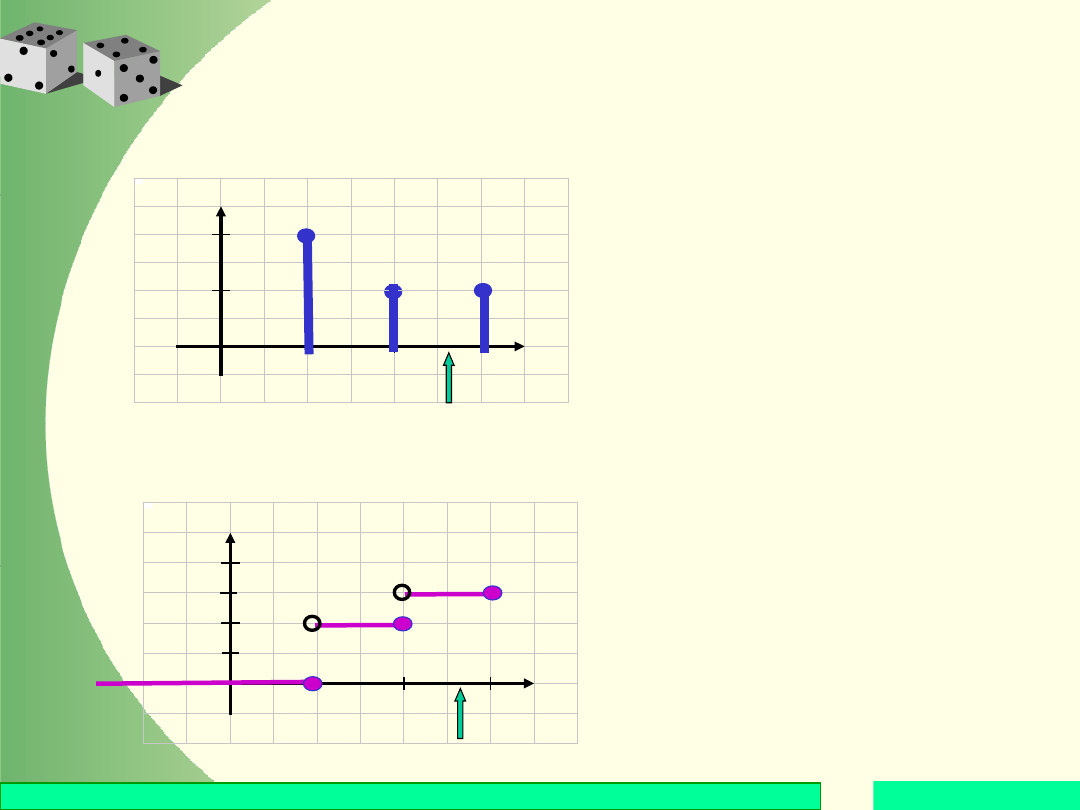
Gdy 2 < x  3, to w

przedziale (–; x) są

dwa punkty skokowe,
którym odpowiada
łączne
prawdopodobieństwo
3/4 zatem F(x) = 3/4.

1 4 4 4 4 4 2 4 4 4 4 4 3

Slajd 26 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Histogram
rozkładu:

1

2

3

X

¼

½

p

Dystrybuanta
rozkładu:

1

2

3

X

½

p

1

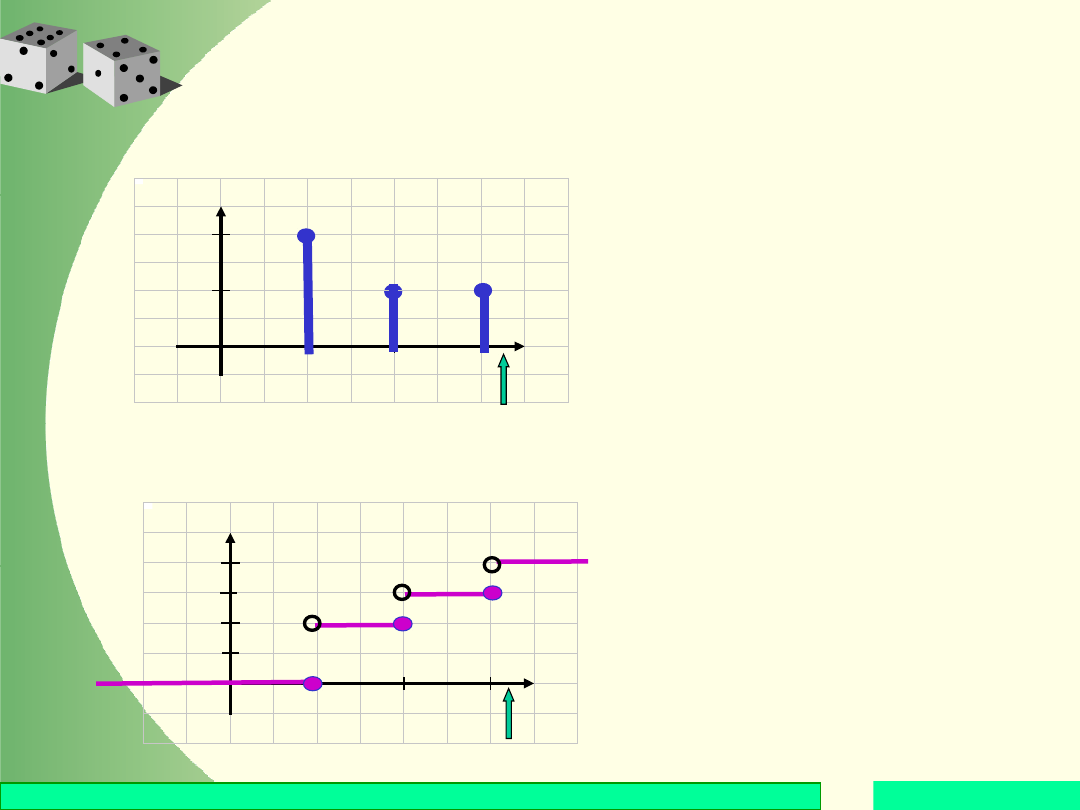
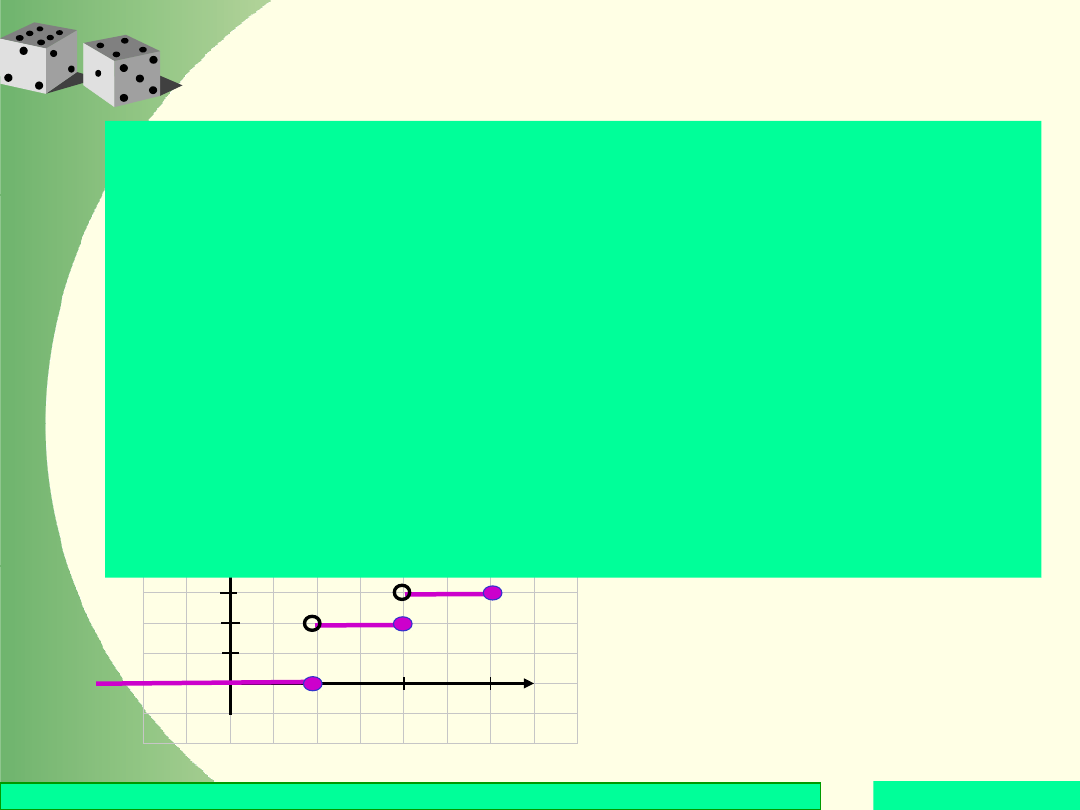
Gdy x > 3, to w
przedziale (–; x) są

trzy punkty skokowe,
którym odpowiada
łączne
prawdopodobieństwo 1
zatem F(x) = 1.

1 4 4 4 4 4 2 4 4 4 4 4 3

Slajd 27 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

1

2

3

X

½

p

1

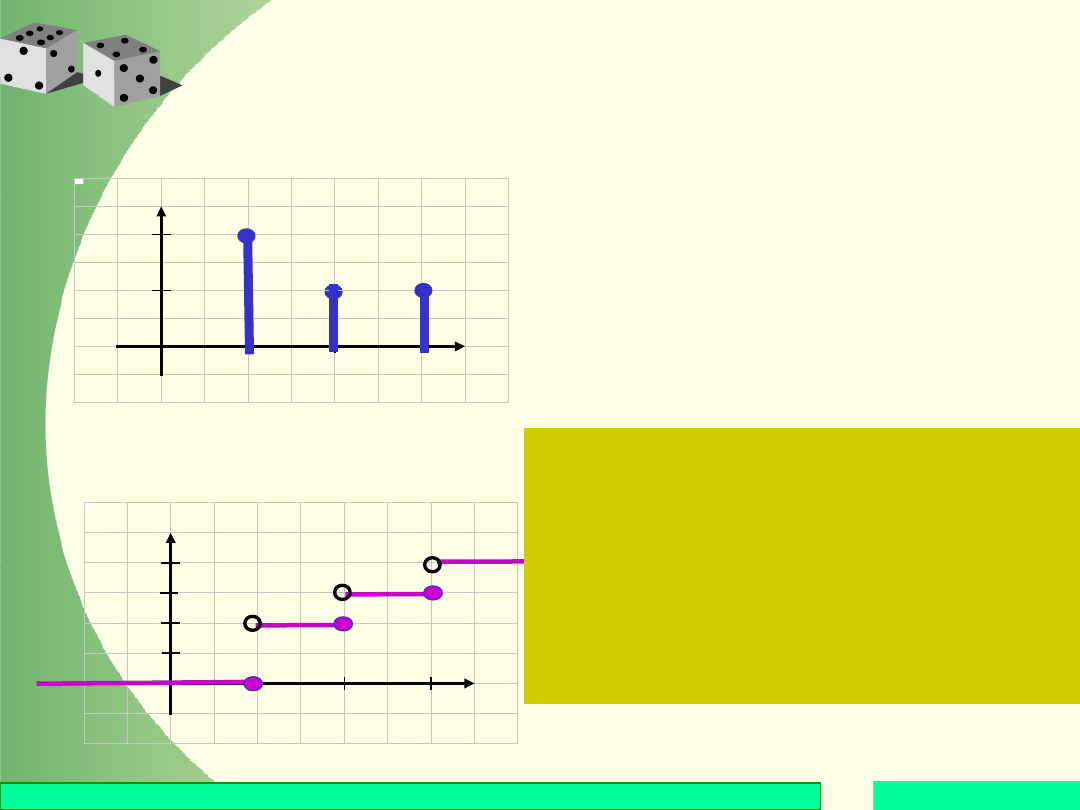
Zauważmy, że dystrybuanta zmiennej losowej
skokowej jest funkcją skokową (schodkową).
Dystrybuanta jest wszędzie ciągła z wyjątkiem
punktów skokowych. W każdym punkcie
skokowym zachodzi warunek

co można zinterpretować następująco: Skok
wartości funkcji w punkcie x

k

odpowiada

prawdopodobieństwu p

k

.

lim ( )

( )

k

k

x xk

p

F x

F x

+

�

=

-

Slajd 28 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Uwaga

Histogram
rozkładu:

1

2

3

X

¼

½

p

Dystrybuanta
rozkładu:

1

2

3

X

½

p

1

1,

1

1

2,

1

2

2

3,

1

,

1

2

1

0

dla

dla

dla

( )

...........

..........

dla

...

1

dla

.

n

n

n

n

x x

p

x

x x

p

p

x

x x

F x

x

x x

p

p

p

x x

-

-

�

�

�

< �

�

�

+

< �

�

=�

�

�

< �

+ + +

�

>

�

�

Załóżmy, że X jest zmienną
losową przyjmującą skończoną
liczbę wartości,
uszeregowanych rosnąco: x

1

,

x

2

, …,x

n

z

prawdopodobieństwami p

1

, p

2

,

…,p

n

.

Wówczas:

Slajd 29 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład a dystrybuanta

Funkcja rozkładu prawdopodobieństwa zmiennej
losowej skokowej X i jej dystrybuanta są ze sobą
ściśle związane.

Na podstawie funkcji rozkładu można określić
dystrybuantę oraz na odwrót: na podstawie
dystrybuanty można wyznaczyć rozkład zmiennej.

Slajd 30 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

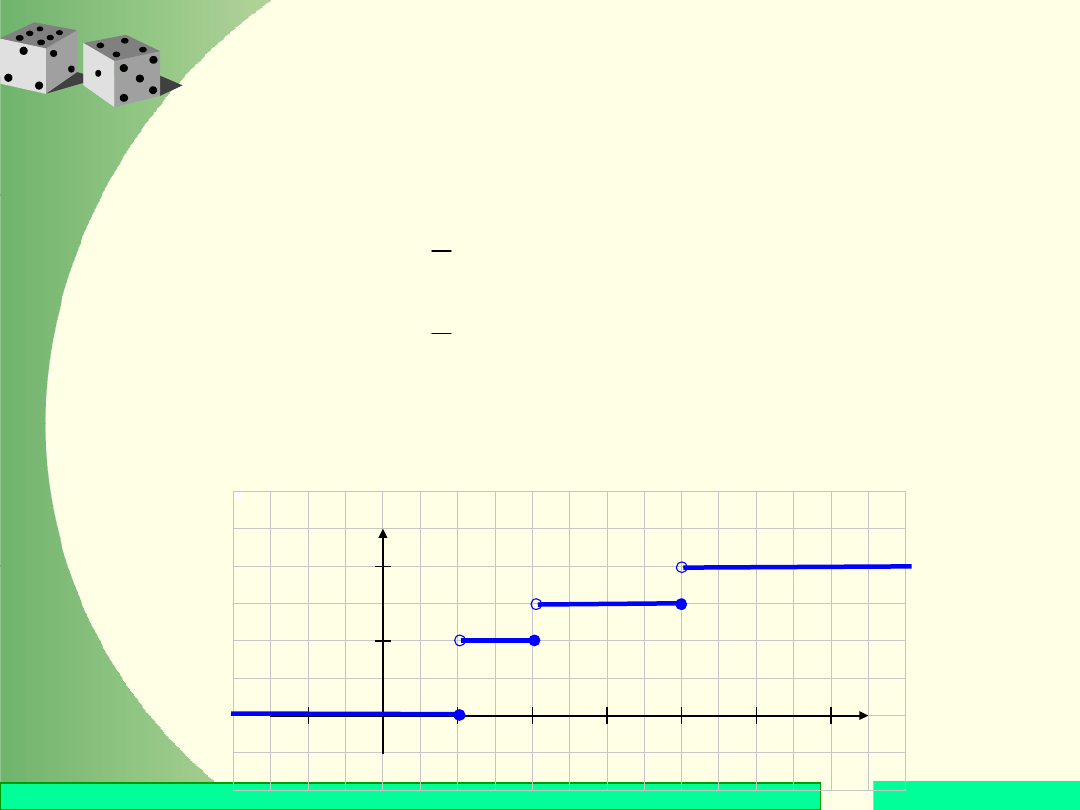
Przykład

Dana jest dystrybuanta pewnej zmiennej losowej
skokowej X:

( )

0

dla

1,

1

dla 1

2,

2
3

dla 2

4,

4

1

dla

4.

x

x

F x

x

x

�

�

�

�

< �

�

=�

�

< �

�

�

>

�

Sporządzić wykres tej dystrybuanty. Wyznaczyć
rozkład zmiennej X i sporządzić jego histogram.

-1

1

2

3

4

5

6

X

p

½

1

Slajd 31 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

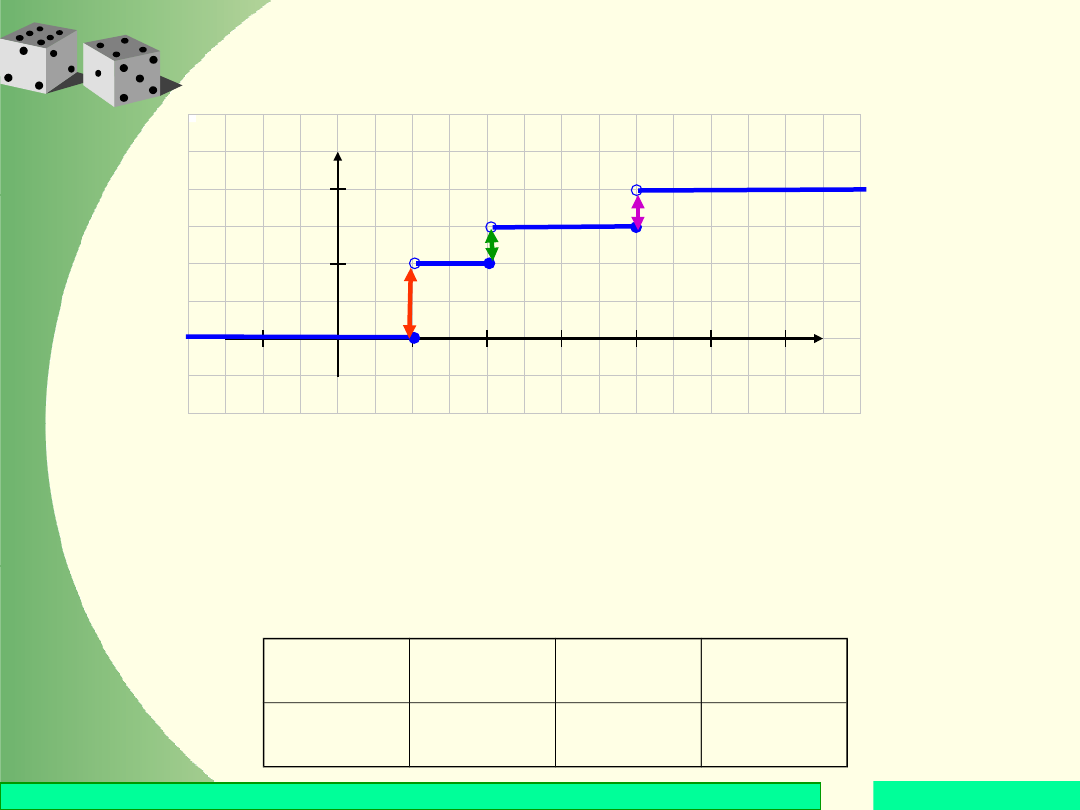
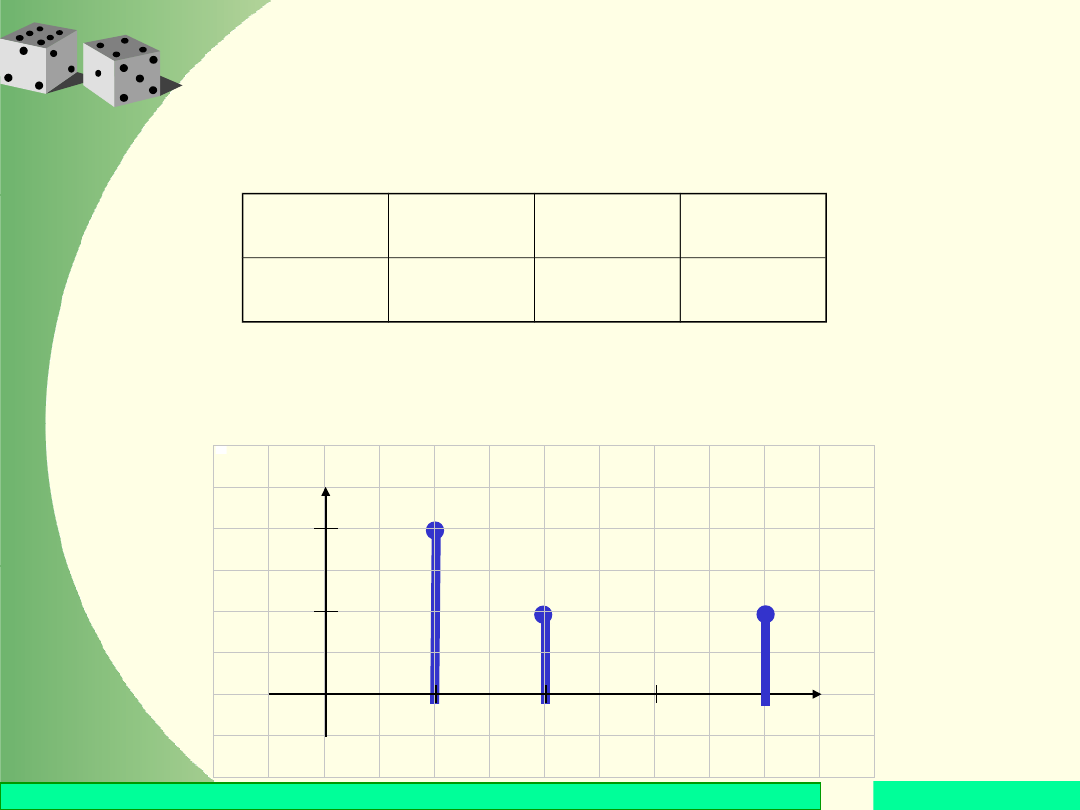
Przykład

-1

1

2

3

4

5

6

X

p

½

1

Punktami skokowymi dystrybuanty są: x

1

= 1, x

2

= 2,

x

3

= 4 . Skoki wartości funkcji w tych punktach są

równe prawdopodobieństwom, z jakimi wartości te są
przyjmowane.

x

k

1

2

4

p

k

Rozkład zmiennej X:

Skok
½

½

Skok
¼

¼

Skok
¼

¼

Slajd 32 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

x

k

1

2

4

p

k

Rozkład zmiennej X:

½

¼

¼

1

2

3

4 X

p

½

¼

Histogram
rozkładu:

Slajd 33 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Wartość oczekiwana zmiennej

losowej

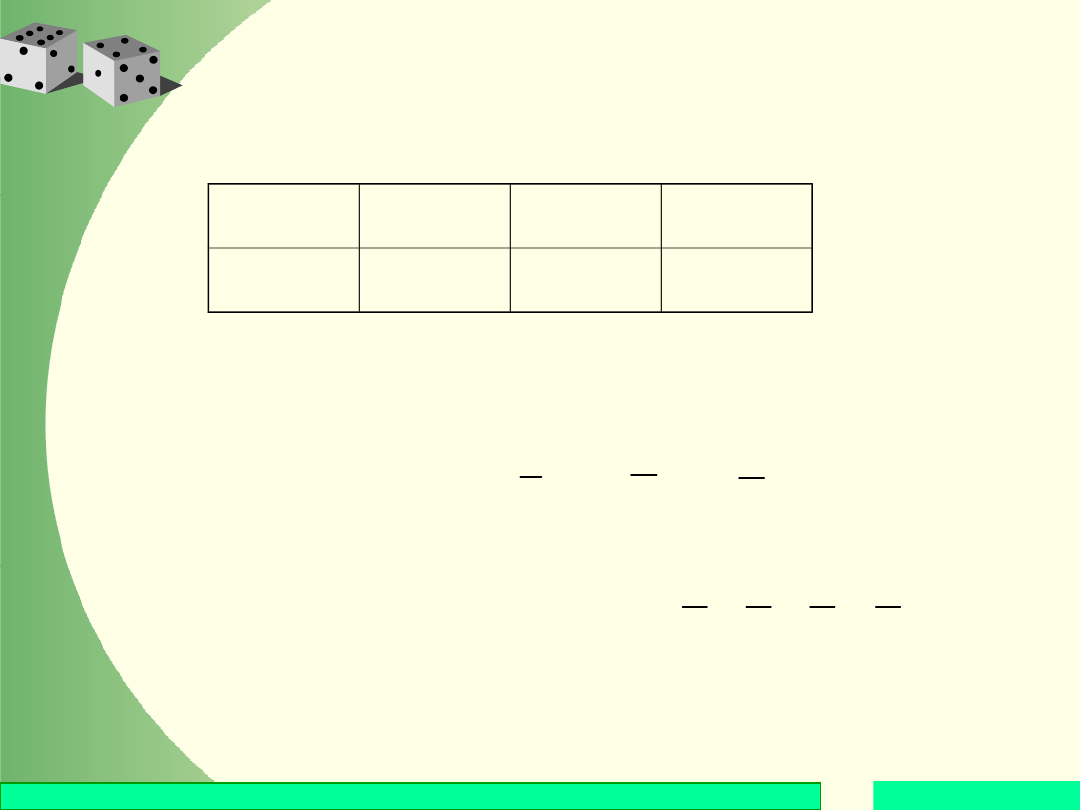
Załóżmy, że X jest zmienną losową przyjmującą wartości
x

1

, x

2

, …,x

n

z prawdopodobieństwami p

1

, p

2

, …,p

n

.

Wartością oczekiwaną tej zmiennej nazywamy liczbę
oznaczaną przez E(X) równą

( )

.

k k

k

E X

x p

=

�

Slajd 34 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

½

¼

¼

Obliczyć E(X). Zinterpretować tę liczbę na
histogramie.

( )

k k

k

E X

x p

=

=

�

1

1

2

�

1

2

4

+ �

1

3

4

+ � =

2 2 3 7
4 4 4 4

= + + =

Slajd 35 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Rozkład zmiennej losowej X dany jest w postaci
tabelki:

x

k

1

2

3

p

k

½

¼

¼

Obliczyć E(X). Zinterpretować tę liczbę na
histogramie.

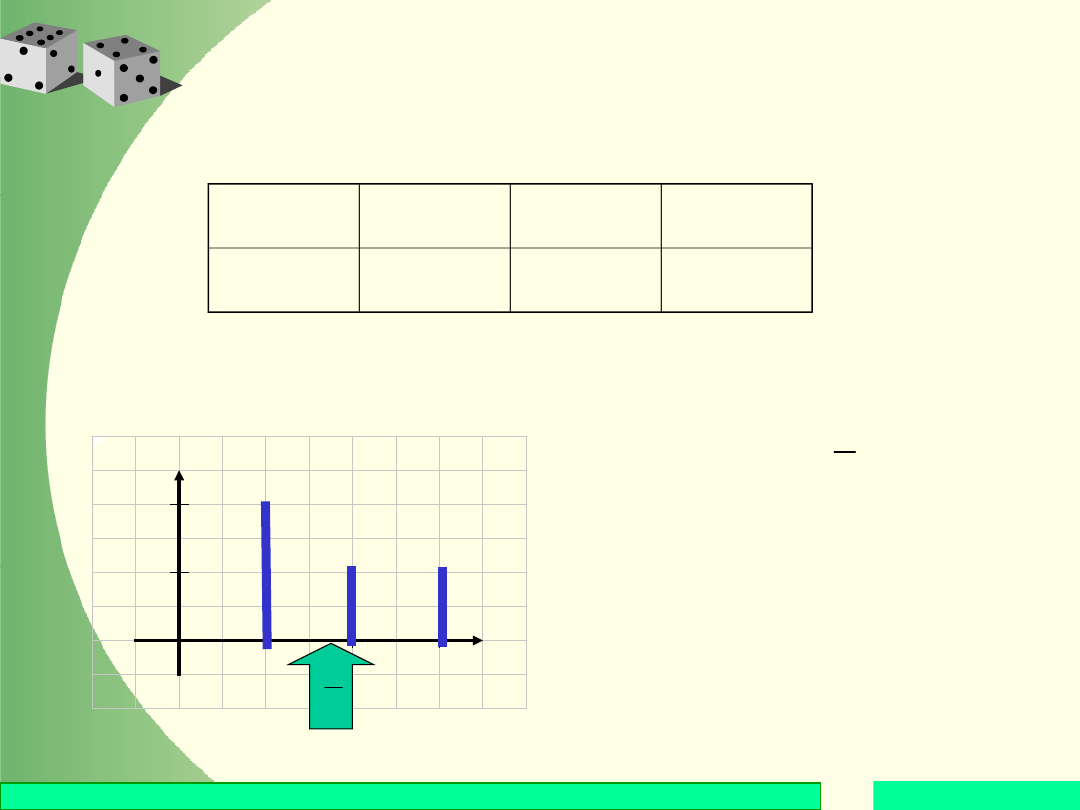
Histogram
rozkładu:

1

2

3

X

¼

½

p

Uwaga.
Liczba E(X) pokazuje, w
którym punkcie osi poziomej
należy podeprzeć histogram,
aby znajdował się on w stanie
równowagi.

7

( )

4

E X =

7

4

Slajd 36 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Własności wartości

oczekiwanej:

Jeżeli X i Y są dowolnymi zmiennymi
skokowymi oraz a i b dowolnymi liczbami, to

E(aX + bY) = a E(X) + b
E(Y).

W
szczególności
:

1. E(a) = a.

2. E(aX) = a E(X).

3. E(aX + b) = a E(X) +
b.

4. E(X + Y) = E(X) +
E(Y).

5. E(X – E(X)) = 0.

Slajd 37 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Wariancja zmiennej

losowej

Liczbę E(X – E(X))

2

nazywamy wariancją

zmiennej X i oznaczamy przez D

2

(X).

Liczba ta jest nieujemna.

Pierwiastek z wariancji nazywamy odchyleniem
standardowym zmiennej losowej X.

Slajd 38 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Wariancja zmiennej

losowej

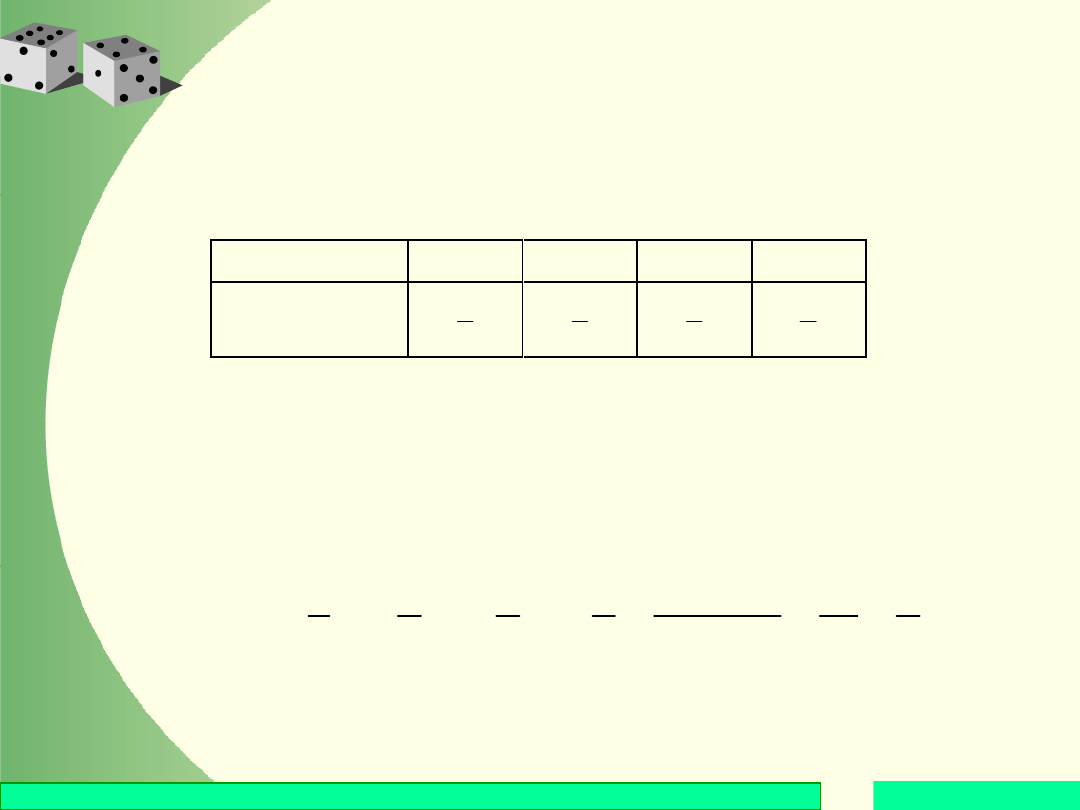
Wariancja zmiennej losowej X wyraża się
wzorem

D

2

(X) = E(X

2

) – (E(X))

2

,

gdzie E(X) oznacza wartość oczekiwaną zmiennej
X ,

a w przypadku zmiennej skokowej:

2

2

(

)

.

k k

k

E X

x p

=

�

Slajd 39 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Wyznaczyć wartość oczekiwaną i wariancję
zmiennej losowej X o rozkładzie danym za pomocą
tabelki:

k

x

0

1

2

3

k

p

1
3

1
4

1
4

1

6

Mnożąc wartości przyjmowane przez zmienną losową
skokową przez odpowiednie prawdopodobieństwa, a
następnie sumując tak otrzymane iloczyny mamy

1

1

1

1 3 6 6 15 5

( ) 0

1

2

3

3

4

4

6

12

12 4

E X

+ +

= � + � + � + � =

=

=

Slajd 40 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Wyznaczyć wartość oczekiwaną i wariancję
zmiennej losowej X o rozkładzie danym za pomocą
tabelki:

k

x

0

1

2

3

k

p

1
3

1
4

1
4

1

6

Podnosząc do kwadratu każdą z wartości x

k

, mnożąc

przez odpowiednie prawdopodobieństwa, a następnie
sumując tak otrzymane iloczyny mamy

2

2

2

2

2

1

1

1

1 3 12 18 33 11

(

) 0

1

2

3

.

3

4

4

6

12

12

4

E X

+ +

= � + � + � + � =

=

=

(

)

2

2

2

2

11

5

44 25 19

( )

(

)

( )

( )

.

4

4

16

16

D X

E X

E X

-

=

-

= -

=

=

Tym samym

Slajd 41 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Własności wariancji

Jeżeli X jest dowolną zmienną skokową oraz a i
b dowolnymi liczbami, to

1. D

2

(a) = 0.

2. D

2

(aX) = a

2

D

2

(X).

3. D

2

(aX + b) = a

2

D

2

(X).

4. D

2

(X + Y) = D

2

(X) +

D

2

(Y).

Jeżeli X i Y są dowolnymi niezależnymi
zmiennymi skokowymi, to

Slajd 42 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład zero-jedynkowy

Zmienna losowa X ma rozkład zero-jedynkowy,
jeżeli przyjmuje dwie wartości: x

1

= 1 i x

2

= 0 z

prawdopodobieństwami odpowiednio: p

1

= p, p

2

= 1–

p.

( )

E X

p

=

2

( )

(1

)

D X

p

p

=

-

Slajd 43 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

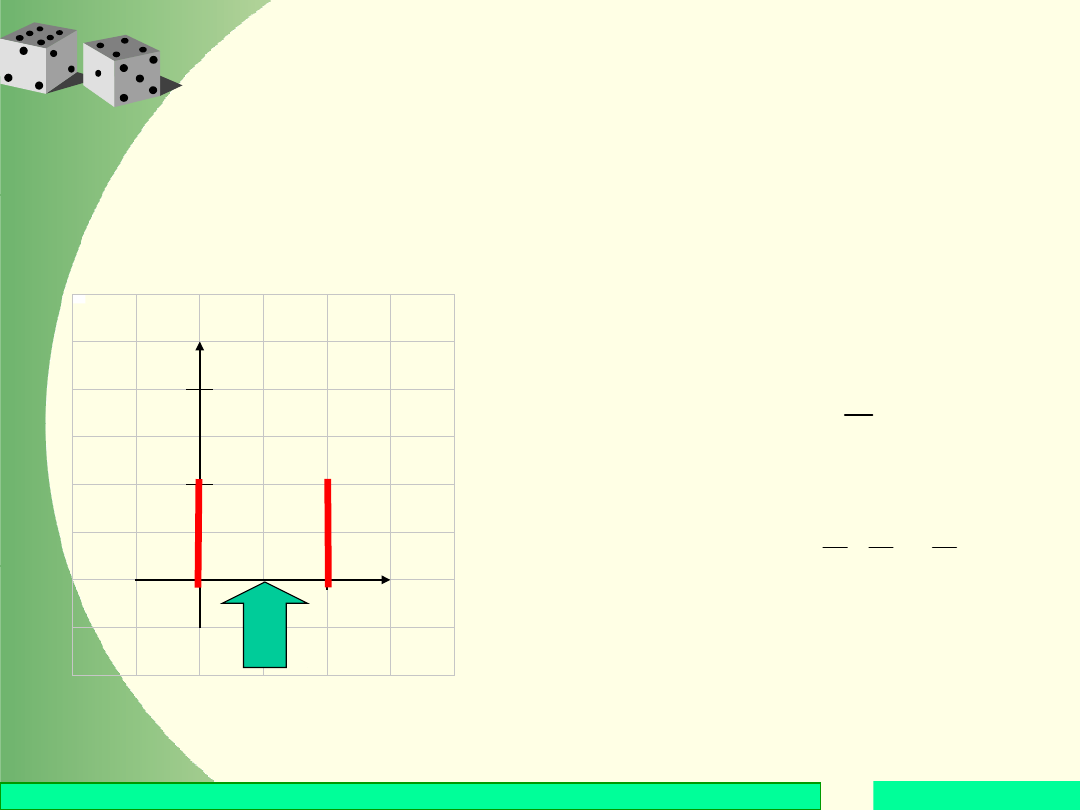
Rozkład zero-jedynkowy

1 X

0

½

Taki rozkład ma np. zmienna przypisana
jednokrotnemu rzutowi symetryczną monetą i
przyjmująca wartość 0, gdy wypadła reszka, oraz
wartość 1, gdy wypadł orzeł. Wtedy p = 1 – p = ½.

1

( )

2

E X

p

= =

2

1 1 1

( )

(1

)

2 2 4

D X

p

p

=

-

= � =

½

Slajd 44 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład Bernoulli’ego

Zmienna losowa X ma rozkład Bernoulli’ego o
parametrach n i p, jeżeli przyjmuje ona wartości x

k

= 0, 1, 2, 3, …, n z prawdopodobieństwami:

(

)

(1

)

k

n k

k

n

p

P X k

p

p

k

-

� �

=

= =

� � -

� �

� �

Taki rozkład ma zmienna losowa przyjmująca
wartości równe liczbie sukcesów w schemacie n
prób Bernoulli’ego.     .

E X

np

( ) 

D X

np

p

2

1

( )

(

)





Slajd 45 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

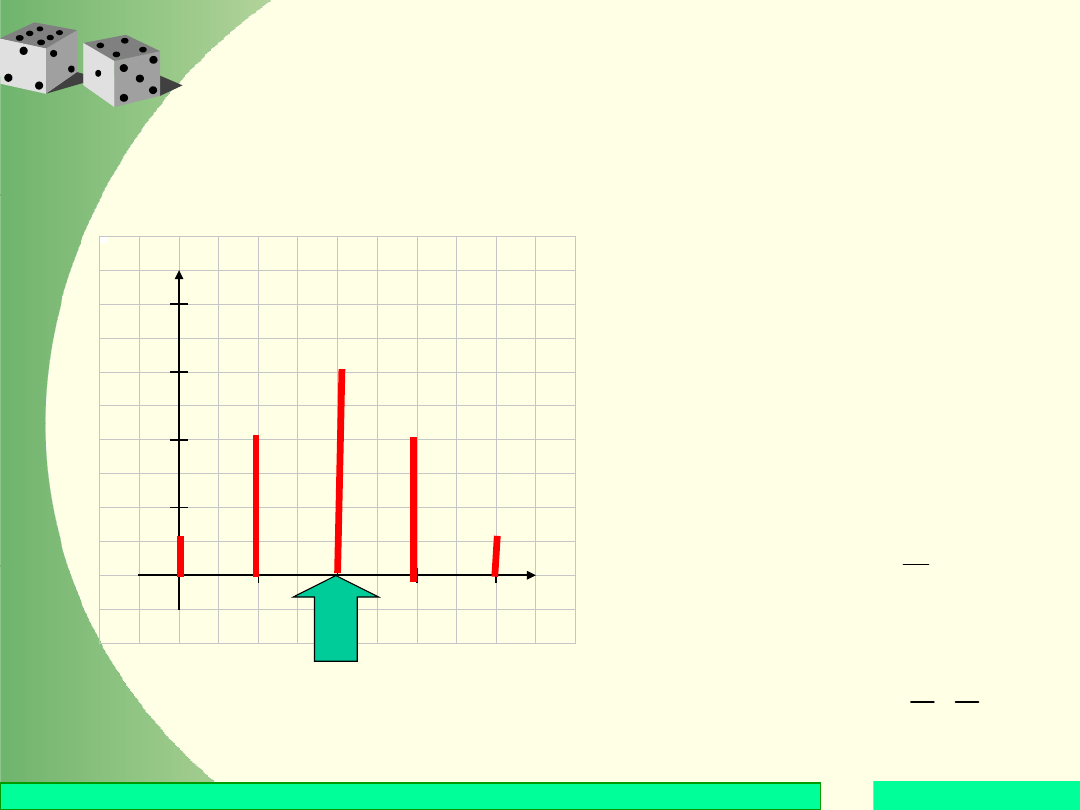
Rozkład Bernoulli’ego

1

2

3

4 X

p

0

2

Histogram rozkładu
przy n = 4 i p = ½.

1

( )

4

2

2

E X

np

=

= � =

2

1 1

( )

(1

) 4

1

2 2

D X

np

p

=

-

= � � =

Slajd 46 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład Poissona

Zmienna losowa X ma rozkład Poissona o
parametrze



> 0, jeżeli przyjmuje wartości x

k

= 0, 1,

2, 3, …, n, … z prawdopodobieństwami

(

)

.

!

k

k

p

P X k

e

k

l

l

-

=

= =

�





)

(X

E





)

(

2

X

D

Slajd 47 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

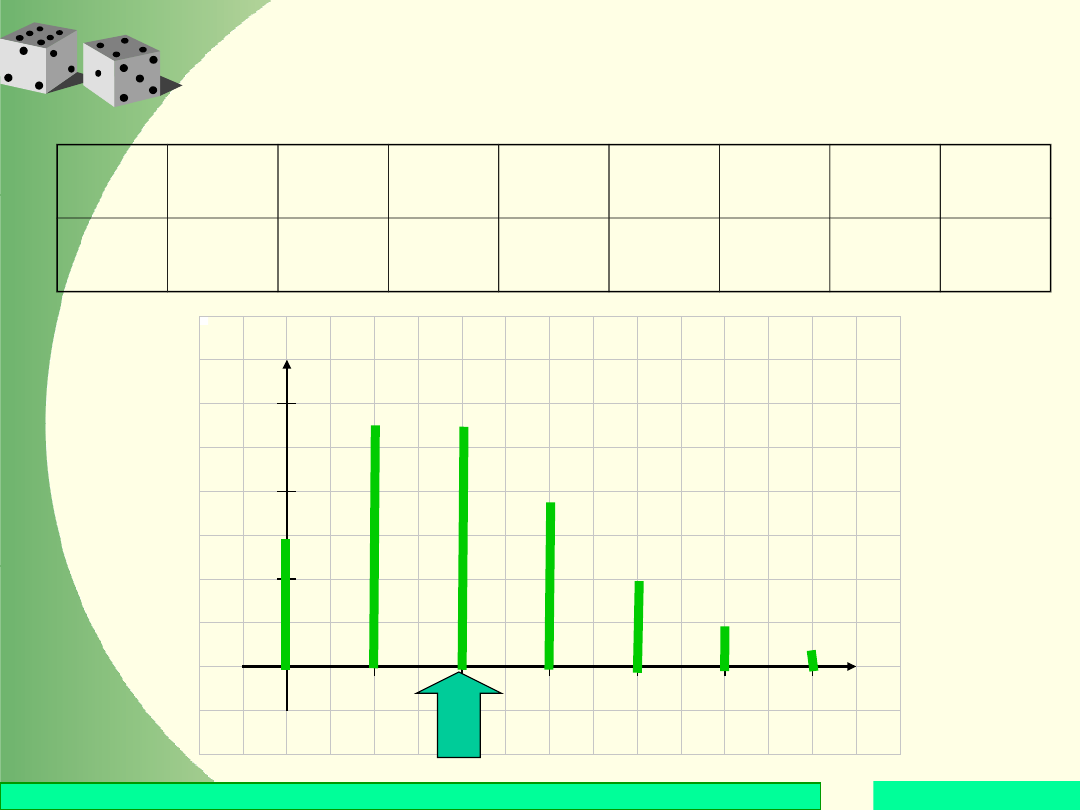
Rozkład Poissona

Liczbę dzieci, które rodzą się określonego dnia w
pewnym mieście N, można opisać zmienną losową X o
rozkładzie Poissona o parametrze



= 2. Sporządzić

histogram rozkładu. Podać wartość oczekiwaną i
wariancję liczby urodzin.

2

2

(

)

.

!

k

k

p

P X k

e

k

-

=

= =

�

Ponieważ



= 2, to

Podstawiając w tym wzorze kolejno k = 0, 1, 2, 3, … i
przyjmując

___________

otrzymamy

2

0,1353

e

-

=

x

k

0

1

2

3

4

5

6

…

p

k

0,14 0,27 0,27 0,18 0,09 0,04 0,01

...

Slajd 48 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład Poissona

x

k

0

1

2

3

4

5

6

…

p

k

0,14 0,27 0,27 0,18 0,09 0,04 0,01

...

1

2

3

4

5

6 X

p

0

0,1

0,2

2

( )

2

E X

l

= =

2

( )

2

D X

l

= =

Slajd 49 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Rozkład Bernoulli’ego a rozkład

Poissona

Dla dużych n występuje zbieżność rozkładu
Bernoulliego do rozkładu Poissona z parametrem 

!

k

e

q

p

k

n

k

k

n

k























gdzie  = np.
Przybliżenie to jest w miarę dokładne, gdy n  50

(czasem przyjmuje się, że n  100 ) i p  0,1 oraz 

= np  10.

Slajd 50 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

Obliczyć prawdopodobieństwo wylosowania co najwyżej
trzech osób leworęcznych w 200 losowaniach, jeśli
wiadomo, że prawdopodobieństwo spotkania osoby
leworęcznej w pewnej populacji ludzi wynosi 0,05.

Ponieważ n = 200  50 , p = 0,05  0,1 oraz  = np

=10  10, to można przyjąć, że mamy tu do

czynienia z rozkładem Poissona.

(

)

(

)

(

)

(

)

(

)

0

3

0

1

2

3

P

k

P k

P k

P k

P k

� � =

= +

= +

= +

=

(

)

,

!

k

P k

e

k

l

l

l

-

=

czyli

(

)

10

10

,10

!

k

P k

e

k

-

=

Slajd 51 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe

Przykład

(

)

0

1

2

3

10

10

10

10

10

10

10

10

0

3

0!

1!

2!

3!

P

k

e

e

e

e

-

-

-

-

� � =

+

+

+

=

10

10

10

10

10

10

10

10

100

1000

500

10

10

50

2

6

3

e

e

e

e

e

e

e

e

-

-

-

-

-

-

-

-

=

+

+

+

=

+

+

+

=

10

10

683

683

683

683

0,011

3

3 20589 61767

3

e

e

-

=

=

�

=

�

�

�

Ostatecznie szukane prawdopodobieństwo wylosowania co
najwyżej trzech osób leworęcznych wynosi 0,011.

Slajd 52 / 52

Tomasz Kowalski. Matematyka. Wykład 23. Zmienne losowe

skokowe