1
Politechnika Krakowska im. Tadeusza Kościuszki Katedra Automatyki
i Technik Informacyjnych (E-3)
Automatyka
Laboratorium
– Badanie charakterystyk czasowych liniowych układów
regulacji ciągłej –
1. Cel ćwiczenia
Zapoznanie się z podstawowymi obiektami dynamicznymi i z ich odpowiedziami na skok
jednostkowy 1( ).
2. Terminy i podstawowe obiekty dynamiczne
Do analizy i syntezy ukłądów sterowania konieczna jest znajomość modeli matematycznych
obiektów dynamicznych wchodzących w skład danych układów. Model matematyczny można
otrzymać na drodze obróbki informacji zdobytej w trakcie doświadczeń na obiekcie. Model obiektu
jest tym lepszy, im dokładniej odzwierciedla procesy zachodzące w obiekcie w sensie jakościowym
i ilościowym. W opisie brane są pod uwagę obiekty, które można opisać za pomocą liniowych równań
różniczkowych zwyczajnyc o stałych współczynnikach:
( )
+ ⋯ +
( )
+
( ) =
( )
+ ⋯ +
( )
+
( ),
(1)
przy czym ( ) jest wejsćiem na obiekt, a ( )jest wyjściem obiektu, natomiast ≥
.
Jest to model stacjonarny (parametry
,
, …,
i
,
, …, nie zmieniają swoich
wartości w czasie) oraz liniowy (nie występują funkcje, np. pierwiastkowe lub kwadratowe).
W opisie będą brane pod uwagę tylko obiekty o jednym wejściu i jednym wyjściu, tak jak
to zostało przedstawione na rysunku poniżej.
2
Rys. 1. Obiekt o jednym wejściu i jednym wyjściu.
Transmitancja operatorowa jest stosunkiem transformaty Laplace’a sygnału wyjsciwego
do transformaty Laplace’a sygnału wejściowego przy zerowych warynkach początkowych.
( ) =
( )
( )
=
{ ( )}
{ ( )}
=
(
⋯
)
(
⋯
)
,
(2)
przy czym {⋯ } oznacza transformatę Laplace’a, ( ) jest sygnałem wyjściowym obiektu
w dziedzinie czasu , natomiast ( )jest sygnałem wejściowym obiektu w dziedzinie czasu . ( )
i ( ) oznaczają sygnały wejścia i wyjścia, ale poddane już transformacie Laplace’a.
Do badania obiektów będzie używany sygnał skoku jednostkowego 1( ) , który jest
zdefiniowany w sposób:
( ) = 1( ) ≝
1
≥ 0
0
< 0
.
(3)
2.1. Obiekt proporcjonalny
Obiekt proporcjonalny opisany jest równaniem różniczkowym:
( ) =
( ),
(4)
przy czym ( ) jest wyjściem obiektu, a ( ) wejściem na obiekt w dziedzinie czasu. Parametr jest
wzmocnieniem obiektu proporcjonalnego.
Transmitancja obiektu proporcjonalnego ma postać:
( ) = .
(5)
Odpowiedź na skok jednostkowy można zapisać jako:
( ) =
∗ 1( ).
(6)
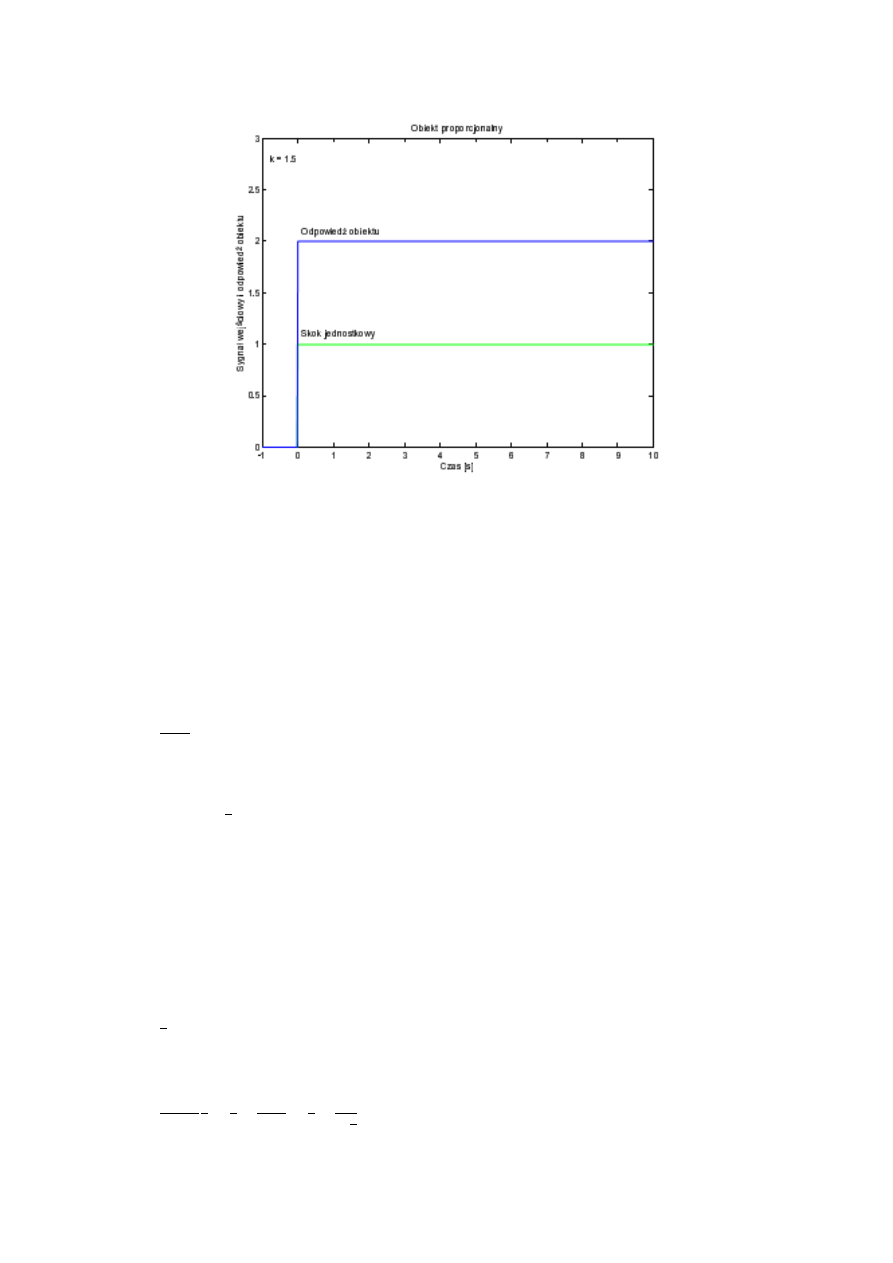
Rysunek zamieszczony poniżej zawiera wykresy skoku jednostkowego 1( ), który jest podawany
na wejście obiektu, oraz odpowiedzi obiektu proporcjonalnego na tego typu wymuszenie.
3
Rys. 2. Odpowiedź obiektu proporcjonalnego na skok jednostkowy 1(t).
2.2. Obiekt inercyjny I-rzędu
Obiekt inercyjny opisany jest równaniem różniczkowym:
̇( ) + ( ) =
( ),
(7)
przy czym to stałą czasowa, natomiast to wzmocnienie obiektu.
Transmitancję obiektu inercyjnego można zapisać jako:
( ) =
,
(8)
Odpowiedź na skok jednostkowy można zapisać jako:
( ) =
1 −
.
(9)
Teraz zostanie przedstawiony sposób obliczania odpowiedzi obiektu na skok jednostkowy. Ze wzoru
(2) wynika, że:
( ) = ( ) ∗ ( ).
(10)
Jeżeli na wejście podawany jest skok jednostkowy 1( ), to korzystając z tablic transformaty Laplace’a
(załącznik 1), można zapisać, że:
( ) = .
(11)
Wstawiając wzory (8) i (11) do wzoru (10) można otrzymać równość:
( ) =
(
)
= −
= −
.
(12)
4
Stosując odwrotną transformatę Laplace’a, czyli przechodząc z dziedziny operatora do dziedziny
czasy , otrzymuje się wzór (9).
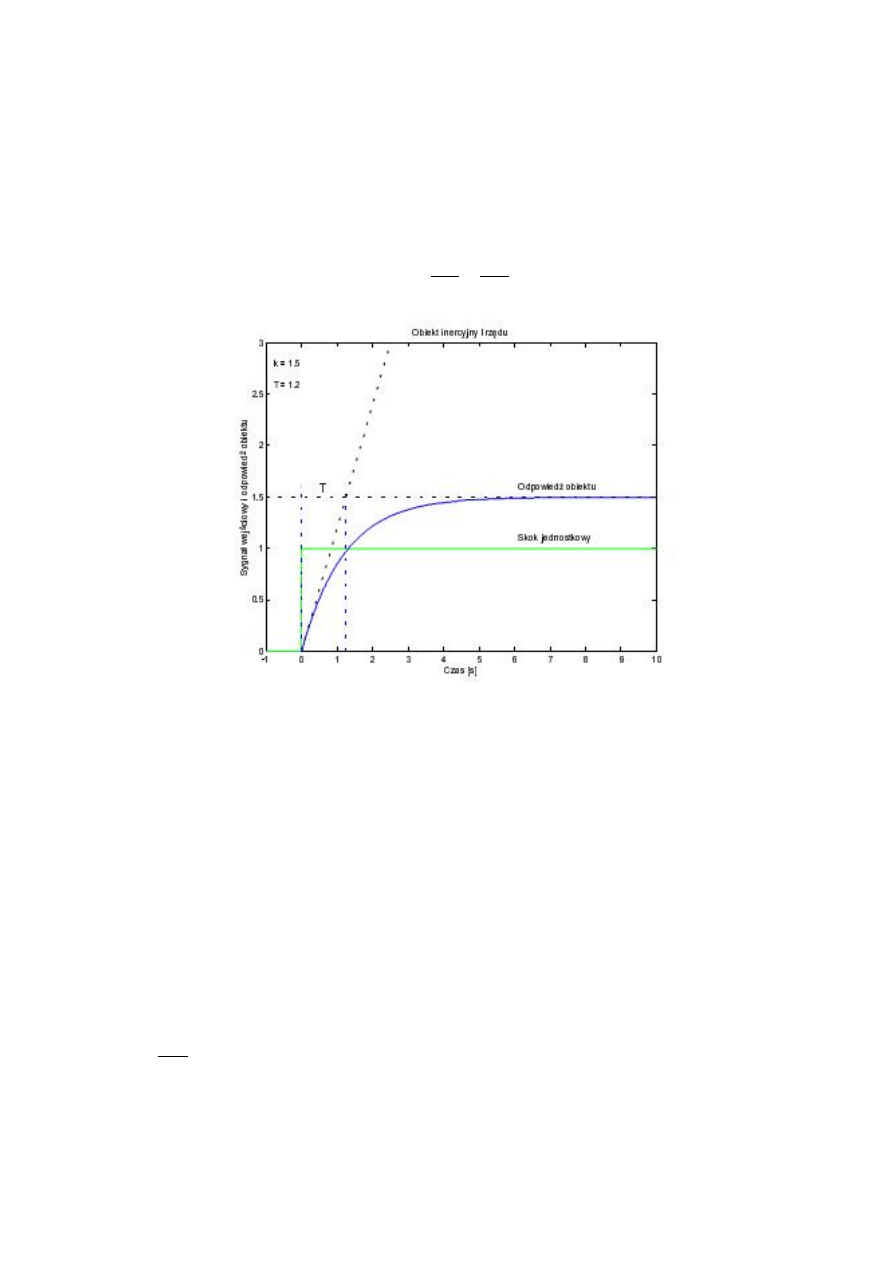
Rys. 3. przedstawia odpowiedź obiektu inercyjnego I-rzędu na skok jednostkowy 1( ).
Wykres odpowiedzi dochodzi do wartości ustalonej, przy czym przyjmuje się, że przebieg odpowiedzi
na skok jednostkowy 1( ) ustalił się, gdy różnica między wartością chwilową a ustaloną mieści się
w granicach 3 − 5%. Znając wartość ustaloną oraz wartość skoku jednostkowego, można wyliczyć
wzmocnienie obiektu korzystając ze wzoru: =
(∞)
(∞)
=
(∞)
( )
.
Rys. 3. Odpowiedź obiektu inercyjnego I-rzędu na skok jednostkowy 1(t).
Stała czasowa jest to czas, po którym proces osiągnąłby wartość ustaloną, gdyby odpowiedź
narastała ze stałąi maksymalną prędkością równą prędkości początkowej. Stałą czasową można
odczytać z wykresu na dwa sposoby:
1. Przez narysowanie stycznej w punkcie początkowym przebiegu odpowiedzi na skok
jednostkowy. Punkt przecięcia stycznej z linią oznaczającą wartość ustaloną wyznacza stałą
czasową . Ten sposób został ukazany na rys. 3.
2. Przez znalezienie punktu, w którym odpowiedź obiektu inercyjnego I-rzędu osiągnie wartość
0,637
wartości
ustalonej.
Przyjmując
=
we
wzorze
(9)
otrzymuje
się,
że ( ) = (1 −
) z czego wynika ( ) = 0,632
2.3. Obiekt różniczkujący idealny
Obiekt różniczkujący idealny opisany jest równaniem różniczkowym:
( ) =
( )
.
(13)
Transmitancję obiektu różniczkującego idealnego można zapisać jako:
( ) = .
(14)
5
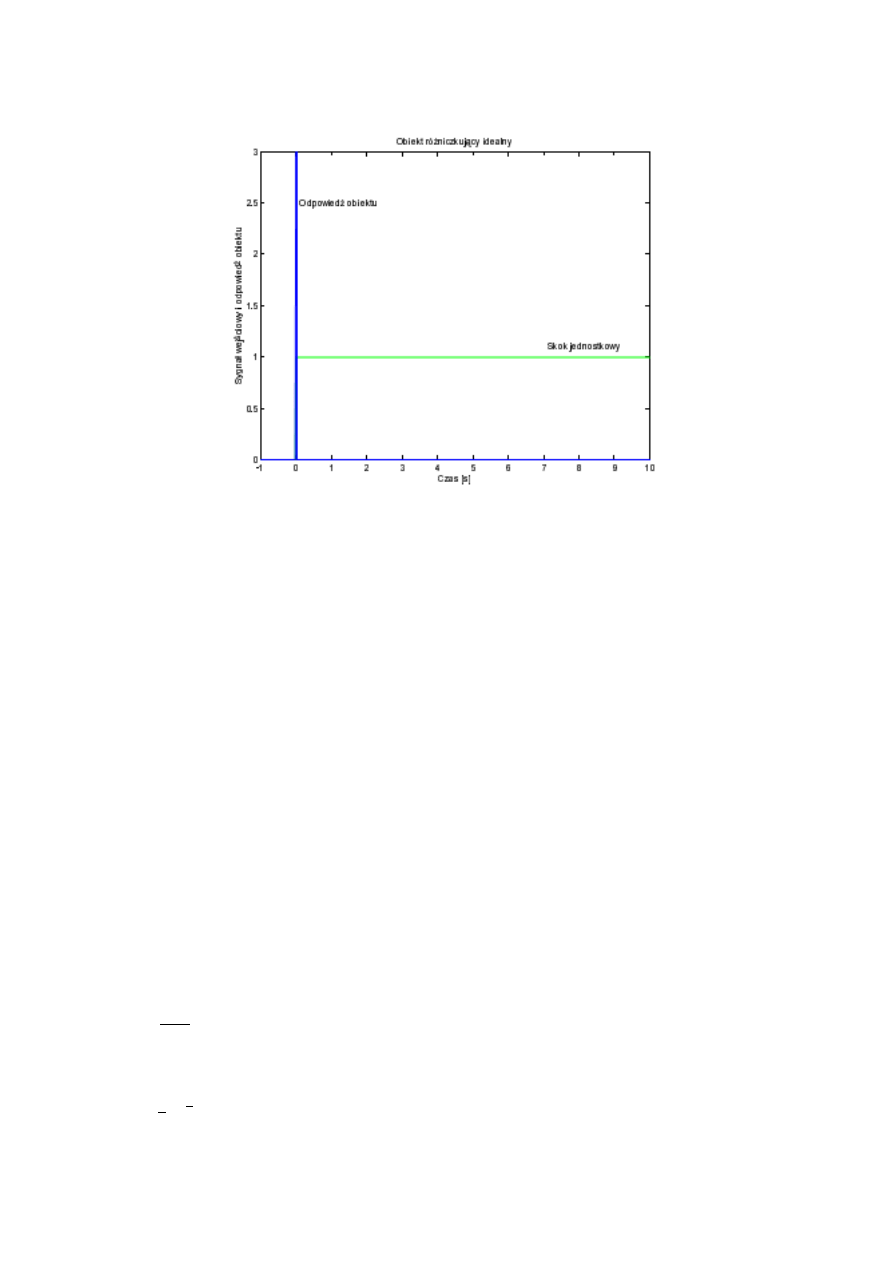
Rys. 4. Odpowiedź obiektu różniczkującego idealnego na skok jednostkowy 1(t).
Odpowiedzią obiektu różniczkującego idealnego na skok jednostkowy 1( ) jest impuls jednostkowy
( )
( ) = ( ),
(15)
Który posiada dwie własności:
( ) ≝
∞
= 0
0
| | > 0
,
(16)
oraz
∫
( )
∞
= 1 .
(17)
2.4. Obiekt różniczkujący z inercją I-rzędu
Obiekt różniczkujący z inercją I-rzędu opisany jest równaniem różniczkowym:
̇( ) + ( ) =
̇( ),
(18)
przy czym jest współczynnikiem wzmocnienia, a stałą czasową.
Transmitancję obiektu różniczkującego z inercją I-rzędu można zapisać jako:
( ) =
.
(19)
Odpowiedź obiektu różniczkującego z inercją I-rzędu na skok jednostkowy 1( ) ma postać:
( ) =
.
(20)
6
Poniżej zostanie przedstawiony sposób obliczania odpowiedzi na skok jednostkowy 1( ) dla obiektu
różniczkującego z inercją I-rzędu. W przypadku tego typu sygnału wejściowego transformata ( ) ma
postać przedstawioną we wzorze (11). Podstawiając wzory na transmitancję dla obiektu
różniczkującego z inercją I-rzędu (19) oraz na skok jednostkowy (11), wyjście w dziedzinie operatora
przyjmuje postać:
( ) =
=
.
(21)
Korzystając z transformaty odwrotnej Laplace’a można zapisać wzór (20), który jest odpowiedzią
w dziedzinie czasu na skok jednostkowy 1( ).
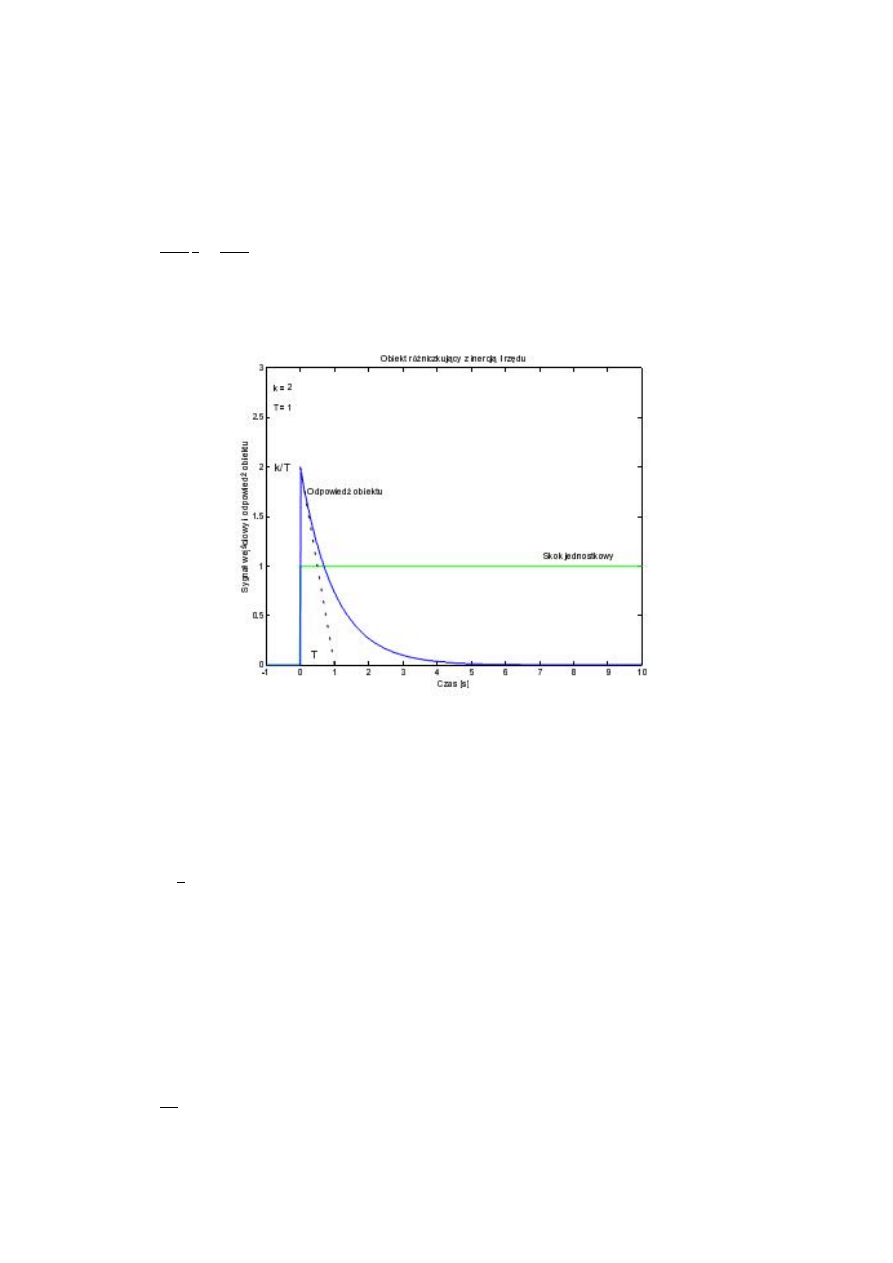
Rys. 5. Odpowiedź obiektu różniczkującego z inercją I-rzędu na skok jednostkowy 1(t).
Wykorzystując wykres odpowiedzi na skok jednostkowy dla tego obiektu można wyznaczyć wartości
i . Wyznaczenie stałej czasowej rozpoczyna się od przeprowadzenia stycznej w punkcie
początkowym odpowiedzi tak, jak to zostało pokazane na rys. 5. Przecięcie stycznej i wartości
ustalonej wyznacza wartość stałej czasowej (w przykładzie na rys. 5. = 1). Następnie można
wyznaczyć z wykresu wartość odpowiedzi w chwili początkowej (w przykładzie wynosi ona 2)
i ze wzoru = 2 można wyliczyć wartość (w przykładzie z rys. 5. = 2).
2.5. Obiekt całkujący idealny
Obiekt całkujący idealny opisany jest równaniem różniczkowym:
̇( ) = ( ),
(22)
przy czym jest stałą całkowania.
Transmitancję obiektu całkującego idealnego można zapisać jako:
( ) =
.
(23)
7
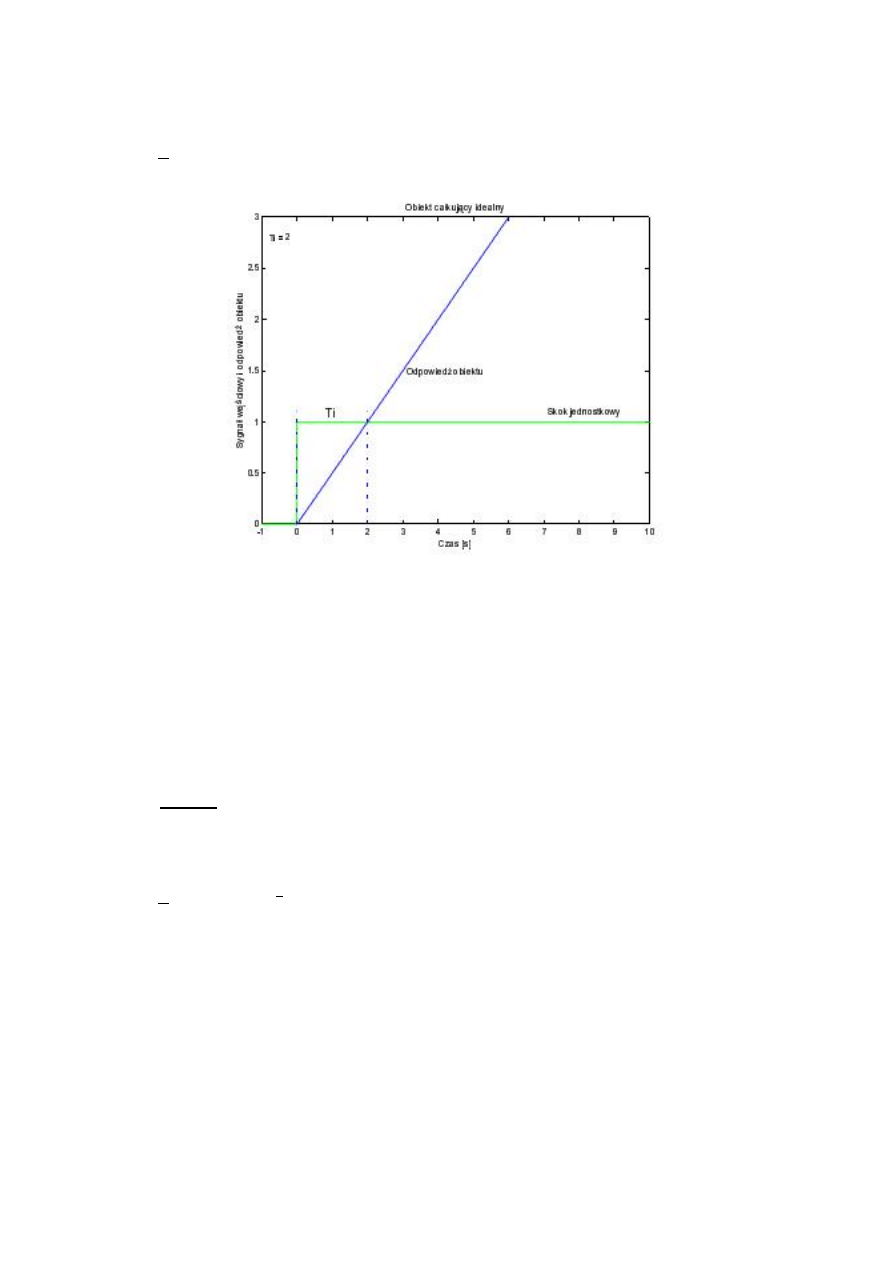
Odpowiedź obiektu całkującego idealnego na skok jednostkowy 1( ) ma postać:
( ) = .
(24)
Rys. 6. Odpowiedź obiektu całkującego idealnego na skok jednostkowy 1(t).
2.6. Obiekt całkujący z inercją I-rzędu
Obiekt całkujący z inercją I-rzędu opisany jest równaniem różniczkowym:
̈( ) +
̇( ) = ( ),
(25)
przy czym jest czasem zdwojenia, a stałą czasową układu.
Transmitancję obiektu całkującego z inercją I-rzędu można zapisać jako:
( ) =
(
)
.
(26)
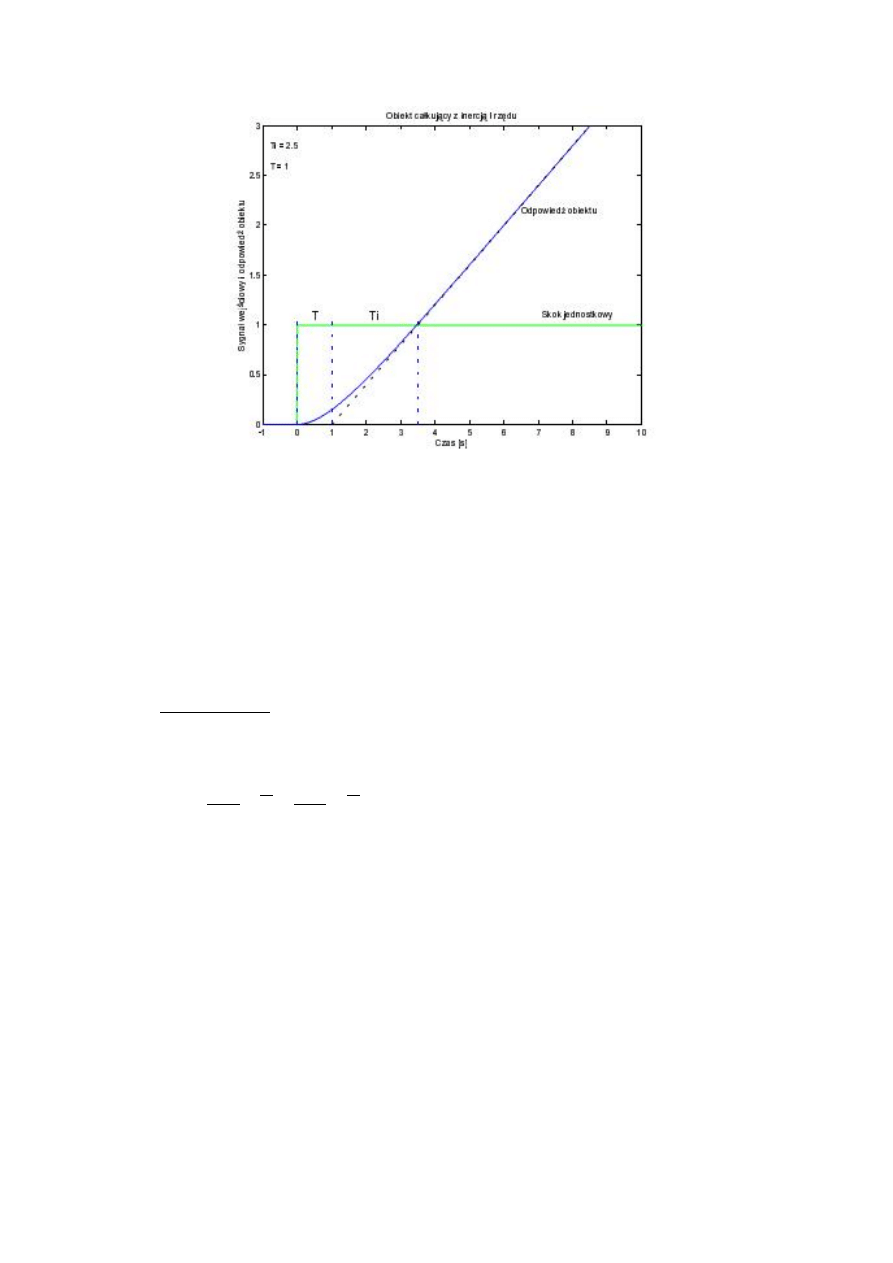
Odpowiedź obiektu całkującego z inercją I-rzędu na skok jednostkowy 1( ) ma postać:
( ) =
−
1 −
.
(27)
8
Rys. 7. Odpowiedź obiektu całkującego z inercją I-rzędu na skok jednostkowy 1(t).
2.7. Obiekt inercyjny II-rzędu
Obiekt inercyjny II-rzędu opisany jest równaniem różniczkowym:
̈( ) + (
+
) ̇( ) + ( ) =
( ),
(28)
przy czym ,
to stałe czasowe, a jest wzmocnieniem.
Transmitancję obiektu inercyjnego II-rzędu można zapisać jako:
( ) =
(
)
.
(29)
Odpowiedź obiektu inercyjnego II-rzędu na skok jednostkowy 1( ) ma postać:
( ) =
1 −
+
.
(30)
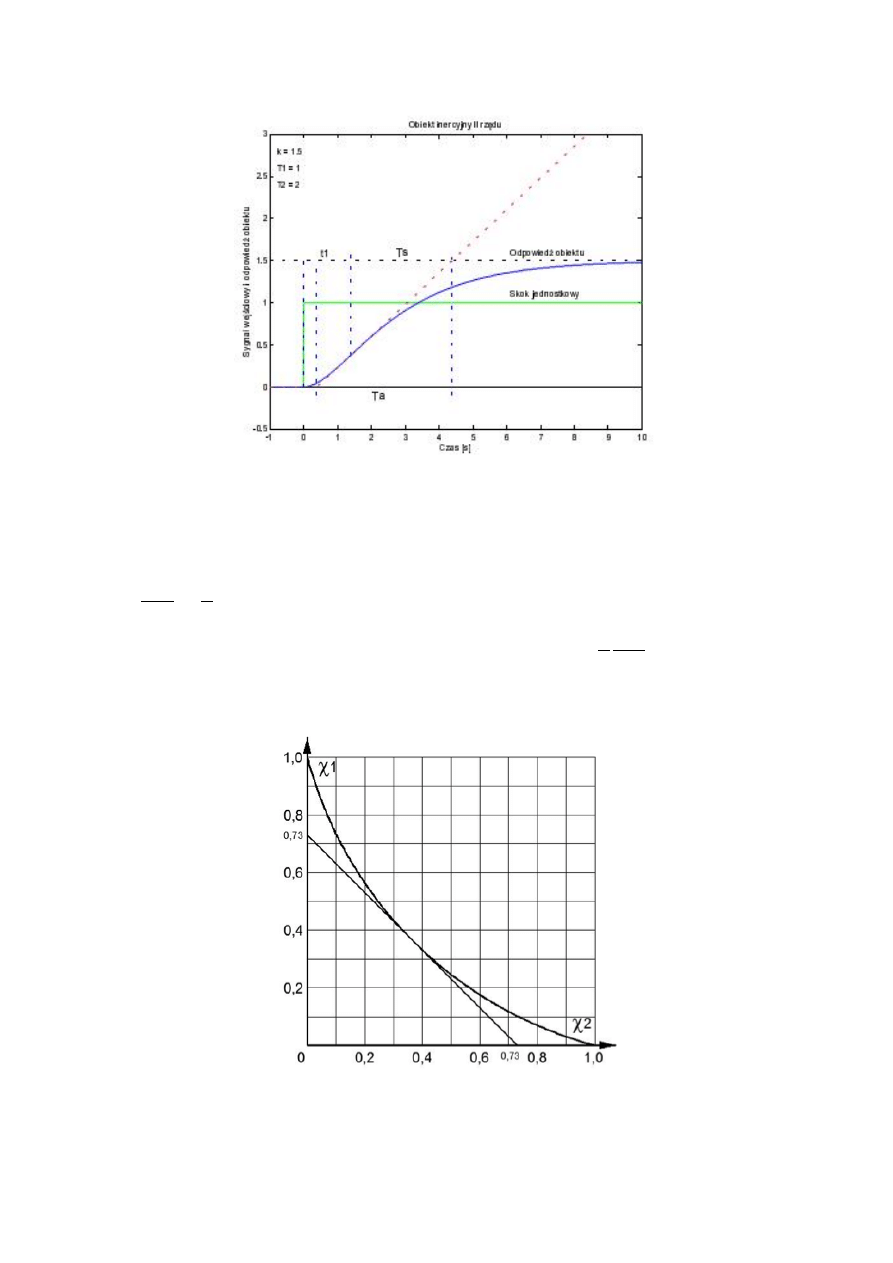
Na wykresie przedstawionym poniżej, zamieszczona została odpowiedź obiektu inercyjnego II-rzędu
na skok jednostkowy 1( ).
9
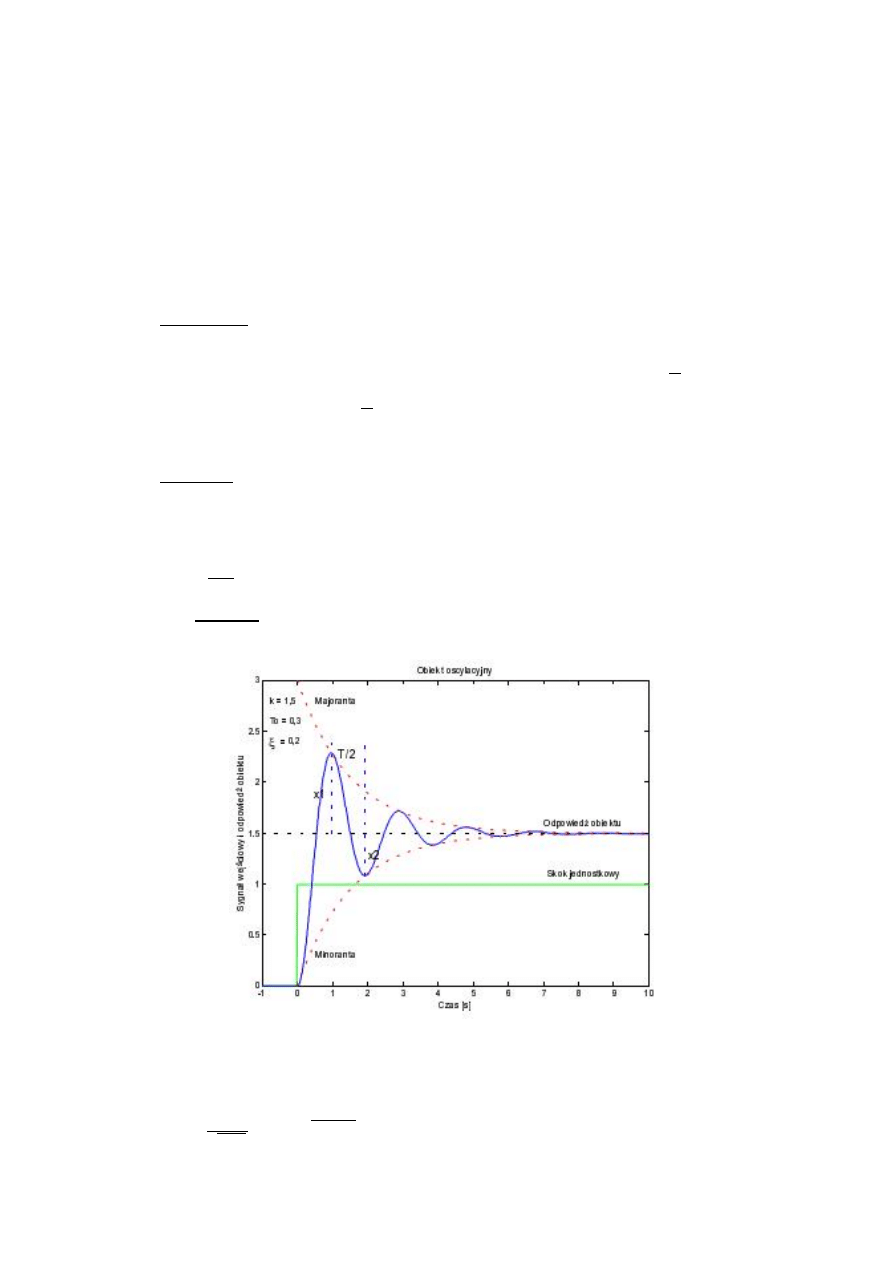
Rys. 8. Odpowiedź obiektu inercyjnego II-rzędu na skok jednostkowy 1(t).
Czas jest czasem, w którym znajduje się punkt przegięcia. Można go obliczyć, po dwukrotnym
różniczkowaniu wzoru (30) i następnie przyrównaniu go do zera, ze wzoru:
=
ln
.
(31)
Natomiast wylicza się ze wzoru
=
+
, a ze wzoru
=
. Korzystając z tych
dwóch równań można obliczyć stałe czasowe obiektu i . Ze względu jednak, iż jest to dość
uciążliwe, korzysta się z tzw. krzywych Oldenburga – Sartoriusa.
Rys. 9. Krzywe Oldenburga - Sartoriusa.
10
2.8. Obiekt oscylacyjny
Obiekt oscylacyjny opisany jest równaniem różniczkowym:
̈ ( ) + 2
̇( ) + ( ) =
( ),
(32)
przy czym
jest wzmocnieniem obiektu,
okresem drgań nietłumionych, natomiast
współczynnikiem tłumienia, 0 ≤
< 1.
Transmitancja obiektu jest równa:
( ) =
.
(33)
Transmitancję (33) można zapisać w innej postaci po podstawieniu oznaczeń
=
– częstotliwość
drgań własnych nietłumionych, =
=
– stała tłumienia. Otrzymana wtedy transmitancja
ma postać:
( ) =
.
(34)
Odpowiedź na skok jednostkowy w dziedzinie czasu można zapisać jako:
( ) =
1 −
( cos
+ sin
) ,
(35)
gdzie:
=
−
jest częstotliwością drgań własnych tłumionych.
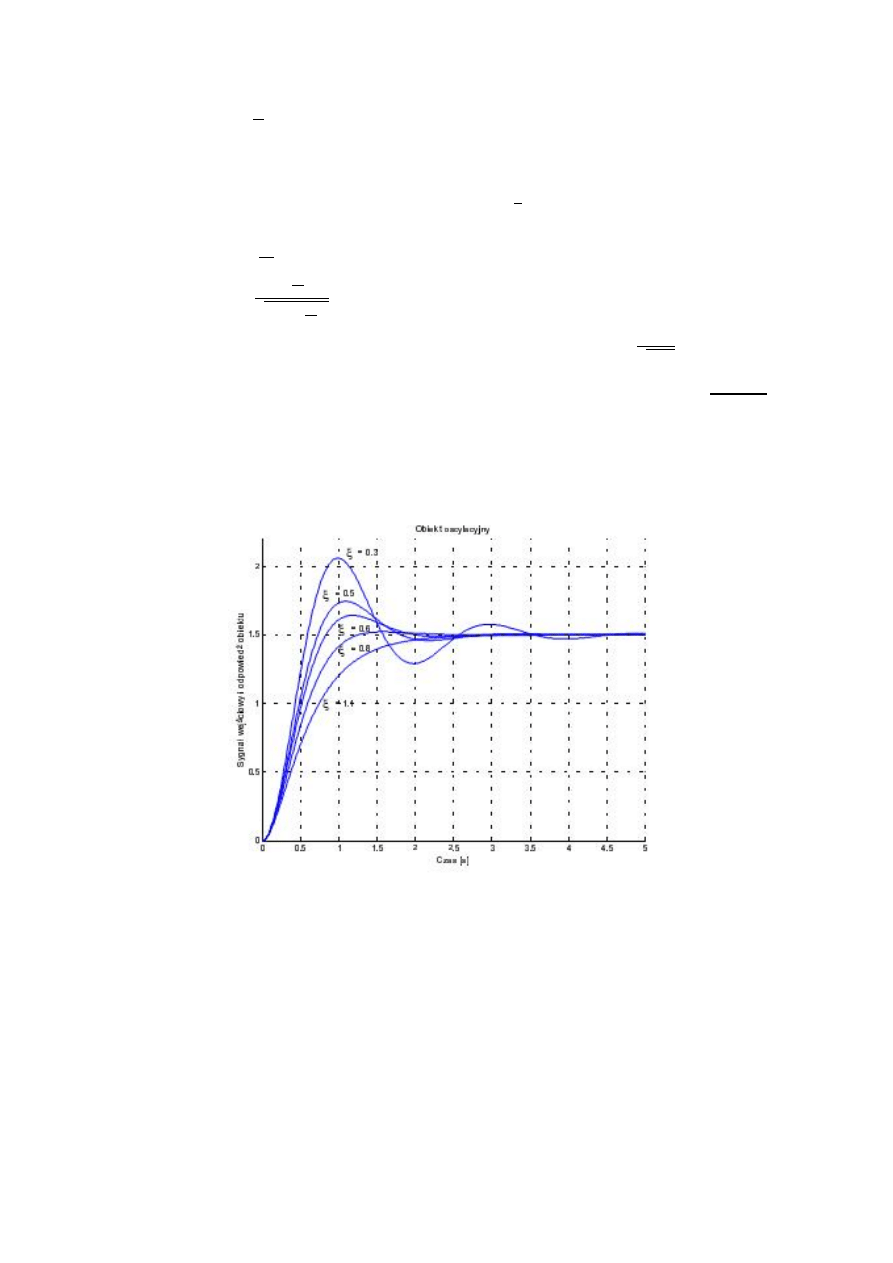
Rys. 10. Odpowiedź obiektu oscylacyjnego na skok jednostkowy 1(t).
Wzór (35) można zapisać w nieco odmiennej postaci:
( ) =
1 −
sin
1 −
+
(36)
11
przy czym =
.
Kroki obliczania parametrów obiektu oscylacyjnego:
1) Z wykresu odpowiedzi obiektu znajduje się wartość oraz amplitudy pierwszych ekstremów
,
.
2) Ze wzoru
=
wylicza się częstotliwość .
3) Ze wzoru =
można wyliczyć współczynnik tłumienia.
4) Mając policzone wartości i można, na podstawie wzoru =
, obliczyć stałą
tłumienia .
5) Częstotliwość drgań własnych nietłumionych można obliczyć ze wzoru
= √
+
, a
stąd stałą czasową .
Poniżej zostanie przedstawiony wpływ współczynnika tłumienia na zmianę kształtu odpowiedzi
obiektu oscylacyjnego na skok jednostkowy 1( ).
Rys. 11. Odpowiedź obiektu na skok jednostkowy 1(t) przy różnych wartościach tłumienia ξ.
W przypadku granicznym, gdy = 0, co odpowiada założeniu, że w układzie nie ma rozpraszania
energii, równanie (32) redukuje się do postaci:
̈ ( ) + ( ) =
( ) .
(37)
Oscylacje jakie wtedy powstają na wyjściu układu, są niegasnące – o stałej amplitudzie.
Dla przypadku, gdy ≥ 1, odpowiedź na skok jednostkowy 1( ) ma charakter aperiodyczny. Obiekt
przestaje być oscylacyjny a przechodzi w inercyjny II-rzędu, który został wcześniej omówiony.
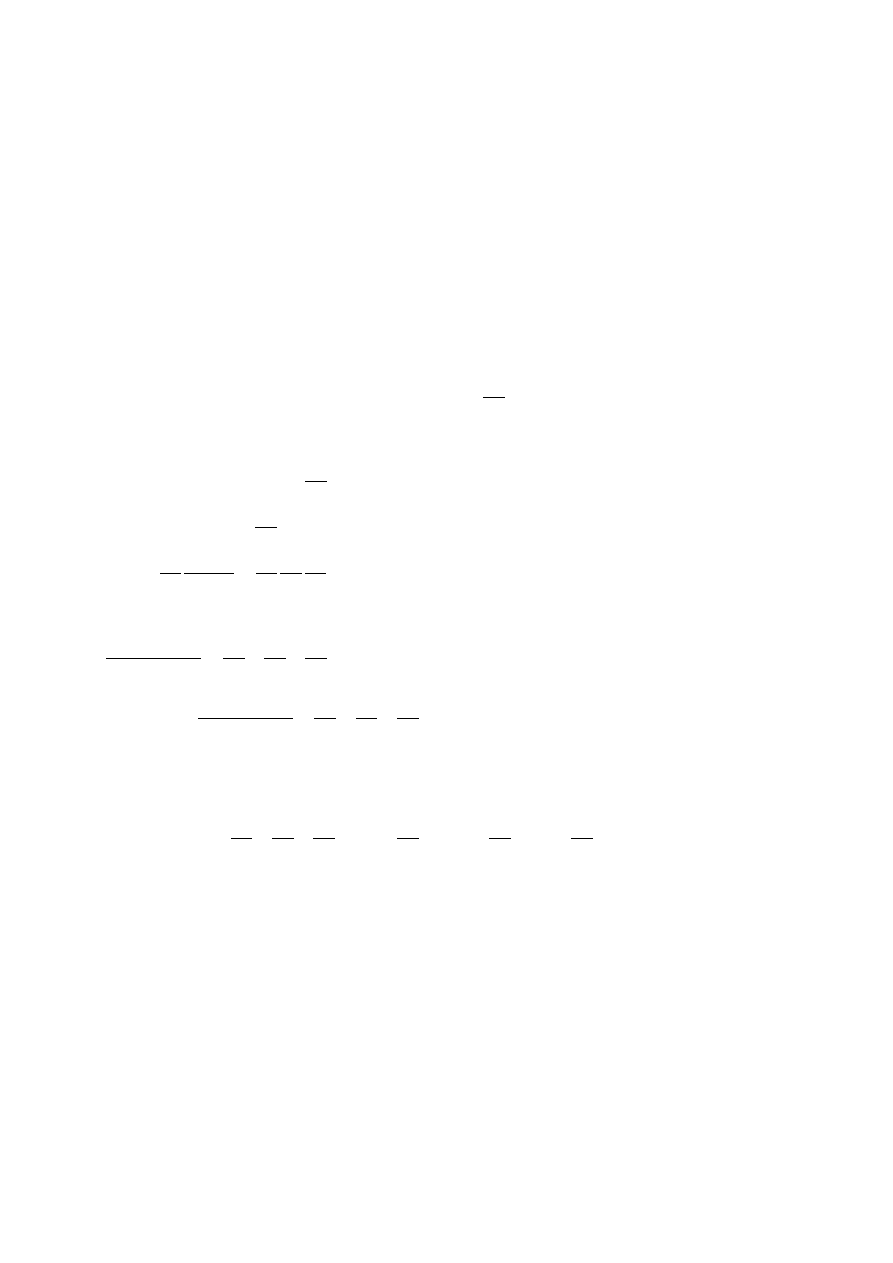
12
3. Rozwiązywanie równań różniczkowych metodą operatorową
Należy rozwiązać równanie różniczkowe:
̈( ) − 3 ̇( ) + 2 ( ) = 2
,
(38)
z następującymi warunkami początkowymi:
(0) = ̇(0) = 0 .
(39)
Proces obliczania rozpoczyna się od policzenia transformaty Laplace’a dla równania (38):
{ ̈( ) − 3 ̇( ) + 2 ( )} = {2
} ,
(40)
( ) −
(0) − ̇(0) − 3
( ) − (0) + 2 ( ) =
.
(41)
Podstawiając następnie wartości początkowe ze wzoru (39) do wzoru (41) otrzymujemy:
( ) − 3
( ) + 2 ( ) =
,
( )(
− 3 + 2) =
,
(42)
( ) =
=
.
Teraz należy rozbić równanie na czynniki pierwsze:
(
)(
)(
)
=
+
+
⇒
= 1
= −2
= 1
⇒
(
)(
)(
)
=
−
+
.
(43)
Teraz stosując odwrotną transformatę Laplace’a otrzymuje się rozwiązanie równania
różniczkowego (38) z warunkami początkowymi (39):
{ ( )} =
−
+
=
− 2
+
,
(44)
( ) =
− 2
+
.
Zadania do samodzielnego rozwiązania:
̈( ) + 2 ( ) = 2 cos ,
(0) = 0, ̇(0) = −1,
(45)
̈( ) + 2 ̇( ) + 2 ( ) = 8
,
(0) = −4, ̇(0) = 2,
(46)
̈( ) + 4 ̇( ) + 2 ( ) =
,
(0) = 1, ̇(0) = 2,
(47)
̈( ) − 6 ̇( ) + 9 ( ) =
,
(0) = 2, ̇(0) = 6,
(48)
̈( ) + 4 ̇( ) + 6 ( ) = 1 +
,
(0) = ̇(0) = 0,
(49)
13
4. Zestawienie podstawowych własności transformaty Laplace’a
4.1. Addytywność
{ ( ) +
( )} =
( ) +
( )
(50)
4.2. Mnożenie przez stałą
{
( )} =
( )
(51)
przy czym jest liczbą rzeczywistą.
4.3. Różniczkowanie względem czasu
{
( )} =
( ) −
(0) −
( )
(0) − ⋯ −
(
)
(0)
(52)
4.4. Całkowanie względem czasu
∫
( )
=
( )
(53)
4.5. Przesunięcie względem czasu na płaszczyźnie rzeczywistej
{ ( − )} =
( ) ≥ 0
(54)
4.6. Przesunięcie względem s na płaszczyźnie zmiennej zespolonej
{
( )} = ( + )
(55)
przy czym jest liczbą zespoloną.
4.7. Zmiana skali czasu
=
(
)
(56)
przy czym jest liczbą rzeczywistą różną od zera.
4.8. Splot funkcji czasu
∫
( − ) ( )
=
( ) ∗
( )
(57)
4.9. Twierdzenie o wartości początkowej
(0) = lim
→
( ) = lim
→
( )
(58)
Powyższe twierdzenie jest prawdziwe, gdy obie granice istnieją.
14
4.10. Twierdzenie o wartości końcowej
(∞) = lim
→
( ) = lim
→
( )
(59)
Powyższe twierdzenie jest prawdziwe, gdy obie granice istnieją.
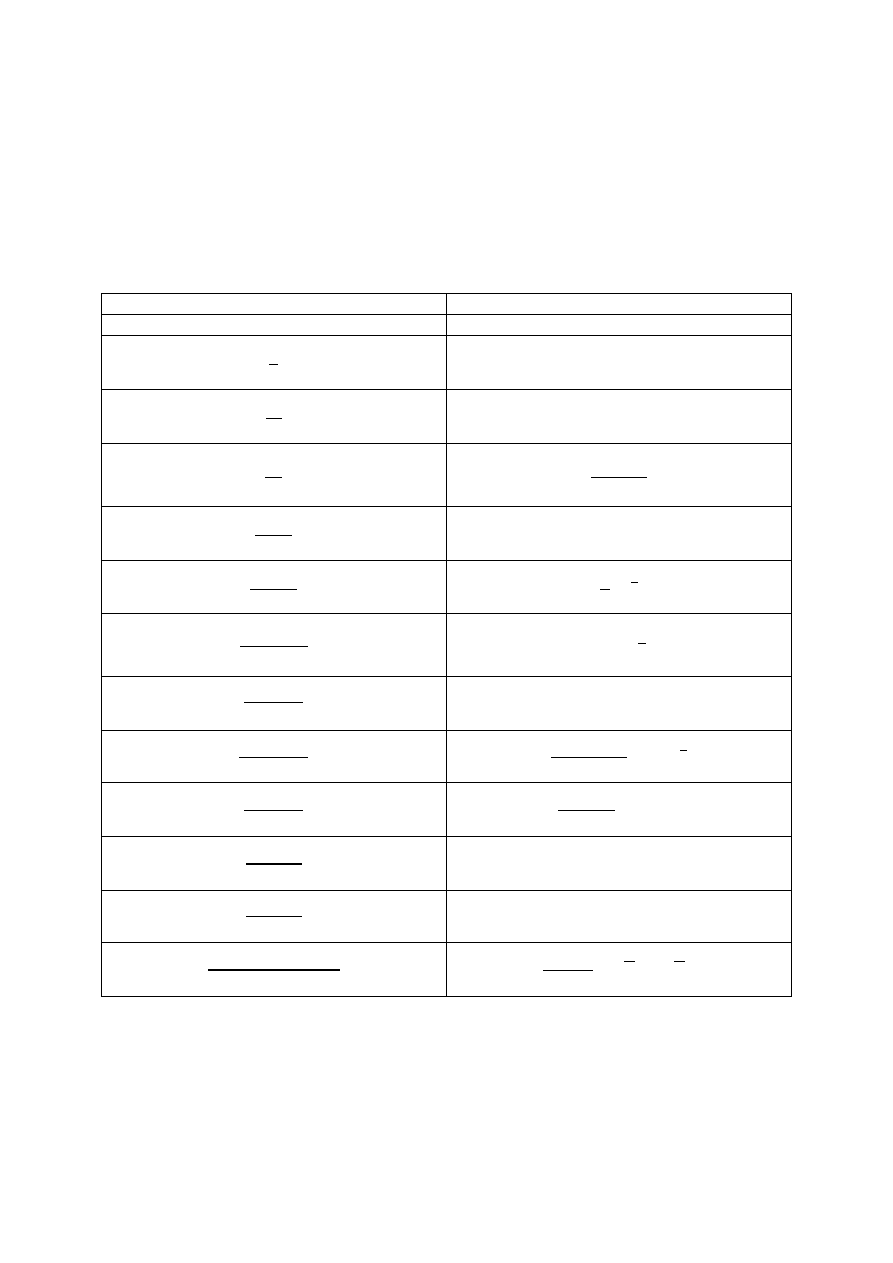
5. Zestawienie podstawowych transformat Laplace’a
F(s)
f(t)
1
impuls jednostkowy δ(t)
1
1( )
1
1
( − 1)!
1
+
1
+ 1
1
1
(
+ 1)
1 −
( + )
1 −
1
(
+ 1)
1
( − 1)!
1
( + )
1
( − 1)!
+
cos
+
sin
1
(1 +
)(1 +
)
1
−
−
15
6. Podłączenie stanowiska i sposób pomiaru
6.1. Schemat połączeń elektrycznych
Rys. 12. Schemat połączenia generator – obiekt - oscyloskop.
Na rys. 12 został przedstawiony schemat, według którego należy połączyć generator, obiekt
i oscyloskop celem przeprowadzenia ćwiczenia. Generator kształtuje sygnał zadany (w przypadku
badania układu na skok jednostkowy 1( ) jest to sygnał prostokątny). Sygnał z generatora podawany
jest na obiekt i na jedno z wejść oscyloskopu. Na drugie wejście oscyloskopu podawany jest sygnał
wyjściowy z obiektu.
6.2. Schemat połączeń elektrycznych
Po podłączeniu wszystkich obiektów należy odpowiednio ustawi na oscyloskopie podstawę
czasu i podziałkę napięcia, tak aby oba sygnały, z generatora i z obiektu, były pokazywane
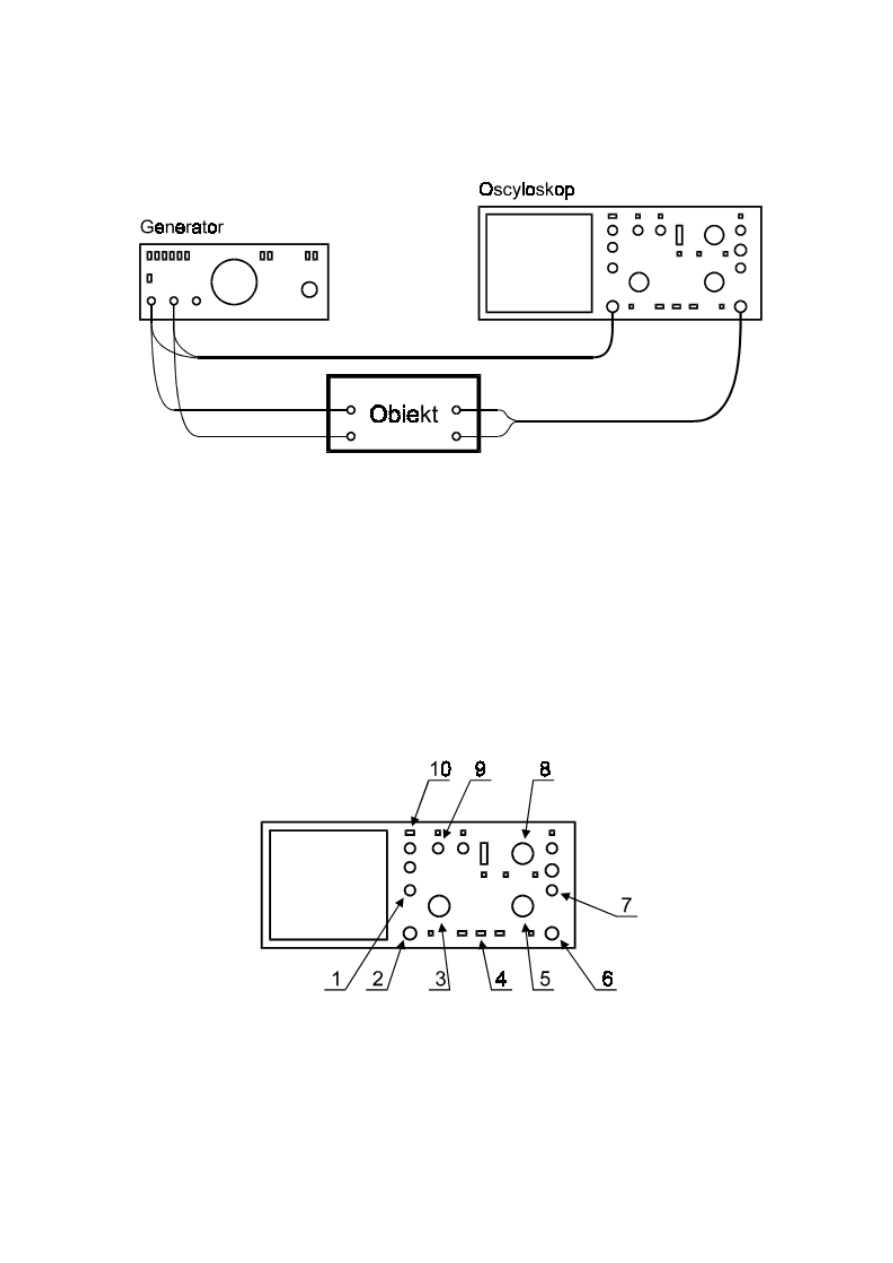
jednocześnie. Przy ustawianiu oscyloskopu może okazać się pomocny rys. 13.
Rys. 13. Oscyloskop.
Na rys. 13 został przedstawiony oscyloskop. Za pomocą przycisku (10) można załączyć
oscyloskop. Sygnały wejściowe podaje się na wejście 1 (2) lub na wejście 2 (6). Wykresy sygnałów
wejściowych można przesunąć w pionie za pomocą potencjometru (1) – dla kanału 1 lub
potencjometru (7) – dla kanału 2. Podziałkę napięciową ustawia się dla kanału 1 za pomocą
16
przełącznika (3), a dla kanału 2 za pomocą przełącznika (5). Podstawę czasu, która jest taka sama dla
obu kanałów, ustawia się za pomocą przełącznika (8). Do przesunięcia wykresów w osi OX służy
potencjometr (9).
6.3. Przebieg ćwiczenia
Należy wykonać pomiaru sześciu członów dynamicznych (proporcjonalny, inercyjny I-rzędu,
różniczkujący z inercją I-rzędu, całkujący z inercją I-rzędu, inercyjny II-rzędu, oscylacyjny). Wyniki
pomiarów w postaci oscylogramów zarejestrować aparatem fotograficznym. Następnie należy
zbudować w/w człony, przy użyciu bloków podanych przez prowadzącego, w programie Simulink,
a otrzymane wyniki symulacji zachować do późniejszej obróbki.
6.4. Sprawozdanie
Do wykonania sprawozdania będą niezbędne parametry elementów, z których wykonane
są badane człony dynamiczne. Wartości tych parametrów zostaną podane przez prowadzącego
na końcu zajęć. Sprawozdanie z ćwiczenia ma zawierać:
1) Obliczenia parametrów ( , ,
) w oparciu o podane wartości elementów.
2) Krótki opis członów dynamicznych (np. poprzez zamieszczenie ich schematów z Simulinka,
równania różniczkowe opisujące te człony, transmitancje) oraz opis oscylogramów poprzez
wyznaczenie na nich charakterystycznych wartości tak, jak to pokazano na przykładowych
charakterystykach w części teoretycznej niniejszej instrukcji do zajęć.
3) Porównanie oscylogramów z charakterystykami uzyskanymi w symulacjach. Należy pamiętać
o użyciu takich samych parametrów w symulacji ( , ,
,
.).
4) Przykłady zastosowania członów dynamicznych w życiu codziennym i/lub technice. Należy
zaznaczyć co jest wymuszeniem ( ( )), a co jest odpowiedzią ( ( )).
5) Wnioski i obserwacje nasuwające się po przeprowadzonych badaniach.