1

Algorytmy i
struktury
danych

Wykład 4

2

1. Sortowanie Shella (ang.
shellsort)



Sortowanie polegające na podzieleniu
tablicy na kilka podtablic.



Dokonujemy tego wybierając liczby
przeskakując po tablicy (pierwotnej) co
h pozycji. Każdą z tych h podtablic
sortujemy, zmniejszamy h i znów
sortujemy kolejne (większe) podtablice.
Operację tą wykonujemy aż będziemy
mieli jedną tablicę do posortowania.

3

Sortowanie podtablic



Do posortowania podtablic wykorzystujemy

algorytm sortowania przez wstawianie, lub

sortowanie bąbelkowe.



Wynika to z faktu, że co krok algorytmu

nasza tablica będzie „coraz bardziej

posortowana”, a algorytmy te są tym

bardziej efektywne, im bardziej jest

„posortowana” tablica wejściowa.



Nie wolno wykorzystywać sortowania przez

wybór, gdyż wtedy złożoność sortowania

wzrośnie do O(n

2

).

4

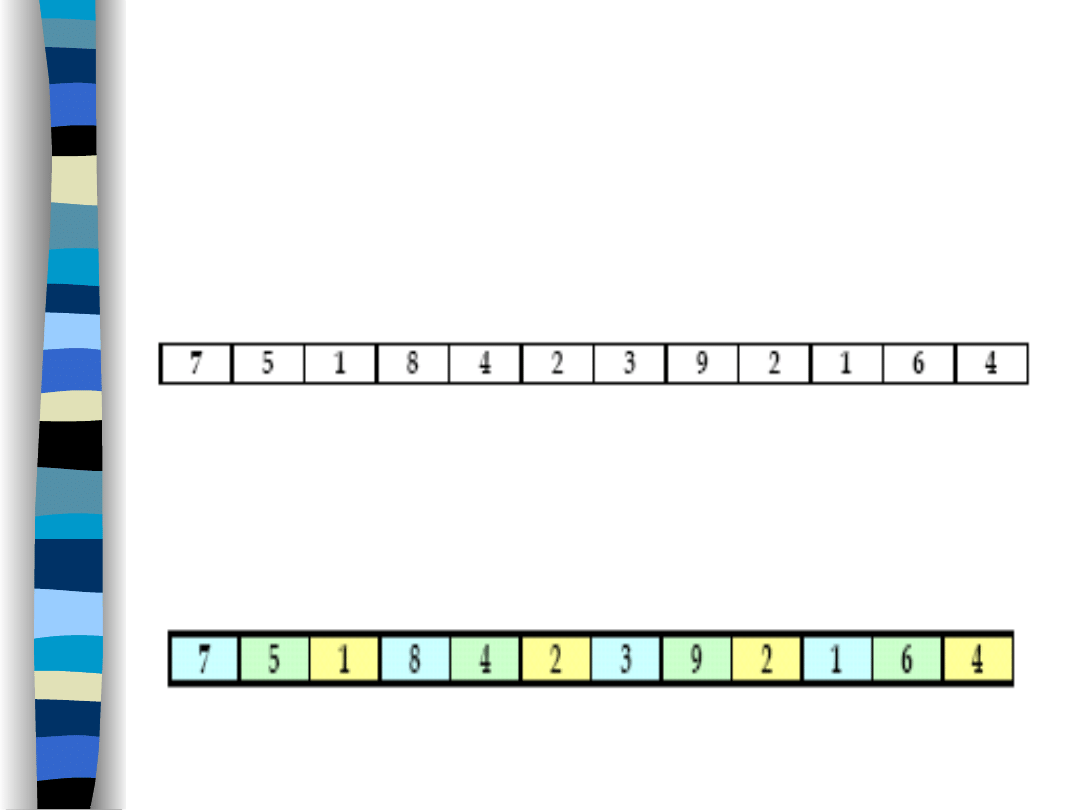
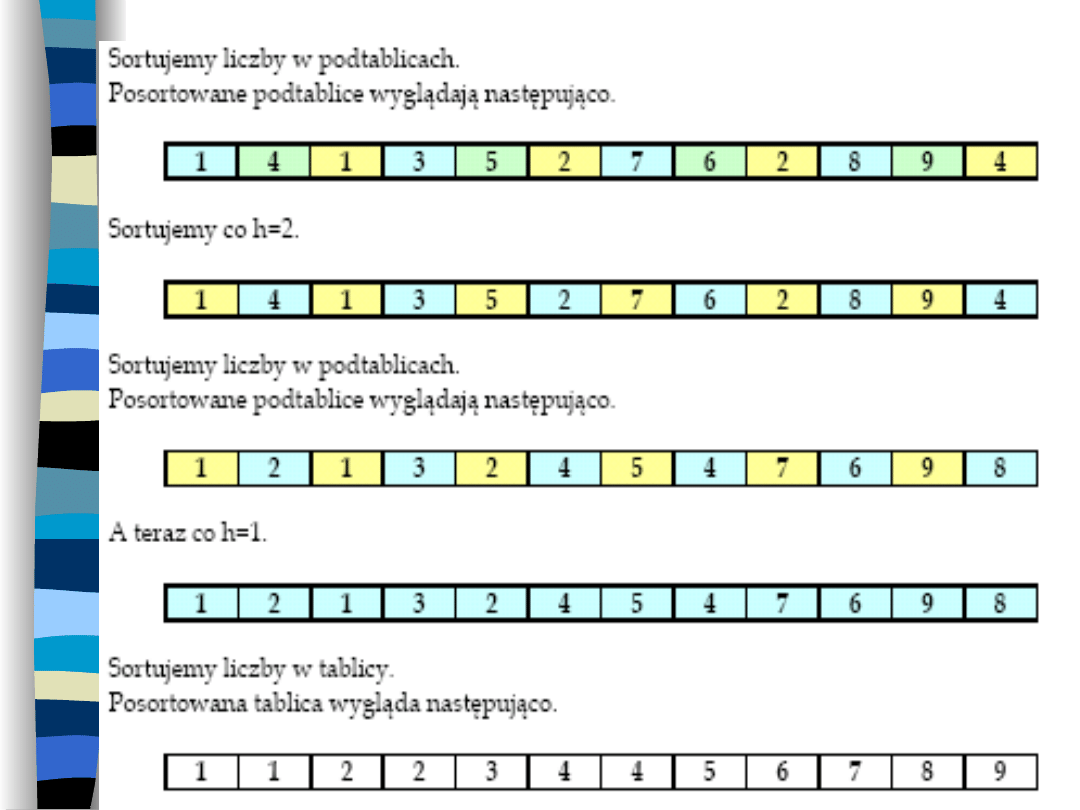
Przykład sortowania
Shella

Ustalamy, że sortujemy co 3 (h=3).
Podzielone podtablice zaznaczamy na
rożne kolory.

Tablica do posortowania:

5

6

Złożoność sortowania
Shella



Stwierdzono, że jeżeli pierwszy krok
będzie sortował co (16n/π)

1/3

, a drugi co 1

to złożoność takiego algorytmu będzie
wynosić O(n

5/3

).



Aby uzyskać złożoność O(n

5/4

) kroki

należy dobierać wg tzw. zasady Knutha.



Złożoność tego algorytmu jest lepsza od
O(n

2

), ale ciągle brakuje jej do

osiągnięcia złożoności O(n ln n).

7

Zasada Knutha



Ostatni krok jest zawsze równy 1, a każdy poprzedni

powstaje z pomnożenia go przez 3 i dodania 1.

Dodatkowo należy dobrać pierwszy (h

k

) krok tak, że

krok h

k

+2 byłby większy lub równy liczbie n (ilość

elementów w tablicy).

 h

1

=1

 h

i

=3h

i-1

+1

 h

k

(początkowe) musi być tak dobrane, aby h

k

+2 ≥

n, gdzie n to ilość liczb do posortowania.



Wartości h

i

będą więc wynosić: 1, 4, 13, 40, 121, 364,

1093,…



Należy zauważyć, że minimalna ilość liczb musi być

równa przynajmniej 13. Dla mniejszej tablicy stosujemy

sortowanie przez wstawianie od razu dla całej tablicy.

8

Przykład stosowania
zasady Knutha



Mamy n=1000 liczb.



Wartości h

i

będą wynosić:

1,4,13,40,121,364,1093,…



Wartość pierwszego kroku
dobieramy zgodnie z podanym
warunkiem, a więc będzie to h

5

=121

ponieważ h

7

jest już większe od 1000

(1093).

9

2. Sortowanie przez
kopcowanie (ang.
heapsort)



Do tego algorytmu
wykorzystywany jest kopiec.



Algorytm ten ma złożoność rzędu
O(n ln n).

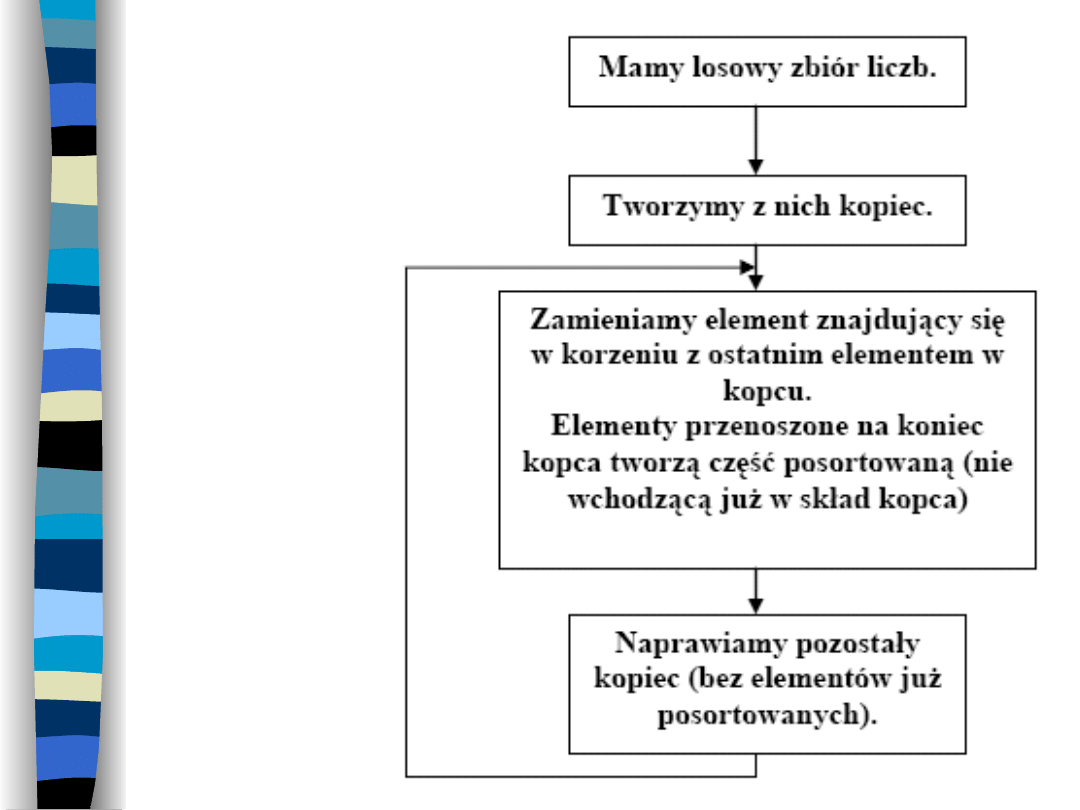
10

Algorytm
sortowani
a przez
kopcowan
ie

11

3. Sortowanie szybkie
(ang. quicksort)



Dzielimy daną tablicę liczb na dwie
podtablice, gdzie każdy element
pierwszej podtablicy będzie nie
większy od każdego elementu
drugiej.



To samo robimy z każdą podtablicą
z osobna (rekurencyjnie) aż
uzyskamy tablice jednoelementowe.

12



W celu podziału tablicy wybieramy element wg

którego będziemy dokonywać podziału.



Można wybrać pierwszy element tablicy (tak jak

w poniższym przykładzie), ale można również

wybrać losowo element z tablicy. Drugi wariant

zabezpiecza nas przed sytuacją, w której nasza

tablica do posortowania będzie prawie

uporządkowana (co spowoduje niekorzystne

mało równomierne podziały). Wtedy wybranie

losowego elementu spowoduje w miarę

równomierny podział na podtablice.



Dzięki losowemu składnikowi nie stracimy na

efektywności algorytmu.

13



Do podziału na podtablice można wykorzystać dwa

wskaźniki: np. niebieski i czerwony.



Pierwszy (niebieski ) przesuwamy w lewo dopóty,

dopóki wskazuje na element większy lub równy

elementowi dzielącemu.



Czerwony wskaźnik przesuwamy w prawo aż nie

napotka na element większy lub równy elementowi

dzielącemu.



Dopóki wskaźniki się nie minęły to zamieniamy

miejscami elementy na które wskazują wskaźniki i

przesuwamy je dalej. Jeśli się miną to tablica zostanie

podzielona na dwie części. Dla każdej podtablicy

wykonujemy to samo.

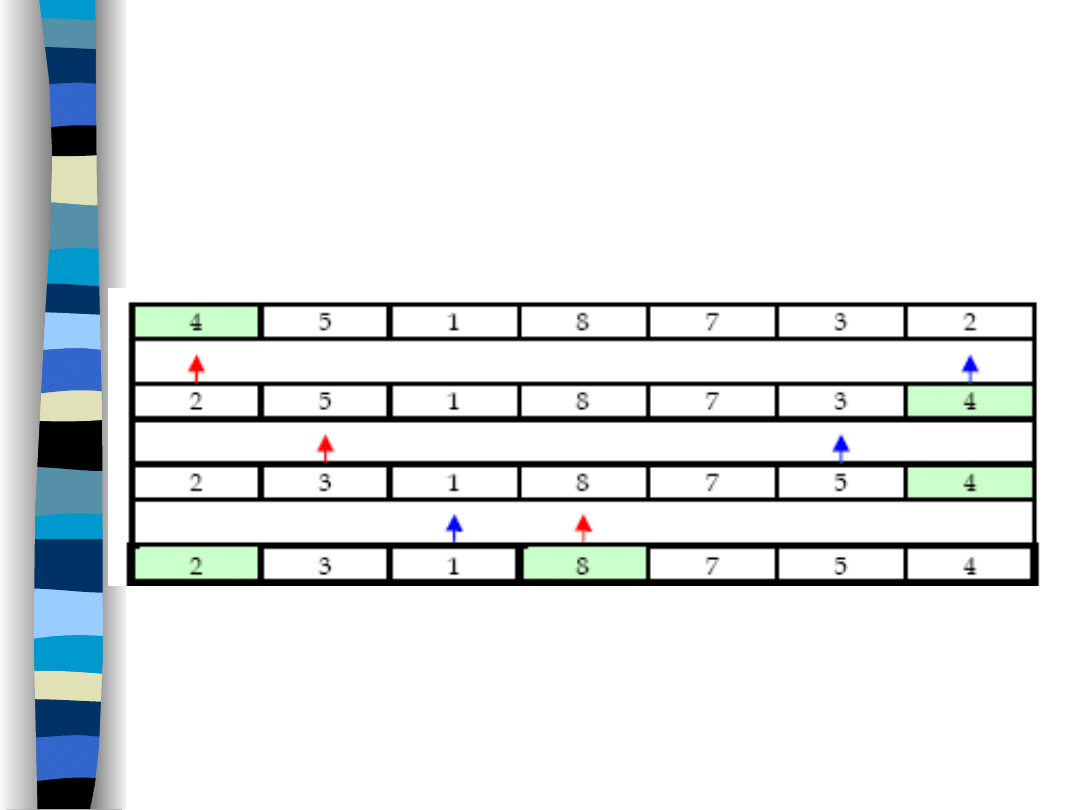
14

Przykład: pierwszy podział
na 2 podtablice.

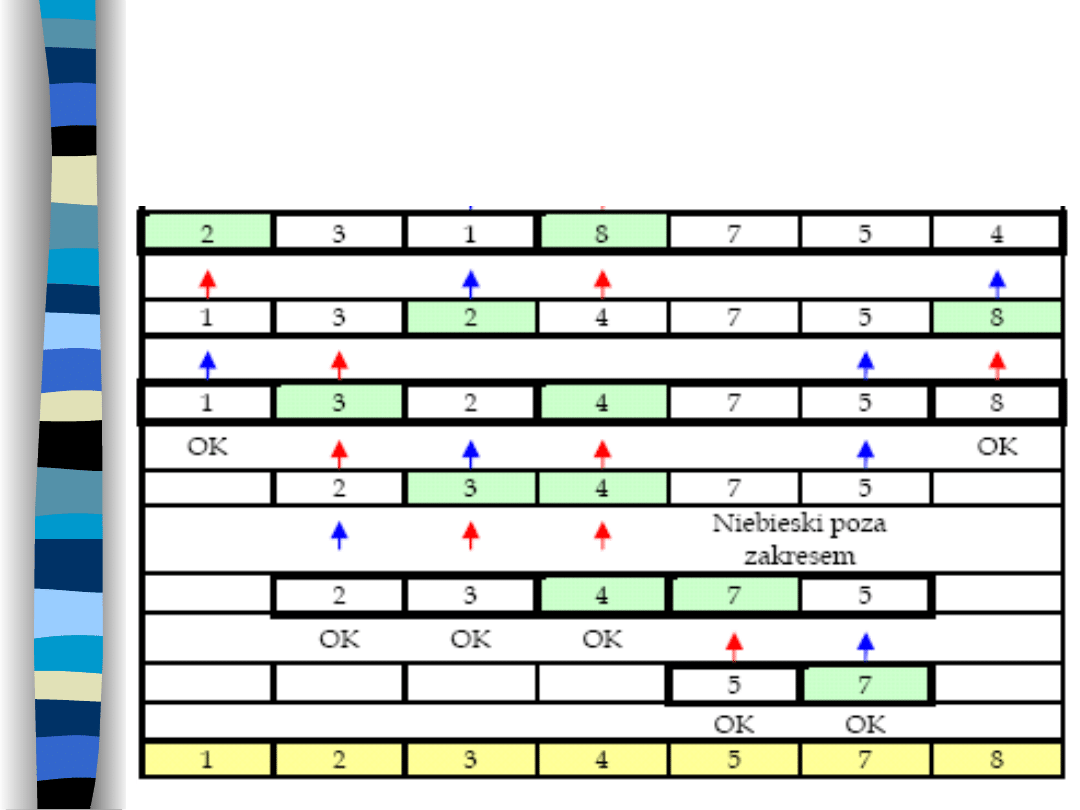
15

Cd.
przykładu:Rekurencyjny
podział podtablic

16

Złożoność algorytmu



W sytuacji pesymistycznej, gdy w każdym

przypadku jako element dzielący wybierzemy

element najmniejszy (lub największy) z

tablicy. Podział będzie wtedy zawsze na

pojedynczy element oraz resztę tablicy. Wtedy

złożoność algorytmu quicksort wyniesie O(n

2

).



Wariant optymistyczny zakłada, że każda

podtablica podzieli się zawsze dokładnie na

pół.



W sytuacji pośredniej oczekiwana złożoność

algorytmu wynosi O(n ln n).

17

4. Sortowanie przez
scalanie (ang. mergesort)



Sortowanie wykorzystujące rekurencję.



Złożoność tego algorytmu wynosi O(n
ln n).



Dzielimy tablicę z liczbami na 2
podtablice. Te podtablice znów
dzielimy na dwie. Czynność tą
wykonujemy do uzyskania tablic
jednoelementowych.

18



Innymi słowy wykorzystujemy metodę
dziel i rządź - dzielimy problem,
którego nie potrafimy rozwiązać na
mniejsze.



Te małe problemy są już tak proste, że
ich rozwiązanie nie sprawia nam
problemów. Po podzieleniu tablicy
scalamy te podtablice jednocześnie
sortując.

19



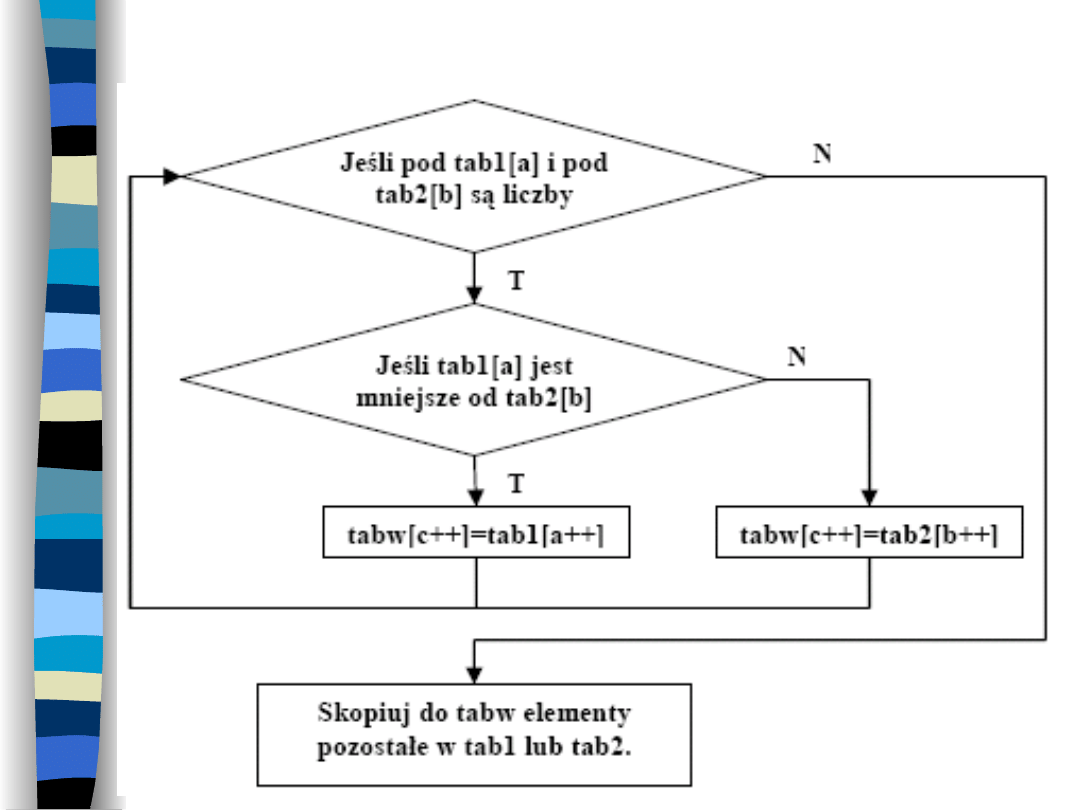
Sortowanie odbywa się poprzez
zastosowanie pewnego schematu
scalania tablic.



Mamy dwie podtablice: pierwsza ma 0-n
elementów i jest indeksowana zmienną
a, druga ma 0-m elementów i jest
indeksowana zmienną b oraz tablice
wynikową (scaloną) o n+m elementach
– indeksowaną zmienną c.

20

21

Algorytmy
rekurencyjne

22

Metoda dziel i rządź



Czasami problem można rozłożyć na

coraz to prostsze, których rozwiązanie

nie wymaga wysiłku lub wymaga bardzo

małego wysiłku. Rozwiązujemy te proste

problemy wracając do coraz

trudniejszych, aż okaże się, że główny

(wyjściowy) problem został rozwiązany.

Nazywa się to metodą dziel i rządź.



Metoda ta często okazuje się bardzo

skuteczna, a niekiedy nawet jedyna.



Rekurencję bardzo wygodnie się implementuje,

stosujemy po prostu wywołania podprogramów,

a maszyna cyfrowa liczy za nas.

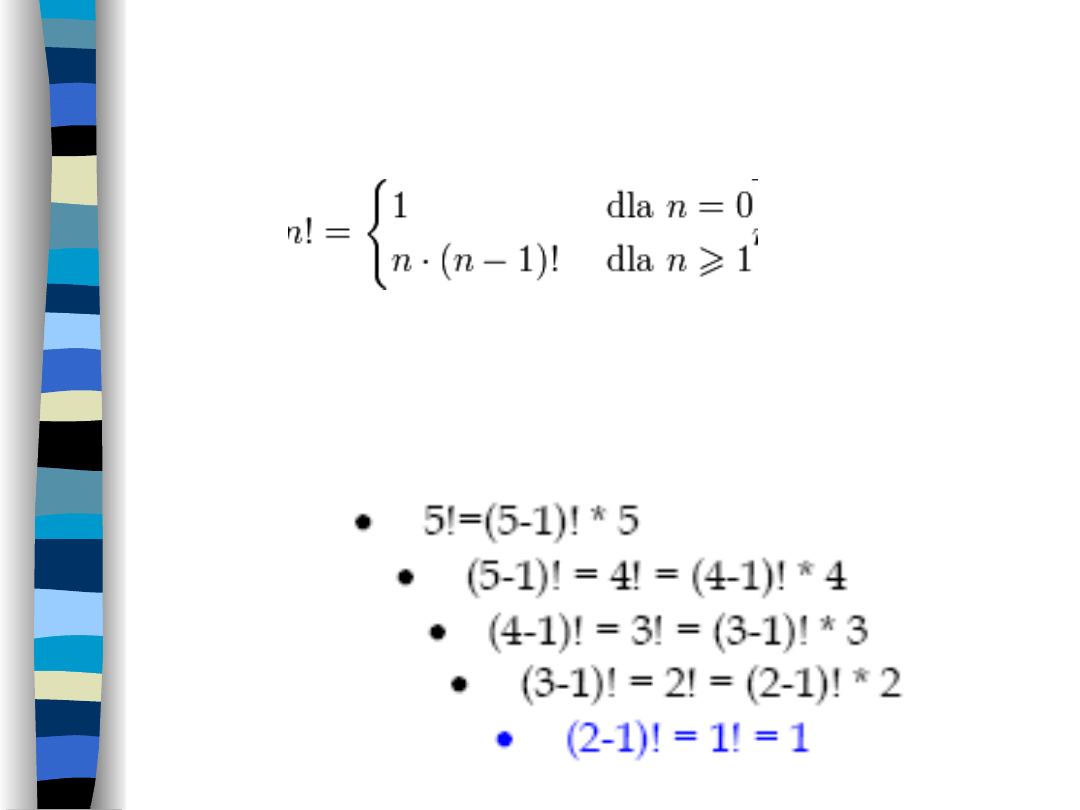
23

1 Silnia (liczona
rekurencyjnie)



Przykład: mamy obliczyć 5!. Korzystamy
ze wzoru, bo wiemy, że 5! to 4!
mnożone przez 5. Podobnie dalej.

24



Rozkładamy(zagłębiamy się w rekurencji) tak

długo, aż dojdziemy do problemu, który

potrafimy rozwiązać (

na niebiesko

): 1! - która

z definicji wynosi 1.



Następnie wracamy z powrotem. Wiedząc ile

wynosi 1! umiemy obliczyć 2!.



Wiedząc ile wynosi 2! Umiemy obliczyć 3! itd.

W ten sposób udało się obliczyć silnie z 5.



Czyli: wykorzystaliśmy rekurencję do

rozłożenia problemu na szereg mniejszych,

czyli zastosowaliśmy metodę dziel i rządź.

25

2. NWD – największy
wspólny dzielnik
(algorytm Euklidesa)

Wzory:

NWD(x,y) = NWD(y,x % y) dla x>y
NWD(y,x) = NWD(x,y % x) dla y>x

gdzie % oznacza dzielenie modulo.

Rozkładamy problem na mniejsze według tego

wzoru do mementu, aż gdy drugi z

argumentów osiągnie wartość zero.

26

Przykład algorytmu
Euklidesa



Mamy obliczyć NWD dla 26 i 8.

Obliczamy NWD dla 8 i (26%8)=2
Obliczamy NWD dla

2

i (8%2)=

0



Gdy druga z liczb będzie równa
zero to pierwsza jest NWD. Zatem
NWD dla 26 i 8 wynosi 2.

27

3. Wypisywanie wyrazu
od końca



Aby rozwiązać to zadanie
rozbijamy je na dwa kroki:

1. próbujemy wypisać w odwrotnej

kolejności wszystko z wyjątkiem
pierwszego znaku (wywołujemy
rekurencyjnie nasz podprogram)

2. wypisujemy pierwszy znak

wyrażenia.

28

Przykład: słowo „notatka”

29

Przykładowe zastosowanie: chcemy

wypisać od końca zawartość naszej
listy jednokierunkowej (np.
posortowanej rosnąco, gdy my
potrzebujemy posortowanej
malejąco).

30

Algorytmy zachłanne
(ang. greek algorithm
(sic!))



Algorytmy te nie przewidują tego,
co będzie „potem”. Interesuje ich
tylko „teraz”.



Innymi słowy postępują zachłannie.
Takie działanie nie zawsze okazuje
się najlepsze, ale bywa że jest
idealne.

31

Problem kasjera



Mając następujący system monetarny: 1, 2,
5, 10, 20, 50 wydajemy resztę w taki
sposób, aby stracić jak najmniej monet.
Postępując zgodnie z zasadami algorytmu
zachłannego za każdym razem będziemy
wydawać monety o największym nominale.



Doprowadzi nas to w tym wypadku do
optymalnego rozwiązania – wydamy
najmniejszą ilość monet.

32

Przykład: Wydać 79
złotych.



wydajemy 50, zostaje 29zł



wydajemy 20, zostaje 9zł



wydajemy 10, zostaje 9zł



wydajemy 5, zostaje 4zł



wydajemy 2, zostaje 2zł



wydajemy 2, zostaje 0zł



Stosując powyższą metodę wydaliśmy 6

monet i lepiej się nie da.

33



Ale - rzecz jasna - nie dla każdej
sytuacji algorytmy zachłanne dają
optymalne rozwiązanie.



Przykład: system monetarny: 1,10,
20, 25.

34

Kontrprzykład przeciw
zachłanności



Przykład: Mając system: 1, 10, 20, 25. Wydać 31

złotych.

– wydajemy 25, zostaje 6zł
– wydajemy 1, zostaje 5zł
– wydajemy 1, zostaje 4zł
– wydajemy 1, zostaje 3zł
– wydajemy 1, zostaje 2zł
– wydajemy 1, zostaje 1zł
– wydajemy 1, zostaje 0zł



Wydaliśmy 7 monet, co nie jest minimalną liczbą

monet. Można było wydać 20 + 10 + 1 co daje

tylko trzy monety. W tym przypadku algorytm

zachłanny nie zadziałał optymalnie.