Wykład 13

MECHANIKA TEORETYCZNA

Studia stacjonarne I stopnia – rok akademicki 2013/14

Autor:

Henryk Laskowski

Katedra Podstaw Mechaniki Ośrodków Ciągłych
Instytut Mechaniki Budowli
Wydział Inżynierii Lądowej

Dynamika punktu materialnego

Część 1

Wprowadzenie

3

1.1. Ogólna klasyfikacja

MECHANIKA – dział fizyki poświęcony badaniu ruchów i stanów

równowagi ciał. Obejmuje statykę, kinematykę
i dynamikę

Kinematyka – dział mechaniki zajmujący się opisem ruchu

ciał bez uwzględnienia jego przyczyn oraz
cech fizycznych ciał.

Dynamika

– dział mechaniki badający ruch ciał
materialnych pod wpływem działających
na nie sił

Kinematyka – dział mechaniki zajmujący się opisem ruchu

ciał bez uwzględnienia jego przyczyn oraz
cech fizycznych ciał.

Statyka

– dział mechaniki badający prawa równowagi

ciał będących pod działaniem sił

Statyka

– dział mechaniki badający prawa równowagi

ciał będących pod działaniem sił

4

1.2. Założenia

Dynamika bazuje na aksjomatach mechaniki, które zostały
sformułowane na podstawie obserwacji zjawisk przyrodniczych:

1. aksjomat bezwładności

2. aksjomat ruchu

3. aksjomat akcji-reakcji

Siła, masa, czas - są pojęciami pierwotnymi

Masa punktu materialnego jest niezmienna w czasie ruchu

Siła w ogólnym przypadku może być funkcją czasu, położenia i

prędkości

5

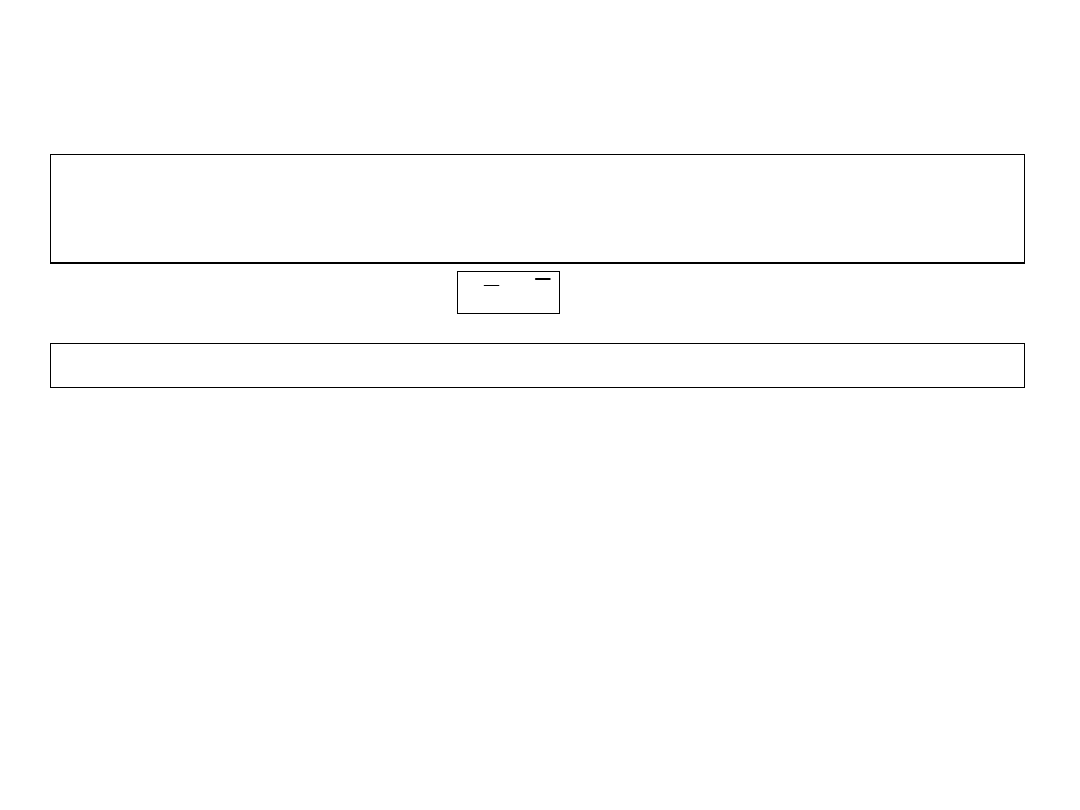
Prawo ruchu punktu materialnego można zapisać na

podstawie II zasady

dynamiki w postaci wektorowej:

mr F

=

&&

1.3. Równania ruchu punktu materialnego poddanego działaniu siły

Można je sprowadzić do trzech równań skalarnych:

(

)

(

)

(

)

x

y

z

mx F x,y,z,x,y,z,t
my F x,y,z,x,y,z,t
mz F x,y,z,x,y,z,t

=

=

=

&&

&&&

&&

&&&

&&

&&

&

( )

(

)

( )

(

)

( )

(

)

x

y

z

x

f x,y,z,x,y,z,t

y

f x,y,z,x,y,z,t

z

f x,y,z,x,y,z,t

=

=

=

g

g

g

&

&&&

&

&&&

&&

&

&

6

( )

(

)

( )

(

)

( )

(

)

x

y

z

x

f x,y,z,x,y,z,t

y

f x,y,z,x,y,z,t

z

f x,y,z,x,y,z,t

=

=

=

g

g

g

&

&&&

&

&&&

&&

&

&

(

)

(

)

(

)

x

x

y

y

z

z

φ x,y,z,x,y,z,t

C

φ x,y,z,x,y,z,t

C

φ x,y,z,x,y,z,t

C

=

=

=

&&&

&&&

&&&

Wyznaczenie całek pierwszych równań ruchu

(

)

(

)

(

)

x

x

y

z

y

x

y

z

z

x

y

z

xν x,y,z,C ,C ,C ,t

yν x,y,z,C ,C ,C ,t

zν x,y,z,C ,C ,C ,t

=

=

=

&

&

&

(

)

(

)

(

)

x

x

y

z

x

y

x

y

z

y

z

x

y

z

z

ψ x,y,z,C ,C ,C ,t

D

ψ x,y,z,C ,C ,C ,t

D

ψ x,y,z,C ,C ,C ,t

D

=

=

=

Wyznaczenie całek drugich równań ruchu

7

(

)

(

)

(

)

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

x x C ,C ,C ,D ,D ,D ,t

y y C ,C ,C ,D ,D ,D ,t

z z C ,C ,C ,D ,D ,D ,t

=

=

=

(

)

(

)

(

)

(

)

(

)

(

)

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

x

y

z

x

y

z

x

y

z

x

x

y

z

x

y

z

x

y

z

y

x

y

z

x

y

z

x

y

z

z

x C ,C ,C ,D ,D ,D ,t

x ,

x x ,y ,z ,C ,C ,C ,t

v

y C ,C ,C ,D ,D ,D ,t

y ,

y x ,y ,z ,C ,C ,C ,t

v

z C ,C ,C ,D ,D ,D ,t

z ,

z x ,y ,z ,C ,C ,C ,t

v

=

=

=

=

=

=

&

&

&

x

y

z

x

y

z

ˆ ˆ ˆ

C , C , C

ˆ ˆ

ˆ

D , D , D

- rozwiązanie ogólne równań ruchu

Warunki początkowe (lub brzegowe)

(

)

(

)

(

)

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

x

y

z

ˆ ˆ ˆ ˆ ˆ ˆ

x x C ,C ,C ,D ,D ,D ,t

ˆ ˆ ˆ ˆ ˆ ˆ

y y C ,C ,C ,D ,D ,D ,t

ˆ ˆ ˆ ˆ ˆ ˆ

z z C ,C ,C ,D ,D ,D ,t

=

=

=

- rozwiązanie szczególne równań ruchu

Całki drugie po przekształceniach

8

1.4. Stopnie dynamicznej swobody

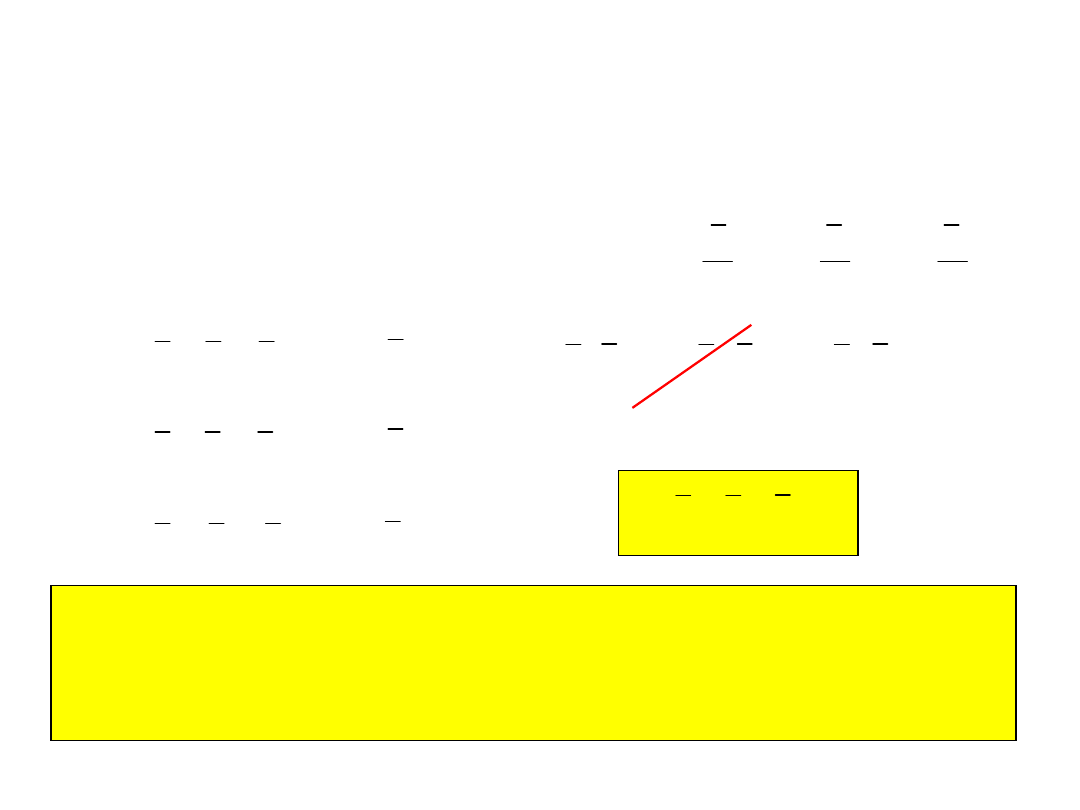
Liczba stopni swobody – liczba niezależnych parametrów opisujących
położenie lub konfigurację układu materialnego.

Przykłady z zakresu statyki bryły sztywnej

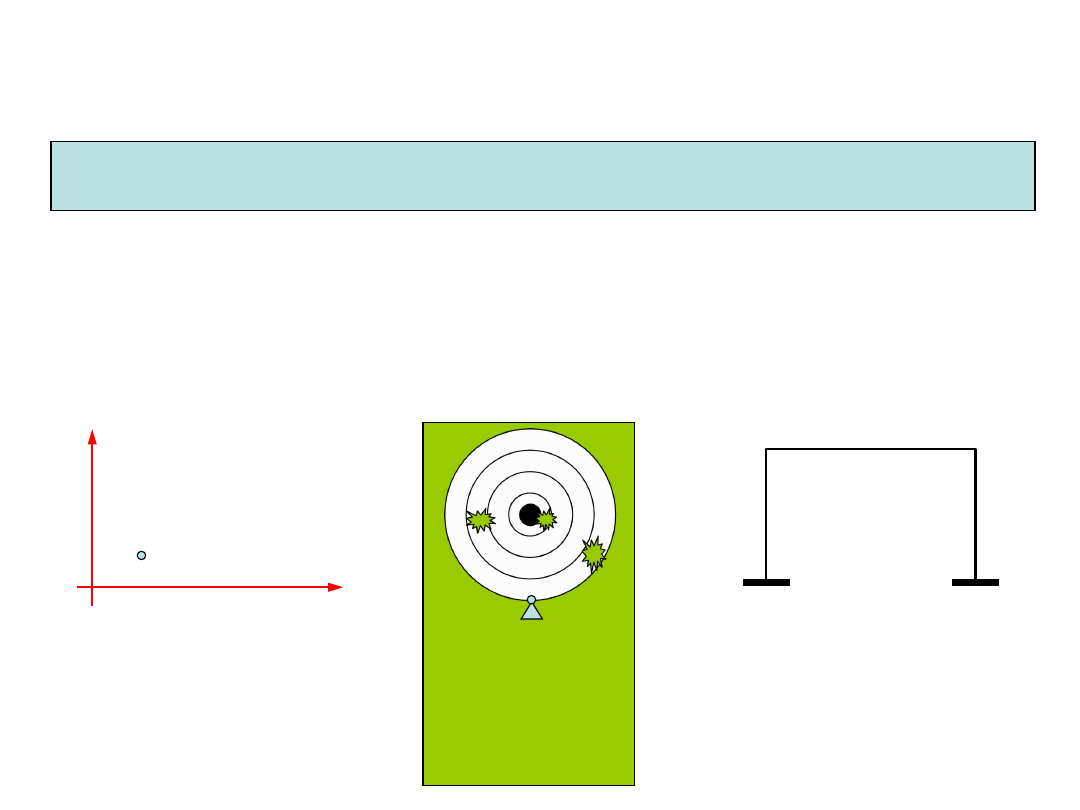
Punkt materialny na
płaszczyźnie posiada
2 stopnie swobody

(

)

x,y

y

x

Rama statycznie
niewyznaczalna
ma 0 stopni
swobody

Tarcza podparta
w jednym punkcie
ma 1 stopień
swobody

9

W problemach dynamiki
wprowadza się pojęcie
liczby stopni dynamicznej
swobody.

Rama w dynamice ma
nieskończenie wiele
stopni swobody

Rzeczywiste obiekty są ciałami odkształcalnymi. Wyznaczaniem ich ruchu
pod wpływem obciążeń zmiennych w czasie zajmuje się dynamika
konstrukcji

10

1.5. Metody dyskretyzacji

Dyskretyzacja – redukcja liczby stopni dynamicznej swobody (sds)

Metody:

– metoda mas skupionych
– metoda współrzędnych uogólnionych
– metoda elementów skończonych

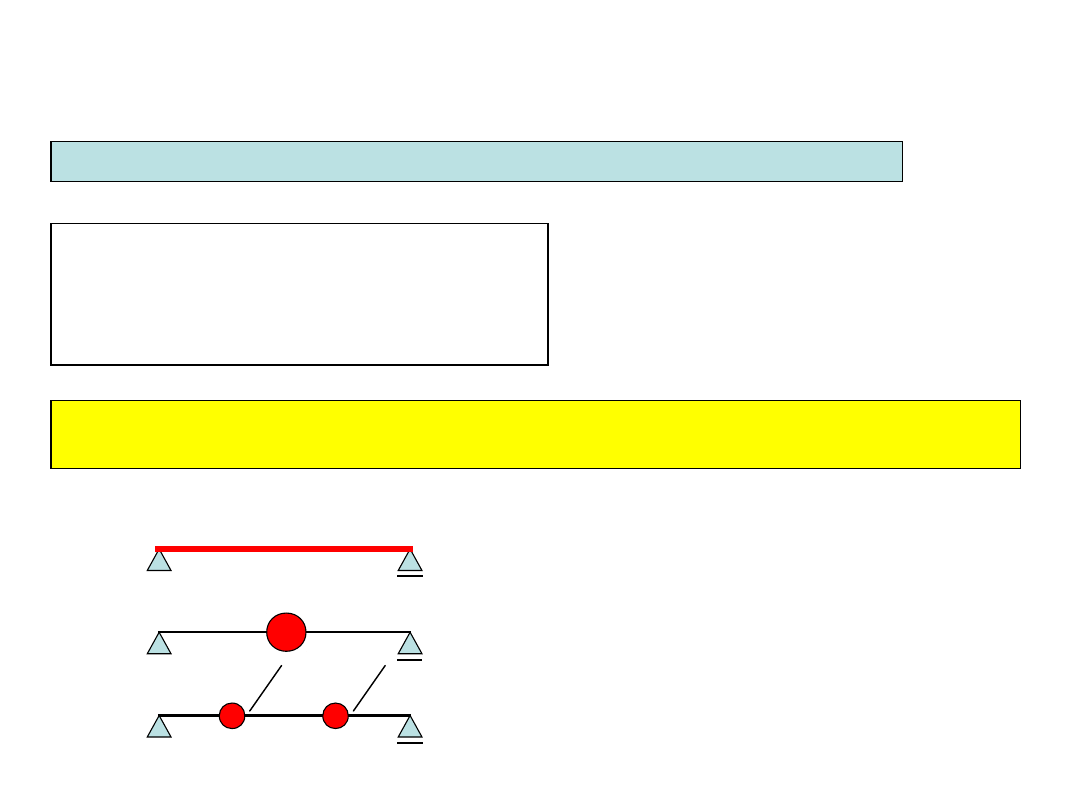
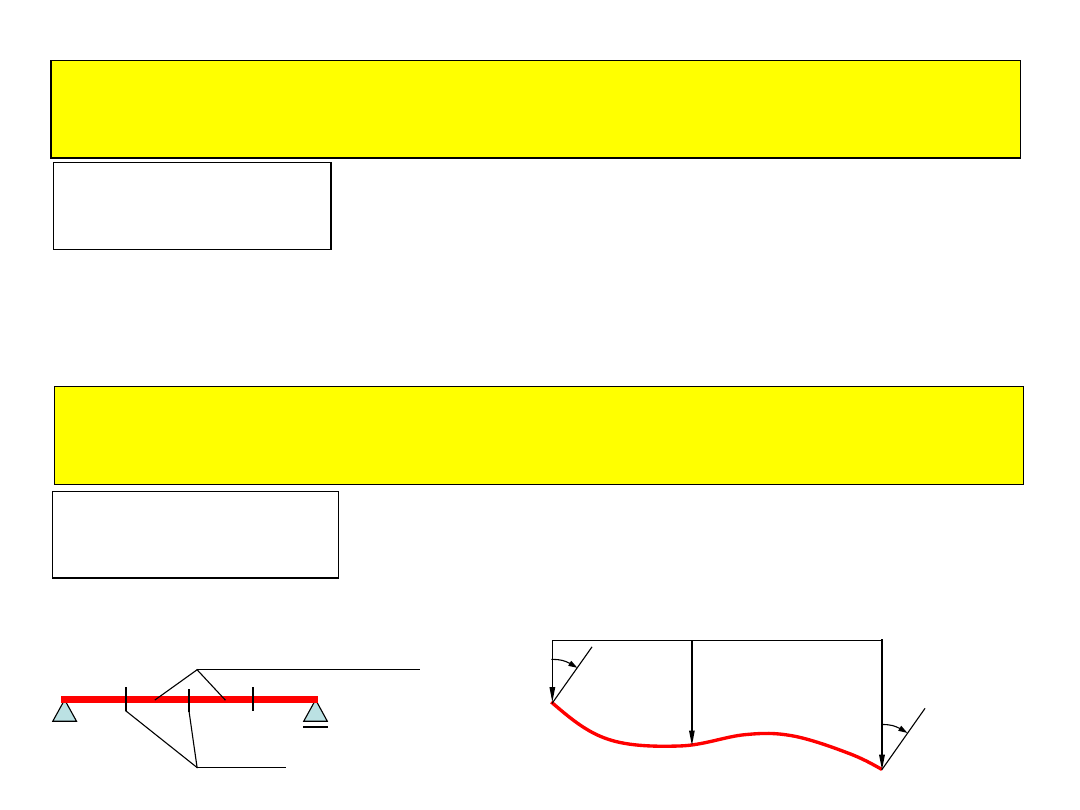
Metoda mas skupionych polega na zastąpieniu masy rozłożonej w sposób
ciągły zbiorem mas skupionych

belka z ciągłym rozkładem masy
(układ o nieskończonej liczbie sds)

belka z masą skupioną w jednym
punkcie
(układ o jednym sds)

belka z masą skupioną w dwóch
punktach
(układ o dwóch sds)

m

m

2

m

2

m

11

Metoda współrzędnych uogólnionych polega na opisie przemieszczeń
konstrukcji traktowanej jako układ ciągły za pomocą nieskończonego szeregu
postaci:

( )

( ) ( )

1

i

i

i

w x,t

v x q t

�

=

=

�

( )

w x,t

( )

i

v x

( )

i

q t

– funkcja przemieszczeń

– funkcje kształtu

– współrzędne uogólnione

W ww. szeregu uwzględnia się kilka pierwszych wyrazów i tym samym
dokonuje się redukcji liczby stopni dynamicznej swobody

W metodzie elementów skończonych dzieli się obiekt na elementy
skończone i opisuje się przemieszczenia wewnątrz każdego elementu
za pomocą funkcji:

( )

( ) ( )

4

1

i

i

i

w x,t

N x q t

=

=

�

( )

w x,t

( )

i

N x

( )

i

q t

– funkcja przemieszczeń wewnątrz
elementu

– funkcje kształtu

– przemieszczenia węzłowe

elementy skończone

węzły

( )

1

q t

( )

2

q t

( )

3

q t

( )

4

q t

( )

w x,t

Część 2

Siły działające na obiekty

13

2.1. Siły
zewnętrzne

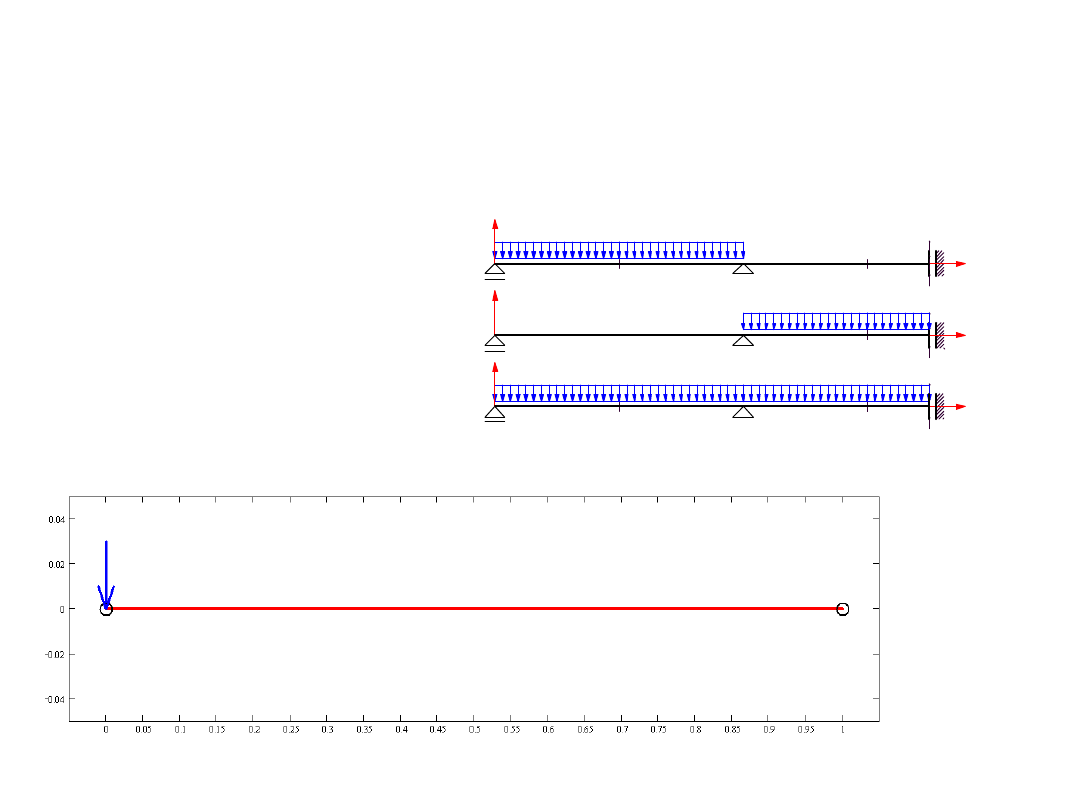
Obciążenia statyczne to obciążenia niezmienne w czasie lub
zmieniające się na tyle wolno, że nie wywołują drgań:

- obciążenia ciężarem własnym
- obciążenia użytkowe stałe
- obciążenia użytkowe zmienne

z

z

x

z

x

x

1

5

3

1

5

3

2

4

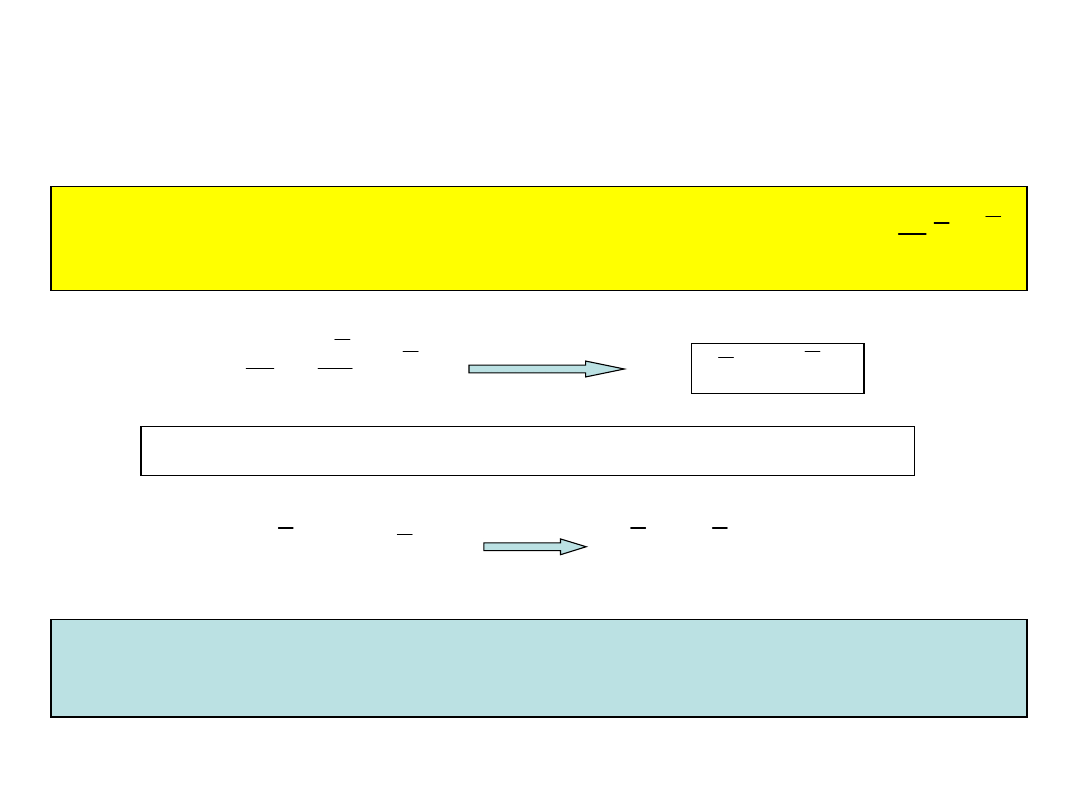
Obciążenie w przęsłach 1 i 3

1

5

3

2

4

2

4

Obciążenie w przęsłach 1 i 2

Obciążenie w przęśle 2

Przykład obciążeń użytkowych
zmiennych nie wywołujących
drgań

Przykład obciążenia ruchomego nie wywołującego
drgań

14

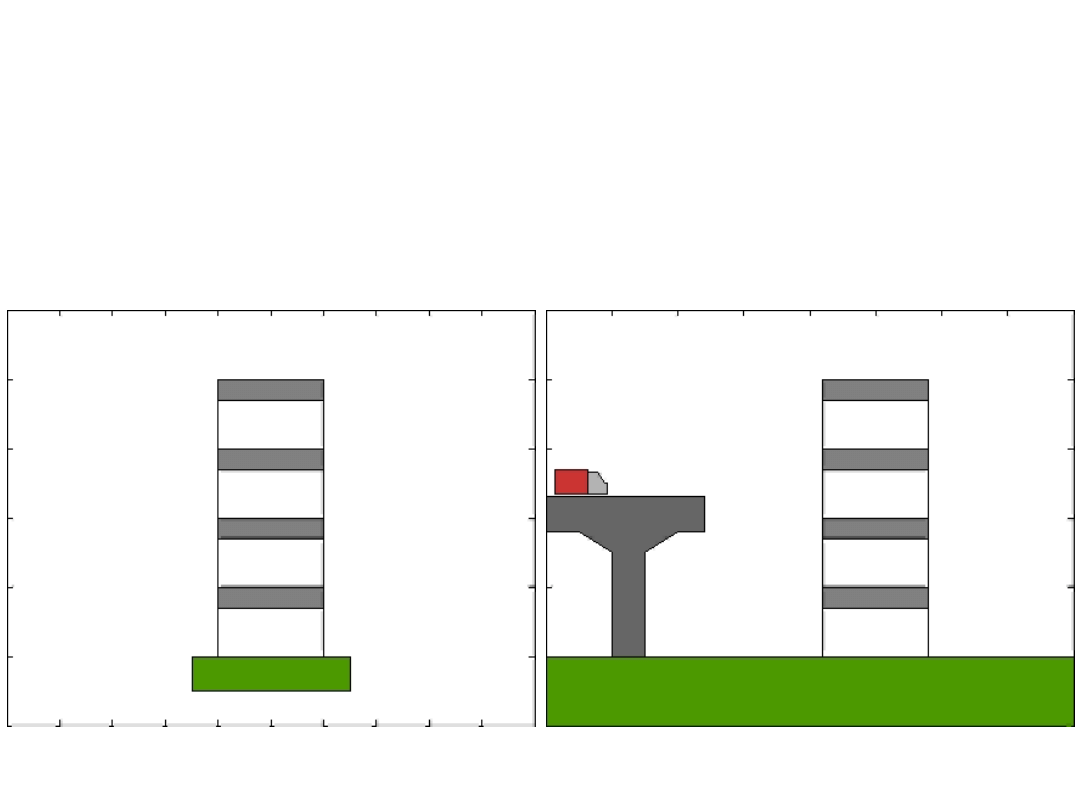
Obciążenia dynamiczne charakteryzuje szybka zmienność w czasie. Efektem
obciążeń dynamicznych są drgania obiektu.

- obciążenia wiatrem,
- obciążenia kinematyczne w trakcie trzęsienia ziemi,
- obciążenia dynamiczne związane z działalnością człowieka (ruch pojazdów,
praca maszyn itp.),
- obciążenia wyjątkowe o charakterze dynamicznym.

Autor: Paweł Szeptyński – student IV roku TKI (Studenckie Koło Naukowe Mechaniki Budowli)

15

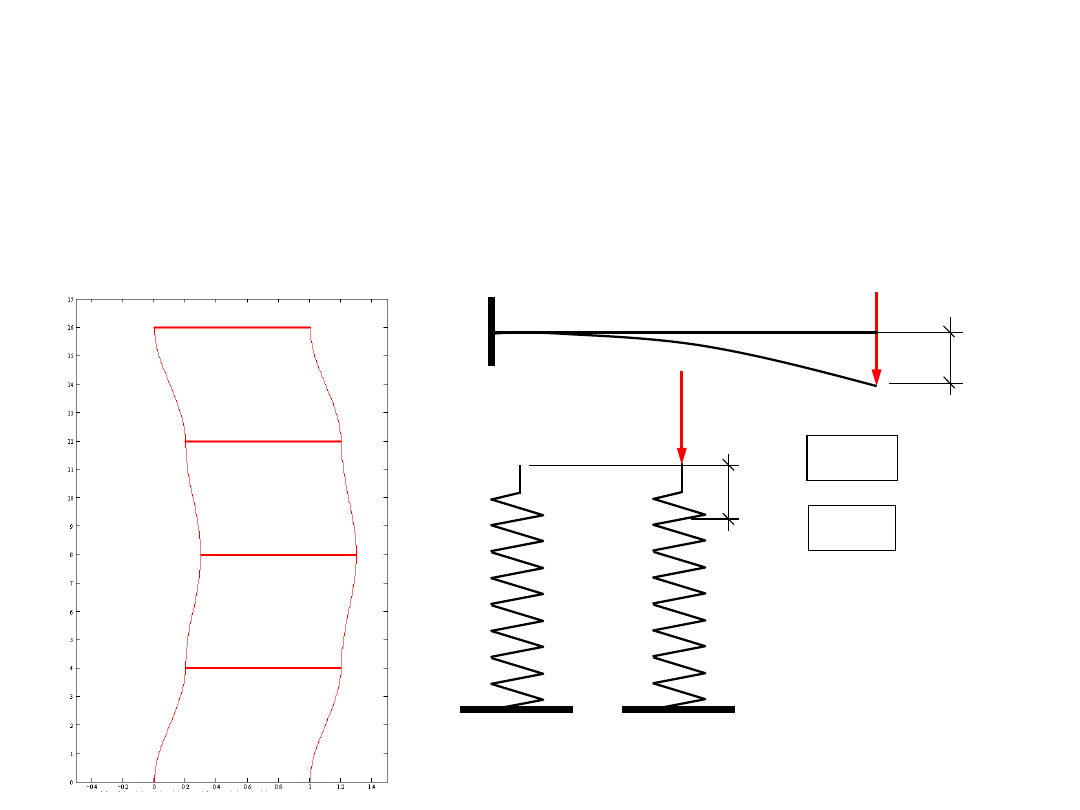
2.2. Siły sprężystego
oddziaływania

Obiekt pod wpływem obciążeń zewnętrznych ulega odkształceniu, które wiąże
się z powstawaniem sił wewnętrznych. Odkształcenia mogą być plastyczne lub
sprężyste. W dynamice przyjmuje się, że konstrukcja pod działaniem obciążeń
dynamicznych odkształca się sprężyście.

P

q

P

q

P kq

=

qδP

=

k

– współczynnik

sztywności



– współczynnik

podatności

Model więzów sprężystych

16

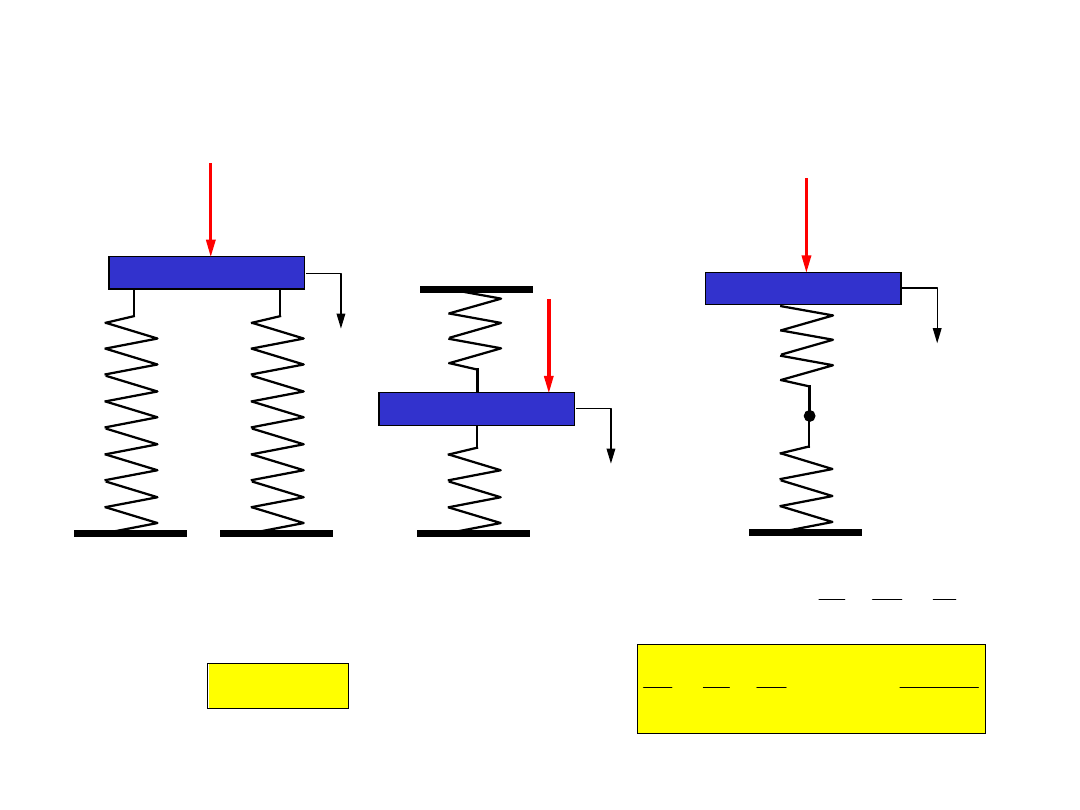
Zastępcze współczynniki
sztywności

1

k

2

k

P

q

1

k

2

k

P

q

1

k

2

k

P

q

(

)

1

2

1

2

1

2

P P P

k q k q

k k q

= + =

+

=

+

1

2

z

k

k k

= +

1

2

1

2

P

P

P

q q q

k

k

k

= + = +

=

1 2

1

2

1

2

1

1

1

z

z

kk

k

k

k

k

k k

= +

�

=

+

Równoległe połączenie sprężyn

Szeregowe połączenie sprężyn

17

2.3. Siły bezwładności

Siły bezwładności (siły d’Alemberta) występują wyłącznie w zagadnieniach
dynamiki.

Siły bezwładności mają zawsze zwrot przeciwny do zwrotu przyspieszenia,
jakiego doznaje punkt materialny.

Pozorne siły bezwładności rzeczywiście działają na ciała materialne
w układach nieinercjalnych. Siły te można mierzyć za pomocą
dynamometrów.

u

u

F

ma

=-

w

b

u

c

a

a

a

a

= -

-

w

u

c

ma

F F

F

= + +

c

c

F

ma

=-

b

F ma

=

- siła bezwładności Coriolisa

- siła rzeczywista

- siła bezwładności unoszenia

18

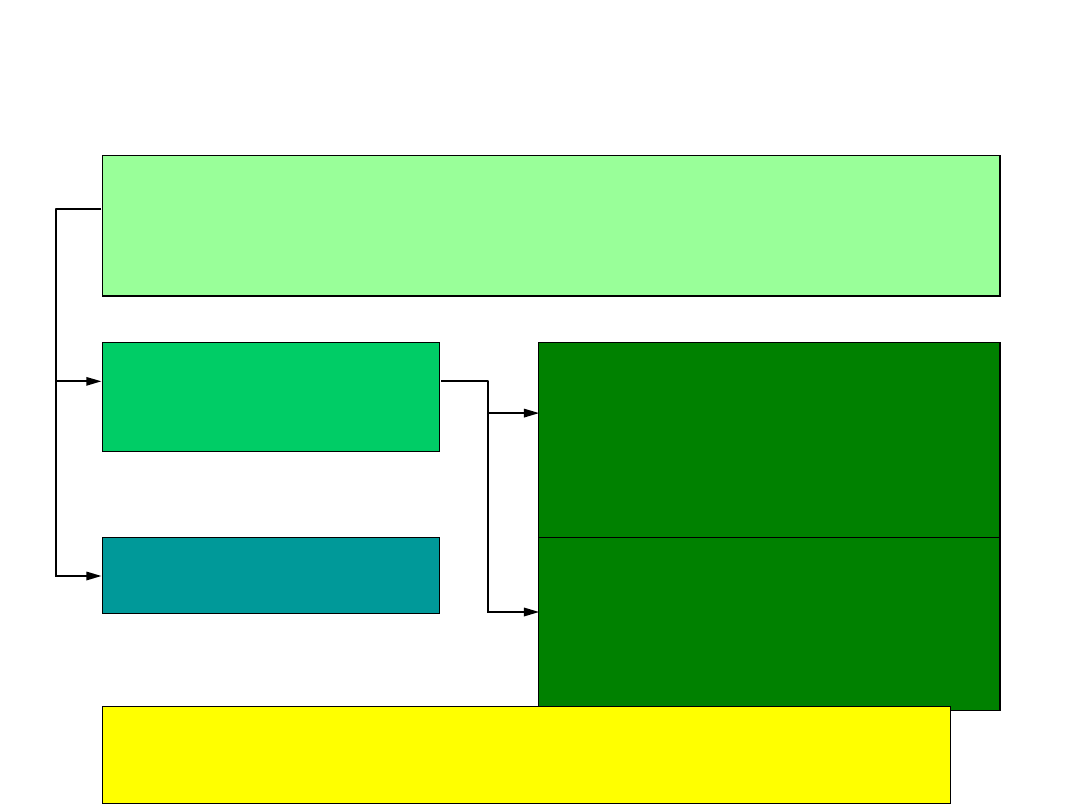
Tarcie wewnętrzne to całość zjawisk fizycznych
towarzyszących przemieszczaniu się względem siebie
elementów tego samego ciała i powodujących
rozpraszanie energii podczas ruchu. (Inaczej: tłumienie)

Tłumienie materiałowe
wywołane procesami
zachodzącymi w siatce
krystalicznej i w warstwie
międzykry-stalicznej. (tłumienie
konstrukcyjne)
Tarcie konstrukcyjne
polegające na rozpraszaniu
energii na powierzchniach styku
pomiędzy elementami
konstrukcyjnymi

Tarcie wewnętrzne

w ciałach

stałych

Tarcie wewnętrzne

w cieczach

2.4. Siły tłumienia, podstawowy model
tłumienia

Uwaga: Siła tarcia (tłumienia) występująca podczas ruchu ciała jest
siłą zewnętrzną czynną – jest oporem rozpraszającym energię
układu

19

Podstawowy model tarcia wewnętrznego - tłumienie
wiskotyczne

Wartość siły oporu wiskotycznego jest proporcjonalna do
prędkości a jej zwrot jest przeciwny do zwrotu wektora prędkości

R

( )

r t

&

R

r c

=- �

&

c

- współczynnik tłumienia

cαm

=

- współczynnik tłumienia w modelu, w którym zakłada się,
że tłumienie jest proporcjonalne do pędu masy
(w procesie tłumienia dominujący jest wpływ środowiska)

cβk

=

- współczynnik tłumienia w modelu, w którym zakłada się,
że tłumienie jest proporcjonalne do sztywności układu
(w procesie tłumienia dominujące znaczenie mają zjawiska
zachodzące w strukturze materiału konstrukcyjnego)

cαm

βk

=

+

- w kombinowanym wariancie tłumienia
wiskotycznego (model tłumienia Rayleigha)

Część 3

Równanie ruchu układu o jednym stopniu swobody

21

3.1. Druga zasada dynamiki Newtona w odniesieniu do
punktu
materialnego i zasada d’Alemberta

d

dr

m

F

dt

dt

�

�=

�

�

�

�

Aksjomat ruchu: Istnieją układy odniesienia, w których, jeżeli

na punkt materialny działa siła, to zmienia jego pęd według
prawa:

d

p F

dt

=

m const

=

( )

( )

mr t

F t

=

&&

( )

( )

x

x

mq t

F t

=

&&

( )

( )

y

y

mq t

F t

=

&&

( )

( )

z

z

mq t

F t

=

&&

( )

( )

B t

mr t

=- &&

( )

( )

0

F t

B t

+

=

Zasada d’Alemberta: W dowolnym położeniu punktu materialnego będącego

w ruchu suma sił czynnych i sił bezwładności jest równa 0.

22

3.2. Zasada d’Alemberta w odniesieniu do układu
punktów

1. Układ punktów materialnych jest ograniczony więzami geometrycznymi,

stacjonarnymi, dwustronnymi i gładkimi.

2. Na układ punktów materialnych działają

układy sił czynnych, reakcji i sił bezwładności:

i

i

i

i

i

i

F

R

B

,

,

A

A

A

� �

� �

� �

� �

� �

� �

���

1

1

1

0

0

0

i

i

i

n

n

n

F R B

F R B

F

R

B

� + + =

�

���

�

� + + =

�

����

�

� + + =

�

1

S

/δ

Si

/δ

Sn

/δ

1

1

1

0

n

n

n

i

Si

i

Si

i

Si

i

i

i

Fδ

R δ

B δ

=

=

=

� +

� +

� =

�

�

�

(

)

1

0

n

i

i

Si

i

F Bδ

=

+

� =

�

Założenia:

Zasada d’Alemberta w odniesieniu do układu punktów materialnych:
Spośród wszystkich możliwych ruchów układu punktów materialnych
poddanego działaniu więzów geometrycznych, stacjonarnych, dwustronnych i
gładkich tylko ten jest możliwy, w którym suma prac sił czynnych i
bezwładności na przemieszczeniach wirtualnych jest równa 0.

23

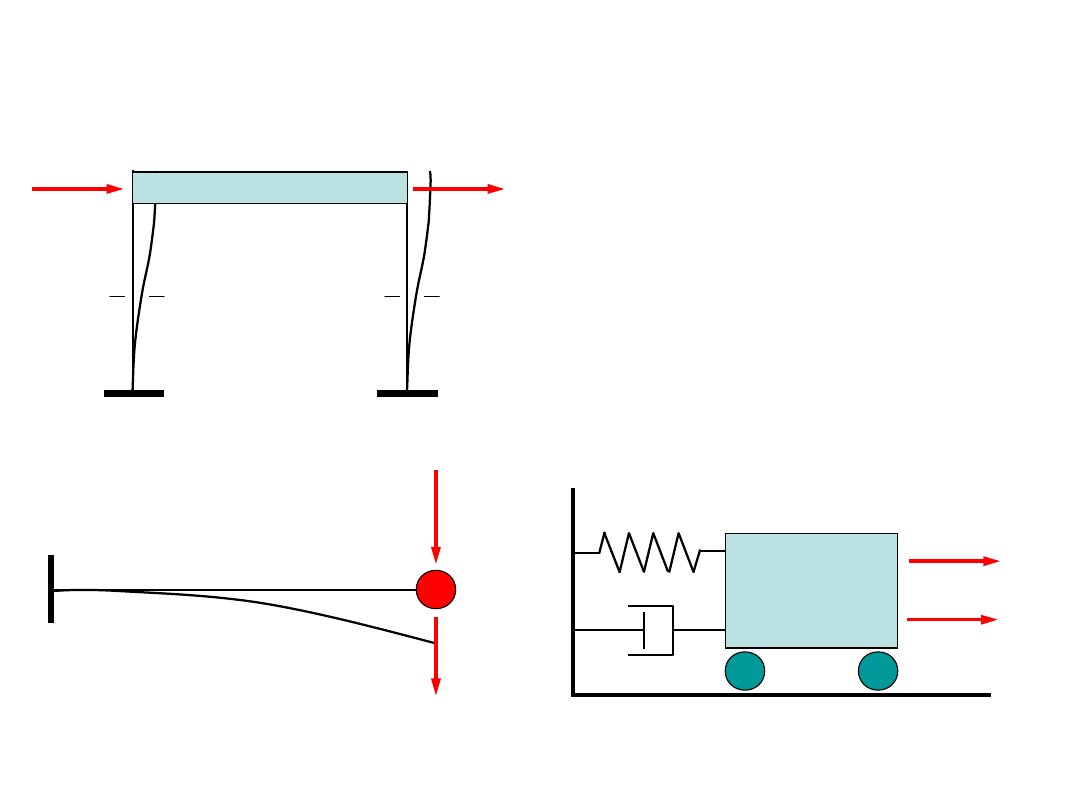
3.3. Obiekty o jednym stopniu dynamicznej swobody

( )

P t

( )

q t

2

k

2

k

m

Założenia:

1. Nieskończona sztywność

kondygnacji

2. Nieskończona sztywność

podłużna słupów

3. Małe, w odniesieniu do

wysokości słupów, wychylenia
masy.

Rama płaska ze sztywnym
ryglem

Wspornik z masą skupioną na
końcu

( )

P t

m

( )

q t

k, c

m

k

c

( )

P t

( )

q t

Model układu o jednym stopniu
swobody

2

c

2

c

24

( )

P t

( )

q t

m

Q

2

N

1

N

2

M

1

M

( )

2

k

q t

( )

2

k

q t

( )

2

c

q t

&

( )

2

c

q t

&

( )

mq t

&&

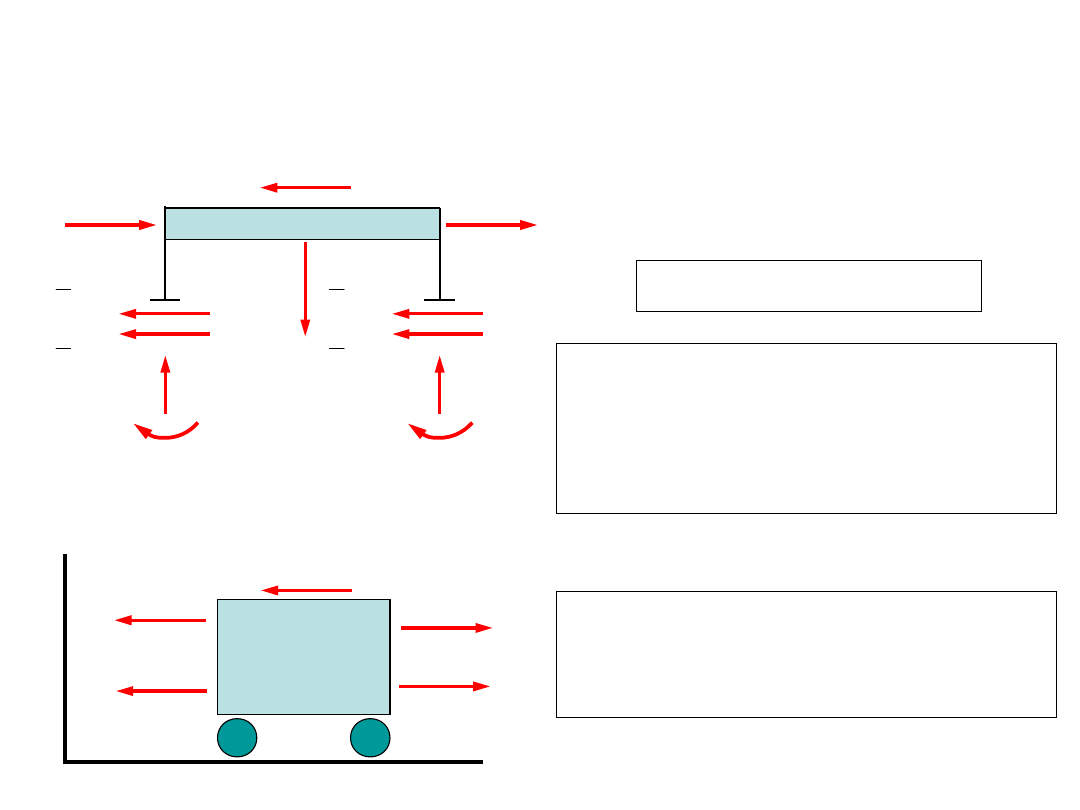
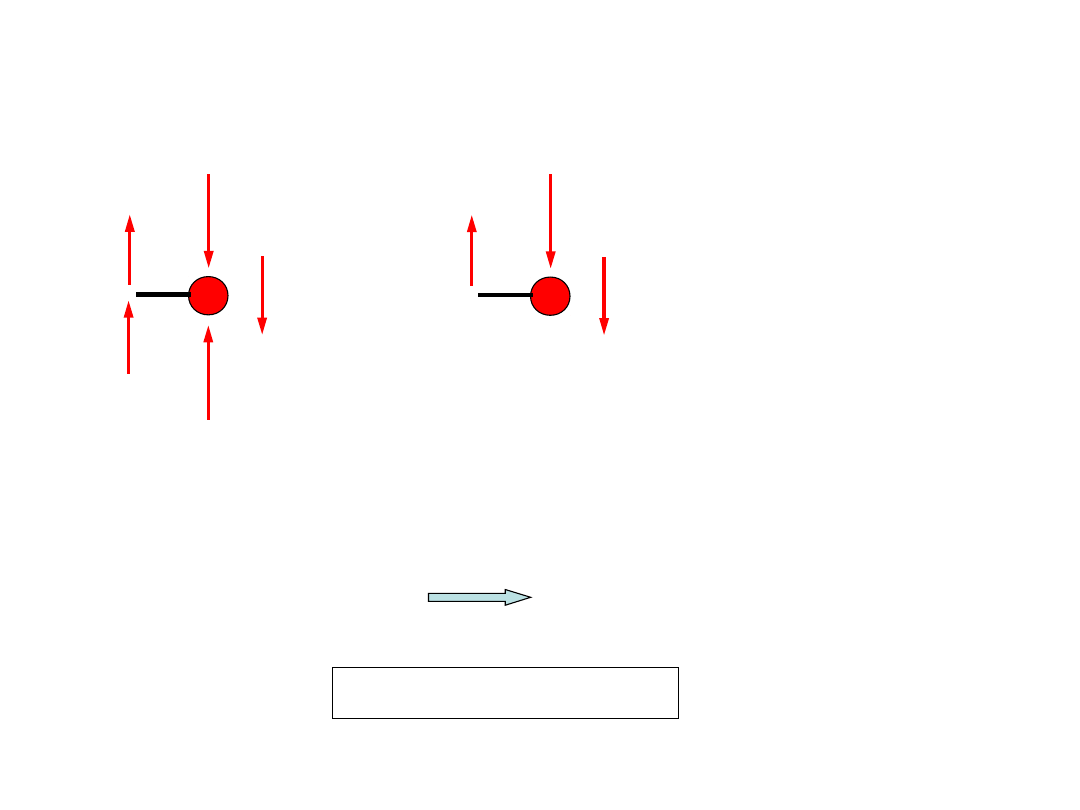
3.4. Konstrukcja równań ruchu

Myślowo wyizolowany rygiel ramy
płaskiej

Na podstawie zasady d’Alemberta:

( )

( )

( )

( )

mq t

cq t

kq t

P t

+

+

=

&&

&

m

( )

P t

( )

q t

( )

mq t

&&

( )

kq t

( )

cq t

&

Równanie ruchu układu materialnego
o jednym stopniu dynamicznej
swobody.

(Równanie różniczkowe niejednorodne
drugiego rzędu)

Równanie ruchu ma postać równania
równowagi sił na kierunku ruchu. Siły
N i M spełniają dwa pozostałe równania
równowagi.

Myślowo wyizolowana masa z
modelu układu o jednym stopniu
swobody

( )

( )

0

0

0

0

q

q , q

v

=

=

&

Warunki brzegowe :

25

( )

P t

%

( )

q t

%

m

( )

kq t

%

( )

cq t

&

%

( )

mq t

&&

%

st

P

st

q

m

st

kq

Myślowo wyizolowana masa skupiona
wspornika:

w ruchu

w położeniu równowagi statycznej

( )

( )

st

P t

P t

P

=

+

%

( )

( )

st

q t

q t

q

=

+

%

Równanie równowagi statycznej

st

st

kq

P

=

Równanie równowagi
dynamicznej

( )

( )

( )

( )

mq t

cq t

kq t

P t

+

+

=

&&

&

%

%

%

%

( )

( )

( )

(

)

( )

st

st

mq t

cq t

k q t

q

P t

P

+

+

+

=

+

&&

&

( )

( )

( )

( )

q t

q t

q t

q t

=

�

=

&

&&

%

&

%

&&

( )

( )

( )

( )

mq t

cq t

kq t

P t

+

+

=

&&

&