15. Zmienna losowa typu ciągłego.

Zmienna losowa X przyjmująca wartości z pewnego przedziału (albo przedziałów), dla której istnieje nieujemna funkcja f taka, że dystrybuantę F zmiennej losowej X można przedstawić w postaci

F(x)=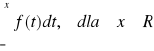

nazywamy zmienną losową ciągłą zaś funkcję f jej gęstością.

Uwaga Powiemy, że dany jest rozkład prawdopodobieństwa zmiennej losowej X typu ciągłego, jeżeli jest dana jej dystrybuanta F lub gęstość f.

Własności zmiennej losowej typu ciągłego:

Jeżeli x jest punktem ciągłości f, to

1. F'(x)=f(x),

2.

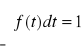
3.

4.

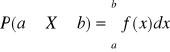
Przykład.

(1) Dla jakiej wartości parametru C funkcja f: R→R dana wzorem:
jest gęstością zmiennej losowej ciągłej X ?Wyznacz dystrybuantę zmiennej losowej X narysuj jej wykres oraz oblicz P(-1≤X≤1).

Oczywiście musi być C>0.

Ponadto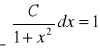
,

skąd

.

Ostatecznie
.

Wobec tego powyższa funkcja może być gęstością zmiennej losowej ciągłej dla
.

Jej wykres (rys. 13.5.1):

Wyznaczymy jej dystrybuantę.

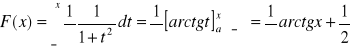
zaś rysunek 13.5.2 przedstawia jej wykres

Obliczmy
.

(2) Dla jakiej wartości parametru C funkcja f: R→R dana wzorem: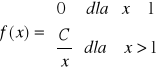
, gdzie
jest gęstością zmiennej losowej ciągłej X ?

Policzmy
. W tym przypadku nie można więc dobrać stałej C tak, aby powyższa funkcja stała się gęstością.

Wartością oczekiwaną zmiennej losowej ciągłej X nazywamy liczbę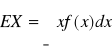

pod warunkiem, że całka
jest zbieżna.

Wariancją zmiennej losowej ciągłej X nazywamy liczbę D²X=E(X-EX)²= EX²-(EX)², , gdzie
.

Przykład

(1) Obliczyć wartość oczekiwaną i wariancję zmiennej losowej X, której gęstość dana jest wzorem: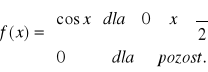
(wykres na rysunku 13.5.3).Oblicz

.

Policzymy wariancję zmiennej losowej . W tym celu musimy policzyć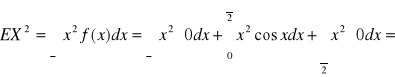

.

Ostatecznie mamy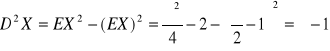
.

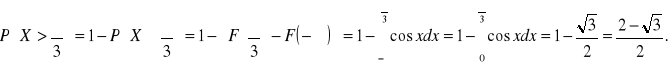
(2) Oblicz wartość oczekiwaną zmiennej losowej X, której gęstość dana jest wzorem:
.

Dla zmiennej losowej wartość oczekiwana a tym samym wariancja nie istnieje, ponieważ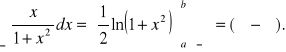
Symbol ∞-∞ jest nieoznaczony, więc nie można określić wartości oczekiwanej.

16. Rozkłady zmiennych losowych ciągłych

1. Zmienna losowa ma rozkład jednostajny (prostokątny lub równomierny) skoncentrowany na przedziale <a, b> jeżeli jej gęstość dana jest wzorem
,.

Dystrybuantą tej zmiennej losowej jest funkcja

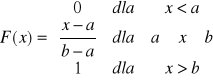
Wartość oczekiwana :EX=0,5(a+b)

Wariancja D²X=1/12(b-a)²

Przykład

Rozpatrzmy zmienną losową o rozkładzie jednostajnym , której gęstość jest stała w przedziale [1,5], natomiast poza nim jest równa zeru.

W przedziale [1,5] funkcja przyjmuje stałą wartość dodatnią C, wobec tego pole powstałego w ten sposób prostokąta musi być równe 1 (rysunek 13.5.10). Stąd (5-1)C=1 i
.

Wzór gęstości jest następujący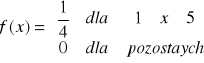
.

Dystrybuanta jest następująca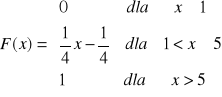
.

Prawdopodobieństwo, że zmienna losowa przyjmuje wartości z przedziału [2,7] jest równe
.

2.Zmienna losowa ciągła X ma rozkład wykładniczy o parametrze λ>0, jeżeli jej gęstość f jest postaci

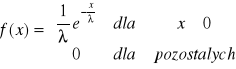
Łatwo obliczyć , że EX=λ, D²X=λ² oraz dystrybuanta

.

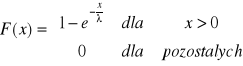
Przykład

Załóżmy, że długość rozmowy telefonicznej ma rozkład wykładniczy z parametrem λ=12. Jeśli ktoś zajmie budkę telefoniczną tuż przed tobą, jakie jest prawdopodobieństwo , że będziesz musiał czekać więcej niż 5 minut.

Przyjmując, że X jest zmienną losową określającą długość rozmowy telefonicznej. Musimy policzyć P(X>5), czyli

3.Zmienna losowa X ma rozkład normalny (rozkład Gaussa) o parametrach m∈R i σ >0 jeżeli jej gęstość wyraża się wzorem

,

Wartością oczekiwaną, rozkładzie Gaussa jest EX=m, natomiast wariancją
.

Na rysunku 13.5.16 są wykresy gęstości zmiennej losowej podlegającej rozkładowi normalnemu dla m=-1 i σ=1, m=0 i σ=1, m=1 i σ=2 oraz m2 i σ=2.

Fakt, że zmienna losowa X ma rozkład normalny o parametrach m i σ zapisujemy N~(m, σ) .

Jeśli N~(0, 1) wówczas zmienna losowa X ma standaryzowany rozkład normalny, którego gęstość wyraża się wzorem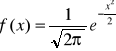
.

Przykład

(1) Zmienna losowa X podlega rozkładowi N(2,4). Obliczyć P(|X|>6).

Mamy P(|X|>6)=1-P(|X|≤6)=1-P(-6≤X≤6).

Standaryzując zmienną losową X i uwzględniając wzór Φ(-t)=1-Φ(t) otrzymujemy

P(-6≤X≤6)=P(
)=P(-2≤T≤1)= Φ(1)- Φ(-2)= Φ(1)-1+ Φ(2) ≈0,8186 czyli P(|X|>6) ≈1-0,8186=0,1816.

(2) Zmienna losowa X podlega rozkładowi N(1,2). Obliczyć P(|X|<2.4). Wyznaczyć stałą a tak aby P(|X-1|<a)≈0,95.

Mamy P(|X|<2.4)= P(-2.4<X<2.4)= P(
)=P(-1.7≤T≤0.7)= Φ(0.7)- Φ(-1.7)= Φ(1)-1+ Φ(1.7) ≈0.7134.

Mamy P(|X-1|<a)= P(-a<X-1<a)= P(-a+1<X<a+1)= P(
)=P(-0.5a≤T≤0.5a)= Φ(0.5a)- Φ(-0.5a)= Φ(0.5a)-1+ Φ(0.5a)=2Φ(0.5a)-1 ≈0.95.

Φ(0.5a)=0.975 czyli ostatecznie a≈3,9.

ZADANIA

1. Zmienna losowa X podlega rozkładowi według gęstości danej wzorem
   

Obliczyć stałą C. Wyznaczyć dystrybuantę zmiennej losowej X. Obliczyć P(1ႣXႣ2).

2. Zmienna losowa X podlega rozkładowi według gęstości danej wzorem
   

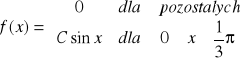
Obliczyć stałą C. Wyznaczyć dystrybuantę zmiennej losowej X. Obliczyć P(
ႣXႣ
).

3. Zmienna losowa X ma rozkład o gęstości

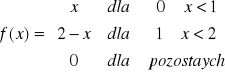
(a)Naszkicować wykres gęstości

(b)Wyznaczyć i naszkicować dystrybuantę tego rozkładu

4. Zmienna losowa X przyjmuje dowolną wartość z przedziału <1,3>. Zakładając, że rozkład prawdopodobieństwa tej zmiennej jest jednostajny, podać gęstość, dystrybuantę oraz obliczyć P(1,4ႣXႣ2).

5. Pociągi kolejki elektrycznej odjeżdżają ze stacji co 5 minut. Zakładając, że rozkład czasu przybycia pasażera na stację jest jednostajny, obliczyć wartość oczekiwaną i wariancję czasu oczekiwania na pociąg.

6. Zapałkę o długości 5cm złamano w dowolnym punkcie. Zakładając, że rozkład prawdopodobieństwa długości krótszej części zapałki jest jednostajny, oblicz prawdopodobieństwo, że długość krótszej części zapałki nie przekracza 0,5 cm.

7. Czas bezawaryjnej pracy pewnego urządzenia (w godz.) jest zmienną losową o rozkładzie wykładniczym z parametrem ၬ=2. Oblicz prawdopodobieństwo, że awaria nastąpi po5 godzinach pracy tego urządzenia. Oblicz wartość przeciętną ilości godzin po których nastąpiła awaria.

8. Załóżmy, że długość rozmowy telefonicznej ma rozkład wykładniczy z parametrem
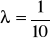
   . Jeżeli ktoś zajmie budkę telefoniczną tuż przed tobą, jakie jest prawdopodobieństwo, że będziesz musiał czekać:

(a)więcej niż 10 minut

(b)od 10 do 20 minut

9. Zmienna losowa X podlega rozkładowi N(5,2). Obliczyć P(X<3,6).

• Zmienna losowa X podlega rozkładowi N(2,4). Obliczyć P(|X|>6).

• Zmienna losowa X podlega rozkładowi N(1,2). Obliczyć P(|X|<2,4). Wyznaczyć stałą a tak aby P(|X-1|<a)Ⴛ0,95.

• Zmienna losowa X podlega rozkładowi N(3,5). Obliczyć P(|X-1|Ⴓ1.

• Niech zmienna losowa X ma rozkład N(
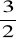
  ,2). Obliczyć prawdopodobieństwo(X<2,5), P(X>-0,5), P(0,5<X<2), P(|2X-1|<1), P(|X|>0,5).

• Pewien automat produkuje części, których długość jest zmienną losową o rozkładzie N(2,0.2) (w cm). Wyznaczyć prawdopodobieństwo otrzymania braku, jeśli dopuszczalne długości części powinny zawierać się w przedziale (1.7,2.3).

---