Ćwiczenie 8. Podstawowe systemy dyskretne, ich charakterystyki i przykłady zastosowań

8.1. Cele ćwiczenia

Celem ćwiczenia jest bliższe zapoznanie się z trzema podstawowymi systemami dyskretnymi: transformatorem Hilberta, filtrem różniczkującym i filtrem grzebieniowym, ich charakterystykami i niektórymi zastosowaniami do przetwarzania sygnałów dyskretnych.

8.2. O sposobie osiągania celów ćwiczenia

W ramach przygotowania do ćwiczenia student:

• odświeży wiedzę z wykładu z PCPS z poprzedniego semestru na temat różnych sposobów opisu systemów dyskretnych, zwłaszcza na temat charakterystyk czasowych i częstotliwościowych tych systemów,

• odświeży wiedzę na temat obliczania odpowiedzi systemu FIR (od ang. finite impulse response) na dowolne pobudzenie (splot dyskretny, mnożenie transformat DTFT),

• skorzysta z zalecanej literatury [1], [2] na temat badanych w ćwiczeniu systemów dyskretnych,

• zapozna się uważnie z treścią niniejszej instrukcji,

• przygotuje pisemne rozwiązania problemów postawionych w instrukcji, przyniesie je na zajęcia laboratoryjne celem porównania wyników obliczeń teoretycznych z wynikami obliczeń komputerowych i dołączy do sprawozdania.

8.3. Podstawy teoretyczne

System różniczkujący, nazywany również filtrem różniczkującym, to taki system, którego odpowiedź jest pochodną pobudzenia. Idealny dyskretny system różniczkujący o opóźnieniu wynoszącym
odstępów próbkowania, pobudzony sygnałem dyskretnym
pochodzącym z równomiernego próbkowania, z okresem T, nieznanego sygnału analogowego
tak, że
, ma za zadanie dostarczenie na wyjście sygnału:

(1)

W systemie dyskretnym sygnał
jest znajdowany bez odtwarzania sygnału analogowego
. Oczywiście, byłoby pożądane, gdyby opóźnienie
było równe zeru. W praktyce tak jednak nie jest, dlatego uwzględniamy to opóźnienie w opisie systemu różniczkującego.

Charakterystyka amplitudowo-fazowa idealnego systemu różniczkującego, realizującego funkcję (1) jest następująca:

(2)

Łatwo sprawdzić, że charakterystyka amplitudowa tego systemu narasta liniowo, gdy częstotliwość
zmienia się od 0 do ½. Z tego powodu system różniczkujący wykorzystuje się do uwypuklania składowych wysokoczęstotliwościowych w widmie sygnału.

Odpowiedź impulsową idealnego systemu (2) znajdujemy za pomocą odwrotnego dyskretno-czasowego przekształcenia Fouriera (DTFT) w następujący sposób [3]:

,
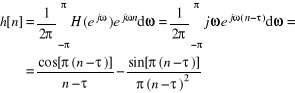
(3)

Dla
=0 (system o zerowym opóźnieniu) z (3) otrzymujemy

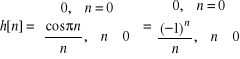
(4)

a dla
(system z wyprzedzeniem o pół odstępu próbkowania) dostajemy

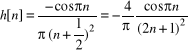
(5)

Obie powyższe odpowiedzi impulsowe są antysymetryczne, przy czym dla systemu (4)

,
(6a)

a dla systemu (5)

,
(6b)

W obu przypadkach odpowiedź idealnego systemu różniczkującego jest obustronnie nieskończona, tzn. próbki
są różne od zera dla
aż do nieskończoności. A więc idealny system różniczkujący nie jest realizowalny.

Transformator Hilberta jest szeroko wykorzystywany praktycznie, zwłaszcza w cyfrowych systemach telekomunikacyjnych. Służy on do przekształcania sygnału rzeczywistego o widmie amplitudowym symetrycznym względem częstotliwości zerowej, czyli parzystym, na sygnał zespolony, nazywany również sygnałem analitycznym (przez analogię do odpowiadającego mu sygnału z czasem ciągłym), lub hilbertowskim, o widmie prawostronnym, tzn. równym zeru dla ujemnych częstotliwości. Transformator Hilberta wykorzystuje się w systemach radarowych, w systemach przetwarzania sygnałów mowy, systemach z modulacją, z efektywnym zespolonym próbkowaniem sygnałów rzeczywistych pasmowych [4].

Idealny dyskretny transformator Hilberta ma charakterystykę amplitudowo-fazową zdefiniowaną wzorem

(7a)

gdzie
jest funkcją znaku, a
ma takie samo znaczenie, jak poprzednio. Wzór (7a) można równoważnie zapisać w postaci

(7b)

Odpowiedź impulsowa systemu idealnego (7) wyraża się wzorem [4]:

,
(8)

Jest ona obustronnie nieskończona, a więc nie jest realizowalna. Dla
=0 z (8) otrzymujemy

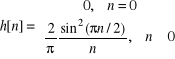
(9)

gdzie
spełnia warunek (6a), a co druga próbka jest zerowa:
. Natomiast dla
dostajemy

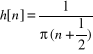
(10)

gdzie
spełnia warunek (6b), ale próbki
są niezerowe. Zauważmy, że gdy
=0, to wzór (7b) reprezentuje idealny przesuwnik fazy o
.

Zespolony sygnał hilbertowski. Jeżeli na wejście transformatora Hilberta (7b), przy
=0, podamy sygnał rzeczywisty
o widmie dwustronnym
, to na jego wyjściu otrzymamy sygnał
o następującym widmie:

(11)

Utwórzmy sygnał zespolony hilbertowski

(12)

Stanowi on sumę oryginalnego sygnału rzeczywistego
i odpowiedzi
transformatora Hilberta na
, potraktowanej jako składowa urojona sygnału y[n].

Rys.1. Filtr zespolony hilbertowski;
jest transformatą Hilberta rzeczywistego sygnału wejściowego
o widmie dwustronnym, a na wyjściu otrzymuje się sygnał zespolony
+j
o widmie prawostronnym.

Sygnał
jest, rzecz jasna, zespolony i ma widmo

(13)

Podstawiając (11) do (13) dostajemy

(14)

Oznacza to, że sygnał
ma widmo prawostronne. System przekształcający dany sygnał rzeczywisty
na sygnał zespolony (12) taki, że składowa urojona
jest transformatą Hilberta składowej rzeczywistej, nazywamy filtrem zespolonym (hilbertowskim). Schemat blokowy tego filtru przedstawia rys.1.

Przykład. Jeżeli
i a=const, to
i, konsekwentnie,
. Jeżeli
, to mamy do czynienia z widmem
i
, gdzie
jest deltą Diraca.

Aproksymacja FIR. Oba systemy idealne, system różniczkujący i transformator Hilberta, można z dowolną dokładnością aproksymować za pomocą realizowalnego systemu FIR lub IIR (od ang. infinite impulse response). Dalej zajmiemy się wyłącznie liniowo-fazowymi systemami FIR. Będziemy rozważać system FIR o odpowiedzi impulsowej
,
o skończonej długości (liczbie próbek) N i charakterystyce amplitudowo-fazowej

(15)

System FIR (15) ma dokładnie liniową charakterystykę fazową, gdy

,
(16a)

lub, gdy

,
(16b)

W tym ćwiczeniu mamy do czynienia z systemami FIR o antysymetrycznej odpowiedzi impulsowej, a więc wchodzi w grę wzór (16b). Niemniej, w obu przypadkach, opóźnienie
wnoszone przez filtr wynosi
odstępów próbkowania.

Systemy o uogólnionej charakterystyce fazowej. Jeżeli N jest nieparzyste, to
jest antysymetryczna względem próbki o numerze n=
. Ta sytuacja odpowiada rozpatrzonemu wyżej przypadkowi
=0, ale z dodatkowym opóźnieniem o całkowitą liczbę
odstępów próbkowania.

Jeżeli N jest parzyste, to
jest antysymetryczna względem punktu na osi n w połowie odcinka pomiędzy próbkami o numerach: n=
i n=
. Ta sytuacja odpowiada rozpatrzonemu wyżej przypadkowi
, ale z dodatkowym opóźnieniem o całkowitą liczbę
odstępów próbkowania. Oznacza to, że odpowiedź impulsową idealnego (dalej wykorzystywanego w metodzie okien) systemu o opóźnieniu
takim samym, jak w docelowym systemie FIR, można otrzymać za pomocą wzorów (4) i (9) dla N nieparzystych i za pomocą wzorów (5) i (10) dla N parzystych. Wystarczy tylko przesunąć
na osi n w prawo o
odstępów dla N nieparzystych i o
odstępów dla N parzystych (działa tu twierdzenie o przesunięciu dla DTFT). Ze wzoru (16b) wynika też, że dla N nieparzystych
oraz, że
. Natomiast dla N parzystych jedynie
. To z kolei oznacza, że system nie przenosi składowej stałej (wyzerowuje ją).

W praktyce nie zawsze jest pożądana aproksymacja w całym pasmie pulsacji
. Nieraz wystarcza aproksymacja w pasmie ograniczonym do
, gdzie
nazywamy częstotliwością odcięcia (od ang. cutoff). Wówczas idealne charakterystyki amplitudowo-fazowe (2) i (7), które mamy aproksymować liniowo-fazowym systemem FIR o długości N, zapiszemy w postaci

(17)

dla systemu różniczkującego i

(18)

dla transformatora Hilberta. Za
podstawiliśmy faktyczne opóźnienie równe
odstępy próbkowania. Tu
jest największą częstotliwością, dla której aproksymacja ma być dobra. Częstotliwość
nazywamy również szerokością pasma systemu. Poza pasmem
zwykle nie specyfikuje się wymagań na charakterystykę częstotliwościową systemu, chociaż można by to uczynić, np. narzucając warunek, że
dla
. Dodajmy, że charakterystyki (17) i (18) reprezentują systemy idealne o tzw. uogólnionej charakterystyce fazowej [1], z uwagi na obecność czynnika
.

Metoda okien należy do elastycznych i z tego powodu popularnych metod aproksymacji. W tej metodzie odpowiedź impulsową
docelowego systemu FIR otrzymujemy w następujący sposób. Mnożymy odpowiedź impulsową idealną
projektowanego systemu o uogólnionej charakterystyce fazowej (tu odpowiadającą charakterystyce (17) lub (18), a więc odpowiednio przesuniętą na osi n, co wcześniej przedyskutowaliśmy) przez funkcję okna
o długości docelowego systemu FIR, zdefiniowaną dla n=0,1,...,N-1. Wykonujemy więc działanie

(19)

W ten sposób ograniczamy długość odpowiedzi impulsowej systemu do realizowalnej, przyczynowej, N-punktowej. Najprościej jest, rzecz jasna, zastosować okno prostokątne (ang. boxcar)

(20)

Jest to równoważne obcięciu nieskończonej odpowiedzi impulsowej
symetrycznie względem n=
. Jednakże, jak można się przekonać eksperymentalnie za pomocą interfejsu systdys w tym ćwiczeniu, okno prostokątne wnosi niepożądane zafalowania do charakterystyki amplitudowej systemu FIR. Jest tak dlatego, że efektowi obcięcia ogonów odpowiedzi impulsowej
towarzyszy zjawisko Gibbsa, znane z teorii szeregów Fouriera o skończonej liczbie wyrazów. To samo zjawisko można również wyjaśnić przenosząc wzór (19) do dziedziny częstotliwości. Oznacza to splot kołowy widma okna prostokątnego

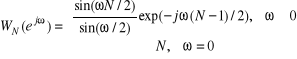
(21)

z charakterystyką amplitudowo-fazową
systemu idealnego. Splot ten ma postać

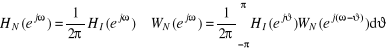
(22)

Widmo amplitudowe okna (moduł (21)) nie jest gładkie. Występują w nim zafalowania. Na skutek tego, w wyniku splotu kołowego również pojawiają się zafalowania. Oprócz tego następuje rozmycie charakterystyki amplitudowej w otoczeniu nieciągłości charakterystyki idealnej, np. wokół
dla transformatora Hilberta. Jest ono tym większe, im szerszy jest listek główny widma okna. Aby zmniejszyć zafalowania, zamiast okna prostokątnego stosuje się okna łagodnie opadające w kierunku krańców, do
i
. Do najpopularniejszych okien należy okno von Hanna [1], [2]

(23)

Inne znane okna są dostępne za pośrednictwem interfejsu graficznego systdys.

Przykład. Obliczymy odpowiedź impulsową
systemu różniczkującego FIR o długości N=7, z oknem prostokątnym i z oknem von Hanna. Ponieważ N jest nieparzyste, skorzystamy ze wzoru (4):
. Ta odpowiedź impulsowa jest nieprzyczynowa. Aby była przyczynowa, tak samo jak funkcja okna przez którą mamy ją pomnożyć, należy ją przesunąć o (N-1)/2 w prawo. Docelowy FIR z oknem prostokątnym ma w rezultacie odpowiedź impulsową
i tu
, ponieważ dla okna prostokątnego
. Natomiast system FIR z 7-punktowym oknem von Hanna o postaci
ma odpowiedź impulsową wyrażoną następująco:

. Zwróćmy uwagę, że tu
. Oczywiście, zero na początku i końcu można pominąć, a więc faktycznie ten drugi system jest N=5 - punktowy, o odpowiedzi impulsowej
.

Filtr grzebieniowy służy przede wszystkim do wycinania z widma danego sygnału niepożądanych, okresowych składowych szumów i zakłóceń, np. częstotliwości sieci energetycznej 50Hz i harmonicznych tej częstotliwości. Ma on oprócz tego inne interesujące zastosowania, np. do przetwarzania muzyki [2]. Filtr grzebieniowy można zrealizować na różne sposoby: jako system FIR lub IIR [2]. W tym ćwiczeniu, w interfejsie systdys oprogramowano dwa grzebieniowe filtry FIR o transmitancjach:

filtr grzebieniowy 1 (24)

filtr grzebieniowy 2 (25)

Długość odpowiedzi impulsowej każdego z tych filtrów wynosi
. Częstotliwości wycinane przez te filtry, to:

filtr grzebieniowy 1 (26)

filtr grzebieniowy 2 (27)

W programie demonstracyjnym cw08ch wykorzystano filtr grzebieniowy 1, ale o transmitancji
unormowanej tak, że
.

8.4. Narzędzia programowe

W ćwiczeniu wykorzystuje się zestaw napisanych w MATLABie programów komputerowych dostępnych za pośrednictwem interfejsu graficznego z wywołaniem
systdys. Interfejs graficzny jest przeznaczony do prezentacji charakterystyki amplitudowej systemu różniczkującego FIR i transformatora Hilberta FIR projektowanych metodą okien oraz do obserwacji charakterystyki amplitudowej dwóch filtrów grzebieniowych. Oczywiście, do syntezy filtrów grzebieniowych (24) i (25) okien się nie wykorzystuje (są niepotrzebne). Projektant, oprócz wyżej wymienionych typów systemów, ma do wyboru: rząd filtru grzebieniowego, długość odpowiedzi impulsowej i częstotliwość odcięcia
systemu różniczkującego, i transformatora Hilberta. Również, dla systemu różniczkującego i transformatora Hilberta wybierana jest funkcja okna. Dwa okna: Kaisera i Czebyszewa, wymagają zadania parametru. Okno Czebyszewa w MATLABIE 4 w laboratorium może mieć długość tylko nieparzystą. Aktualizacja wykresu charakterystyki amplitudowej może odbywać się automatycznie lub ręcznie, za pośrednictwem myszy. Dostęp do siatki ułatwiającej odczytanie szczegółów wykresu i do rozciągania wybranych fragmentów, odbywa się za pośrednictwem poleceń
grid i
zoom. Z menu Plik eksportowany jest do obszaru roboczego MATLABa plik o nazwie wspolczsys, zawierający odpowiedź impulsową aktualnie badanego systemu dyskretnego. Można go odczytać przez nazwę pod znakiem zachęty:
wspolczsys. Oprócz tego w zestawie ćwiczenia znajduje się niezależny program z wywołaniem
cw08ch, napisany w MATLABie, demonstrujący przetwarzanie sygnału w badanych systemach.

8.5. Przygotowanie do ćwiczenia

5.1. Oblicz odpowiedź impulsową przyczynowego systemu różniczkującego FIR o długości N=3 z oknem prostokątnym i z oknem von Hanna o długości N=5. Porównaj wyniki.

5.2. Powtórz obliczenia z p.5.1 dla transformatora Hilberta.

5.3. Oblicz sygnał
na wyjściu idealnego transformatora Hilberta (7b) z
, pobudzonego sygnałem
([2] str.570) i znajdź odpowiadający mu zespolony sygnał hilbertowski y[n] (12).

5.4. Napisz wzór zamknięty na odpowiedź impulsową
filtru grzebieniowego
.

5.5. Oblicz charakterystykę amplitudową
powyższego filtru (z p.5.4) i naszkicuj ją dla N=8. Oznacz osie i wyskaluj.

5.6. Znajdź odpowiedź tego samego filtru z p. 5.5 na pobudzenie sygnałem
,
,
i zapisz tę odpowiedź w postaci
. Skorzystaj ze wzorów trygonometrycznych:
,
. Ile wynoszą: b i
? Dla jakich
sygnał na wyjściu filtru grzebieniowego
? Jak powinna wyglądać charakterystyka amplitudowa idealnego odpowiednika rozważanego tu filtru grzebieniowego, by wprowadzał on jak najmniej zniekształceń do użytecznej części widma przetwarzanego sygnału? Nanieś taką idealną charakterystykę innym kolorem na wcześniej naszkicowaną
.

5.7. Które ze składowych sygnału

(28)

zostaną usunięte przez filtr grzebieniowy 1, o rzędzie N=8, a które zostaną przeniesione przez ten filtr? Jaki sygnał
otrzymamy faktycznie na wyjściu tego filtru, a jaki powinien on być, gdyby filtr grzebieniowy był idealny?

8.6. Eksperymenty laboratoryjne

6.1. Korzystając z interfejsu systdys (rys.2) zbadaj charakterystyki amplitudowe systemu różniczkującego o długości nieparzystej, N=51, i o najbliższej długości parzystej, N=50. Przyjmij
=0.5. Wybierz okno prostokątne i okno von Hanna. Zaobserwuj różnice dotyczące maksymalnej wielkości zafalowań i kształtu charakterystyki w otoczeniu częstotliwości f=0 i f=1/2, w porównaniu z charakterystyką idealną. Zanotuj wyniki obserwacji w sprawozdaniu. Możesz, oczywiście, zilustrować te wyniki rysunkami. Wyeksportuj do obszaru roboczego MATLABa plik ze współczynnikami systemu różniczkującego z oknem von Hanna N=51 i zapisz go w pamięci za pomocą poleceń:
firoz51=wspolczsys; save firoz51 firoz51. Powtórz to samo dla systemu z N=50; tu utwórz plik firoz50.

6.2. Powtórz badania z p.6.1 dla transformatora Hilberta. Wyeksportowane pliki nazwij: fihil51 fihil50.

6.3. Korzystając dalej z interfejsu systdys zbadaj charakterystyki amplitudowe filtrów grzebieniowych 1 i 2 dla N=8 i dla N=7. Naszkicuj je. Zanotuj wycinane częstotliwości i porównaj z wynikami z odpowiednich wzorów ((26) i (27)) z p.8.3 tej instrukcji, i z wynikami swoich obliczeń z p.5.3. Skorzystaj z możliwości rozciągnięcia wykresu i wprowadzenia siatki pisząc zoom i grid w oknie MATLABa pod znakiem zachęty
. Jakie istotne różnice występują dla N parzystych i dla N nieparzystych? Zwróć uwagę na wartości charakterystyki amplitudowej dla
i dla
.

6.4. Sprawdź wyniki swoich obliczeń z p.5.1 i 5.2 porównując je z zawartością plików ze współczynnikami odpowiednich systemów wyeksportowanych z systdys do obszaru roboczego MATLABa.

6.5.1. Załaduj pliki ze współczynnikami systemu różniczkującego i transformatora Hilberta:
load fihil51,
load firoz51. Uruchom program cw08ch za pomocą polecenia:

cw08ch(512, 1024, 5*10^(-4), 1, 128, 0.1, fihil51, firoz51, 8)

Kolejne parametry tego programu-funkcji to: L, długość sygnału świergotowego (ang. chirp)

(29)

wykorzystanego do demonstracji filtracji hilbertowskiej i różniczkowania, liczba punktów FFT do obliczania widma, współczynnik
świergotu (29), amplituda świergotu a, iloczyn
częstotliwości środkowej świergotu i L, współczynnik skalujący wartości próbek szumu addytywnego z generatora liczb losowych o rozkładzie równomiernym w przedziale [0,1], dodanego do świergotu, pliki współczynników i rząd filtru grzebieniowego.

Dalej zajmiemy się eksperymentem ilustrowanym na Fig.2 do 7. Fig.2 do 4 to ilustracje dla transformatora Hilberta, a Fig.5 do 7 ilustrują system różniczkujący. Kolejne „figury” (od Fig.3 wzwyż) mają wpisane pauzy (ang. pause) i dlatego pojawią się na ekranie po raz pierwszy dopiero po naciśnięciu enter.

Eksperyment z transformatorem Hilberta. Fig.2a prezentuje wejściowy sygnał świergotowy
, a Fig.2b pokazuje sygnał na wyjściu transformatora Hilberta. Idealny odpowiednik tego sygnału wyraża wzór

(30)

Fig.2c pokazuje przebieg błędu, czyli różnicy pomiędzy sygnałem idealnym (30) i sygnałem z Fig.2b, otrzymanym z transformatora Hilberta fihil51 o odpowiedzi impulsowej z Fig.2d. Chwilowa wartość bezwzględna błędu jest tu bardzo mała, gdyż użyty tu system FIR jest stosunkowo długi. Fig.3 przedstawia widma amplitudowe odpowiednich sygnałów: a) wejściowego rzeczywistego świergotu o widmie dwustronnym, b) za transformatorem Hilberta, c) za filtrem zespolonym hilbertowskim - widmo praktycznie prawostronne i d) widmo idealnego sygnału zespolonego:

(31)

do porównania z Fig.3c. Widać, że różnice są niewielkie. Fig.4a pokazuje różnicę widm fazowych na wyjściu i na wejściu transformatora Hilberta. Różnica ta odzwierciedla fakt przesunięcia fazy sygnału wyjściowego względem wejściowego o minus
dla częstotliwości dodatnich (czynnik
we wzorze (7b)) i o plus
dla częstotliwości ujemnych (czynnik
we wzorze (7b)). Fig.4b przedstawia charakterystykę fazową transformatora Hilberta - przesuwnika fazy. Dla lepszej czytelności wykresu usunięto składnik liniowo-narastający występujący we wzorach (7b) i (18).

Eksperyment z systemem różniczkującym. Fig.5a i b pozwalają porównać pochodną świergotu z Fig.2a, otrzymaną za pomocą filtru różniczkującego firoz51, ze świergotem zróżniczkowanym idealnie, tj.

(32)

Wartość bezwzględna błędu (Fig.5c) jest tu również mała, ale nieco większa niż dla transformatora Hilberta. Zauważmy też, że zafalowania przebiegu błędu różniczkowania sygnału świergotowego odzwierciedlają zafalowania charakterystyki amplitudowej użytego systemu dyskretnego. Te ostatnie obserwowaliśmy na Fig.1 korzystając z interfejsu systdys. Fig.5d pokazuje antysymetryczną odpowiedź impulsową użytego tu 51-punktowego filtru różniczkującego z centralną próbką zerową. Fig.6 przedstawia odpowiednie widma amplitudowe i fazowe. Widmo amplitudowe pochodnej świergotu (Fig.6a i c) odzwierciedla narastający przebieg charakterystyki amplitudowej filtru różniczkującego. Wysokie częstotliwości świergotu zostały uwypuklone. Fig.7 prezentuje standardowy eksperyment z różniczkowaniem fali trójkątnej, typowy dla testowania filtrów różniczkujących. Widać, że błąd różniczkowania jest największy tam, gdzie występują załamania („ostrza”) sygnału wejściowego. Widać też, że w sygnale wyjściowym, zróżniczkowanym, występują tam przerzuty. Rozciągnij sygnał na Fig.7b i zanotuj maksymalną wartość przerzutu. Porównasz ją w p.6.5.2 z przerzutem dla systemu różniczkującego o długości parzystej.

Pozostałe wykresy (Fig.8 do 11) dotyczą filtru grzebieniowego i zajmiemy się nimi dalej, w p.6.5.3.

6.5.2. Powtórz kolejno powyższe obserwacje dla transformatora Hilberta i systemu różniczkującego o parzystej długości N=50:
load fihil50,
load firoz50,
cw08ch(512, 1024, 5*10^(-4), 1, 128, 0.1, fihil50, firoz50, 8). Porównaj wartości przerzutów fali prostokątnej na wyjściu filtru różniczkującego o długości N=51 i o długości 50. Porównaj również odpowiedzi impulsowe użytych w eksperymentach systemów o długości parzystej i nieparzystej. Jakie są różnice?

6.5.3. Eksperyment z filtrem grzebieniowym. Teraz zajmiemy się dalszą częścią eksperymentu z filtrem grzebieniowym 1, o rzędzie N=8, z Fig.8 do 11. Jego odpowiedź impulsowa jest na tyle prosta, że jest generowana wewnątrz programu demonstracyjnego. Jest ona pokazana na Fig.8b. W tym miejscu porównaj tę odpowiedź impulsową z obliczoną w p.5.4. Powinny być identyczne.

W dalszej części eksperymentu powyższy filtr grzebieniowy przetwarza sygnał
opisany wzorem (28) i pokazany na Fig.9c. Stanowi on sumę sygnału pożądanego
z Fig.9a i zakłócenia
(Fig.9b). Wynik filtracji pokazuje Fig.9d, gdzie wycięto N/2 próbki początkowe i N/2 próbki końcowe (stany przejściowe). Jaki wzór opisuje sygnał
na Fig.9d? Sprawdź obliczenie np. dla n=100, albo 101, rozciągając wykres. Tu uwaga, próbki na Fig.9 są numerowane w konwencji MATLABa, a więc od n=1, zamiast od n=0. Na Fig.10 pokazano widma amplitudowe sygnałów z Fig.9 w skali liniowej, w tym samym układzie. Przyjrzyj się uważnie tym wykresom. Fig.11 przedstawia widma sygnałów tego eksperymentu, ale unormowane w taki sposób, by wartość maksymalna widma amplitudowego byłą równa 1. Fig.11b pokazuje wycinanie niepożądanych składowych przez filtr grzebieniowy. Splot realizowany przez filtr grzebieniowy jest równoważny mnożeniu widma sygnału
przez charakterystykę częstotliwościową filtru grzebieniowego. W rezultacie widmo sygnału
z Fig.11d jest bardzo zbliżone do widma pożądanego sygnału
z Fig.11a, a zakłócenia są odfiltrowane.

Literatura uzupełniająca

[1] Oppenheim A.V., Schafer R.W. with Buck J.R.: Discrete-Time Signal Processing. Prentice Hall 1999, transformator Hilberta: str.789-795 (p.11.4), filtr różniczkujący: str.482-485 (p.7.3.2).

[2] Orfanidis S.J.: Introduction to Signal Processing. Prentice Hall 1996, transformator Hilberta: str.542-543, filtr różniczkujący: str.542-543, 569-570 problems 10.3 i 10.8, i filtry grzebieniowe: str.253-258 (p.6.4.3), str. 293, str.404-416 (p.8.3.2), str. 601-603 (p.11.5) i ich zastosowania: str.355-360 (p.8.2.2).

[3] Rabiner L.R. and Schafer R.W.: On the behavior of minimax relative error FIR digital differentiators. The Bell System Technical Journal, vol. 53, No. 1, January 1974, str.333-361 (str.334-335 do wykorzystania w laboratorium).

[4] Rabiner L.R. and Schafer R.W.: On the behavior of minimax FIR digital Hilbert transformers. The Bell System Technical Journal, vol. 53, No. 2, February 1974, str.363-390 (str.364-365 do wykorzystania w laboratorium).

Rys.2. Okno interfejsu graficznego systdys

Imię i Nazwisko ................................................... Data ............................................

Nr grupy ...............................................................

Nr komputera .......................................................

Sprawozdanie z ćw. 8. Podstawowe systemy dyskretne, ich charakterystyki i przykłady zastosowań

Wyniki obliczeń

5.1. System różniczkujący.

Okno prostokątne, N=3

Okno von Hanna, N=5

2. Transformator Hilberta.

Okno prostokątne, N=3

Okno von Hanna, N=5

3. Sygnał na wyjściu idealnego transformatora Hilberta
   =

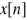
Odpowiadający mu zespolony sygnał hilbertowski y[n]=

5.4. Filtr grzebieniowy

5.5. Charakterystyka
=

Wykres dla N=8

5.6.
=

b=
=

Sygnał na wyjściu filtru grzebieniowego
dla
=

7. Filtr grzebieniowy 1, o rzędzie N=8, usunie z sygnału

składowe o pulsacjach:

a przeniesie

Na wyjściu tego filtru otrzymamy faktycznie sygnał
=

Gdyby filtr grzebieniowy był idealny, to na wyjściu tego filtru powinien być sygnał
=

Wyniki obserwacji

6.1.

6.2.

6.3.

6.4.

6.5.

Laboratorium PCPS Ćw. 8. Podstawowe systemy dyskretne, ich charakterystyki

i przykłady zastosowań E. Hermanowicz 9/11

Transformator

Hilberta

---