Wykład 1
Czym jest statystyka?
statystyka jest to zbiór metod służących do :
pozyskiwania
prezentacji
analizie danych.
Celem stosowania tych metod jest otrzymywanie, na podstawie danych użytecznych, uogólnionych informacji na temat zjawiska, którego dane dotyczy.
Proces pozyskiwania danych ogólnie jest nazywany badaniem statystycznym
Przykład
Badanie przeprowadzone przez ankieterów wśród pewnej grupy osób.
Badanie twardości materiału.
W ramach badania statystycznego dokonuje się obserwacji statystycznej.
Podstawowe zadania statystyki
analiza, która sprowadza się do sumarycznego opisu zbiory danych, a wykorzystane do tego celu środki nazywa się metodami opisu statystycznego
interpretacją danych
Pojecie statystyki matematycznej
W wielu rzeczywistych sytuacjach zebranie wszystkich potencjalnych danych nie jest możliwe, a interpretacji dokonuje się na podstawie odpowiednio zebranych danych częściowych, a badanym zjawiska. Taka analiza wykorzystująca metody rachunku prawdopodobieństwa nosi miano STATYSTYKI MATEMATYCZNEJ
Populacja generalna
Badania statystyczne dotyczą zawsze pewnej zbiorowości, której elementami są obiekty materialne, lub zjawiska. W statystyce matematycznej badaną zbiorowość statystyczna nazywa się populacją generalną lub zbiorowością generalną.
Populacja generalna skończona - jeśli zbiór jej elementów jest skończony.
Przykład
Zbiorowość studentów 2-go roku kierunku WT
Populacja generalna nieskończona - dotyczy zazwyczaj zjawiska, a nie obiektów materialnych.
Przykład
Zbiorowość wyników pomiarów twardości materiału.
Cechy statystyczne
Elementem populacji generalnej mogą mieć różne właściwości i najczęściej miewają, które podlegają obserwacji. Te właściwości nazywa się cechami statystycznymi lub krótko cechami.
Przykład
W badaniach populacji ludzi np. wiek, wzrost, płeć, kolor włosów
Cechy ilościowe - da się określić lub wyrazić: (wzrost, waga) są to cechy mierzalne
lecz własności jakościowe jak (płeć , kolor włosów) to są cechy niemierzalne
Przeważająca część metod statystycznej matematyki dotyczy analizy cech mierzalnych.
Rozkład cech - jeżeli elementy różnią się między sobą wartościami analitycznej cechy to mówi się o rozkładzie cechy w populacji.
Badania pełne i częściowe
Celem badania statystycznego na ogół jest poznanie rozkładu interesującej nas cechy w populacji generalnej oraz uzyskanie informacji o wartościach statystycznych charakterystyk parametrów tego rozkładu.
Rozróżnia się dwa zasadnicze typy badań
pełne - obejmujące wszelkie elementy zbiorowości generalnej
częściowe - obejmujące części elementy zbiorowości generalnej
Próba - podzbiór elementów populacji generalnej podlegająca badaniu nazywa się próbką. Statystyka matematyczna zajmuje się tylko badaniami częściowymi, takim, w których dobór próby podlega pewnym obiektywnym regułom.
Dobór próby - próba losowa
Próbę otrzymaną w wyniku doboru losowego nazywa się próbą losową.
Warunki dla zapewnienia losowego doboru próby.
Każdy element populacji generalnej ma dodatnie znane prawdopodobieństwo znalezienia się w próbie losowej.
Istnieje możliwość ustalenia prawdopodobieństwa znalezienia się w próbce dla każdego zespołu elementów populacji.
Ocena wielkości błędów wynikających z przeprowadzenia częściowego badania statystycznego jest możliwa tylko przy losowym doborze próby, w którym o fakcie znalezienia się poszczególnych elementów populacji w próbie decyduje przypadek.
Podstawowym zagadnieniem pojawiającym się w badaniach częściowych jest możliwość uogólnienia uzyskanych na podstawie próby wyników na całą populację oraz oszacowanie popełnionych przy tym błędów. Takie działanie nazywa się wnioskowaniem statystycznym.
Wyróżnia się 2 podstawowe typy problemów.
estymację (szacowanie)
sprawdzanie(weryfikacja) hipotez
Cechy skokowe i ciągłe
Cechy statystyczne (mierzalne), które przyjmują wartości całkowite nazywa się skokami lub dyskretnymi. Cechy przyjmujące wartości rzeczywiste nazywa się cechami ciągłymi.
Empiryczny rozkład cechy - stanowi podstawę dla wszystkich analiz badanej cechy.
Jeżeli próba dotycząca jednej cechy mierzalnej nie jest zbyt liczna tzn. dotyczy =<30 jednostek to występuje jej opracowanie polegające (na uszeregowaniu w porządku rosnącym danych liczb. Otrzymamy w ten sposób ciąg liczb - nazywa się szeregiem pozycyjnym
Wyniki „surowe” 4,5,0,1,2,4,0,9,4,5
po uporządkowaniu - szeregu pozycyjnego 0,0,1,2,4,4,4,5,5,9;
Jeżeli liczebność próby jest duża (orientacyjnie >30) to pierwszym etapem jest uszeregowanie szeregu pozycyjnego, a dopiero drugim etapem dokonanie grupowania, czyli klasyfikacji.
Grupowanie polega na podziale próby na podzbiory zwane grupami lub klasami, a wartością reprezentacyjną poszczególne klasy są ich środkami.
Przedziały klasowe oraz ich liczebności, czyli liczby jednostek próby należących do danej klasy tworzy razem tzw. szereg rozdzielczy.
001 |
2 |
444 55 |
9 |
poszczególne wartości klasowe dotyczące
np. badania (wyników) statystycznych
x1 - x2 - klasa
![]()
- środek klasy Histogram
Aby utworzyć szereg rozdzielczy należy:
ustalić obszar zmienności R badanej cechy czyli przedział ograniczony najmniejszym i największym elementem próby R = Xmax + Xmin
Xmax - największy element próbie
wyznaczyć liczbę przedziałów klasowych m próby o liczebności n
Nie ma szczegółowych zasad dotyczących podziału na klasy istnieje natomiast kilka segregacji dotyczących liczby przedziału klasowych m próby o liczebności n
liczba przedziałów klasowych nie powinna być mniejsza niż 7 i większa niż 15
liczebność w każdym przedziale nie powinna być mniejsza niż 5
sposoby określenia m (liczba klas musi się mieścić )
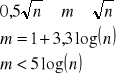
m - musi być zawsze liczbą całkowitą !
podzielić obszar zmienności na klasy i ustalić reprezentację klasy (środek podziału klasowego) oraz końce przedziałów klasowych
![]()
- szerokość przedziału
wektor brzegów (końców) przedziałów:
Xbk = Xmin + (k-1) ⋅ dd
k = 1...m + 1
wektor środków przedziałów klasowych
Xp:
Xpj = ![]()
(Xbj + Xbj +1)
j = 1...m
wyznaczyć liczebność w klasach (od 0 do n)
fj → w mathcad hist (Xb,X)
wyznaczyć prawdopodobieństwo empiryczne
![]()
j = 1...m m - liczba przedziałów
zbudować histogram
Zmiana losowa - to wielkość, która w wyniku doświadczenia przyjmuje określaną wartość zmianą po zrealizowaniu doświadczenia, a nie dająca się przewidzieć przez jego realizacją.
Def:
Zmienna losowa - jest to taka zmienna która w wyniku doświadczenia przybiera jedną i tylko jedną wartość ze zbioru tych wszystkich wartości, jakie ta zmienna może przyjąć.
Oznaczenie zmiennych losowych
1. Na ogół końcowymi literami alfabetu np. X, Y..............,
2. Wartości zmiennej losowej (realizująca) oznaczenie małymi literami np. x, y............,
Z wartościami zmiennej losowej związane są określone prawdopodobieństwa tak, więc zmienna losowa przybiera różne wartości z różnych prawdopodobieństwa.
D(X=xi)=pi - funkcja rozkładu prawdopodobieństwa
![]()
Funkcja ta charakteryzuje się tym, że suma prawdopodobieństw jest równa jedności
Rodzaje zmiennych losowych
zmienne skokowe (dyskretne)
zmienne ciągłe
Zmiennymi losowymi skokowymi (dyskretne) nazywa się takie zmienne losowe, które mają skończoną lub przeliczalny zbiór wartości.
Zmiennymi losowymi ciągłymi nazywa się takie zmienne losowe, które mogą przybierać dowolne wartości liczbowe pewnego przedziału liczbowego.
Rozkład zmiennej losowej:
Niech X jest zmienną losową dyskretną, która może przyjmować wartości x1, x2, ... odpowiednio z prawdopodobieństwem p1, p2, ... Każdej X przyporządkowane jest pewne prawdopodobieństwo. To prawdopodobieństwo można traktować jako funkcję określoną w zbiorze wartości, jakie może przyjmować zmienna losowa X
Określenie:
Rozkładem skokowej (dyskretnej)
Formy rozkładu:
tabeli
x x1 x2
p p1 p2
analitycznej
P(X=xi) = f(xi)
Funkcja rozkładu prawdopodobieństwa
graficzna: wykres
Wykład 2
Dystrybuanta zmiennej losowej (skumulowane prawdopodobieństwo)
Dystrybuantą zmiennej losowej nazywa się funkcję oznaczoną przez F(x), określoną
F(x) = P(X<x)
Określa ona prawdopodobieństwo tego, że zmienna losowa X przyjmuje jakąkolwiek wartość mniejszą od z góry przyjętej danej wartości x.
Dystrybuanta może być określona w przedziale ograniczonym lub jednostronnie, dwustronnie nieograniczonym.
Wartości w przedziale <a,b>:
jest funkcją nie malejącą
jest funkcją co najmniej lewostronnie ciągłą
F(a) = 0, F(b) = 1 (wartości w granicach)
Znając dystrybuantę F(x) można obliczyć prawdopodobieństwo tego, że zmienna losowa przyjmuje jakąś wartość leżącą pomiędzy wartościami: x1i x2:
P(x1 ≤ X < x2) = F(x2) - F(x1)
Dystrybuantę można także stosować dla znalezienia prawdopodobieństwa zdarzenia takiego, że badana zmienna losowa X przyjmuje wartość większą równą x. Ponieważ badane zdarzenie jest przeciwne zdarzeniu z prawdopodobieństwem F(x), to:
P(X ≥ x) = 1 - F(x)
Zmienna losowa ciągła
Zakładając, że wartości X przyjmowane przez zmienną losową X, zmieniają się w sposób ciągły w przedziale <a,b>, otrzymuje się granicę:
![]()
pochodna zmiennej losowej ciągłej jest równa jej funkcji gęstości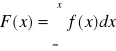
w przypadku, gdy f(x) jest określona dla x∈<a,b> to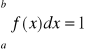
prawdopodobieństwo, że zmienna losowa ciągła przyjmuje jakąkolwiek wartość zawartą pomiędzy dowolnymi dwiema wartościami x1 < x2 można obliczyć na podstawie znajomości jej dystrybuanty lub jej funkcji gęstości
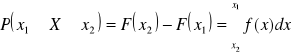
wzór ten określa to prawdopodobieństwo przyjęcia przez zmienną losową ciągłą pewnej konkretnej wartości x1 jest równa 0, gdyż 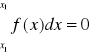
Rozkłady teoretyczne zmiennej losowej dyskretnej
Podstawowe rozkłady:
jednopunktowe
dwupunktowe
równomierne
Odszukać dla w/w następujące informacje:
funkcja rozkładu
dystrybuanta
E(x) - wartość oczekiwana
D2(x) - wariancja
σx - odchylenie standardowe
Rozkład dwumianowy - Bernouliego
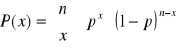
n - liczba naturalna
x = 0, 1...n
p - liczba rzeczywista p∈ (0,1)
wartość oczekiwana (średnia): E(x) =n⋅p
wariancja: D2(x) = n⋅p⋅ (1-p)
Rozkład Poissona
Jeżeli zmienne losowe X1, X2,...,Xn mają rozkład dwumianowy o parametrach n i ![]()
(λ = const > 0) to ciąg funkcji prawdopodobieństwa:
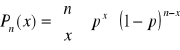
x = 0,1,...,n
dąży dla każdego x = 0,1, do funkcji ![]()
Rozkład zmiennych losowych ciągłych
Rozkład jednostajny (prostokątny, równomierny)
Zmienna losowa ma rozkład jednostajny (na przedziale (a,b)), jeżeli jej gęstość prawdopodobieństwa jest określona wzorem
Dystrybuanta - otrzymujemy ją jako całkę z funkcji gęstości prawdopodobieństwa
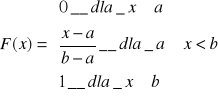
rozkład normalny (Gaussa)
Uznawany za najważniejszy rozkład w teorii prawdopodobieństwa. Gęstość prawdopodobieństwa zmiennej losowej o rozkładzie normalnym:
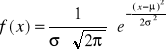
σ > 0
μ - wartość oczekiwana
σ - odchylenie standardowe
N(μ,σ)
rozkład normalny standaryzowany
otrzymywany przez standaryzację zmiennej losowej:
![]()
![]()
![]()
Jeżeli zmienna losowa X ma rozkład normalny N(μ,σ) to zmienna losowa: ![]()
ma rozkład normalny (0,1)
Gęstość prawdopodobieństwa wynosi wówczas:
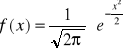
Kształt wykresów:
σ - ma wpływ na kształt wykresu
μ = const
σ4 < σ3 < σ2 < σ1
Odchylenie standardowe jest miara rozrzutu
σ = const
μ1 < μ2 < μ3
Reguła trzech σ
Jeżeli X jest zmienną losową ciągłą o rozkładzie N(μ,σ) to zachodzi: P(μ-3σ ≤ X ≤ μ+3σ) = 0,9973 tzn. takie prawdopodobieństwo, że zmienna losowa przyjmuje takie wartości, które różnią się od wartości oczekiwanej μ nie więcej niż ±3 odchylenia standardowego σ.
rozkład wykładniczy
Zmienna losowa X ma wykładniczy rozkład prawdopodobieństwa, jeśli jej gęstość prawdopodobieństwa wyraża się wzorem
![]()
Parametr λ jest związany z wartością oczekiwaną i wariancją następującymi zależnościami:
![]()
![]()
dystrybuanta
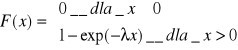
jednym z podstawowych zastosowań rozkładu jest ocena niezawodności różnego rodzaju obiektów technicznych
Funkcja niezawodności R(x) wyraża prawdopodobieństwo zdarzenia losowego polegającego na tym, że czas poprawnej pracy obiektu X nie będzie krótszy, niż pewna wyróżniona wartość x:
R(x)=P(X ≥ x)
Jak łatwo zauważyć:
R(x) = 1-P(X < x) = 1-F(x)
Dlatego, że zdarzenie losowe
X ≥ x i x < x
są zdarzeniami przeciwnymi i tworzą zupełny układ zdarzeń
Jeżeli zmienna losowa X ma wykładniczy rozkład prawdopodobieństwa to funkcja niezawodności ma postać:
R(x) = 1-[1-exp(-λx)] = exp(-λx)
Wykład 3
T: Metoda estymacji przedziałowej
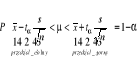
Metoda estymacji przedziałowej to dokonanie szacunku parametru w postaci takiego przedziału (zwanego przedziałem ufności) który z dużym prawdopodobieństwem obejmuje prawdziwą wartość parametru.
W zależności od przyjętych założeń otrzymuje się konkretne wzory na przedziały ufności, w oparciu o rozkład normalny lub rozkład t-studenta
Prawdopodobieństwo
popełnienia błędu wynosi 0,05%
p = 0,025 p = 0,95 p = 0,025
p > 0,9 → metody estymacji
p = 0,95 - 0,99 → w praktyce
Przedział ufności dla średniej
MODEL I
Badana cecha w populacji generalnej ma rozkład normalny N(μ,σ). Wartość średniej μ jest nieznana, odchylenie standardowe σ w populacji jest znane.
W populacji tej pobrano próbę o liczebności n elementów, wylosowanych niezależnie. Przedział ufności dla średniej μ populacji otrzymuje się ze wzoru:
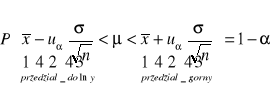
μ - wartość średnia w populacji zawiera się w przedziałach, prawdopodobieństwo wynosi wówczas 1-α ⇒ wartość tą zakłada się w zadaniu
![]()
![]()
- wartość średnia uzyskana z wyników próby
![]()
n - liczebność elementów w próbie
Interpretacja geometryczna
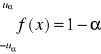
tablice
(1-α) → p |
uα |
0,05 0,01
0,95 0,975 0,99 |
——
——— |
Są dwa typy tablic
wartości uα - na podstawie funkcji gęstości prawdopodobieństwa
wartość uα - na podstawie dystrybuanty
uα - nazywane jest również kwantylem rozkładu
MODEL II
Badana cecha w populacji generalnej ma rozkład normalny N(μ,σ). Nieznana jest zarówno wartość średnia μ, jak i odchylenie standardowe σ w populacji.
Z populacji tej wylosowano niezależnie małą próbę o liczebności n (n<30) elementów. Przedział ufności dla średniej μ populacji otrzymuje się ze wzoru:
gdzie
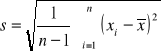
jest odchyleniem standardowym
MODEL III
Badana cecha w populacji generalnej ma rozkład normalny N(μ,σ) bądź dowolny inny rozkład o średniej μ i skończonej wariancji σ2 (nieznanej).
W populacji tej pobrano do próby n niezależnych obserwacji, przy czym liczebność próby jest duża, (co najmniej kilkadziesiąt).Wtedy przedział ufności dla średniej μ populacji wyznacza się ze wzoru jak w modelu I, z tą tylko różnicą, że zamiast σ we wzorze tym używamy wartości odchylenia standardowego s z próby.
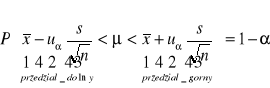
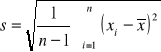
Wykład 4
T: weryfikacja hipotez statystycznych
Jest to drugi obok estymacji, podstawowy rodzaj wnioskowania statystycznego
Dwie grupy hipotez statystycznych
parametryczne, związane z wartościami parametrów
nieparametryczne, związane z postacią rozkładów
Hipoteza statystyczna - to każde przypuszczenie dotyczące wielkości parametru rozkładu zmiennej losowej w populacji generalnej lub próbnej, albo też postaci tego rozkładu, uzyskane na podstawie próby losowej
Testy parametryczne
θ - parametr populacji generalnej
T - przypuszczalna (hipotetyczna) wartość parametru populacji generalnej
H0 - hipoteza zerowa o postaci
H0: θ = T
Co czyta się:
„ Stawiamy hipotezę zerową głoszącą, że wartość parametru θ równa jest T ”
lub
„ Stawiamy hipotezę zerową głoszącą, że pomiędzy parametrem θ a jego oceną T hipoteza jest statystycznie nieistotna (jest na poziomie zerowym)
H1 - hipoteza alternatywna (dla każdej hipotezy zerowej określa się hipotezę alternatywną) o postaciach:
H1: θ ≠ T lub H1: θ > T lub H1: θ < T
Dwie ostatnie hipotezy alternatywne określa się jako hipotezy jednostronne
Podstawową hipotezę zerową weryfikuje się za pomocą odpowiedniego sprawdzianu zwanego testem, który określa się jako zmienną losową o postaci
R0 = θ - T
Wyznaczającą różnicę, dla której następnie buduje się obszar krytyczny odrzuceń hipotezy zerowej na podstawie wartości krytycznej Rα dla danego poziomu istotności α:
R0 = θ - T → test wyznaczamy na podstawie wyników z próby
Rα → wartość określające obszar krytyczny odrzuceń hipotezy zerowej H0, wyznaczana na podstawie poziomu istotności α
H1: θ ≠ T
Jeżeli: ![]()
to hipotezę należy odrzucić
![]()
nie ma podstaw do odrzucenia H0
Testy dla wartości średniej populacji
MODEL I
Badana cecha w populacji generalnej ma rozkład normalny N(μ,σ) przy czym σ jest znane. Na podstawie n-elementowej próby zweryfikować hipotezę zerową:
H0: μ = μ0
μ0 - jest konkretną hipotetyczną wartością średniej, wobec hipotezy alternatywnej (dwustronnie):
H1: μ ≠ μ0
Test dla hipotezy jest następujący:
na podstawie wyników z próby oblicza się:
wartość średnią
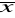
wartość zmiennej standaryzowanej u wg. wzoru
![]()
z
tablic rozkładu normalnego standaryzowanego N(0,1) dla założonego poziomu istotności α wyznacza się wartość krytyczną ![]()
taką by zachodziło ![]()
Obszar krytyczny testu określony jest zależnością
![]()
tzn. że gdy z próby otrzymujemy taką wartość u, ze zachodzi ![]()
to hipotezę zerową H0 odrzucamy.
W przeciwnym przypadku, gdy zachodzi ![]()
nie ma podstaw do odrzucenia H0
POZIOM ISTOTNOŚCI OZNACZENIA PRAWDOPODOBIEŃSTWO
Wartość poziomu istotności określa wartość wystąpienia błędu przy przyjęciu hipotezy zerowej za prawdziwą.
UWAGA
Powyższy test jest testem z dwustronnym obszarem krytycznym i stosuje się go tylko dla dwustronnej hipotezy alternatywnej: H1: μ ≠ 0
Przypadek 1
Hipoteza alternatywna H1 ma postać: H1: μ < μ0
W tym przypadku stosuje się test z lewostronnym obszarem krytycznym. Przy czym wartość uα wyznacza się z tablic z rozkładu normalnego standaryzowanego w taki sposób by była spełniona zależność:
![]()
Hipotezę zerową odrzuca się, jeżeli wyznaczona z próby wartość zmiennej u spełnia nierówność
![]()
Przypadek 2
Hipoteza alternatywna H1 ma postać
W tym przypadku stosuje się test z prawostronnym obszarem krytycznym określony nierównością
![]()
przy czym wartość uα wyznacza się z tablic rozkładu normalnego standaryzowanego w taki sposób by była spełniona zależność:
![]()
hipotezę zerową odrzuca się jeżeli wyznaczona z próby wartość zmiennej u spełnia nierówność
![]()
Testy dla równości średnich dwóch populacji
Testy dla wariancji populacji
Testy dla równości wariancji dwóch populacji
Testy nieparametryczne
Dotyczą postaci rozkładów - tzn. weryfikuje się hipotezy o postaci funkcyjnej rozkładu populacji generalnej
Warunki przeprowadzania:
liczebność próby jest duża
próba jest losowa
poziom istotności nie mniejszy niż 0,01
W celu zweryfikowania hipotezy o postaci rozkładu bada się zgodność rozkładu empirycznego uzyskanego z próby z rozkładem teoretycznym.
χ2 określająca odległość rozkładu empirycznego od hipotetycznego rozkładu teoretycznego
MODEL I
Populacja generalna ma dowolny rozkład o dystrybuancie należącej do pewnego zbioru Ω rozkładów o określonym typie postaci funkcyjnej dystrybuanty. Z populacji tej wylosowano dużą próbę (n>30), której wyniki podzielono na r rozłącznych klas o liczebności ni w każdej klasie, przy czym:
![]()
Otrzymano w tren sposób szereg rozdzielczy
Na podstawie wyników z tej próby należy sprawdzić hipotezę H0, że populacja generalna ma rozkład typu Ω tzn.
H0: F(x)∈Ω
Gdzie F(x) jest dystrybuantą rozkładu populacji
Test zgodności
Wprowadza się charakterystykę, będącą miarą odległości między dystrybuantą rozkładu empirycznego, a dystrybuantą rozkładu hipotetycznego
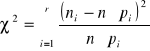
gdzie
ni - liczebność empiryczna i - tego przedziału klasowego (nie powinna być mniejsza niż 10)
r - liczba przedziałów klasowych
pi - prawdopodobieństwo (częstość teoretyczna) odpowiadające wartości badanej cechy w i-tej klasie
![]()
n ⋅ pi - liczebność teoretyczna (oczekiwana) w i-tym przedziale ![]()
Statystyka χ2 ma przy założeniu prawdziwości H0 i przy n → ∞ rozkład χ2 o r stopniach swobody lub o (r - k - 1)stopniach swobody, gdy na podstawie próby oszacowano k parametrów.
Utworzony szereg rozdzielczy jest rozkładem empirycznym
Jako rozkład teoretyczny najczęściej przyjmuje się:
rozkład dwumianowy (Bernouliego)
rozkład Poissona
rozkład normalny
Obliczoną statystykę χ2 należy porównać z wartością krytyczną χα2 odczytaną z tablic rozkładu chi - kwadrat, przy ustalonym poziomie istotności α i określonej liczbie stopni swobody.
Obszar krytyczny w tym teście buduje się prawostronnie, tzn. tak aby była spełniona relacja P (χ2 ≥ χα2 ) = α
Jeżeli zachodzi χ2 ≥ χα2
To H0 należy odrzucić (gdyż różnica między rozkładem empirycznym a hipotetycznym jest statystycznie istotna)
Wykład 5
Planowanie eksperymentu
Informacje wstępne
Planowanie eksperymentu (PE) R. A. Fisher 1935r (w ramach dotyczących analizy wariancyjnej)
Eksperyment - seria doświadczeń, np. w metalurgii seria wytopów stali o różnych składach chemicznych
Cel planowania eksperymentu - wyznaczenie opisu matematycznego obiektu badań lub zjawiska, tzw. modelu matematycznego umożliwiającego analizę jego zachowania i ustalenia czynników wpływających na zachowanie obiektu.
Wybór czynników i zmiennych stanu obiektu badań.
Obiekt badań można przedstawić jako czarną skrzynkę:
RYSUNEK
y1, y2, ym - zmienne wejściowe charakteryzujące stan obiektu w zależności od zmiennych wejściowych - nazywane również zmiennymi stanami, z - zmienna przypadkowa o nieokreślonym rozkładzie niekontrolowana (zakłócenia)
Różnica między zwykłym i statystycznym planowaniem eksperymentu
Wg metody planowania zwykłego zmienne zmienia się stopniowo, przy czym wszystkie pozostałe zmienne utrzymuje się stałe. Następnie zmienia się kolejną zmienną a pozostałe utrzymuje się stałe itd.
Otrzymuje się w ten sposób wyniki badań jako zależności zmiennej stanu od każdej zmiennej przy ustalonym poziomie wszystkich pozostałych zmiennych (np. w postaci krzywej). Potrzebna liczba badań jest duża.
W statystycznym planowaniu eksperymentu dokonuje się zmiany (wariuje się) jednocześnie wszystkich zmiennych w planie eksperymentu.
Eksperyment czynnikowy
Plany rzędu pierwszego
Przykład:
Obiektem badania jest obiekt materialny - aparatura wytwarzająca pewną ilość produktu y. Ilość wyprodukowanego produktu zależy od temperatury x1 i ciśnienia x2 panujących w aparacie.
Oznaczamy maksymalne i minimalne wartości czynników x1 i x2 przez +1 i -1. Wówczas wszystkie możliwe kombinacje czynników przy wariowaniu na dwóch poziomach (max i min) będą określone w czterech doświadczeniach. Taki plan eksperymentu przyjęto zapisywać w postaci macierzy planowania:
Dośw nr |
x1 |
x2 |
y |
1 |
+1 |
+1 |
y1 |
2 |
-1 |
+1 |
y2 |
3 |
+1 |
-1 |
y3 |
4 |
-1 |
-1 |
y4 |
Posługując się taką tablicą (macierzą planowania) można po przeprowadzeniu eksperymentu, wyznaczyć współczynniki równania regresji:
y = b0 + b1x1 + b2x2
W tym przypadku mamy:
Liczba poziomów - 2
Liczba czynników k = 2
Liczba doświadczeń w eksperymencie N = 2k = 22 = 4
Budowa macierzy planowania
Plan eksperymentu zawierający zapis wszystkich kombinacji czynników albo ich części nazywa się macierzą planowania
W budowie macierzy planowania dla dużej liczby czynników stosuje się szereg różnych metod.
Własności macierzy planowania
Macierze planowania posiadają własności związanie z optymalnością modelu, do którego wyznaczenia służą:
1. symetryczność: ![]()
i = 1, 2,..., n - czynniki
2. unormowanie![]()
- ilość doświadczeń
i - numer czynnika
k - numer doświadczenia
Warunek ortogonalności zakłada równość zeru sumy iloczynów elementów dowolnych dwóch kolumn macierzy planowania:
![]()
(i, j = 1, 2,..., n i≠j)
Plan 23
Pełny plan czynnikowy pozwala uwzględnić wzajemne oddziaływania czynników. W tym celu plan eksperymentu uzupełnia się kolumnami, przedstawiającymi iloczyny odpowiednich kolumn czynników.
Dla pełnego eksperymentu czynnikowego 23 macierz planowania eksperymentu z udziałem efektów oddziaływania przedstawia się następująco:
Współczynniki bij oblicza się ze wzoru:
![]()
( i ≠ j )
W te sposób można otrzymać model matematyczny postaci:
![]()
i tak dla planu 23
![]()
N - liczba doświadczeń
n - liczba czynników
Plany rzędu drugiego
Wymaganie adekwatności modelu w obszarze eksperymentu powoduje, że może bardzo często musi on być nieliniowy, np.:
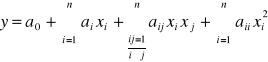
Przy pomocy dotychczas omówionych metod nie da się zbudować takiego modelu, gdyż nie jest spełniony warunek ortogonalności w kolumnach xi2 (suma elementów będzie równa N, a nie 0)
Dla otrzymania modelu o takiej postaci stosuje się plany specjalne
Wybór liczby poziomów
Model matematyczny w postaci wielomianu rzędu drugiego wymaga zastosowania trzech poziomów czynników - 3n
W przypadku liczby czynników większej od 4, pełny eksperyment czynnikowy na 3-ch poziomach jest nieekonomiczny (34 - N = 81, 35 - N = 243)
Plany kompozycyjne
Jeżeli plan PECZ uzupełnimy określonymi (konkretnymi) punktami przestrzeni czynnikowej, można otrzymać plan o mniejszej liczbie doświadczeń niż plan typu 3n
Ogólną liczbę doświadczeń przy takim planowaniu określa się z zależności:
N = 2n + 2n + N0
Gdzie poszczególne składniki określają odpowiednio liczbę doświadczeń w PECZ typu 2n, punktów dodatkowych (tzw. gwiezdnych) i punktów zerowych.
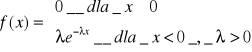
![]()
Wyszukiwarka
Podobne podstrony:
SMiPE - Kolokwium wykład ściąga 2, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperym
Statystyka matematyczna - ściąga 01, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksper
opracowanie pytań na wykład ze statystyki, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie
Statystyka matematyczna - ściąga 02, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksper
Statystyka3, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu, SMiPE
4 Rozklad normalny, STUDIA, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu, SMiPE
01 instrukcja mini, Studia, ZiIP, SEMESTR IV, Statystyka matematyczna i planowanie eksperymentu
Zarzadzanie i systemy jakosci - sciaga I, STUDIA, SEMESTR IV, Podstawy zarządzania, pz, Zarzadzanie,
STATYSTYKA MATEMATYCZNA-sciaga, Automatyka i Robotyka, Semestr IV, Statystyka Matematyczna
Statystyka2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
Statystyka5, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
Statystyka2, ۞ Płyta Studenta Politechniki Śląskiej, Semestr 4, Smipe - Statystyka matematyczna i pl
0 MathCAD, ۞ Płyta Studenta Politechniki Śląskiej, Semestr 4, Smipe - Statystyka matematyczna i plan
statystyka1, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 4, StudiaI
ściąga fizjo, WNOŻCiK (moje studia), Semestr IV, Fizjologia człowieka
Kolokwium wykładowe kinematyka, Studia, Sem 3, III, III Semestr, Mechanika II
więcej podobnych podstron