ćwiczenia 2 - 5 -
Przykład 6
Pionowa winda przemieszcza się z położenia z = 0 w położenie z = 30 m.
Pierwszy odcinek drogi równy h1 = 4 m, winda porusza się ze stałym przyspieszeniem a1, następny odcinek drogi pokonuje ze stałą prędkością V2,
zaś ostatnie trzy metry jest hamowana ze stałym opóźnieniem a3. Należy wyznaczyć wartości liczbowe przyśpieszenia a1, opóźnienia a3 i prędkości V2
ruchu jednostajnego, jeżeli wiadomo, że czas jazdy windy jest równy tC = 6 s
oraz że dla z1 = 0, t = 0, V0 = 0.
Rozwiązanie
z Vk = 0 Warunki brzegowe dla poszczególnych odcinków
1. odcinek h1
h3 z3 t = 0, V = V0 = 0, z1 = 0; t = t1, V = V2, z1 = h1
2. odcinek h2
z2 t = 0, V = V2, a2 = 0, z2 = 0,
h2 t = t2, z2 = h2
V2 = con 3. odcinek h3
a2 = 0 t = 0, V = V2, z3 = 0
h1 z1 t = t3, V = 0, z3 = h3
V0 = 0 rys.6.1 gdzie: z1, z2, z3 współrzędne lokalne
odcinek h1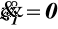
,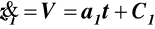
,
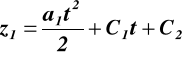
z warunków brzegowych C1 = 0, C2 = 0
równanie ruchu 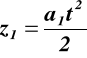
z warunków brzegowych 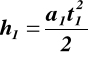
, ![]()
stąd 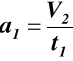
, 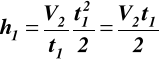
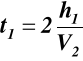
(6.1)
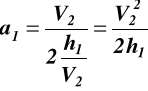
(6.2)
Niewiadome t1 i a1 wyrażone są za pomocą niewiadomej V2
2. odcinek h2 ![]()
, ![]()
, ![]()
z warunków brzegowych C1 = 0
równanie ruchu ![]()
z warunków brzegowych 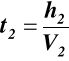
(6.3)
3. odcinek h3 - 6 -
![]()
, ![]()
, 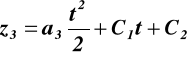
z warunków brzegowych C1 = V2, C2 = 0
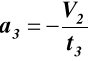
(6.4)
dla z3 = h3 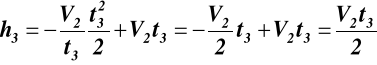
, ![]()
stąd 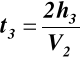
(6.5)
całkowity czas ruchu windy tC = 6 s, dodając (6.1), (6.2), (6.3) otrzymujemy:
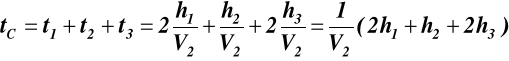
stąd 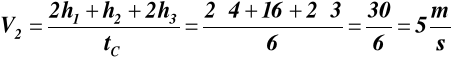
z (6.2) 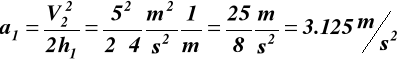
z (6.5) 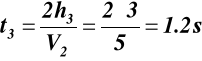
z (6.4) 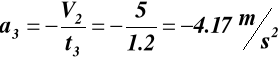
z (6.1) 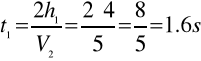
z (6.3) 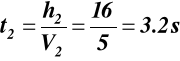
Przykład 7
Punkt poruszając się po linii prostej ze stałym przyśpieszeniem, przebywa kolejno drogi s1 = 2 m, s2 =4 m w czasach t1 = 2 s i t2 = 3 s. Wyznaczyć wartość
liczbową przyśpieszenia a tego punktu.
Rozwiązanie
V0 t1 a t2
s1
s2 Rys.7.1
Równanie ruchu punktu jeśli wektor przyśpieszenia a nie ulega zmianie - 7 -
![]()
, ![]()
, 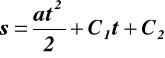
(7.1)
dla t = 0, V = V0 z (7.1) C1 = V0
dla t = 0, s = 0 z (7.1) C2 = 0
stąd 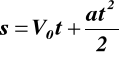
(7.2)
dla t1 = s1 z (7.2) 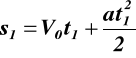
stąd 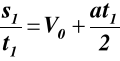
(7.3)
dla t2 = s2 z (7.2) 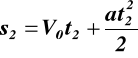
stąd 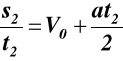
(7.4)
odejmując (7.4) od (7.3) 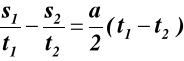
, 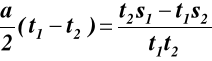
Przykład 8
Do końca A nierozciągliwej liny AC przywiązane zostało ciało, które może ślizgać się po poziomej prowadnicy. Lina AC przerzucona została przez krążek B, który należy traktować jako punkt i jej koniec C ciągnięty jest z prędkością
VC = 3 m/s po poziomej prostej znajdującej się w odległości h = 1.2 m od prowadnicy (rys.8.1). Należy wyznaczyć prędkość punktu A w zależności od współrzędnej s (rys.8.1) oraz dla s = 2 m.
x
x A v B
h
C VC
s
s Rys.8.1
Rozwiązanie
Zgodnie z przyjętym na rysunku zwrotem osi x 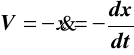
długość liny ![]()
, ![]()
![]()
, (8.1)
- 8 -
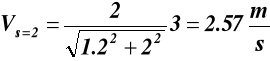
Przykład 9
Na rysunku 9.1 przedstawiony jest schematycznie mechanizm korbowy składający się z wału korbowego OA, który może obracać się wokół osi O, korbowodu AB, oraz tłoka B. Końce korbowodu połączone są przegubowo z wałem korbowym i tłokiem. Należy wyznaczyć prędkość i przyspieszenie tłoka w przypadku gdy wał korbowy obraca się ze stałą prędkością kątową ω czyli że
* = ωt. Długość OA = r, długość AB = l (rys.9.1).
A
r l
* = ωt
0 β VB aB x
B
Rys.9.1
x
Rozwiązanie
![]()
(9.1)
z trójkąta 0AB 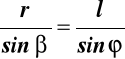
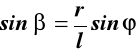
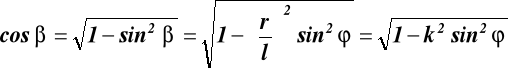
, gdzie 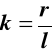
![]()
, ![]()
, 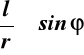
Podstawiając cosβ do (9.1) otrzymujemy:
![]()
(9.2)
różniczkując równania ruchu (9.2) punktu B, otrzymujemy wzór na prędkość
punktu B 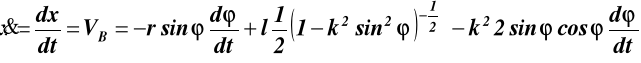
- 9 -
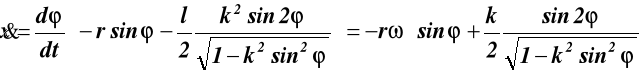
niech k = 0.1 wtedy ![]()
czyli jeśli k << 1 to 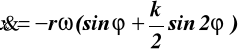
(9.3)
dla takiego przypadku, przyśpieszenie obliczamy różniczkując równanie (9.3)
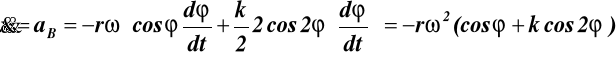
dla l = 20cm, r = 2cm, k = 0.1
dla * = 0, π, 2π, 3π.... VB = 0
dla * = 0, aB = -rω2(1+k) = -1.01 rω2
dla * = π, aB = rω2(1- k) = 0.99rω2
Przykład 10
Punkt A porusza się wzdłuż osi x z przyśpieszeniem a (rys.10.1), którego wartość a jest proporcjonalna do odległości wspomnianego punktu od nieruchomego punktu 0 leżącego na tej osi. Wyznaczyć równanie ruchu
punktu A.
V0 ax
0 A0 A x
x0
x Rys.10.1
Rozwiązanie
![]()
niech ![]()
wtedy ![]()
, ![]()
(10.1)
rozwiązaniem równania (10.1) jest równanie ruchu punktu A wzór (10.2)
![]()
(10.2)
równanie prędkości ![]()
(10.3)
jeśli dla t = 0: 1) x = x0
2) V = V0
to z warunku 1) x0 = D1 + D2 (10.4)
z warunku 2) ![]()
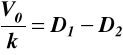
(10.5)
z sumy (10.4) i (10.5) mamy: 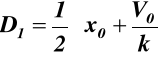
(10.6)
- 10 -
z różnicy (10.4) i (10.5) mamy: 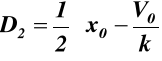
(10.7)
podstawiając D1 i D2 do (10.2) i do (10.5) otrzymujemy wzory na równanie:
ruchu punktu 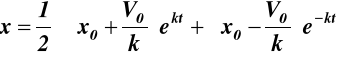
prędkości 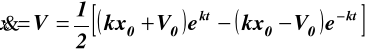
Wyszukiwarka
Podobne podstrony:
Mechanika - Kinematyka, cwiczeniakinematyka3, Ćwiczenia 3
Mechanika - Kinematyka, cwiczeniakinematyka4
Mechanika - Kinematyka, cwiczeniakinematyka5, Ćwiczenie 5
Mechanika gruntów Ćwiczenie 5 Sprawozdanie 3
Mechanika gruntów - Ćwiczenie 1 - Sprawozdanie 1, Budownictwo S1, Semestr III, Mechanika gruntów, La
Mechanika gruntów - Ćwiczenie 5 - Sprawozdanie 4, Budownictwo S1, Semestr III, Mechanika gruntów, La
podst mechaniki plynow cwiczenia
Symulacja E ogarnijtemat.com, SiMR inżynierskie, Semestr 4, Laboratorium Mechaniki Płynów, Ćwiczenia
sprawko przeplyw nasze ogarnijtemat.com, SiMR inżynierskie, Semestr 4, Laboratorium Mechaniki Płynów
Mechanika - Dynamika, cwiczeniadynamika12, Cwiczeniadynamika11
mechanika, 14+, Ćwiczenie 15
Mechanika gruntów Ćwiczenie 1 Sprawozdanie 2
Mechanika płynów ćwiczenia
Mechanika gruntów Ćwiczenie 4 Sprawozdanie
Mechanika - Statyka, cwiczeniastatyka3, Ćwiczenia statyka 3
więcej podobnych podstron