Metody numeryczne

Materiały dydaktyczne dla studentów

dr inż. Radosław Łuczak

Koszalin - Słupsk 2008

Spis treści

Wykorzystane oznaczenia i skróty

Wstęp

1. Algorytmy i struktury danych

a) elementy schematów blokowych

c) przykładowe algorytmy i implementacja w C++

d) rekurencja, rekursja

e) zadania dla studentów

2. Błędy obliczeń

a) reprezentacja liczb w pamięci komputera

b) typy danych w C++

c) operacje na zmiennych

c) Błąd zaokrągleń - powstawanie

d) wyliczanie wartości funkcji złożonych - rozwinięcia w szereg

e) przykłady rozwinięcia niektórych funkcji

f) Schemat Hornera - redukcja operacji zmiennoprzecinkowych

f) Błąd obcięcia

g) zadania dla studentów

3. Numeryczne rozwiązywanie równań nieliniowych

a) Pochodna funkcji, rozwinięcie w szereg Taylora

b) Metoda punktu stałego

c) Metoda bisekcji

d) Metoda siecznych

e) Metoda stycznych (Newtona-Raphsona)

f) Warunki zbieżności procesu iteracyjnego, strategia wyboru punktu startowego

f) zadania

4. Całkowanie numeryczne

a) Funkcja pierwotna, interpretacja geometryczna całki

b) Przykłady analitycznego obliczenia wybranych całek oznaczonych

c) Metoda prostokątów i metoda trapezów

d) Metody interpolacyjne i ekstrapolacyjne, porównanie interpolacyjnego i ekstrapolacyjnego algorytmu Eulera.

e) Algorytmy Adamsa-Moultona

f) Algorytmy Adamsa-Bashfortha

g) Algorytmy Geara

h) Porównanie dokładności metod całkowania numerycznego

i) Stabilność algorytmów całkowania numerycznego

i) zadania dla studentów

5. Układy równań liniowych

a) Operacje na macierzach - rachunek macierzowy

b) Wyznacznik macierzy

c) Uwarunkowanie macierzy

f) backward substitution, forward substitution - algorytmy redukcji wstecznej i w przód

d) Metoda eliminacji Gaussa-Jordana

e) Metoda Eliminacji Gaussa

f) Metoda LLT

g) Rozkład LU, metoda Crouta

g) Strategia wyboru elementu głównego

h) zadania dla studentów

6. Aproksymacja

a) Zadanie najmniejszych kwadratów

b) Interpolacja wielomianem Lagrange'a

e) Interpolacja technikami numerycznymi

f) macierz funkcji bazowych

g) aproksymacja metodą najmniejszych kwadratów

h) Ekstrapolacja

i) zadania dla studentów

7. Zakończenie

8. Bibliografia

1. Algorytmy i struktury danych

Niniejszy rozdział ma charakter wstępny. Znalazły się w nim wybrane informacje znane studentom z poprzednich lat nauki, z takich przedmiotów jak „teoretyczne podstawy informatyki” czy „algorytmy i struktury danych”. Uznano jednak za wskazane przypomnienie tych wiadomości ze względu na częste odwołania do pojęć występujących w tym rozdziale. Zamieszczono zatem pewne definicje, określenia oraz przybliżono niektóre problemy ilustrując je przykładami.

1.1. Definicja algorytmu, język algorytmu

Algorytm - skończony, uporządkowany ciąg jasno zdefiniowanych czynności, koniecznych do wykonania pewnego zadania.

Algorytm ma przeprowadzić system z pewnego stanu początkowego do pożądanego stanu końcowego. Badaniem algorytmów zajmuje się algorytmika.

Słowo „algorytm” pochodzi od nazwiska matematyka perskiego z IX wieku Muhammed ibn Musa Alchwarizmi (أبو عبد الله محمد بن موسى الخوارزمي) i początkowo oznaczało w Europie sposób obliczeń oparty na dziesiętnym systemie liczbowym.

Algorytmy można przedstawiać w najróżniejszy sposób. Chociaż powszechnie przyjęto formę graficzną tzw. schemat blokowy (SB), to każda inna forma, w świetle definicji, np. opis słowny kolejno (sekwencyjnie) wykonywanych czynności, także jest algorytmem [B1, B2].

Algorytm jest uniwersalnym przepisem, niezależnym od języka programowania, stąd występują w nim operacje o charakterze uniwersalnym, zrozumiałym dla każdego programisty. Dopiero implementacja algorytmu w postaci programu komputerowego napisanego w konkre­tnym języku, wymaga stosowania właściwych dla niego operacji (rozdział 1.3.).

Na przykład instrukcję przypisania, która zmiennej a nadaje określoną wartość (np. 2) w sche­matach blokowych zapisuje się jako:

(1.1)

W implementacjach, zależnie od języka, instrukcja ta może być zapisana w postaci:

(w języku C) (1.2)

(w języku Pascal) (1.3)

Programista nie znający Pascala, ale C, mógłby opatrznie rozumieć instrukcję (1.3). W języku C można bowiem zapisywać operacje arytmetyczne w sposób uproszczony, np.:

(1.4)

co jest równoważne do instrukcji

(1.5)

Instrukcja (1.3) może zatem zostać zinterpretowana jako dzielenie przez 2. Z kolei instrukcja (1.2) wygląda jak typowe Pascalowe porównanie i dla osób znających ten język programowania algorytm byłby nieczytelny.

Ten prosty przykład dowodzi konieczności przyjęcia uniwersalnego sposobu zapisu. Czytelna dla wszystkich instrukcja przypisania, wykorzystana w algorytmie, ma postać (1.1).

W niniejszej pracy, ze względu na implementację jedynie w C++, zaniechano jednak tej zasady i instrukcję przypisania oznacza się na schematach tak jak w języku C++ (1.2).

1.2. Elementy schematów blokowych

Do tworzenia schematów blokowych wykorzystuje się zaledwie kilku elementów. Wszystkie zostały przedstawione i krótko opisane.

Początek i koniec działania algorytmu.		Instrukcje wejścia/wyjścia. Wprowadzanie danych i wyświetlanie (drukowanie) wyników.
Ścieżki wyznaczające kolejność wykonywanych instrukcji.		Instrukcja przypisania. Wyniki wszelkich obli­czeń przepisywane są do zmie­nnej, obliczenia realizuje się w instrukcji przypisania.
Instrukcja warunkowa. Warunek spełnionu: wybór drogi T (tak). Warunek niespełniony: wybór drogi N (nie).		Łączniki. Jeżeli część schematu rysowana jest w innym miejscu, to rozerwane ścieżki nume­ruje się zaznaczając rozcięcia okręgiem.
Instrukcje złożone, zawierające wiele instrukcji elementarnych. W tym przypadku algorytm Euklidesa.

1.3. Przykładowe algorytmy i ich implementacja w języku C++

W niniejszym rozdziale znalazło się kilka wybranych algorytmów wraz z implemantacją w języku C++. Przykłady te mają ilustrować i wyjaśniać pewne problemy pojawiające się przy próbie zapisania instrukcji podanych w algorytmie (schemacie blokowym) w konkretnym języku programowania. Dodatkowo podnosi się temat efektywności algorytmów.

1.3.1. Algorytm Euklidesa.

Algorytm pozwala na znajdowanie największego dzielnika liczb. Wbrew przypuszczeniom nie został on jednak wymyślony przez Euklidesa, który jedynie zamieścił go w swoich „Elementach geometrii”, które systematyzowały ówczesną wiedzę z matematyki.

Rys. 1.1. Algorytm Euklidesa

#include <stdio.h> #include <conio.h> int a,b,r; int main() { printf("Podaj A="); scanf("%d",&a); printf("Podaj B="); scanf("%d",&b); printf("NWD liczb %d i %d wynosi ",a,b); ———————————————————————————————— r=a%b; while (r) { a=b; b=r; r=a%b; } printf("%d",b); ————————————————————————————————— do { r=a%b; a=b; b=r; } while (r) printf("%d",a); ———————————————————————————————— getch(); return 0; }

Pomimo pozornej prostoty „oprogramowanie” tego algorytmu może stanowić pewną trudność. Należy zauważyć, że wystąpiła w nim pętla z warunkiem w środku.

W typowym przypadku, we wszystkich językach programowania, występują dwa rodzaje instrukcji iteracyjnych z warunkowym zakończeniem. W języku C++ są to while () {…} i do {…} while (). Odpowiednie algorytmy ilustrujące działanie tych instrukcji przedstawiono na rys. 1.2.

Rys. 1.2. Schematy blokowe instrukcji iteracyjnych: while () {…}, do {…} while ().

Zauważmy, że w algorytmie Euklidesa (rys. 1.1.) nie występuje blok o strukturze takiej jak na rys. 1.2. Czy to oznacza, że nie można zrealizować go programowo? Oczywiście można, ale niestety nie wprost.

Rozdzielone w algorytmie bloki operacyjne [R=A mod B] oraz [A=B, B=R] zostaną połączone i umieszczone w bloku [instrukcja] na jednym z algo­rytmów z rys. 1.2. Pociągnie to za sobą konkretną zmianę algorytmu z rys. 1.1. Zastosowanie instrukcji while () {…} spowoduje wystąpienie dodatkowego obliczania reszty z dzielenia (r=a%b) przed wejściem do pętli, zastosowanie do {…} while () — nadmiarowe przypisania w ostatnim kroku iteracji (a=b; b=r;).

Program z zastosowaniem obu instrukcji przedstawiono obok algorytmu, wydzielając odpowiednie fragmenty.

Proces zapisania algorytmu w konkretnym języku programowania, w którym są do dyspozycji właściwe dla niego instrukcje powodujące czasem konieczność adaptacji (zmiany) algorytmu nazywa się implementacją.

1.3.2. Ciąg Fibonacciego

Leonardo z Pizy zwany Fibonaccim (Leonardo Pisano, Filius Bonacci) włoski matematyk, zasłużył się nauce europejskiej wprowadzając do użytku (cyfry) liczby arabskie. Jednakże współcześnie Fibonacci kojarzy się z ciągiem podanym przez niego w 1202 roku. jest to ciąg liczb naturalnych, w którym pierwsze dwie są równe 1, a każda kolejna jest sumą 2 poprzednich. Od Fibonacciego wzięła swoją nazwę także liczba  - „złota liczba” którą kojarzy się ze „złotym podziałem odcinka”.

W niniejszej części przedstawiony zostanie algorytm wyliczania k-tego elementu ciągu Fibonacciego oraz kilka ciekawostek związanych z tym ciągiem i liczbą .

Algorytm wraz z implementacją przedstawia rysunek 1.4. Należy podkreślić, że w odróżnieniu od poprzedniego przykładu, w którym mowa była o instrukcjach while () {…}, do {…} while (), algorytm zawiera pętlę (instrukcję iteracyjną) o znanej z góry liczbie wykonywanych kroków. Specjalnie dla takich sytuacji stworzona została instrukcja for (…) i wraz z omawianymi wcześniej, tworzy komplet instrukcji iteracyjnych w większości języków programowania. Schemat blokowy dla instrukcji for (…) przedstawiono na rysunku 1.3. Charakterystyczną cechą instrukcji for (…) jest występowanie zmiennej (tutaj i), której zadaniem jest przede wszystkim określenie, czy należy już zakończyć iteracje. Zmienna ta jest w każdym kroku zwiększana aż do osiągnięcia wymaganej wartości (i=K).

	for (i=1; i<k; i++) { instrukcja realizowana w pętli for() }
Rys. 1.3. Schemat blokowy instrukcji for (…) {…}, przykład w języku C++.

Kolejne wartości ciągu Fibonacciego.
k	1	2	3	4	5	6	7	8	9		10	11	12	13	14	15	16
Fib	1	1	2	3	5	8	13	21	34		55	89	144	233	377	610	987
										#include <stdio.h> #include <conio.h> int a,ak,s,i,k; int main() { printf("Podaj K="); scanf("%d",&k); ak=1; if (k>2) { a=1; for (i=2;i<k;i++) { s=a+ak; a=ak; ak=s; } } printf("Fib[%d]=%d",k,ak); getch(); return 0; }
Rys. 1.4. Schemat blokowy algorytmu wyliczającego k-ty element ciągu Fibonacciego z implementacją.

Własności ciągu Fibonacciego

1. Największy wspólny dzielnik dwóch dowolnych liczb Fibonacciego jest liczbą Fibonacciego, której numer jest równy najmniejszemu wspólnemu dzielnikowi tych liczb.

2. Jedynymi liczbami w całym ciągu Fibonacciego, będącymi kwadratami liczb całkowitych są 1 i 144.

3. Każda niezerowa liczba całkowita ma wielokrotność będącą liczbą Fibonacciego.

4. Iloraz dwóch kolejnych liczb Fibonacciego przybliża liczbę .

Rys. 1.5. Kwadraty Fibonacciego. Ciąg kwadratów, których długości boków są liczbami Fibonacciego.

Liczba  jest współczynnikiem właściwych proporcji (patrz zadanie 1.4.). Definiowana jest jako granica:

(1.6)

ale można ją także wyliczyć analitycznie, gdyż jako jedyna spełnia równanie

(1.7)

Równanie to rozwiązane zostanie w dalszej części książki metodami numerycznymi.

1.3.3. Sortowanie metodą zamiany prostej

Zadanie polega na ułożeniu elementów zbioru we właściwej kolejności, zgodnie z przyjętym kryterium. W programach najczęściej sortuje się n wartości umieszczonych w zmiennej tablicowej.

				i ▼			j ▼
indeks	0	1	2	3	4	5	6	7	8	9	10
wartość	12	17	28	38	71	97	31	43	52	69	61
	już posortowane			jeszcze nie posortowane

Sortowanie metodą zamiany prostej odbywa się przez porównywanie wartości o indeksie i (w komórce i) z wartością o indeksie j, przy czym i∈<0..n-1>, a j∈<i+1..n>. Jeżeli wartość w komórce j jest mniejsza od wartości w komórce i, wówczas wartości się zamienia.

#include <conio.h> #include <stdio.h> #include <stdlib.h> const int n=10; int i,j,m; int a[n]; int main() { for (i=0;i<=n;i++) { a[i]=10+rand()%90; // losowanie i wyświetlanie // wartości nieposortowanych printf("%3d",a[i]); } printf("\r\n"); for (i=0;i<n;i++) // sortowanie { for (j=i+1;j<=n;j++) if (a[j]<a[i]) { m=a[i]; a[i]=a[j]; a[j]=m; } printf("%3d",a[i]); // wyświetlanie posortowa- //nych wartości } printf("%3d",a[n]); getch(); return 0; }

Rys. 1.5. Schemat blokowy i implementacja sortowania przez zamianę prostą.

W wyniku działania programu na ekranie ukazuje się nieposortowany ciąg liczb a pod nim wyświetlane są liczby w kolejności rosnącej.

Sortowanie przez zamianę prostą jest mało efektywne. Program dokonuje n²/2 porównań, a w wyniku każdego porównania może dojść do wymiany wartości w komórkach i i j.

Mówiąc inaczej, w komórce o indeksie i powinna być umieszczona najmniejsza wartość z zakresu <i..n>. Program realizuje to poprzez wprowadzenie zmiennej indeksowej j∈<i+1..n> i porówny­wanie oraz szereg zamian, gdzie każda z nich zmienia wartość w komórce i. Dopiero po ostatniej zamianie w komórce i znajduje się najmniejsza wartość z zakresu <i..n>.

Wynika z tego, że wszystkie zamiany z wyjątkiem ostatniej były wykonywane niepotrze­bnie i powodowały jedynie wzrost złożoności numerycznej.

1.3.4. Sortowanie przez wybieranie

Odmianą techniki sortowania przez zamianę prostą jest sortowanie przez wybieranie. Jej efektywność jest znacznie większa ponieważ liczba zamian jest ograniczona do n-1, co w porównaniu z n²/2 z poprzedniego przykładu daje znaczną redukcję złożoności numerycznej.

	#include <conio.h> #include <stdio.h> #include <stdlib.h> const int n=10; int i,j,idm,mem; int a[n]; int main () { for (i=0;i<=n;i++) { a[i]=10+rand()%90; // losowanie i wyświetlanie wartości nieposortowanych printf("%3d",a[i]); } printf("\r\n"); for (i=0;i<n;i++) // sortowanie przez wybieranie { idm=i; for (j=i+1;j<=n;j++) if (a[j]<a[idm]) idm=j; if (idm>i) { mem=a[i]; a[i]=a[idm]; a[idm]=mem; } printf("%3d",a[i]); // wyświetlanie posortowanych wartości } printf("%3d",a[n]); getch(); return 0; }

Różnica polega na zaniechaniu zamian w pętli wewnętrznej. Instrukcja

	idm=i; for (j=i+1;j<=n;j++) if (a[j]<a[idm]) idm=j;

Dokonuje tylko przepisania wartości i do zmiennej idm której zadaniem jest wskazanie najmniejszej wartości z zakresu <i..n>. Odszukanie mniejszej wartości w wyniku przeglądania tablicy (zwiększania j) nie wywołuje zamiany a jedynie przepisanie wartości j do idm.

Na końcu pętli w zmiennej idmznajduje się indeks najmniejszej wartości z zakresu <i..n>. Dopiero teraz program dokonuje właściwej wymiany w komórkach tablicy.

1.4. Rekurencja - rekursja

Przedstawiony opisowo w rozdziale 1.3.2. wzór na k-ty element ciągu Fibonacciego można zapisać formalnie w postaci:

(1.8)

Takie przedstawienie wzoru wartości k-tego elementu, do obliczenia której potrzebna jest znajomość wszystkich poprzednich wyrazów nazywa się opisem rekursywnym.

Z opisem rekursywnym spotykamy się stosunkowo często np.:

(1.9)

Ze wzoru (1.9) wylicza się wartość k-silnia.

Około 1740 roku Euler, a 100 lat po nim w 1843 J. Binet podali inny wzór na obliczenie k-tego wyrazu ciągu Fibonacciego.

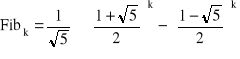
(1.10)

Ze wzoru Eulera-Bineta wylicza się wartość bezpośrednio, nie jest konieczna znajomość wartości wyrazów poprzedzających k. Zatem (1.10) jest wzorem bezpośrednim - analitycznym.

W niektórych przypadkach wykorzystanie wzorów analitycznych może być kłopotliwe lub wręcz niemożliwe. Porównajmy wzór (1.10) ze wzorem (1.8). Wyrażenie (1.8) jest bardzo proste natomiast (1.10) jest skomplikowane, występuje k-ta potęga liczby niewymiernej. Wynikiem wyrażenia (1.10) jest zawsze liczba naturalna, ale komputer wyliczałby liczbę rzeczywistą. Na skutek konieczności użycia zmiennych rzeczywistych (float) oraz ze względu na występujące błędy zaokrągleń. Wynik nigdy nie będzie liczbą naturalną.

Do obliczenia F_k ze wzoru (1.8) czy k! z (1.9) można zastosować wywołanie rekurencyjne.

Przykład

k-ty element ciągu Fibonacciego

	int fib(int k) { int f; if (k<=1) f=1; else f=fib(k-1)+fib(k-2); return f; }

k-silnia

	int silnia(int k) { int s; if (k<1) s=1; else s=k*silnia(k-1); return s; }

Zdefiniowano funkcje, które wywołują same siebie. Jest to wywołanie rekurencyjne. W przykładzie przedstawiono rekurencję pierwszego rodzaju czyli funkcja A wywołuje funkcję A. Istnieje rekurencja drugiego rodzaju polegająca na zapisaniu funkcji A i B w taki sposób, że funkcja A odwołuje się do B, a B odwołuje się do A.

Na zakończenie rozważań o rekurencji przyjrzyjmy się przedstawionym przykładom. W funkcji silnia() następuje jednokrotne wywołanie funkcji silnia(). Jest to bardzo eleganckie wywołanie, nie powodujące zbędnych obliczeń. Zupełnie inaczej wygląda funkcja fib() która wywołuje się dwukrotnie. Każde z tych wywołań znów dwukrotnie odwołuje się do funkcji fib(). Ilość wywołań funkcji narasta lawinowo. Obliczenie np.: 15-go wyrazu ciągu wymaga obliczenia wyrazu pierwszego 2¹⁵ razy, drugiego 2¹⁴ razy itd.

To z pozoru drobna niedogodność. Jednakże liczba wywołań funkcji fib() będzie proporcjonalna do wartości 2^k. Oznacza to, że nawet dla niewielkich wartości k (rzędu 100), żaden komputer na świecie nie poradzi sobie z zakończeniem obliczeń, niezależnie od tego jak jest szybki i niezależnie od czasu trwania obliczeń. Już dla k=44 czas obliczeń wynosi około 30s. W tym przypadku zastosowanie odwołania rekurencyjnego jest nieefektywne. Należy raczej wykorzystać program umieszczony obok rys. 1.4. Istnieją jednak problemy, dla których znalezienie nierekurencyjnego rozwiązania nie jest proste a nawet niepotrzebne ze względu na elegancję i efektywność rekurencji w tych przypadkach.

1. 5. Zadania dla studentów

1.1. Stosując algorytm Euklidesa wylicz najmniejszą wspólną wielokrotność liczb.

1.2. Zapisz algorytm Euklidesa w funkcji int NWD(int a, int b) i wykorzystaj do znalezienia największego dzielnika i najmniejszej wielokrotności N liczb podanych z klawiatury.

1.3. Zapisz algorytm 1.3. w postaci funkcji i oblicz iloraz F_k/F_k-1 dla N kolejnych liczb Fibonacciego.

1.4. Podziel odcinek na części A i B w taki sposób, aby stosunek A/B=(A+B)/A, jaka jest wartość tego stosunku (oblicz). Porównaj z ilorazami z poprzedniego zadania.

1.5. Zapisz wzór (1.10) w postaci funkcji liczby .

1.6. Narysuj schemat blokowy realizujący sortowanie przez wybieranie.

1.7. Określ doświadczalnie, ile razy szybciej działa metoda sortowania przez wybieranie od sortowania met. zamiany prostej.

1.8. Napisz program obliczający i wyświetlający na ekranie kolejne wartości k! Kiedy następuje przepełnienie?

2. Błędy obliczeń

Obliczenia prowadzone przy użyciu komputera zawsze obarczone są błędami. Wynika to z kilku specyficznych cech związanych z budową komputera, przechowywaniem danych w pamięci operacyjnej (w zmiennych) oraz sposobem realizacji operacji arytmetycznych.

Mikroprocesor potrafi wykonywać jedynie kilka elementarnych operacji na liczbach całkowitych, binarnych: dodawanie i odejmowanie oraz przesunięcie w lewo i w prawo. Operacje przesunięcia w lewo i w prawo wykonane na liczbach systemu dwójkowego (binarnych) odpowiadają mnożeniu i dzieleniu przez 2.

Inne operacje arytmetyczne, takie jak mnożenie i dzielenie dowolnych liczb wymagają algorytmu, który będzie je wykonywał bazując na operacjach elementarnych.

Dodatkowo, wykonywanie operacji na liczbach zmiennoprzecinkowych wymaga przyjęcia umowy, w jaki sposób skończony ciąg bitów, zapisanych w pamięci komputera, będzie reprezentował liczbę rzeczywistą. Przestrzeń przeznaczona na zapisanie liczby rzeczywistej jest skończona, natomiast liczba może mieć nieskończenie wiele miejsc po przecinku (niewymierna). Z tego względu liczba zapisana w zmiennej ma zawsze skończoną precyzję. Zapis liczby w zmiennej (zaledwie w kilku bajtach) obarczony jest błędem.

Jest to pierwszy powód ograniczonej dokładności obliczeń - skończony obszar przeznaczony do zapisania liczby zmiennopozycyjnej. Wynikiem tej skończonej precyzji jest tzw. błąd zaokrągleń, który jest skutkiem porzucenia (zaokrąglenia) liczby tylko do kilku miejsc po przecinku.

Drugim z pojawiających się błędów jest błąd obcięcia. Oba zostaną omówione w dalszej części rozdziału.

2.1. Reprezentacja liczb w pamięci komputera

Aby dobrze zrozumieć mechanizm błędu zaokrągleń należy poznać sposób zapisu liczb w pamięci komputera.

2.1.1. Liczby stałopozycyjne

W praktyce reprezentację stałopozycyjną stosuje się jedynie dla liczb całkowitych. Istnieją 2 rodzaje reprezentacji liczb całkowitych: ze znakiem i bez znaku.

Liczba całkowita dwubajtowa, zapisana w pamięci ma postać

binarnie	1	0	0	1	1	0	1	1		0	1	0	1	1	1	0	1
szesnastkowo	9				B					5				D
dziesiętnie	155									93

Za pomocą 2 bajtów można zapisać liczbę z przedziału <0 ... 65535> bez znaku (unisigned int), lub <-32768...32767> ze znakiem (int).

Przedstawiony w tabeli ciąg bitów reprezentuje liczbę 155·256+93=39773 lub 39773-32768=7005 w zależności czy jest to zmienna typu unsigned int, czy int.

Analogicznie interpretowane są jednobajtowe czy czterobajtowe liczby całkowite.

Omawiając zapis liczb stałopozycyjnych pominięto kolejność bajtów. W praktyce najstarszy bajt stoi po prawej stronie.

2.1.2. Liczby zmiennopozycyjne

Zapis liczb zmiennopozycyjnych jest określony w standardzie IEEE 754.

Liczby zapisywane są w pamięci komputera w postaci ciągu bitów, który interpretowany jest jako liczba o postaci L=Zn·Ma·2^Ce.

gdzie:

Zn - znak, Ma - mantysa, Ce - cecha.

Znak zapisywany jest w pierwszym bicie: 0-liczba dodatnia; 1-liczba ujemna. Cecha jest liczbą całkowitą z przesunięciem. Mantysa jest znormalizowana 1<Ma<10, czyli przecinek stoi po pierwszej niezerowej cyfrze.

Liczbę 15,24 po znormalizowaniu (w systemie dziesiętnym) zapisuje się 1,524·10¹.

Binarnie ta sama liczba zapisywana jest 1111,00111101 - po znormalizowaniu 1,11100111101·2¹¹.

Pierwszy bit mantysy jest zawsze równy 1, zatem nie jest zapisywany.

precyzja	znak	przesunięta cecha	mantysa (część ułamkowa)	przesunięcie
		ile bitów [które]	ile bitów [które]		ile bitów [które]
pojedyncza (4B)	1 [31]	8 [30-23]	23 [22-0]	127
podwójna (8B)	1 [63]	11 [62-52]	52 [51-0]	1023

Przykład

Liczbę 23,75 zapiszemy zgodnie z IEEE 754 - pojedyncza precyzja.

Zamieniamy ją na postać binarną: 10111,11.

Po znormalizowaniu 1,011111·2¹⁰⁰.

znak: 0

wykładnik: 4 + 127 = 131, binarnie 10000011

część ułamkowa: 011111 (pomijamy bit przed przecinkiem)

Uzyskuje się:

znak	przesunięta cecha (8 bitów)	część ułamkowa (23 bity)
0	1 0 0 0 0 0 1 1	0 1 1 1 1 1 00000000000000000

Na szaro zaznaczono uzupełnione zera do 23 bitów.

Ostatecznie mamy 01000001 10111110 00000000 00000000, co daje szesnastkowo 41 BE 00 00.

Liczba 23,75 nie została zaokrąglona. Zapisując ją zgodnie z normą nie popełnia się błędu.

Ponówmy operację dla liczby -11,71.

Postać binarna: 1011,1011010111000010100011101111(…) (ograniczono do 30 miejsc po przecinku)

Po znormalizowaniu: 1,0111011010111000010100011101111(…)·2¹¹

znak: 1

wykładnik: 3 + 127 = 130, binarnie 10000010

część ułamkowa: 01110110101110000101000 11101111 (na szaro oznaczono bity odrzucone)

Uzyskuje się:

znak	przesunięta cecha (8 bitów)	część ułamkowa (23 bity)
1	1 0 0 0 0 0 1 0	01110110101110000101000

Ostatecznie 11000001 00111011 01011100 00101000, co daje szesnastkowo C1 3B 5C 28.

Liczba -11,71 została zaokrąglona w dół. Zapisując ją popełnia się błąd.

Przykład

Program przelicza liczbę z zakresu (0…1) zapisaną dziesiętnie w a na postać binarną (n bitów).

	#include <stdio.h> #include <conio.h> const int n=30; float a=0.24, mn=1; int i; int main() { for (i=1;i<=n;i++) { mn=mn*0.5; if (mn<a) { printf("1"); a=a-mn; } else printf("0"); } getch(); return 0; }

2.2. Typy danych w C++

W niniejszym rozdziale przedstawiono typy danych dostępne w języku C++. Zaznaczono rozmiar zmiennej i pokazano zakresy wartości jakie może przyjmować.

Nazwa	Wielkość		Zakres wartości zmiennej			Precyzja zmiennej
		bity	bajty	min	…	max	po przecinku
liczbowe, całkowite
unsigned char	8	1	0	…	255	—
char	8	1	-128	…	127	—
enum	16	2	-32,768	…	32,767	—
unsigned int	16	2	0	…	65,535	—
int	16	2	-32,768	…	32,767	—
short int	16	2	-32,768	…	32,767	—
unsigned long	32	4	0	…	4,294,967,295	—
long	32	4	-2,147,483,648	…	2,147,483,647	—
liczbowe, rzeczywiste
float	32	4	±1,5·10^-^45	…	±3,4·10^38	7 - 8
double	64	8	±5,0·10^-3^24	…	±1,7·10^3^0^8	15 - 16
long double	80	10	±3,4·10^-^49^3^2	…	±1,1·10^4932	19 - 20

Zawarte w tabeli informacje dotyczą kompilatora Borland C ver. 3.1 for DOS.

2.3. Błąd zaokrągleń

W rozdziale 2.1.2. przedstawiono zapis liczb zmiennopozycyjnych i wspomniano o błędach. Były to błędy zaokrągleń, z tym, że operowano na liczbach systemu binarnego. W niniejszym rozdziale będziemy omawiać błędy zaokrągleń i ich skutki, ale na liczbach przekształconych ponownie do 10-nego systemu liczenia.

Błąd zaokrąglenia pojawia się przy próbie zapisania w zmiennej takiej wartości, która ma więcej miejsc po przecinku (po znormalizowaniu), niż pozwala na to typ zmiennej czyli precyzja. Np.: zapisując w zmiennej typu float wartość 2,5 nie popełnia się błędu zaokrąglenia gdyż wszystkie niezerowe cyfry po przecinku mieszczą się w obszarze zarezerwowanym na zmienną. Zapisując wartość 2,512341793176 popełniany jest błąd zaokrąglenia - zmienna typu float pozwala na zapamiętanie tylko 7-8 cyfr po przecinku (23 bity) zatem 0,000000003176 to reszta (błąd) po zaokrągleniu wartości w dół.

Skutki tego błędu są szczególnie istotne podczas sumowania liczb o dużej różnicy rzędów, kiedy konieczne jest zrównanie cechy. Jeżeli L1=A·10^-2, a L2=B·10², to sumowanie tych liczb wymaga sprowadzenia L1 do postaci L1=0,000A·10². Ponieważ zapamiętane zostaną jedynie cyfry do 8 miejsca po przecinku, to przesunięcie przecinka o 4 miejsca w lewo powoduje odrzucenie 4 ostatnich cyfr liczby A.

Błąd zaokrągleń występujący przy sumowaniu zostanie zilustrowany na przykładzie:

Funkcja

(2.1)

ma zawsze wartość 1.

Do licznika zostanie dodana i odjęta liczba A, co nie zmieni wartości funkcji.

(2.2)

Załóżmy, że liczby x i A różnią się o wiele rzędów (dla float 6..8).

Wykres wartości funkcji (2.2) dla A=1 i x typu float z przedziału <10^-8...10^-5> przedstawiono na rys. 2.1.

Rys. 2.1. Wpływ błędu zaokrągleń.

Obserwując wykres można wyróżnić trzy charakterystyczne obszary:

0<x<6·10^-8 Dodanie x do A powoduje „zniknięcie” wartości x. Odjęcie A całkowicie zeruje licznik, zatem wartość funkcji wynosi 0.

6·10^-8 <x<2·10^-7 Dodanie x do A daje wartość zaokrągloną. Odjęcie A, na skutek błędu, daje w liczniku wartość z zakresu 0,5·x .. 2·x, zatem wartość funkcji waha się w przedziale <0,5 ... 2>.

2·10^-7 <x Błąd zaokrąglenia ma wartość tak małą (w porównaniu z A i x), że nie wpływa ona znacząco na sumę A+x. Po odjęciu A w liczniku pozostaje wartość praktycznie równa x, zatem funkcja (2.2) osiąga wartość ≈1.

Przykład w C - obliczanie wyrażenia (2.2)

	#include <stdio.h> #include <conio.h> float a=1, z, x=6.00e-8; //x=1.78e-7; int main() { z=x+a; //tu powstaje błąd zaokrąglenia! z=(z-a)/x; printf("x/x=%f",z); getch(); return 0; }

Wynik: dla x=6,00·10^-8: x/x=1,986822

dla x=1,78·10^-7: x/x=0,669715

Przedstawiony przykład ilustruje skutki błędu zaokrągleń powstające tylko w jednej operacji dodawania. W praktyce obliczenia bywają bardzo złożone i wieloetapowe. Wartości obliczone wcześniej wykorzystuje się do obliczeń w dalszym etapie procesu numerycznego. Każda operacja dodawania i odejmowania obarczona jest błędem zaokrągleń a cząstkowych operacji dodawania/odejmowania w procesie numerycznym mogą być setki a nawet tysiące.

Wiedza o błędach oraz umiejętność ich oszacowania jest podstawą wiarygodności prowadzonych obliczeń.

Błąd przepełnienia w arytmetyce stałopozycyjnej

W czasie wykonywania operacji na liczbach całkowitych zdarza się przepełnić zmienną. Wówczas przepełnienie nie mieści się w obszarze przeznaczonym na zmienną i jest pomijane.

Przykład: Dane są dwie liczby jednobajtowe

A=01101011₂=6B₁₆=107

B=11010010₂=D2₁₆= 210

Po dodaniu powinny dać wynik 317 (9 bitów), ale w zmiennej jednobajtowej zmieści się tylko (8 bitów) zatem nastąpiło przepełnienie zmiennej.

317₁₀=1 00111101₂

Pierwsza, najbardziej znacząca cyfra (pogrubiona) zniknie. W zmiennej pozostanie 8 bitów:

00111101₂=61₁₀

Wartość 61₁₀ to reszta z dzielenia wyniku dodawania przez 256.

Podobne przepełnienie może wystąpić dla zmiennej dowolnego typu całkowitego.

2.4. Wyliczanie wartości funkcji złożonych - rozwinięcie w szereg potęgowy

Jak wspominano, komputer nie potrafi wyliczać wartości funkcji złożonych. Aby wykorzystać go do rozwiązania tego typu zadań, należy zaimplementować algorytm wyliczania tych funkcji. Z pomocą przychodzą rozwinięcia w szereg, które pozwalają na wyliczenie wartości funkcji złożonych z dowolną dokładnością, z wykorzystaniem operacji elementarnych.

Przykłady rozwinięcia wybranych funkcji

(2.4)

(2.5)

(2.6)

(2.7)

(2.8)

W taki sposób, wykorzystując jedynie operacje dodawania, odejmowania, mnożenia i dzielenia wyliczane są wartości funkcji złożonych.

2.5. Błąd obcięcia

Dokładną wartość wyliczanych funkcji uzyska się dodając wszystkie wyrazy szeregu. Niestety w granicach sumowania występuje nieskończoność, zatem dodanie wszystkich wyrazów jest niemożliwe i oczywiście niepotrzebne przynajmniej z dwóch powodów.

Po pierwsze operacja trwałaby nieskończenie długo. Po drugie, szeregi są zbieżne, co oznacza, że każdy kolejny wyraz jest mniejszy (co do modułu) od poprzedniego. Wartości kolejnych wyrazów dążą do 0 wraz ze wzrostem k. Dla dostatecznie dużego k, wartość k-tego wyrazu jest mniejsza od błędu zaokrąglenia i dodawanie go oraz następnych jest niecelowe, gdyż nie zmienia wartości dotychczas obliczonej sumy.

Wiedząc o tym nie dodaje się nieskończenie wielu wyrazów szeregu ale n pierwszych decydując się na wartość przybliżoną wyliczanej funkcji.

Zrealizujmy obliczenia na przykładzie funkcji exp(x).

(2.9)

(2.10)

Sumowanie do n powoduje pominięcie wyrazów n+1, n+2 itd. Nazywa się to obcięciem szeregu. Wyrazy obcięte to błąd wyliczanej wartości, który nazywany jest błędem obcięcia lub błędem metody.

Dokładna wartość błędu to suma wszystkich odrzuconych wyrazów (2.10). W praktyce nie ma potrzeby wyliczania aż tak precyzyjnej wartości. W większości przypadków wystarcza oszacowanie błędu obcięcia. Do wyliczenia szacunkowej wartości wykorzystuje się pierwszy (największy) z obciętych wyrazów. Dla funkcji exp(x) jest to:

(2.11)

Wykorzystując obcięte szeregi można obliczyć wartości funkcji złożonych w stosunkowo krótkim czasie i z dowolną dokładnością, znając przy tym wartość popełnianego błędu.

Do obliczenia wartości błędu obcięcia powraca się jeszcze w kolejnych rozdziałach pracy.

2.6. Schemat Hornera - redukcja operacji zmiennoprzecinkowych

Chociaż rozwinięcia w szereg dają możliwość wyliczania wartości funkcji złożonych, to wzory (2.4 - 2.8), nawet przy ograniczeniu sumowania do n wyrazów, zawierają nadmiarową liczbę operacji zmiennoprzecinkowych.

Operacje dodawania czy odejmowania wykonywane są zwykle w jednym cyklu pracy procesora. Operacja mnożenia jest bardziej czasochłonna, dzielenia, jeszcze bardziej. Mnożenie i dzielenie nie należy do operacji elementarnych (wykonywanych przez mikroprocesor wprost), wymaga algorytmu, który jest zwykle zaimplementowany w każdym języku programowania.

Ponieważ, w czasie wyliczania wartości funkcji złożonej, zmiennoprzecinkowych operacji arytmetycznych jest dużo, to każdy sposób zredukowania nakładu obliczeniowego (zmniejszenie ilości mnożeń i dzieleń) będzie miał znaczenie dla szybkości wykonywanych obliczeń.

Przykład

Wyliczmy wartość exp(x) wykorzystując 8 wyrazów szeregu:

(2.12)

Policzmy operacje arytmetyczne

nazwa operacji	dodawanie	mnożenie	dzielenie
ilość	7	21	6

Zredukujmy część mnożeń w (2.12) wyciągając wspólny czynnik: x przed nawias

(2.13)

Nastąpiło obniżenie wykładników potęg x w nawiasie. Spowodowało to redukcję 6 operacji mnożenia, kosztem jednego mnożenia wykonywanego dodatkowo.

nazwa operacji	dodawanie	mnożenie	dzielenie
ilość	7	16	6

Postępując podobnie, w kolejnych krokach wyciąga się przed nawias wspólny dzielnik pozostałych składników

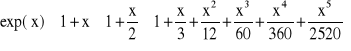
(2.14)

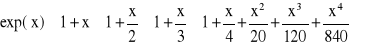
(2.15)

…

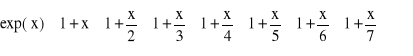
(2.16)

Zamieniając dzielenie na mnożenie przez odwrotność liczby uzyskuje się nakład obliczeniowy

nazwa operacji	dodawanie	mnożenie	dzielenie
ilość	7	12	0

Obliczanie wartości exp(x) ze wzoru (2.16) jest kilkadziesiąt razy szybsze niż w przypadku wzoru (2.12), a dokładność obliczeń jest taka sama lub nawet większa w przypadku (2.16) ze względu na mniejszy wpływ błędu zaokrągleń.

Ten sposób wyliczania wartości wielomianów nosi nazwę schematu Hornera.

2.7. Zadania dla studentów

2.1. Przedstaw liczby 13,81; 23,982; 17,11; 45,371 zgodnie z IEEE 754.

2.2. Zadeklaruj zmienną typu float, nadaj jej wartość. Odczytaj 4 bajty zajmowane przez tą zmienną i oblicz ręcznie jaka liczba przechowywana jest w zmiennej.

2.3. Zaproponuj schemat Hornera dla wyrażeń (2.4 … 2.8), porównaj nakład obliczeniowy.

2.4. Napisz w C++ program, który porówna czas wyliczania wartości exp(x) ze wzorów (2.12) i (2.16)

2.5. Napisz funkcje obliczające rekurencyjnie wyrażenia (2.4 ... 2.8) po wprowadzeniu schematu Hornera.

2.6. Wykorzystując podany w treści rozdziału program sporządź wykres jak z rys. 2.1. dla zmiennej typu double.

3. Numeryczne rozwiązywanie równań nieliniowych

W niniejszym rozdziale omówione zostaną metody rozwiązywania równania nieliniowego, czyli znajdowania miejsca zerowego funkcji nieliniowej. Zostanie przedstawionych kilka metod. Niektóre z nich wymagają powtórzenia wiadomości o pochodnych funkcji oraz o szeregu Taylora. Z zagadnieniem związany jest także problem zbieżności procesu iteracyjnego, któremu to poświęcony zostanie jeden z podrozdziałów.

3.1. Pochodna funkcji, rozwinięcie w szereg Taylora

Na wstępie przypomnijmy pojęcie ilorazu różnicowego i jego interpretację geometryczną.

Ilorazem różnicowym funkcji

(3.1)

w punkcie x₀ nazywa się iloraz przyrostu wartości funkcji do przyrostu wartości x. Jeżeli przyrost wartości x oznaczy się przez , to iloraz różnicowy zapisuje się

(3.2)

Rys. 3.1. Iloraz różnicowy - nachylenie siecznej.

Jeżeli przez punkty (x₀, ƒ(x₀)) i (x₀+x, ƒ(x₀+x)) przeprowadzona zostanie prosta, to taką prostą nazywa się sieczną i opisuje równaniem

(3.3)

współczynnik kierunkowy prostej (3.3) jest ilorazem różnicowym funkcji (3.1) w punkcie x₀.

(3.4)

3.1.1. Pochodna funkcji w punkcie - definicja

Rys. 3.2. Granica ilorazu różnicowego - definicja pochodnej funkcji.

Na rys. 3.2. przedstawiono sytuację, w której wartość przyrostu x jest niewielka. Kiedy x dąży do zera sieczna staje się styczną do krzywej w punkcie x₀, tangens kąta nachylenia stycznej (współczynnik kierunkowy) jest pochodną funkcji ƒ(x) w punkcie x₀.

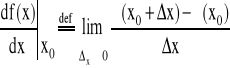
(3.5)

Pochodna funkcji w punkcie x₀ jest granicą ilorazu różnicowego w punkcie x₀
gdy x dąży do 0.

W niektórych sytuacjach, przy dostatecznie małej wartości x można przybliżać wartość pochodnej ilorazem różnicowym funkcji. Interpretacją geometryczną pochodnej jest styczna do krzywej.

3.1.2. Szereg Taylora

Rozwinięcie funkcji f(x) w szereg Taylora w otoczeniu punktu x₀ przedstawia wzór

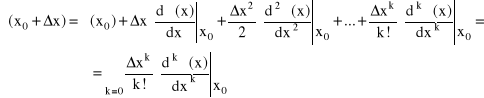
(3.6)

Jeżeli x₀=0, a wartość  oznaczy się x, to szereg przybiera postać:

(3.7)

i jest nazywany szeregiem Maclaurina.

Oba szeregi stosowane są bardzo często do rozwijania funkcji w szeregi potęgowe.

W dalszej części książki szereg Taylora będzie wykorzystywany do wyprowadzenia lub zilustro­wania niektórych z metod numerycznych.

Reszta szeregu

W wyrażeniu (3.6) sumowanie odbywa się w nieskończoność. Zaadaptowanie go w praktycznych zastosowaniach wymagać będzie (tak jak poprzednio) obcięcia. W tym przypadku obcięte wyrazy tworzą resztę Taylora (błąd obcięcia), którą przybliża się za pomocą wyrażenia:

(3.8)

Punkt  wybiera się dowolnie z przedziału (x₀…x₀+x).

Dla szeregu Maclaurina wyrażenie to jest identyczne, z tym, że  leży w przedziale (0…x).

Przykład

Rozwińmy funkcję exp(x) w szereg Maclaurina. Zgodnie ze wzorem (3.7) zapisuje się:

(3.9)

pochodna funkcji exp(x) ma postać exp(x) i dla zera przybiera wartość 1. Szereg (3.9) zapisuje się:

(3.10)

i jest to dokładnie taki wzór, jaki przedstawiono w rozdziale 2.

3.2. Metoda punktu stałego

Rozwiązywaniem równania nieliniowego jest poszukiwanie takiej wartości x₀ z dziedziny funkcji dla której wartość funkcji wynosi zero.

(3.11)

Teoria punktu stałego dotyczy równań postaci:

(3.12)

Metoda punktu stałego, nazywana często metodą iteracji prostej, polega na przekształceniu równania (3.11) w taki sposób, aby umieścić x po lewej stronie równania uzyskując (3.12).

(3.13)

W kolejnych iteracjach, wyliczoną wartość x' wstawia się do wyrażenia po prawej stronie w miejsce x₀ i wylicza kolejną wartość x' (3.13). Iteracje kończą się po uzyskaniu założonej dokładności.

Do zademonstrowania działania metody obliczmy wartość  przedstawioną w rozdziale 1, korzystając z jej własności (1.6). Przepiszmy:

(3.14)

i przekształćmy do postaci (3.12)

(3.15)

Przyjmijmy dowolny punkt startowy z dziedziny funkcji np.: x₀=1 i wykonajmy kilka iteracji …

iteracja	wartość początkowa	wartość wyliczona	moduł różnicy |x'0-x0|
1	1 (start)	2	1
2	2	1,5	0,5
3	1,5	1,66(66)	0,166(66)
4	1,66(66)	1,6	0,06(66)
5	1,6	1,625	0,025
6	1,625	1,6(153846)	0,0096(153846)

Po 6 iteracjach uzyskano wartość 1,6(153846). Proces jest zbieżny, gdyż moduł różnicy maleje z każdym krokiem iteracji. W następnym 7. kroku byłby zatem jeszcze mniejszy. Moduł różnicy można traktować jako górną granicę niedokładności obliczeń (błąd obliczeń).

Dokładna wartość  mieści się zatem w przedziale 1,6(153846)±9,6(153846)·10^-3.

Warto sprawdzić jaki błąd rzeczywiście popełniono i czy leży on w granicach podanego oszacowania.

Rozwiązując analitycznie zadanie 1.4 uzyskuje się

(3.16)

Różnica między wartością (3.16) a naszym przybliżeniem wynosi 2,649·10^-3 i jest mniejsza od założonego błędu (ostatniej różnicy).

Aby wyliczyć wartość  z dowolną dokładnością  należy prowadzić proces iteracyjny do momentu aż moduł różnicy będzie mniejszy od .

Kontrolowanie modułu różnicy uzyskanych iteracyjnie wartości jest typowe dla wszystkich metod rozwiązywania równań nieliniowych.

3.2.1. Ilustracja graficzna metody iteracji prostej

W metodzie punktu stałego, po obu stronach równania (3.12, 3.13) występują funkcje zmiennej x.

(3.17)

(3.18)

Funkcję ƒ(x)+x, która także jest funkcją zmiennej x, nazwano f₁(x).

Przedstawmy przebieg tych funkcji na wykresie.

Rys. 3.3. Graficzna interpretacja metody punktu stałego.

Linią niebieską zaznaczono przebieg funkcji y=x, linią czerwoną y= ƒ₁(x).

Jeżeli krzywe się przecinają, to równanie nieliniowe ma rozwiązanie.

Iteracje przebiegają zgodnie z zaznaczoną na szaro drogą:

- punkt x₀, jest punktem startowym procesu;

- wyliczana jest wartość y= ƒ₁(x₀);

- wartość y podstawiana do równania y=x, z którego wyliczana jest nowa wartość x₀.

Z rysunku 3.3. widać, że proces iteracyjny jest raczej wolnozbieżny.

Metoda punktu stałego jest jedną z najprostszych metod rozwiązywania równań nieliniowych.

3.2.2. Przykład implementacji

Program rozwiązuje równanie nieliniowe (3.14), czyli oblicza wartość „złotej liczby”.

	#include <stdio.h> #include <conio.h> #include <math.h> float x,xo,e; int i; int main() { e=1E-6; xo=1; x=2; i=0; while(fabs(xo-x)>e) { i++; x=xo; xo=1/x+1; } printf("Fi=%f, obliczono w %d iteracjach",xo,i); getch(); return 0; }

Program wyświetla: Fi=1.618034 , obliczono w 16 iteracjach.

3.3. Metoda bisekcji (równego podziału)

3.3.1. Twierdzenie (Bolzano−Cauchy'ego)

Jeśli funkcja f(x) jest ciągła w przedziale <A...B> i przybiera na krańcach tego

przedziału dwie różne wartości: ƒ(A)=p, ƒ(B)=q p<q i jeśli r jest pewną liczbą zawartą między tymi wartościami: p<r<q, to istnieje wewnątrz przedziału <A...B> punkt C, w którym funkcja ƒ(x) przybiera wartość r: ƒ(C)=r.

3.3.2. Opis metody równego podziału

Metoda bisekcji, zwana także metodą połowicznego podziału czy równego podziału jest intuicyjną metodą rozwiązywania równania nieliniowego, chociaż bazuje na twierdzeniu Bolzano-Cauch'ego przytoczonym w poprzedniej części.

Jeżeli wiadomo, że miejsce zerowe funkcji zawarte jest w przedziale domkniętym <A..B>, co łatwo sprawdzić, gdyż przecinając oś OX funkcja zmienia znak, zatem iloczyn:

(3.19)

to poszukiwanie rozwiązania odbywa się przez dzielenie przedziału <A..B> na dwie równe części: <A..x₀..B>, gdzie

(3.20)

wartość x₀ jest pierwszym przybliżeniem rozwiązania równania.

W kolejnym kroku należy zbadać, w którym z powstałych przedziałów leży rozwiązanie. Warunek (3.19) sprawdzany jest dla krańców przedziału <A..x₀>.

Mogą wystąpić trzy przypadki:

1.
Rozwiązanie znajduje się w <A..x₀>

2.
Rozwiązaniem jest x₀

3.
Rozwiązanie znajduje się w <x₀..B>

Jeżeli wystąpi przypadek 2. iteracje kończą się, a rozwiązaniem jest x₀. Jeżeli wystąpi 1. przypadek, do B wstawia się wartość x₀ i przechodzi do obliczenia nowej wartości x₀ ze wzoru (3.20). Jeżeli wystąpi przypadek 3., do A wstawia się x₀ i oblicza nowe x₀. W każdym kroku iteracji przedział <A..B> zawęża się dwukrotnie.

Iteracje kończą się jeżeli kiedykolwiek wystąpi przypadek 2, lub jeżeli moduł różnicy kolejno wyliczonych wartości x₀ jest mniejszy od , co w tej metodzie odpowiada połowie badanego przedziału <A..B>.

Wykorzystanie tej metody jest możliwe, jeżeli spełnione są warunki:

1. Funkcja ƒ(x) jest ciągła w przedziale <A..B>.

2. Na krańcach przedziału wartości funkcji mają różne znaki.

3.3.3 Ilustracja graficzna metody bisekcji

Rys. 3.4. Ilustracja kolejnych iteracji w metodzie bisekcji - zawężanie przedziału poszukiwań.

3.4. Metoda siecznych

Metoda siecznych znana jest także pod nazwą metody interpolacji liniowej, czy metody Eulera. Różni się od metody bisekcji jedynie sposobem wyliczania wartości x₀ (dzielenia przedziału na części). Pozostała część algorytmu pozostaje bez zmian. Prawa algebry na których opiera się metoda siecznych oraz warunki związane ze stosowaniem są też takie same.

W tej metodzie dzieli się przedział na części prowadząc prostą (sieczną) przez punkty (A,ƒ(A)) i (B,ƒ(B)).

Prosta przechodząca przez te punkty będzie miała współczynnik kierunkowy

(3.21)

(porównaj z ilorazem różnicowym (3.4))

Równanie siecznej podano już wcześniej (3.3), ale przepiszmy je uwzględniając (3.21)

(3.22)

Punkt podziału przedziału <A..B>, czyli nowe miejsce zerowe x₀ znajduje się rozwiązując równanie (3.22) względem x dla y=0.

(3.23)

Metoda siecznych uwzględnia charakter krzywej ƒ(x) zatem zbieżność zależy od kształtu krzywej i może być zarówno większa jak i mniejsza niż w metodzie bisekcji.

Dla przykładu z rys. 3.4. poprowadzenie pierwszej siecznej daje znacznie gorsze przybliżenie miejsca zerowego niż podział przedziału <A..B> na połowę. Jest to przykład wolniejszej zbieżności metody siecznych w porównaniu z met. bisekcji.

3.4.1. Ilustracja graficzna metody siecznych

Na rys. 3.5. pokazano inną sytuację, zaznaczając 3 kolejne przybliżenia rozwiązania. Na wykresie można dostrzec, że dokładne rozwiązanie jest oddalone od kolejnego przybliżenia x₀ nie bardziej niż moduł różnicy dwóch kolejnych przybliżeń. Jak wspomniano wcześniej, wartość tego modułu jest szacunkowym błędem numerycznego rozwiązania równania nieliniowego.

Rys. 3.5. Iteracje w metodzie siecznych.

3.5. Metoda stycznych (Newtona-Raphsona)

Metodą rozwiązywania równań nieliniowych o najszybszej zbieżności, a zatem najefekty­wniejszą, jest metoda Newtona-Raphsona. Wykorzystuje ona wartość pochodnej funkcji w punkcie x₀ do przybliżenia prostą przebiegu funkcji. Prosta przecina oś OX w punkcie, który staje się kolejnym przybliżeniem rozwiązania.

Oznaczmy pochodną funkcji jako g(x).

(3.24)

Wartość pochodnej jest współczynnikiem kierunkowym stycznej. Równanie stycznej do krzywej ƒ(x) w punkcie x₀ zapisuje się w postaci:

(3.25)

Nowym przybliżeniem miejsca zerowego jest rozwiązanie równania (3.25) względem x dla y=0.

(3.26)

Proces iteracyjny w metodzie stycznych zilustrowano na rys. 3.6.

Rys. 3.6. Kolejne iteracje metodą stycznych.

Ponieważ do przybliżenia kolejnego miejsca zerowego wykorzystuje się pochodną, a różniczko­wanie należy do operacji źle uwarunkowanych numerycznie, należy spełnić więcej warunków niż w przypadku wcześniej omawianych metod:

- w przedziale [A...B] znajduje się dokładnie jeden pierwiastek;

- wartości funkcji mają różne znaki na końcach przedziału;

- pierwsza i druga pochodna nie zmienia znaku w przedziale <A...B>.

Szczególnie istotny jest trzeci warunek gdyż badanie przebiegu 2. pochodnej jest często niemożliwe. Niespełnienie warunku może prowadzić do rozbieżności w procesie iteracyjnym.

Jako punkt startowy należy wybrać ten kraniec przedziału <A...B> w którym znak funkcji i jej drugiej pochodnej jest jednakowy.

3.5.1 Obliczanie pierwiastka liczby

Szczególnym przypadkiem zastosowania metody Newtona-Raphsona jest wyliczanie wartości pierwiastka z liczby z dowolną dokładnością. Pierwiastek z liczby A można zapisać w postaci równania

(3.27)

Zapisuje się funkcję oraz jej pochodną

(3.28)

(3.29)

Po przyjęciu punktu startowego x kolejne przybliżenia x' liczy się ze wzoru (3.26). Dla naszego przypadku przybiera on postać:

(3.30)

Jak określić punkt startowy?

Niech A=11. Ponieważ znane są pierwiastki kwadratowe liczb 9 i 16, zatem pierwiastek z 11 spełnia warunek 3<x<4 (patrz rozdz. 3.3.1.). Przyjmijmy pierwsze przybliżenie w połowie przedziału <3…4>: x=3,5 (do lepszego oszacowania wrócimy przy omawianiu strategii wyboru punktu startowego).

Wówczas w kilku iteracjach obliczamy:

1.

2.

3.

Po trzeciej iteracji różnica kolejnych, obliczonych iteracyjnie, wartości pierwiastka, a więc górna granica błędu, wynosi około 3,474·10^-6. W rzeczywistości, pomiędzy naszym oszacowaniem a wartością dokładną pierwiastka z 11 jest różnica 1,819·10^-12.

Metodą Newtona można liczyć pierwiastki dowolnego stopnia liczb dodatnich. Przy odpowiednim doborze punktu startowego, w większości przypadków wystarczające są dwie iteracje.

3.6. Warunki zbieżności procesu iteracyjnego, strategia wyboru punktu startowego

{Koniecznie dopisać ten rozdział}

3.7. Zadania

3.1. Wykorzystując szereg Maclaurina rozwiń funkcje sin(x) i cos(x).

3.2. Rozwiąż „ręcznie” metodą punktu stałego: ln(x)+2-x=0; exp(x)-3x-1=0. Spróbuj rozwiązać tą metodą kilka dowolnych funkcji. Jakie otrzymasz wyniki? - skomentuj.

3.3. Napisz program rozwiązujący równanie nieliniowe metodą bisekcji i siecznych. Dla kilku funkcji porównaj ilość iteracji w obu metodach przy tej samej dokładności.

3.4. Napisz funkcję float pierwNR(float a, int k, float e) wyliczającą pierwiastek k-tego stopnia z a metodą Newtona z dokładnością .

3.5. Dlaczego pojęcie „pierwiastek” używane jest zarówno dla pierwiastka z liczby i dla miejsca zerowego funkcji?

3.6. Oblicz iteracyjnie:
,
,

3.7. Do programu z zad. 3.2. dodaj metodę Newtona-Raphsona i dokonaj ponownie porównania.

3.8. Czy można obliczać pierwiastki metodą bisekcji i siecznych? Napisz odpowiednie funkcje w języku C.

3.9.

3.10.

4. Całkowanie numeryczne

Niniejszy rozdział poświęcono metodom numerycznego rozwiązywania całek oznaczonych za pomocą wybranych algorytmów DEI (Differential Equation Integration). Przed omawianiem konkretnych metod przypomnijmy jednak problem całkowania, właściwe dla niego nazewnictwo, oznaczenia oraz przybliżmy pojęcie całki.

4.1. Funkcja pierwotna, interpretacja geometryczna całki.

Podstawowye twierdzenie rachunku całkowego: operacje całkowania i różniczkowania są operacjami odwrotnymi.

W równaniu

(4.1.)

funkcja F(x) nazywana jest funkcją pierwotną do ƒ(x), a ƒ(x) jest pochodną F(x) i słuszny jest zapis

(4.2)

W takim przypadku ƒ(x) może być nazywana funkcją podcałkową.

O ile interpretacją geometryczną pochodnej funkcji jest styczna do krzywej, a dokładniej współczynnik kierunkowy stycznej, o tyle geometryczną interpretacją całki oznaczonej w przedziale <A...B> jest pole pod krzywą ƒ(x) ograniczone osią OX oraz prostymi x=A i x=B, i można je wyliczyć z dowolną dokładnością za pomoca skończonej liczby prostokątów. Jest to definicja podana przez niemieckiego matematyka Bernardha Riemanna. Całkę oznaczoną w przedziale <A … B> zapisuje się:

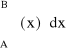
(4.3)

Rys. 4.1. Interpretacja geometryczna całki oznaczonej w sensie Riemanna.

Wiele metod numerycznego całkowania bazuje wprost na definicji Riemanna.

Dla jasności treści zawartych w tym rozdziale wprowadźmy klasyfikację zadań realizowanych za pomocą algorytmów DEI.

1. Obliczanie całki oznaczonej - funkcja podcałkowa ƒ(x) jest znana, wyliczana jest wartość liczbowa określająca pole pod krzywą.

2. Rozwiązywanie równania różniczkowego - funkcja podcałkowa jest znana, wylicza się zbiór wartości funkcji pierwotnej w konkretnych punktach (węzłach).

3. Rozwiązywanie zagadnień początkowych - wartość funkcji ƒ(x) jest znana jedynie w chwili startu iteracji (warunek początkowy). Oblicza się zbiór wartości funkcji ƒ(x) i F(x) w konkretnych punktach dziedziny (węzłach).

Treści niniejszego rozdziału dotyczą jedynie pierwszego i drugiego przypadku. Przypadek trzeci zaprezentowany zostanie jedynie jako przykład zadania w końcowej części.

4.2. Metody prostokątów.

Załóżmy, że przybliżymy wartość pola powierzchni pod krzywą ƒ(x) ze skończoną dokładnością. Dzieląc przedział <A...B> na n przedziałów (chwilowo równych) i wyznaczając wartość funkcji ƒ(x) na krańcach każdego z nich, można obliczyć przybliżoną wartość pola pod krzywą ƒ(x) w przedziale mnożąc wartość funkcji i szerokość przedziału. Szacunkowa wartość całki oznaczonej w przedziale <A...B> będzie sumą pól wszystkich powstałych prostokątów.

Oznaczmy:

h - krok całkowania, szerokość każdego z przedziałów;

k - kolejna iteracja w procesie całkowania;

(4.4)

(4.5)

Aby policzyć pole k-tego prostokąta należy pomnożyć szerokość jego podstawy (h) i wysokość. Istnieją dwa sposoby realizacji tego zadania. Jako wysokość prostokąta można przyjąć wartość funkcji w punkcie x_k→ƒ(x_k) (początek przedziału) lub w punkcie x_k+1→ƒ(x_k+1) (koniec przedziału).

Istnieją więc dwie metody prostokątów. Ponieważ wzory (algorytmy) całkowania numerycznego zapisuje się zwykle rekursywnie zatem:

(4.6)

Wzór prostokątów nazywany ekstrapolacyjnym algorytmem Eulera

(4.7)

Wzór prostokątów nazywany interpolacyjnym algorytmem Eulera,

gdzie:

F_k - wartość funkcji pierwotnej w k-tym kroku;

ƒ(x_k) - wartość funkcji w k-tym kroku (dla x_k);

h - krok całkowania;

W_p - warunek początkowy, dla całkowania zwykle równy 0.

a)
b)

Rys. 4.2. Ilustracja graficzna całkowania metodami Eulera: a) algorytm ekstrapolacyjny, b) algorytm interpolacyjny.

Oba algorytmy mają tę samą klasę dokładności (rząd) i w przypadku wyliczania całki oznaczonej nie ma większej różnicy, który ze wzorów zostanie wykorzystany. Różnica pojawia się dopiero przy próbie zastosowanie ich do rozwiązywania zagadnienia początkowego, kiedy oprócz dokładności rozważa się także stabilność numeryczną algorytmów.

Przykład 4.1.

Program oblicza całkę oznaczoną wielomianu ƒ(x)=-x³+x²+5x+5 w przedziale <0...3> metodami Eulera, liczy wartość dokładną i błędy obliczeń numerycznych.

	#include <stdio.h> #include <math.h> #include <conio.h> float Calka(float a, float b) // obliczanie wartości całki analitycznie { float f,g; f=a*(5.0+a*(2.5+a*(1.0/3-a/4))); g=b*(5.0+b*(2.5+b*(1.0/3-b/4))); return g-f; } float f_od_x(float x) // obliczanie wartości funkcji podcałkowej { float f; f=5+x*(5+x*(1-x)); return f; } int main() { int i,n=50; float f, fam1=0, fab1=0, dam1, dab1, a, b, h, x; a=0; b=3; x=a; h=(b-a)/n; f=Calka(a,b); for (i=0;i<n;i++) // obliczanie całki metodami numerycznymi { fab1=fab1+h*f_od_x(x); fam1=fam1+h*f_od_x(x+h); x=x+h; } dam1=100*fabs((fam1-f)/f); // obliczanie błędów względnych dab1=100*fabs((fab1-f)/f); printf("Dokladna wartosc calki wynosi: %2.3f\n\r",f); printf("\n\r Interpolacyjny Eulera: %2.3f - blad %2.2f%%",fam1,dam1); printf("\n\rEkstrapolacyjny Eulera: %2.3f - blad %2.2f%%",fab1,dab1); getch(); return 0; }

4.2. Podział metod całkowania numerycznego

Według podstawowego kryterium wszelkie algorytmy całkowania dzieli się na dwie grupy: jednokrokowe i wielokrokowe, wewnątrz grup wprowadza się dodatkowe podziały.

Wyliczenie wartości całki w kroku k+1 sprowadza się do dodania do wartości całki z poprzedniego kroku przybliżonej wartości P pola figury pod krzywą ƒ(x) w przedziale <x_k..x_k+1>.

(4.8)

W algorytmach jednokrokowych wartość P_k+1 przybliża się wykorzystując jedynie wartości z bieżącego kroku: z przedziałów <x_k…x_k+1>, <ƒ(x_k)...ƒ(x_k+1)>, to oznacza, że przedział dzieli się dodatkowo na części, oblicza pośrednie wartości funkcji ƒ(x), zwykle wykorzystując rozwinięcie w szereg Taylora, w przedziale <x_k…x_k+1>.

Algorytmy wielokrokowe przybliżają wartość P_k+1 w inny sposób. Wykorzystuje się wartości ƒ(x_k) tylko z krańców przedziałów, ale obliczone także w poprzednich krokach. Wybierając wartości wyliczone nawet kilka kroków (s - step) wcześniej dokonuje się interpolacji wielomianowej funkcji ƒ(x) w zbiorze wartości dyskretnych {(x_k+1-s,ƒ(x_k+1-s)); (x_k+1-s+1,ƒ(x_k+1-s+1)); (x_k+1,ƒ(x_k+1))}.

a)
b)

Rys. 4.3. Ilustracja działania algorytmów: a) jednokrokowych; b) wielokrokowych.

Algorytmy jednokrokowe wymagają wyliczenia wartości funkcji ƒ(x) w kilku punktach z przedziału <x_k…x_k+1>, wartości te nie będą wykorzystane w kolejnym kroku całkowania. Algorytmy wielokrokowe bazują jedynie na znanych wartościach z przeszłości procesu. Wynika z tego, że jednokrokowe metody całkowania są mniej efektywne, mają jednak pewną przewagę nad algorytmami wielokrokowymi gdyż wartość kroku h może być dobierana dowolnie dla każdego k+1. W algorytmach wielokrokowych zmiana wartośc h niesie pewne trudności związane z interpolacją wcześniejszych wartości {ƒ(x_k+1-s) … ƒ(x_k+1)}. Dodatkowo algorytmy wielokrokowe nie są samostartujące, gdyż do pracy wymagają s wartości poprzednich, których w pierwszym kroku po prostu nie ma.

Przedstawione wcześniej algorytmy Eulera należą do grupy wielokrokowych, ale do różnych rodzin. Analizując ich nazwy można domyślać się istnienia rodziny wielokrokowych algorytmów interpolacyjnych i ekstrapolacyjnych. Ta pierwsza nazywana jest rodziną algorytmów Adamsa-Moultona, druga Adamsa-Bashfortha. Interpolacyjny algorytm Eulera jest zarazem algorytmem Adamsa-Moultona 1. rzędu, a ekstrapolacyjny algorytm Eulera jest algorytmem Adamsa-Bashfortha 1. rzędu.

Należy wyjaśnić, że algorytmy (4.6 .. 4.7) wykorzystywane są przede wszystkim do rozwiązywania zagadnień początkowych, kiedy ani analityczna postać funkcji podcałkowej ani funkcji pierwotnej nie jest znana. Znane są jedynie warości w tzw. węzłach, czyli na krańcach kolejnych przedziałów całkowania {(x_k,ƒ(x_k),F(x_k); (x_k+1,ƒ(x_k+1),F(x_k+1)}. Gdyby znane były wartości funkcji ƒ(x) nie tylko w węzłach ale w dowolnym punkcie należącym do <x_k...x_k+1>, można stworzyć nieskończenie wiele metod prostokątów wybierając dowolną wysokość prostokąta z zakresu <ƒ(x_k).. ƒ(x_k+1)>. Takie metody jednokrokowe byłyby znacznie dokładniejsze od metod wielokrokowych.

Ponieważ w przedziale <x_k.. x_k+1> istnieje punkt , taki, że:

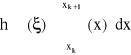
(4.9)

gdzie: (x_k+1-x_k)=h.

Szczególne znaczenie ma jednokrokowa metodą prostokątów znana jako metoda punktu środkowego, modyfikowany algorytm Eulera lub algorytm Eulera-Cauchy'ego.

(4.10)

Rys. 4.4. Ilustracja graficzna całkowania metodą punktu środkowego.

Jest to algorytm drugiego rzędu pochodzący z rodziny jednokrokowych algorytmów Rungego-Kutty, o których będzie mowa w następnym rozdziale. Algorytmem pierwszego rzędu w tej rodzinie jest ekstrapolacyjny algorytm Eulera.

4.3. Algorytmy wyższych rzędów

Metody Eulera (pierwszego rzędu) przybliżały kształt funkcji w przedziale <x_k...x_k+1> wartością stałą, czyli inaczej dokonywły interpolacji ƒ(x) wielomianem stopnia zerowego, i wyliczano pole prostokąta. Błąd popełniany w każdym kroku całkowania wynikał z różnicy pomiędzy powierzchnią pola prostokątów a polem figury pod krzywą. Możliwe jest dokładniejsze wyliczenie wartości całki poprzez zawężenie przedziałów całkowania, ale prowadzi to do wydłużenia czasu obliczeń. Dodatkowo, przy zbyt małym kroku, decydujące znaczenie ma błąd zaokrągleń, który uniemożliwi wyliczenie całki z dowolną dokładnością.

4.3.1. Algorytmy wielokrokowe [D3]

Inną techniką jest zastosowanie wielomianu wyższego stopnia do przybliżenia (interpolacji) kształtu krzywej w przedziale <x_k...x_k+1>, co powoduje redukcję będu obcięcia algorytmu i w konsekwencji wzrost dokadności obliczeń.

Zastosujmy wielomian 1. go stopnia prowadząc prostą przez (x_k,ƒ(x_k)) i (x_k+1,ƒ(x_k+1)). Pole tak uzyskanego trapezu będzie dane wzorem:

(4.11)

a odpowiadający mu algorytm całkowania numerycznego przyjmie postać:

(4.12)

Wzór (4.12) przedstawia algorytm trapezów, który jest algorytmem Adamsa-Moultona 2. rzędu i jest o rząd dokładniejszy od wielokrokowych metod prostokątów (Eulera).

Rys. 4.5. Ilustracja graficzna całkowania algorytmem trapezów.

Pomimo zastosowania wielomianu 1. stopnia w algorytmie trapezów, rzeczywisty kształt całkowanej krzywej nie odpowiada trapezom, zatem i w tym przypadku popełnia się błąd.

Wyprowadza się zatem zarówno interpolacyjne jak i ekstrapolacyjne wielokrokowe metody wyższych rzędów wykorzystujące wielomiany wyższych stopni.

a)
b)

Rys. 4.6. Algorytmy 3. rzędu: a) interpolacyjny Adamsa-Moultona; b) ekstrapolacyjna Adamsa-Bashfortha.

Ogólnie wielokrokowe algorytmy całkowania równań różniczkowych zapisuje się w postaci równania

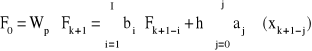
(4.13)

Współczynniki a_j i b_i występujące w tym równaniu, w zależności od typu algorytmu i jego rzędu zestawiono w tab. 4.1 i 4.2

Tab. 4.1. Algorytmy całkowania numerycznego z rodziny Adamsa-Moultona (interpolacyjne).

	współczynniki
Rząd	a0	a1	a2	a3	a4		b1		inna nazwa
1									interpolacyjny algorytm Eulera, metoda prostokątów
2									algorytm trapezów
3
4
5

Tab. 4.2. Algorytmy całkowania numerycznego z rodziny Adamsa-Bashfortha (ekstrapolacyjne).

	współczynniki
Rząd	a1	a2	a3	a4	a5		b1		inna nazwa
1									ekstrapolacyjny algorytm Eulera, prostokątów
2
3
4
5

4.3.2. Algorytmy jednokrokowe [D.2]

Wśród algorytmów jednokrokowych najistotniejsze znaczenie ma rodzina algorytmów Rungego-Kutty. Algorytmy te wyprowadza się z rozwinięcia w szereg Taylora (modyfikując algorytm Taylora). Ogólnie zapisuje się

(4.14)

K_R ma znaczenie współczynnika obliczanego inaczej dla każdego rzędu algorytmu Rungego-Kutty.

Dla algorytmu rzędu 2. parametr ten ma postać

(4.15)

Występuje tu wartość a₂ przyjmowana arbitralnie, która pozwalaja na wyprowadzennie nieskończenie wielu algorytmów rzędu drugiego. Podobnie jest w algorytmach wyższych rzędów.

Dla rzędu drugiego istotne są 2 przypadki: a₂=1, który prowadzi do przedstawionego wcześniej algorytmu Eulera-Cauchy'ego (4.10), oraz a₂=1/2, który jest znany jako algorytm Heuna i w przypadku operowania funkcją jednej zmiennej prowadzi do algorytmu trapezów (4.12). Jednak algorytm Heuna nie jest algorytmem trapezów, formalnie należałoby zapisać:

(4.16)

Algorytm ten nosi czasem nazwę modyfikowanego algorytmu trapezów.

Ze względu na możliwość zastosowania większego kroku całkowania i większą dokładność, najczęściej wykorzystywanym algorytmem Rungego-Kutty jest algorytm rzędu czwartego. Zapisuje się go w postaci (4.14) ze współczynnikiem:

(4.17)

gdzie:

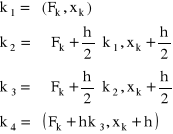
przykład

Obliczanie wartości całki funkcji ƒ(x)=-x³+x²+5x+5 w przedziale <0...3> metodą Rungego-Kutty rzędu czwartego.

Należy zauważyć, że dla funkcji jednej zmiennej współczynniki pomocnicze k_i we wzorze (4.17) upraszczają się do postaci:

(4.18)

Współczynnik K4 można zatem zapisać:

(4.19)

	#include <stdio.h> #include <math.h> #include <conio.h> float Calka(float a, float b) { float f,g; f=a*(5.0+a*(2.5+a*(1.0/3-a/4))); g=b*(5.0+b*(2.5+b*(1.0/3-b/4))); return g-f; } float f_od_x(float x) { float f; f=5+x*(5+x*(1-x)); return f; } float rgK4(float x, float h) { float k, k1, k23, k4; k1=f_od_x(x); k23=f_od_x(x+h/2); k4=f_od_x(x+h); k=(k1+4*k23+k4)/6; return k; } int main() { int i,n=50; //frg4 - wartość całki obl. met. Rungego-Kutty 4. rzędu float f, frg4=0, drg4, a, b, h, x; a=0; b=3; x=a; h=(b-a)/n; f=Calka(a,b); for (i=0;i<n;i++) { frg4=frg4+h*rgK4(x,h); x=x+h; } drg4=100*fabs((frg4-f)/f); printf("Dokladna wartosc calki wynosi: %2.3f\n\r",f); printf("\n\rRunge-Kutta R4: %2.3f - blad %2.3e%%",frg4,drg4); getch(); return 0; }

4.4. Algorytmy Geara

Szczególnie istotną rodziną algorytmów wielokrokowych są sztywno-stabilne algorytmy Geara. W niniejszym opracowaniu pomija się omawianie cech numerycznych algorytmów, ograniczając się do dokładności i stwierdzenia, że rośnie ona wraz rządem. Jest to oczywiście prawda, ale istnieją także inne cechy decydujące o jakości algorytmu. Bardzo istotna jest ich stabilność. Jeszcze ważniejsza jest ich odporność na całkowanie ze zbyt dużym krokiem, cecha ta nazywa się stabilnością sztywną. Algorytmy Geara, jako jedyne, są sztywno-stabilne i wykorzy­stywane powszechnie do rozwiązywania układów równań różniczkowych (zagadnień początko­wych, także nieliniowych) bardzo często w dziedzinie czasu. Są to programy do symulacji najróżniejszych zjawisk fizycznych. Dużą grupę stanowią symulatory obwodów elektronicznych.

W niniejszym rozdziale zaprezentowany zostanie przykład porównujący „jakość” rozwiązania otrzymanego z udziałem alghorytmu Geara i innych algorytmów.

W tabeli (4.2) podano wartości współczyników algorytmów Geara. Współczynniki odnoszą się do ogólnego równania (4.13), należy zwrócić uwagę że w odróżnieniu do podawanych dotychczas, w algorytmach Geara istnieje tylko jeden współczynnik a_j i wiele współczynników b_i.

Tab. 4.2. Algorytmy Geara.

	współczynniki
Rząd	b1	b2	b3	b4	b5		a0		inna nazwa
1									interpolacyjny algorytm Eulera, prostokątów
2
3
4
5

przykład - ilustracja wybranych cech algorytmów

Zastosujmy poznane algorytmy do rozwiązywania układu równań różniczkowych (zagadnienia początkowego) w obwodzie elektrycznym jak na rys. 4.6. Przedtem zapiszmy równania, które opisują ten obwód.

Rys. 4.6. Schemat obwodu elektrycznego.

Na początek należy zauważyć równania różniczkowe w tym obwodzie. Otórz kondensator należy do elementów inercyjnych. Pomiędzy funkcją prądu i napięcia na jego zaciskach zachodzi związek.

, stąd
(4.20)

Jeżeli zauważone zostanie, że:

F(t)=u_C(t); ƒ(t)=1/C·i_C(t), to można wprost zastosować którykolwiek ze wzorów całkowania. Dla algorytmu trapezów równanie to przybiera postać

(4.21)

Z tą różnicą, że indeks k zapisano w nawiasach kwadratowych ze względu na indeks C w nazwach zmiennych.

W programach do symulacji obwodów elektronicznych zwykle stosuje się technikę tzw. modeli stowarzyszonych z algorytmem wydzielając w równaniu (4.21) składniki związane z krokiem k+1 od pozostałych. Technika ta znacznie ułatwia analizę podobnych zadań.

(4.22)

Składnik w nawiasie klamrowym (znany z przeszłości procesu iteracyjnego) ma wymiar napięcia i może być zastępczym źródłem napięciowym uz_C a składnik poza nawiasem to iloczyn prądu kondensatora w kroku k+1 i pewnej rezystancji zastępczej Rz_C.

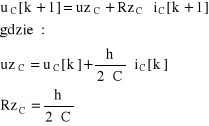
(4.23)

Stosując technikę modeli stowarzyszonych można dla obwodu z Rys. 4.6. narysować zastępczy model dyskretny.

Rys. 4.7. Zastępczy model dyskretny obwodu elektrycznego z Rys. 4.6.

Należy zauważyć, że struktura modelu pozostanie stała dla każdego k. Będą natomiast ulegały zmianie wartości źródeł zastępczych uz i ewentualnie zastępczych rezystancji Rz (o ile zmieni się krok całkowania). Warto dodać, że wartości elementów zastępczych będą różnie wyliczane dla różnych algorytmów.

Dla obwodu o charakterze rezystancyjnym w który przekształcił się obwód z Rys. 4.6. łatwo jest zapisać właściwe równania wynikające z praw Kirchhoffa i wyeliminować wszystkie niewiadmowe za wyjątkiem jednej, np. u₁.

(4.24)

stąd otrzymuje się:

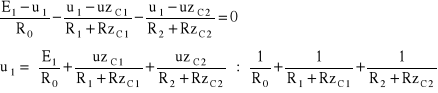
(4.25)

Dalsze przekształcenia algebraiczne pozwalają na wyliczenie pozostałych niewiadomych w szczególności napięć i prądów kondensatorów. Wyliczenia te będą prowadzone w każdym k-tym kroku.

Przyjęto następujące wartości elementów obwodu:

R0=2; R1=5,6·10³; R2=220; C1=470·10^-9F; C2=330·10^-6F;

Źródło E₁ generuje przebieg prostokątny o amplitudzie 1.

W obliczeniach dobrano krok h=16,5ms aby pokazać zachowanie algorytmów.

Rozpisano równania w programie MathCad i przeprowazono analizę obwodu za pomocą trzech algorytmów: Adamsa-Moultona 3. rzędu, trapezów i Geara 2. rzędu. Przebiegi obliczonych napięć na kondensatorach przedstawiają trzy kolejne wykresy.

Rys. 4.8. Przebieg napięć na kondensatorach w wyniku symulacji z algorytmem Adamsa-Moultona 3. rzędu.

Obliczone napięcie na kondensatorze C1 obarczone jest błędem, który narasta stopniowo w każdym kroku - jest to przykład braku stabilności numerycznej.

Rys. 4.9. Przebieg napięć na kondensatorach w wyniku symulacji z algorytmem Adamsa-Moultona 2. rzędu.

Wynik symulacji jest stabilny, niestety w chwilach nagłych zmian stanu obwodu pojawia się błąd w wyliczaniu napięcia uC1, który jest w tym przypadku tłumiony, ale często utrzymuje stałą amplitudę (choć nie narasta). Algorytm trapezów jest zawsze stabilny (A-stabilny), pomimo tego często zdarza się przekazywanie błędu z kroku na krok z przeciwnym znakiem, co na wykresie widoczne jest w postaci piły. Ta cecha algorytmu trapezów nazywa się „dzwonieniem” i powoduje że do rozwiązywania sztywnych równań różniczkowych jest nieprzydatny.

Rys. 4.10. Przebieg napięć na kondensatorach w wyniku symulacji z algorytmem Geara 2. rzędu.

W takich samych warunkach symulacji, algorytm Geara zachowuje się poprawnie. Powiększenie interesującego fragmentu wykresu uwidacznia niewielki błąd, który szybko jest tłumiony. Algorytmy Geara nadają się do rozwiązywania sztywnych równań różniczkowych.

4.5. Zadania dla studentów

5. Układy równań liniowych

Niniejszy rozdział poświęcono numerycznym technikom rozwiązywania równań liniowych.

5.1. Operacje na macierzach - rachunek macierzowy

Układ N równań liniowych zapisuje się

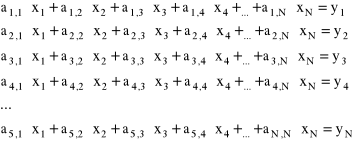
Wartości a_i,i są współczynnikami, x_i to niewiadome, a y_i to wartości stojące po prawej stronie równań.

Ten sam układ równań zapisuje się w postaci macierzowej

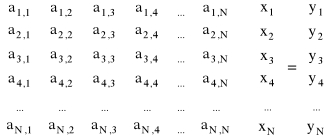
Macierz kwadratowa NxN zawierająca współczynniki nazywa się macierzą współczynników. Jest ona mnożona przez wektor niewiadomych X. Po prawej stronie równości stoi wektor Y nazywany wektorem wyrazów wolnych.

b) Wyznacznik macierzy

c) Uwarunkowanie macierzy

f) backward substitution, forward substitution - algorytmy redukcji wstecznej i w przód

d) Metoda eliminacji Gaussa-Jordana

e) Metoda Eliminacji Gaussa

f) Metoda LLT

g) Rozkład LU, metoda Crouta

g) Strategia wyboru elementu głównego

h) zadania dla studentów

Bibliografia

[B1] http://pl.wikipedia.org/wiki/Algorytm

[B2] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein "Wprowadzenie do algorytmów";WNT, wyd. VI 2004.

[D2] L. O. Chua, Pen Min Lin, „Komputerowa analiza układów elektronicznych”, WNT, Warszawa 1981, s. 428-435.

W języku C, wszystko, co jest różne od 0 jest prawdą, stąd warunek (r) należy interpretowac jako (r≠0).

lub zmniejszana.

Uwaga! Kolejne wartości k! wzrastają bardzo szybko i może dojść do przepełnienia. W praktyce należy stosować typ long.

W nowszych kompilatorach języka C++ zmienne typu int są czterobajtowe.

W metodzie Newtoda-Raphsona punkt startowy ma ogromne znaczenie. Im dokładniej przybliża miejsce zerowe, tym mniej iteracji trzeba przeprowadzić. W tym przypadku przyjęcie 3,5 nie jest zbyt dobrym przybliżeniem.

Ogólnie algorytmy DEI służą do rozwiązywania równań (układów równań) różniczkowych. Całkowanie numeryczne jest szczególnym przypadkiem, w którym funkcja podcałkowa jest znana.

Formalnie należałoby powiedzieć: wśród algorytmów wielokrokowych istnieją dwie metody prostokątów.

Jest to przyporządkowanie wynikające z klasyfikacji całej rodziny. Omawiane algorytmy formalnie należą także do algorytmów jednokrokowych gdyż s - krokowość wynosi 1.

Patrz definicja Bolzano - Cauchy'ego.

Z wykorzystaniem wartości z s poprzednich kroków.

W przypadku całkowania w przedziale <x_k .. x_k+2> z krokiem 2h wzór ten nosi nazwę wzoru Simpsona.

Sztywna (stiff) - nazwa pochodzi od sztywnych równań różniczkowych, których parametry (tzw. stałe czasowe) różnią się o wiele rzędów. Analiza stabilności algorytmów wykracza poza zakres materiału niniejszego opracowania.

43

---