Metody numeryczne

Bartłomiej Bułat, Michał Nowak, Konrad Malawski

12 grudnia 2009

Spis treści

1

Reprezentacja stało- i zmiennopozycyjna

2

1.1

Reprezentacja zmiennopozycyjna . . . . . . . . . . . . . . . . . .

2

1.2

Błąd reprezentacji zmiennoprzecinkowej . . . . . . . . . . . . . .

2

1.3

Reprezentacja stałopozycyjna . . . . . . . . . . . . . . . . . . . .

2

2

Uwarunkowanie zadania

2

3

Stabilność i poprawność numeryczna

3

3.1

Stabliność numeryczna algorytmów . . . . . . . . . . . . . . . . .

3

3.2

Poprawność numeryczna algorytmów . . . . . . . . . . . . . . . .

3

3.3

Złożoność obliczeniowa algorytmów . . . . . . . . . . . . . . . . .

3

4

Miejsca zerowe funkcji nieliniowych

3

4.1

Metoda bisekcji (połowienia przedziałów) . . . . . . . . . . . . .

3

4.2

Metoda Newtona (stycznych) . . . . . . . . . . . . . . . . . . . .

4

4.2.1

Szybkość zbieżności metody . . . . . . . . . . . . . . . . .

4

4.3

Metoda siecznych . . . . . . . . . . . . . . . . . . . . . . . . . . .

4

4.4

Metoda regula falsi (tylko na ćwiczeniach) . . . . . . . . . . . . .

4

5

Interpolacja

5

5.1

Interpolacja Lagrange’a . . . . . . . . . . . . . . . . . . . . . . .

5

5.2

Interpolacja Newtona . . . . . . . . . . . . . . . . . . . . . . . . .

6

5.3

Interpolacja Hermite’a . . . . . . . . . . . . . . . . . . . . . . . .

6

5.4

Efekt Rungego . . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

6

Interpolacja funkcjami sklejanymi

7

6.1

Interpolacja funkcjami sklejanymi 1 stopnia . . . . . . . . . . . .

8

6.2

Interpolacja funkcjami sklejanymi 3 stopnia . . . . . . . . . . . .

8

7

Licencja

9

1

1

Reprezentacja stało- i zmiennopozycyjna

1.1

Reprezentacja zmiennopozycyjna

Znormalizowana reprezentacja dziesiętna (x ∈ R, cecha: C ∈ Z, mantysa: 0,1 ·
|m| < 1, znak: s ∈ {¡1, 1}):

x

= s ¢ m ¢ 10

C

Znormalizowana reprezentacja dwójkowa (

1
2

· m < 1):

x

= s ¢ m ¢ 2

C

1.2

Błąd reprezentacji zmiennoprzecinkowej

Reprezentacja liczby rzeczywistej: rd(x) = s ¢ m

t

¢ 2

C

, gdzie t to ilość bitów

mantysy, zatem x = s ¢ m ¢ 2

C

jest dokładną liczbą x (m o nieskończonym

rozmiarze). Błąd wzgldędny wynosi:

¯

¯

¯

¯

x

¡ rd(x)

x

¯

¯

¯

¯

=

¯

¯

¯

¯

m

2

C

¡ m

t

2

C

m

2

C

¯

¯

¯

¯

·

1
2

¢ 2

1¡t

= 2

¡t

rd

(x) = x(1 ¡ ε), |ε| · 2

¡t

Liczba cyfr w mantysie określa dokładność reprezentacji, a liczba cyfr cechy -
zakres. C

max

= C

min

= 2

d

, gdzie d to liczba cyfr cechy, zatem reprezentoeane

są liczby:

1
2

2

C

min

· |x| · 2

C

max

Błąd niedomiaru pojawia się gdy C < C

min

, a błąd nadmiaru gdy C > C

max

.

1.3

Reprezentacja stałopozycyjna

Liczba reprezentowana jest na stałej ilości bitów, w wartość jej reprezentacji
wynosi w systemie dziesiętnym:

a

= s ¢

d¡1

X

i

=0

e

i

¢ 10

i

gdzie s ∈ {¡1, 1}, d to ilość cyfr i e

i

wartość i-tej cyfry. W systemie dwójkowym

wartość reprezentacji wynosi:

a

= s ¢

d¡1

X

i

=0

e

i

¢ 2

i

2

Uwarunkowanie zadania

Uwarunkowanie zadania nie zależy od metod jego rozwiązania. Jeśli mamy
dane: d

0

, d

1

, . . . , d

n

∈ R i zamiast ich wartości dysponujemy ich reprezenta-

cjami rd(d

i

) = d

i

(1 + ε

i

), gdzie |ε

i

| · 2

¡t

, to ta niewielka zmiana może spo-

wodować duże zmiany względne rozwiązania. Jeżeli niewielkie względne zmiany
danych powodują duże względne zmiany jego rozwiązania to zadanie nazywamy
źle uwarunkowanym. Wielkości charakteryzujące wpływ zaburzeń danych na
zaburzenia rozwiązania nazywamy wskaźnikami uwarunkowania zadania.

2

3

Stabilność i poprawność numeryczna

3.1

Stabliność numeryczna algorytmów

Definicja 1.

Stabilność numeryczna algorytmów

Mamy dane:
D

- zbiór danych

a

= (a

1

, a

2

, . . . , a

k

) - wektor danych

W

= (W

1

, W

2

, . . . , W

k

) - wektor wyniku

W

= W (a) – algorytm idealny

W

′

= W N (a, ε) – algorytm numeryczny (W

′

- wynik numeryczny)

DN

(ε) - zbiór danych, dla których określony jest algorytm W N (a, ε).

Mówimy, że algorytm obliczeniowy jest numerycznie stabilny, jeśli:

∀a

0

∈ D ∃ε

0

: ∀ε < ε

0

a

0

∈ DN (ε) ∧ lim

ε→0

W N

(a

0

, ε

) = W (a

0

)

czyli algorytm jest numerycznie stabilny wtedy, gdy zwiększając dokładność obli-
czeń można wyznaczyć (z dowolną dokładnością) dowolne istniejące rozwiązanie
zadania.

3.2

Poprawność numeryczna algorytmów

Algorytmy poprawne numerycznie są podzbiorem algorytmów numerycznie sta-
bilnych.

Definicja 2.

Algorytm numerycznie poprawny.

Za numerycznie najwyższej jakości uznajemy takie algorytmy, dla których ob-
liczone rozwiązanie jest nieco zaburzonym rozwiązaniem (dokładnym) zadania
o nieco zaburzonych danych. Algorytmy spełniające ten postulat nazywamy nu-
merycznie poprawnymi.

3.3

Złożoność obliczeniowa algorytmów

Definicja 3.

Złożoność obliczeniowa algorytmu.

Złożoność obliczeniowa to funkcja określająca maksymalną ilość operacji, które
należy wykonać, aby obliczyć wynik za pomocą danego algorytmu.

4

Miejsca zerowe funkcji nieliniowych

4.1

Metoda bisekcji (połowienia przedziałów)

Warunkami zbieżności tej metody jest to, aby funkcja posiadała dokładnie jeden
pierwiastek w przedziale izolacji, była w num ciągła, a na jego końcach miała
przeciwne znaki.
Algorytm wyznaczania kolejnego przybliżenia:

1. Wyznaczamy środek przedziału: m

n

=

a

n¡1

+b

n¡1

2

, dla n = 1, 2, . . ..

2. Jeśli m

n

jest wystarczającym przybliżeniem, koniec.

3. Jeśli f (a

n¡1

) ¢ f (m

n

) < 0 to a

n

= a

n¡1

, a b

n

= m

n

.

4. Jeśli f (b

n¡1

) ¢ f (m

n

) < 0 to a

n

= m

n

, a b

n

= b

n¡1

.

3

4.2

Metoda Newtona (stycznych)

Warunkami zbieżności tej metody jest to, aby funkcja posiadała dokładnie jeden
pierwiastek w przedziale izolacji, była w num ciągła, a na jego końcach miała
przeciwne znaki. Funkcja musi być klasy C

2

oraz pierwsza i druga pochodna

muszą mieć stały znak w przedziale.
Algorytm wyznaczania kolejnego przybliżenia:

1. Zerowe przybliżenie wyznaczene jest z warunku: f (a) ¢ f

′′

(a) > 0. Jeśli

jest on prawdziwy x

0

= a, jeśli nie to x

0

= b.

2. Kolejne przybliżenie wyznaczamy ze wzoru: x

n

= x

n¡1

¡

f

(x

n¡1

)

f

′

(x

n¡1

)

.

3. Jeśli przybliżenie nas satysfakcjonuje kończymy obliczenia.

4.2.1

Szybkość zbieżności metody

Definicja 4.

Szybkość zbieżności metody Newtona.

Niech x

0

, x

1

, x

2

, . . .

będzie ciągiem zbieżnym do

; ε

n

= x

n

¡

.

Jeśli istnieją takie dwie liczby p, c ,gdzie c 6= 0, że:

lim

n→inf

sup

¯

¯

¯

¯

ε

n

+1

ε

p

n

¯

¯

¯

¯

= c

p

nazywamy wykładnikiem zbieżności ciągu

c

– stałą asymptotyczną błędu.

Dla p = 1, 2, 3 mówimy o zbieżności odpowiednio, liniowej, kwadratowej i sze-
ściennej.

4.3

Metoda siecznych

Warunki zbieżności takie jak w metodzie Newtona.
Algorytm wyznaczania kolejnych przyliżeń:

1. Pierwsze dwa przybliżenia wyzbaczamy z krańców przedziału: x

0

= a i

x

1

= b.

2. Kolejne przybliżenie wyznaczamy ze wzoru: x

n

= x

n¡1

¡

f

(x

n¡1

)¢(x

n¡1

¡x

n¡2

)

f

(x

n¡1

)¡f (x

n¡2

)

,

dla n = 2, 3, 4, . . ..

3. Jeśli przybliżenie nas satysfakcjonuje kończymy obliczenia.

4.4

Metoda regula falsi (tylko na ćwiczeniach)

Warunki zbieżności takie jak w metodzie Newtona.
Algorytm wyznaczania kolejnych przyliżeń:

1. Pierwsze dwa przybliżenia wyzbaczamy ze wzoru: x

0

=

a¢f (b)¡b¢f (a)

f

(b)¡f (a)

2. Wyznaczamy punkt stały metody z warunku: f (a)f (x) < 0, jeśli jest on

prawdziwy to c = a, w przeciwnym przypadku c = b.

3. Kolejne przybliżenie wyznaczamy ze wzoru: x

n

=

x

n¡1

f

(c)¡cf (x

n¡1

)

f

(c)¡f (x

n¡1

)

, dla

n

= 1, 2, 3, 4, . . ..

4. Jeśli przybliżenie nas satysfakcjonuje kończymy obliczenia.

4

5

Interpolacja

W przedziale [a, b] danych jest n + 1 różnych punktów x

0

, x

1

, ..., x

n

(węzły in-

terpolacji) oraz wartości funkcji y = f (x) w tych punktach f (x

0

) = y

0

, f

(x

1

) =

y

1

, ..., f

(x

n

) = y

n

. Zadaniem interpolacji jest znalezienie F (x) , która w węzłach

interpolacyjnych ma te same wartości co f (x) i przybliża f (x) w punktach po-
średnich.

Twierdzenie 1.

O istnieniu dokładnie jednego wielomianu interpolacyjnego.

Istnieje dokładnie jeden wielomian interpolacyjny stopnia co najwyżej n, (n >
0), który w punktach x

0

, x

1

, ..., x

n

przyjmuje wartości y

0

, y

1

, ..., y

n

.

Dowód.

W

n

= a

0

+ a

1

x

+ a

2

x

2

+ ... + a

n

x

n

(1)

korzystając z n + 1 (par) wartości (x

i

, y

(x

i

)) mamy układ równań:














a

0

+ a

1

x

0

+ a

2

x

2

0

+ ¢ ¢ ¢ + a

n

x

n

0

= y

0

a

0

+ a

1

x

1

+ a

2

x

2

1

+ ¢ ¢ ¢ + a

n

x

n

1

= y

1

¢ ¢ ¢

a

0

+ a

1

x

n

+ a

2

x

n

2

+ ¢ ¢ ¢ + a

n

x

n

n

= y

n

(2)

z n + 1 niewiadomymi a

0

, a

1

, ..., a

n

D

= detA =

1

x

0

x

2

0

...

x

n

0

1

x

1

x

2

1

...

x

n

1

...

...

...

...

...

1

x

n

x

2

n

...

x

n

n

(3)

Wyznacznik Vandermande’a 6= 0, gdy x

i

6= x

j

dla i 6= j

a

i

=

1

D

n

X

j

=0

f

(x

j

)D

ij

(4)

4 dopełnienie algebraiczne elementów i–tej kolumny, j–tego wiersza

5.1

Interpolacja Lagrange’a

Wzory ostateczne:

L

n

(x) = y

0

(x¡x

1

)¢(x¡x

2

)¢...¢(x¡x

n

)

(x

0

¡x

1

)¢(x

0

¡x

2

)¢...¢(x

0

¡x

n

)

+ y

1

(x¡x

0

)¢(x¡x

2

)¢...¢(x¡x

n

)

(x

1

¡x

0

)¢(x

1

¡x

2

)¢...¢(x

1

¡x

n

)

+ . . .

+y

n

(x¡x

0

)¢(x¡x

1

)¢...¢(x¡x

n¡1

)

(x

n

¡x

0

)¢(x

n

¡x

1

)¢...¢(x

n

¡x

n¡1

)

Oznaczamy: W

n

+1

(x) = (x ¡ x

0

) ¢ (x ¡ x

1

) ¢ . . . ¢ (x ¡ x

n

)

|

{z

}

n

+1czynnikow

L

n

(x) =

n

X

j

=0

y

j

¢

W

n

+1

(x)

(x ¡ x

j

) ¢

½

W

n1

(x)

(x¡x

j

)

¯

¯

¯

x

=x

j

¾

jest to wzór interpolacyjny Lagrange’a.

5

5.2

Interpolacja Newtona

Aby biegle korzystaż z wzoru interpolacyjnego Newtona, przypomnijmy sobie
jak wygląda iloraz różnicowy:

f

[x

i

, x

i

+1

] =

f

[x

i

+1

, x

i

+1

] ¡ f [x

i

, x

i

]

x

i

+1

¡ x

i

W przypadku ogólnym korzystać będziemy z jego zfediniowanej rekurencyj-

nie postaci:

f

[x

i

, . . . , x

i

+j+1

] =

f

[x

i

+1

, . . . , x

i

+j+1

] ¡ f [x

i

, . . . , x

i

+j

]

x

i

+j+1

¡ x

i

Wzór interpolacyjny Newtona:

w

(x) =

n

X

i

=0

a

i

i¡1

Y

j

=0

(x ¡ x

j

)

(5)

gdzie a

i

oznacza ity iloraz różnicowy (patrz poniższy algorytm).

Algorytm "wizualnego"ułatwienia sobie liczenia ilorazów różnicowych wyż-

szych rzędów:

1. Stwórz tabelę o 2 kolumnach i tylu wierszach ile masz punktów interpolacji

2. Pierwszą kolumnę wypełnij wartościami x tych punktów a drugą f(x)

3. Każdą kolejną kolumnę utwórz poprzez obliczenie ilorazu różnicowego z

„2 poprzednich“ oraz odpowiadających im wartości x z pierwszej kolumny

4. Interesujące nas do wzoru interpolującego newtona ilorazy są pierwszymi

elementami w poszczególnych kolumnach

Poniżej przykżadowa tabelka ilorazów różnicowych:

x

f

(x)

a

1

a

2

a

3

a

4

0

1

1

¡

2
3

2
3

¡

2
9

2

3

¡1

2

¡

2
3

3

2

3

¡

2
3

4

5

1

6

7

Rozpisany wzór Newtona dla funkcji przedstawionej w powyższej tabeli:

w

(x) = 1 + 1(x ¡ 0) ¡

2
3

(x ¡ 0)(x ¡ 2) +

2
3

(x ¡ 0)(x ¡ 2)(x ¡ 3) ¡

2
9

(x ¡ 0)(x ¡ 2)(x ¡ 3)(x ¡ 4) =

¡

2
9

x

4

+

8
3

x

3

¡

88

9

x

2

+

35

3

x

+ 1

5.3

Interpolacja Hermite’a

Interpolacja Hermita poza wartościami funkcji korzysta również z pierwszej po-
chodnej interpolowanej funkcji, umożliwia zatem uzyskanie dokładniejszego od-
wzorowania.

H

2n+1

(x) =

n

X

j

=0

f

(x

j

)H

n,j

x

+

n

X

j

=0

f

′

(x

j

)Hd

n,j

x

6

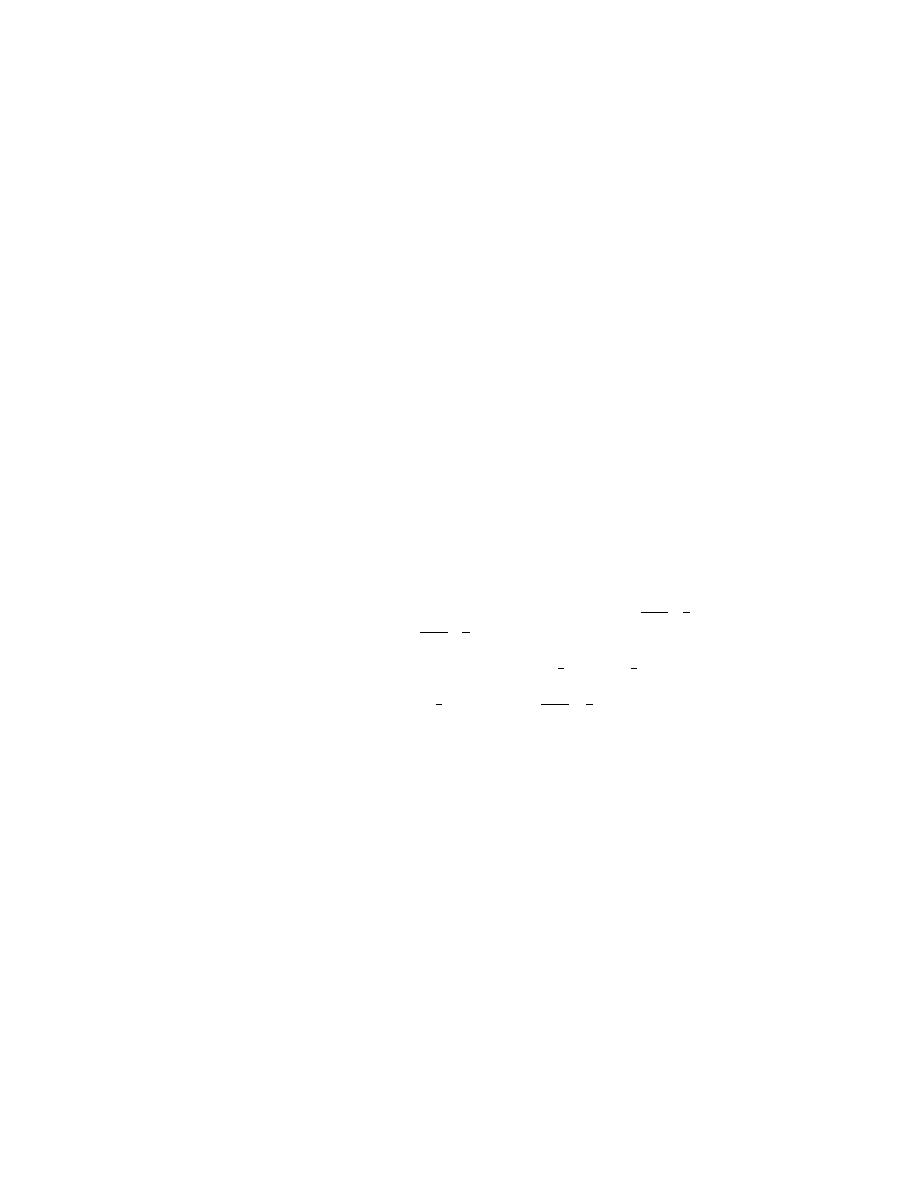
gdzie

H

n,j

(x) = (1 ¡ 2(x ¡ x

j

)L

′

n,j

(x

j

))L

2

n,j

(x)

oraz

Hd

n,j

(x) = (x ¡ x

j

)L

2

n,j

(x)

a L

n,j

jest oczywiście jtym współczynnikiem wielomianu Lagrange’a stopnia

n

.

Twierdzenie 2.

Zadanie interpolacyjne Hermite’a ma jednoznaczne rozwiąza-

nie.

5.4

Efekt Rungego

Przy równoodległych węzłach w środku przedziału są małe błędy, ale na krań-
cach gwałtownie wzrastają i funkcja się „rozjeżdża”.

Do optymalnego doboru węzłów interpolacji słyży wielomian Czybyszewa:

T

n

(x) = cos(arccos(x))

1. Rekurencyjne obliczanie wielomianu:

T

0

(x) = 1

T

1

(x) = x = x ¢ T

0

(x)

T

n

+1

(x) = 2 ¢ x ¢ T

n

¡ T

n¡1

dla n ¸ 1

2) T

n

(x) jest równoważny pewnemu wielomianowi algebraicznemu stopnia

n

określonego w przedziale [¡1, 1] 3) Współczynnik wiodący (przy najwyższej

potędze) T

n

wynosi:

½

2

n¡1

dlan

¸ 1

1

dlan

= 1

4) t

n

ma n zer w [¡1, 1] jednokrotnych, rzeczywistych: x

k

= cos

¡

2k+1

n

¢

2

¢

,

dla k = 0, 1, ..., n ¡ 1 lub x

k

= cos

¡

2k¡1

n

¢

2

¢

, dla k = 1, 2, ..., n

Przeskalowanie z [¡1, 1] do [a, b]: Dowolną f (t) dla t ∈ [a, b] można prze-

skalować, aby była określona w [¡1, 1] i odwrotnie: t =

1
2

(a + b) +

1
2

(b ¡ a) ¢ x

t

∈ [a, b] ⇔ x ∈ [¡1, 1] przeskalowanie nie zmienia błędu interpolacji.

Optymalne węzły w [a, b]: t

k

=

1
2

£

(b ¡ a) ¢ cos

¡

2k+1

n

¢

2

¢

+ (b + a)

¤

dla

k

= 0, 1, ..., n ¡ 1

6

Interpolacja funkcjami sklejanymi

Funkcje sklejane brzmią strasznie ale są bardzo przyjemne, inna nazwa na nie
to z ang. spline, a spalszczamy je (kto wie czy poprawnie) jako śplajny"...

Ogólny pomysł jest następujący: Zamiast 1 funkcji interpolującej, chcemy

uzyskać tyle funkcji ile jest przedziałów interpolacji. Na przykład dla 3 węzłów
interpolujących, uzyskamy 2 splajny, które gdy je śkleimy"utworzą naszą funkcję
interpolującą.

Zalety splajnów:

² Szybciej się liczy spline niż zwyczajne interpolacje wielomianowe, powo-

dem jest stopień wielomianów na których pracujemy (przy spline jest za-
zwyczaj bardzo niski, popularna jest wartość 3)

² Są odporne na efekt Rungego (?!?!)

7

6.1

Interpolacja funkcjami sklejanymi 1 stopnia

Inaczej nazywama: liniowa. Liniowa dlatego że spline 1 stopnia, to nic innego
niż funkcja liniowa. A całą interpolację można przedstawić jako "połącz punkty
interpolacji prostymi odcinkami". Funkcja otrzymana w wyniku tej interpolacji
będzie bardzo kanciasta, ale również bardzo szybko ją obliczymy. Wzór na kty
spline wygląda następująco:

s

k

(x) = y

k

+

y

k

+1

¡ y

k

k

+1

¡ x

k

(x ¡ x

k

)

Funkcję rzeczywistą nazywamy spline stopnia m z węzłami s = a = x

0

, x

1

¢ ¢ ¢ x

N

=

b

jeśli

1. w każdym przedziale (x

i¡1

, x

i

)dlai = 0, 1, ¢ ¢ ¢ , N + 1 s jest wielomianem

stopnia nie wyższego niż m

2. s i jej pochodne rzędu 1, 2, ¢ ¢ ¢ , m ¡ 1 są ciągłe na całej osi rzeczywistej;

innymi słowy s ∈ C

m¡1

Definicja 5.

Funkcję sklejaną stopnia 2m ¡ 1 nazywamy naturalną jeśli w

przedziałach (¡∞, x

0

), (x

N

,

∞) jest wielomianem stopnia m ¡ 1

Twierdzenie 3.

Interpolacja naturalną funkcją sklejaną jest ńajgładszą"funkcją

interpolującą punktu (x, y

i

)

6.2

Interpolacja funkcjami sklejanymi 3 stopnia

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Suspendisse aliquam
augue vitae leo ultricies imperdiet. Morbi at nibh nunc, quis suscipit est. Class
aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos hime-
naeos. Donec sit amet gravida lectus. Nam tincidunt urna velit. Cras sagittis
enim gravida turpis volutpat vel tempus nisi imperdiet. Donec risus diam,
pellentesque id vulputate eu, dignissim non leo. Nullam aliquet odio eu enim
egestas vehicula. Integer commodo porta tortor sit amet accumsan. Curabitur
ac enim id metus malesuada tempor eu id turpis. Aenean magna nibh, ullam-
corper in ornare at, pellentesque nec sapien. Proin tincidunt sapien scelerisque
nulla viverra molestie. Aliquam et massa in sem auctor molestie eget sit amet
mauris. Morbi mi velit, adipiscing sed condimentum at, iaculis ut neque. In
non ultrices diam.

8

7

Licencja

Ten utwór objęty jest licencją Creative Commons:

² Uznanie autorstwa

² Użycie niekomercyjne

² Na tych samych warunkach

3.0 Polska.

Aby zobaczyć kopię niniejszej licencji przejdź na stronę http://creativecommons.org/licenses/by-

nc-sa/3.0/pl/ lub napisz do Creative Commons, 171 Second Street, Suite 300,
San Francisco, California 94105, USA.

9