Artur Czekalski; Zadanie z MEN421; 25-XII-2001

METODA BAIRSTOWA

wykorzystywana jest do znalezienia przybliżonych wartości pierwiastków zespolonych wielomianu f(x)=a_nxⁿ+...+a₀ o współczynnikach rzeczywistch.

Metoda ta unika arytmetyki zespolonej. Opiera się na twierdzeniu:

* TW.

Zera rzeczywistego wielomianu kwadratowego x²-px-r są zerami danego wielomianu rzezywistego f(x) wtedy i tylko wtedy, gdy wielomian f(x) można podzielić bez reszty przez x²-px-r.

* Zatem gdy znajdziemy dzielniki kwadratowe wielomianu f(x) będziemy mogli poznać jego zera.

Rozkład na dzielniki kwadratowe (z jednym rzeczywistym liniowym czynnikiem, jeśli stopień n jest nieparzysty) istnieje, gdyż każdemu zespolonemu zeru α odpowiada zero α¯­-sprzężone wielomianu f, a dzielnik (x-α)(x-α¯) ma współczynniki rzeczywiste. (Niech α=a+bi, wtedy (x-α)(x-α¯)=x² - 2ax + a²+b ).

*Zatem szukamy takich p,r aby x²-px-r | f(x).

Niech m(x) = m(x;p,r) = x²-px-r będzie dowolnym trójmianem kwadratowym o współczynnikach rzeczywistych. Dzieląc wielomian f przez m otrzymamy iloraz Q i resztę, tzn:

f(x)= m(x,p,r) * Q(x;p,r) + q₁(p,r) + q₀(p,r);

Wtedy trójmian m^*(x;p,r) jest dzielnikiem f wtedy i tylko wtedy, gdy q₁(p^*,r^*) = q₀(p^*,r^*) = 0.

*Zatem chcąc znaleźć takie p^*, r^* musimy rozwiązać układ dwóch równań nieliniowych o dwóch niewiadomych.

q₀(p,r)=0

q₁(p,r)=0

Medoda Bairstowa polega na zastosowaniu dwuwymiarowej metody Newtona do tego układu. Dla danego przybliżenia początkowego [p₀,r₀] wektora [p^*,r^*] konstrujemy ciąg {[p_k,r_k]} określony zależnościami:

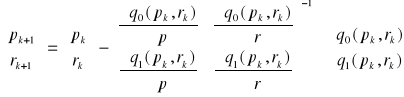
(1)

Obliczenie w każdym kroku k, współczynników q₀ i q₁ wymaga jedynie podzielenia wielomianu f przez m_k(x)=x²-p_kx-r_k. Okazuje się, że w sposób analogiczny można wyznaczyć pochodne występujące w powyższej formule.

Różniczkując równość (1) kolejno względem p i r otrzymamy dwie następne tożsamości ze względu na x:

Wielomiany dQ/dp oraz dQ/dr są ilorazami stopni n-3 i n-4 powstałymi z podzielenia x*Q(x) i Q(x) przez trójmian m, a poszukiwane pochodne - współczynnikami reszt z tych dzieleń.

Iteracja wygląda więc następująco:

do

{PodzielWiel(Stopien, A, p,r, Q, Reszta); //dzielenie f(x)/m

if (fabs(Reszta[1])<eps && fabs(Reszta[0])<eps) break; //A dzieli się przez trójmian (p,r) więc kończ iterację

PodzielWiel(Stopien-2, Q, p,r, W, dqdr); //dzielenie Q(x)/m

for (i=Stopien-2;i>=0;i--) Q[i+1]=Q[i]; //mnożenie Q(x) przez x

Q[0]=0;

PodzielWiel(Stopien-1, Q, p,r, W, dqdp); //dzielenie Q(x)*x/m

q=LiczMOdwrotna(dqdp[0],dqdr[0],dqdp[1],dqdr[1],a,b,c,d); //wyliczenie odwrotności macierzy

p = p - (a*Reszta[0] + b*Reszta[1]); //obliczenie nowego wektora [p,r]

r = r - (c*Reszta[0] + d*Reszta[1]);

} while (1);

Po znalezieniu takich p^*, r^* dzielimy wielomian f przez m^* i jeżeli stopień f=f/m^* jest >= 2 znów szukamy kolejnego dzielnika m^*.

Oczywiście znalezione p, r są przybliżeniami p^*, r^* na tyle dobrymi, że q₁(p,r) <eps i q₀(p,r) <eps dla zadanej wartości eps (która jest odpowiednio mała)

* Wykorzystywane funkcje:

int Bairstow(int Stopien,double const *tabA, double *tabP,double *tabR, double eps, double p_,double r_)

Stopien - stopien wielomianu

tabA - tablica współczynników wielomianu

tabP, tabR - tablice współczynników (p,r) trójmianów kwadratowych jako wynik

eps - dokładność pierwiastków

p,r - początkowe przybliżenie współczynników trójmianu

int PodzielWiel(int Stopien,double const *A, double p,double r, double *Q,double *R)

Dzieli wielomian o współczynnikach z tablicy A przez trójmian x²-px-r. Wynik zapisany w tablicy Q, reszta w tablicy R

Prosty algorytm o złożoności: O(Stopień)

int LiczMOdwrotna(double x,double y,double w,double z, //dana macierz 2x2

double &a,double &b,double &c,double &d) //wynik

Tylko 4 podstawienia.

---