POLITECHNIKA WROCŁAWSKA ZAKŁAD AUTOMATYKI i STEROWANIA w ENERGETYCE		Skład grupy: 1. Anna Knap 170739	Wydział: Elektryczny Rok studiów: 3 Rok Akademicki : 2010/2011 Grupa: Termin: Wtorek, 07:30
METODY NUMERYCZNE
Data wykonania ćwiczenia: 31.05.2011	Nr ćwiczenia: 11 Temat: Zadania na zaliczenie projektu.
Data oddania sprawozdania: 7.06.2011
Prowadzący: Mgr inż. Łukasz Staszewski

Cel ćwiczenia: Rozwiązanie dwóch z zadań podanych przez prowadzącego.

Przebieg ćwiczenia:

Dwa wybrane przeze mnie zadania:

Zad. 6 Całkowanie

Zadana całka i jej obliczenie analityczne:

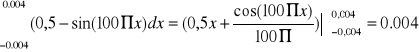
Tabela 1. Wyliczenie całki różnymi metodami

	Metoda
tp	Eulera jawna	Eulera niejawna	Trapezowa	Simpsona	Analityczna	Wolfram
0.0001	0.004095105651630	0.003904894348370	0.004	0.00395	0.004	0.004

Wykres 1. Graficzne porównanie metod całkowania

Zad. 7. Układ równań

Rozwiązanie układu równań różniczkowych z użyciem metody Runie-Kutty 4-rzędu.

Rozwiązanie w przedziale: t=0..10

Krok całkowania: h=0.1, h=0.5oraz h=1.0

Warunki początkowe: y₁(0)=1, y₂(0)=2

Układ równań: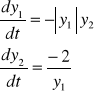

Wykres 1 Porównanie całkowania metodą Runge-Kutty'ego dla kroków całkowania: 0.1 oraz 0.5

Wykres 3 Całkowanie metodą Runge-Kutty'ego dla kroku całkowania: 0.999

Wnioski:

• Całkowanie metodą trapezową jest najdokładniejsze, bo łączy w sobie zarówno metodę jawną jak i niejawną Eulera i jedynie ona dała wynik identyczny z wartością wyliczoną analitycznie.

• Niestety metodę trapezową można skutecznie używać jedynie przy obliczaniu całki podanej jawnym równaniem

• Metoda Simsona jest najmniej wydajna z metod, przy znacznym zmniejszeniu kroku całkowania, przeliczenie tą metodą trwa najdłużej

• Przy wyliczaniu układu równań niemożliwe okazało się przedstawienie charakterystyk dla podanych kroków całkowania na jednym wykresie, więc musiałam rozbić je na 2 wykresy

• Nie wiem czemu przy ustawieniu kroku całkowania 1 program nie chciał działać, więc zmniejszyłam krok na 0.999 i dla niego wykreśliłam charakterystyki. Myślę, że przy takiej dużej zmianie kroku całkowania (z 0,5 na 1) błąd rzędu 0.001 nie będzie miał dużego znaczenia.

• Łatwo zauważyć, zwłaszcza dla funkcji y₁, że krok całkowania ma znaczący wpływ - im mniejszy, tym dokładniejszą charakterystykę otrzymujemy, dla dużego kroku nasza charakterystyka robi się liniowa w pewnych zakresach.

3

---