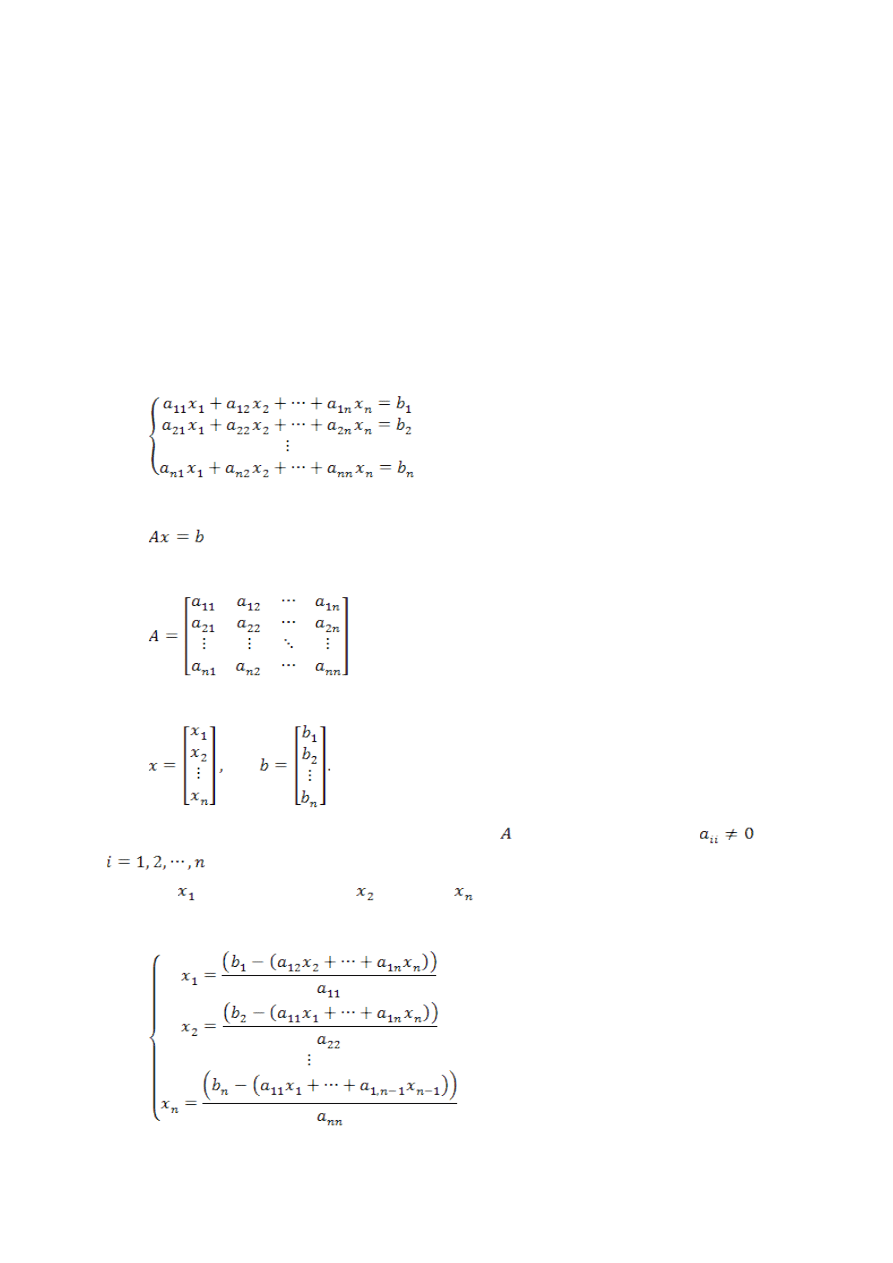
I

TERACYJNE

METODY

ROZWIĄZYWANIA

UKŁADÓW

RÓWNAŃ

LINIOWYCH

1.1. M

ETODA

ITERACJI

PROSTYCH

Ogólny schemat obliczeń iteracyjnych przedstawia metoda iteracji prostych. Za jej

pomocą można rozwiązać układ równań liniowych (o n niewiadomych) (1.1.1)

Układ ten można zapisać w postaci

przyjmując, że

oraz

Przy założeniu, że elementy główne macierzy są różne od zera (czyli

dla

), należy przekształcić układ 1.1.1 w taki sposób, aby wyznaczyć z pierwszego

równania , z drugiego równania , itd. aż do .

Dostajemy

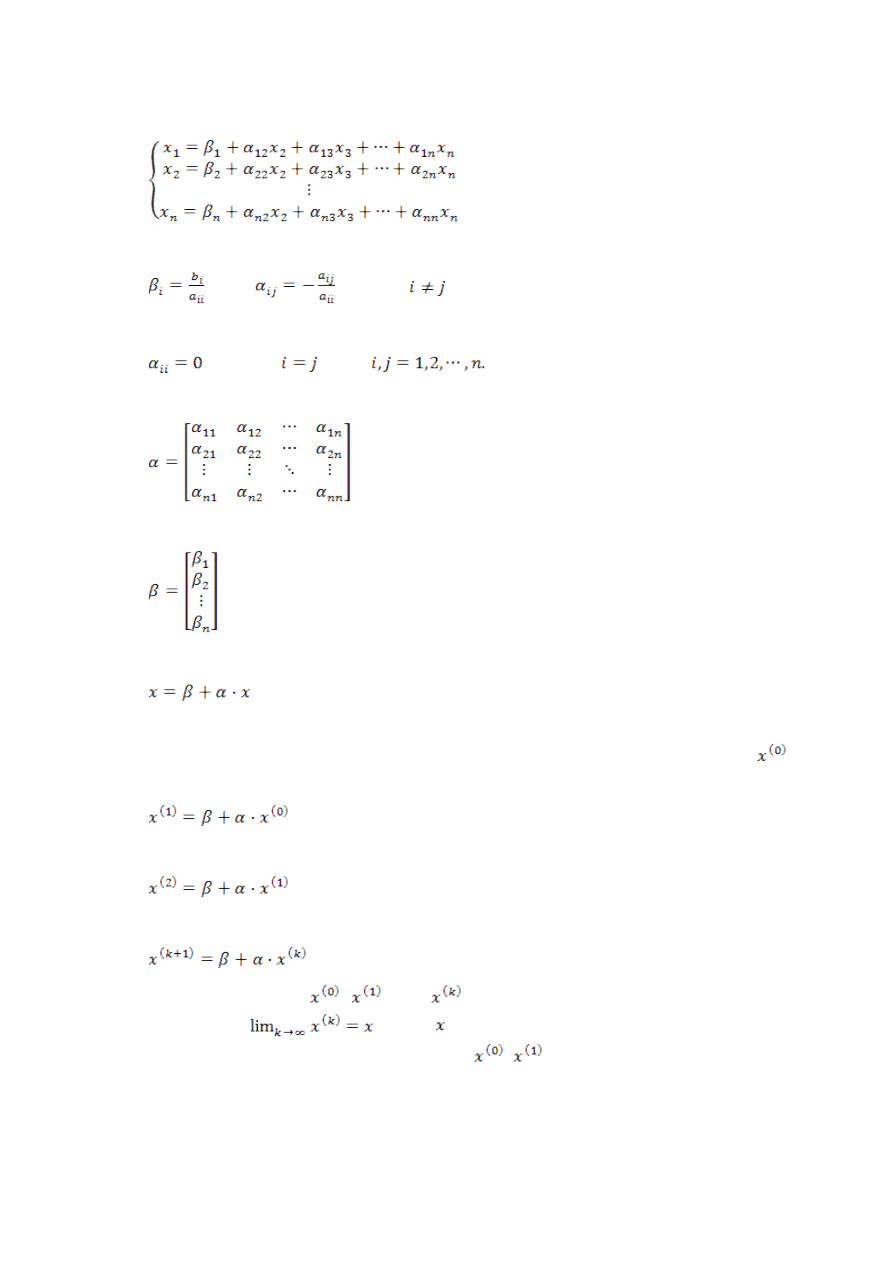
Otrzymany układ można zapisać równoważnie w postaci (1.1.2)

gdzie:

,

dla

oraz

dla

,

Przyjmując

oraz

układ 1.1.2 można zapisać w postaci macierzowej jako

Otrzymaną równość wykorzystuje się do uzyskania kolejnych przybliżeń rozwiązania

układu. W tym celu, jako rozwiązanie początkowe, obiera się dowolny wektor

(np. wektor zerowy) i oblicza się kolejne iteracje

(przybliżenie pierwsze),

(przybliżenie drugie) itd. Stąd ogólny wzór iteracyjny (1.1.3)

Kolejne przybliżenia

,

, … ,

, … utworzą ciąg wektorów. Jeżeli istnieje

granica tego ciągu

, wtedy jest rozwiązaniem układu równań liniowych.

Aby powyższa granica istniała, to ciąg wektorów

,

, … musi być ciągiem zbieżnym.

Zbieżność tego ciągu jest równoważna zbieżności metody iteracyjnej.

2

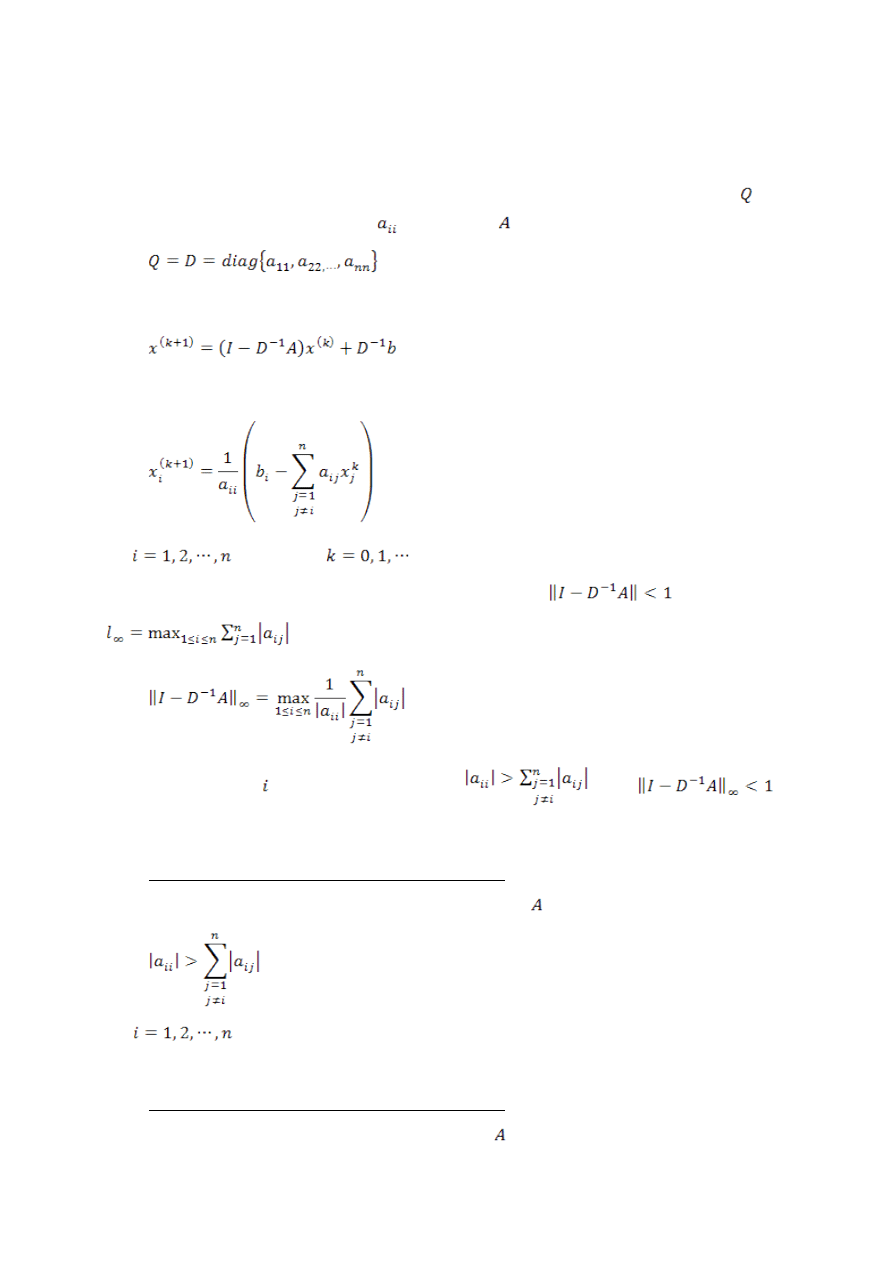
1.3. M

ETODA

J

ACOBIEGO

Jedną z metod iteracyjnych jest metoda Jacobiego [1, 4, 7, 8]. Jej macierz jest

macierzą przekątniową o elementach

takich, jak w , czyli

Wtedy proces iteracyjny zapisuje się jako

Inaczej można go zapisać w postaci

dla

oraz iteracji

.

Metoda ta będzie zbieżna wtedy i tylko wtedy, gdy

. Biorąc normę

Jeżeli dla wszystkich spełniona jest nierówność

, to

.

Zatem prawdziwe są twierdzenia:

Twierdzenie 3

a (Mocne kryterium sumy wierszy)

Metoda Jacobiego jest zbieżna dla wszystkich macierzy spełniających warunek (1.3.1):

dla

.

Twierdzenie 3b (Mocne kryterium sumy kolumn)

Metoda Jacobiego zbiega dla wszystkich macierzy spełniających warunek (1.3.2):

3

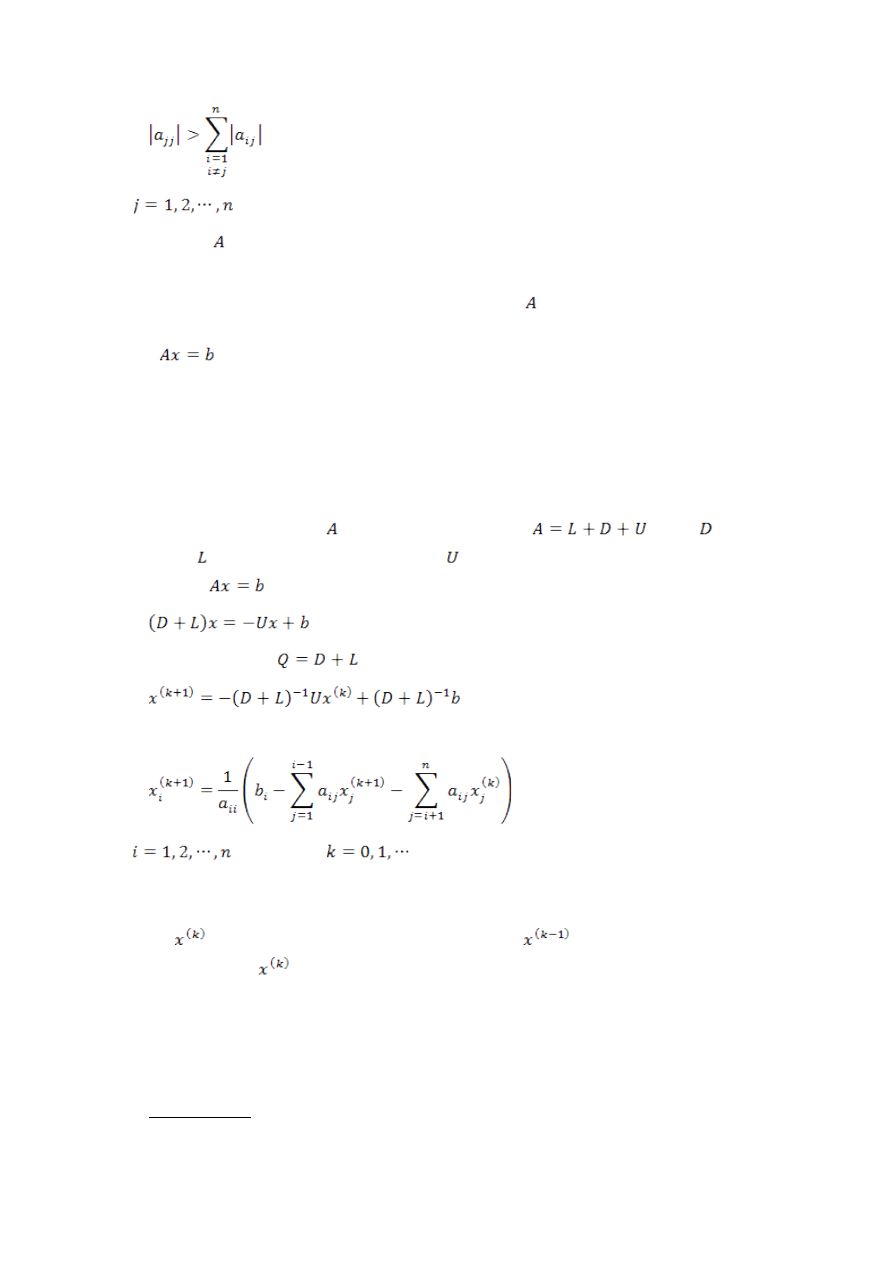
dla

.

Macierz spełniająca warunek 1.3.1 (1.3.2) nazywana jest macierzą ściśle diagonalnie

dominującą według wierszy (według kolumn).

Równoważnie można powiedzieć, że jeśli macierz jest dominująca przekątniowo, to

dla dowolnego wektora początkowego metoda Jacobiego tworzy ciąg zbieżny do rozwiązania
układu

.

1.4. M

ETODA

G

AUSSA

-S

EIDLA

W metodzie tej macierz przedstawia się w postaci

, gdzie - macierz

diagonalna, - macierz trójkątna dolna, zaś - macierz trójkątna górna [1, 7, 8]. Wtedy
układ równań

można przedstawić w postaci

Zatem dla wzoru 1.2.1

. Dlatego proces iteracyjny można zapisać w postaci

Równoważna postać tego procesu to

dla

oraz iteracji

.

Zapis ten dobrze pokazuje różnicę pomiędzy tą metodą iteracyjną a metodą Jacobiego.

Widać, że metoda Gaussa-Seidla, wyznaczając w jednym kroku iteracyjnym kolejne elementy
wektora

, korzysta zarówno z wartości wektora

jak i z wyznaczonych już

elementów wektora

. W metodzie Jacobiego natomiast nowe przybliżenia składowych

rozwiązania wykorzystywane są dopiero w kolejnej iteracji, dzięki czemu można je obliczać
jednocześnie.

Kryterium zbieżności metody Gaussa-Seidla jest takie samo jak dla metody Jacobiego,

co pokazuje poniższe twierdzenie:

Twierdzenie 4

4

Jeśli macierz jest dominująca przekątniowo, to metoda Gaussa-Seidla jest zbieżna

dla dowolnego wektora początkowego.

5