Ćwiczenie 65
Wyznaczanie pojemności kondensatora metodą drgań relaksacyjnych
Przyrządy:
Zasilacz prądu stałego (300V/30mA), neonówka, kondensator dekadowy: C= 0÷10 μF, opornik dekadowy: R= 0÷10 MΩ (schemat połączeń tych elementów układu pomiarowego przedstawia rys.1), stoper dwa kondensatory o nieznanej pojemności C1, C2 i przewody.
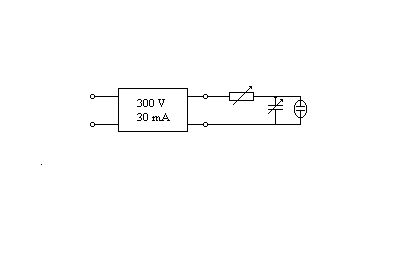
Rys.1.
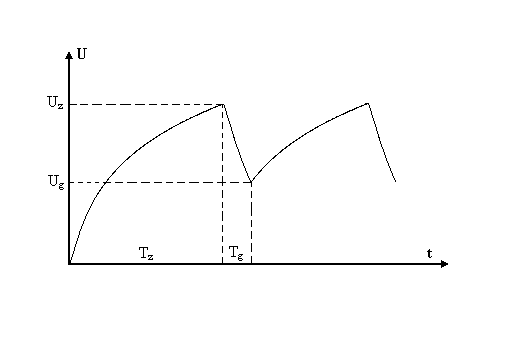
Rys.2.
Okres drgań relaksacyjnych T w obwodzie przedstawionym na rys.1 wyraża się wzorem:
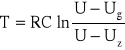
(1)
gdzie: Uz - napięcie zapłonu neonówki
Ug - napięcie gaśnięcia neonówki
Oznaczając przez K logarytm ilorazu różnicy napięć: 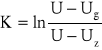
oraz uwzględniając wpływ oporności neonówki w stanie zjonizowanym na relacje między czasem ładowania i rozładowania kondensatora równ.1 można zapisać ogólnie w postaci:
![]()
(2)
Stała czasowa t0 w równaniu (2) jest bliska zeru w przypadku gdy czas rozładowania (Tg na rys.2) kondensatora jest bardzo mały w porównaniu z czasem jego ładowania (Tz) tj. gdy oporność neonówki w stanie zjonizowanym jest bardzo mała. W przeciwnym razie następuje częściowe doładowywanie kondensatora w trakcie jego rozładowywania się poprzez neonówkę i okres drgań relaksacyjnych zwiększa się o pewną stałą wartość t0.
Równanie 2 jest liniową funkcją iloczynu RC, której współczynnik nachylenia jest równy stałej K, a wyraz wolny stalej czasowej t0. Wartości stałych K i t0 można wyznaczyć znajdując parametry prostej korelacji dopasowanej do wyznaczonego doświadczalnie wykresu funkcji T=f(RC). Prosta korelacji stanowić będzie jednocześnie prostą kalibracji układu pomiarowego dla wybranej wartości R.
Zastępując kondensator dekadowy w układzie pomiarowym (rys.1) kondensatorem o nieznanej pojemności Cx i dokonując pomiaru okresu drgań Tx, wartość iloczynu RCx odczytać można wprost z prostej kalibracyjnej lub pojemność Cx obliczyć można ze wzoru:
![]()
(3)
Przebieg ćwiczenia
Połączyć układ pomiarowy wg. schematu przedstawionego na rys.1.
Po sprawdzeniu układu przez prowadzącego włączyć zasilanie.
Ustawić opornik dekadowy na wartość R= 5 MΩ
Zmieniając wartości pojemności kondensatora dekadowego w zakresie 1÷10 μF (zmiana co 1 μF) zmierzyć czas tn dwudziestu drgań relaksacyjnych dla każdej wartości pojemności C.
Dokonać pomiaru czasu tn dwudziestu drgań relaksacyjnych w sytuacji gdy kondensator dekadowy zostanie zastąpiony przez:
kondensator C1
kondensator C2
kondensatory C1i C2 połączone szeregowo
kondensatory C1i C2 połączone równolegle
Obliczyc wartości iloczynów RC i okresów T drgań badanych w pkt.4 oraz wartości okresów T1, T2, Ts, Tr drgań badanych w pkt.5.
Wyniki pomiarów czasów tn i okresów drgań zapisać w tab.1.
Obliczyc parametry prostej regresji (a - współczynnik kierunkowy, b - wyraz wolny) na podstawie wartości y =T, x =RC.
Wartości parametrów a i b wpisać do tab.1 jako wartości odpowiadającym im wielkościom fizycznym.
Sporządzić wykres T=f(RC) i narysować na nim wyznaczoną prostą kalibracji oraz nanieść punkty odpowiadające wynikom pomiarów z pkt.5.
Obliczyć wartości pojemności badanych kondensatorów C1 i C2 oraz wartośc pojemności szeregowego Cs i równoległego Cr połączenia tych kondensatorów ze wzoru (3).
Obliczyć wartości pojemności zastępczej kondensatorów C1 i C2 połączonych szeregowo (Czs) i połączonych równolegle (Czr).
Obliczyć względne różnice δ= |Cs-Czs|/Czs i δ= |Cr-Czr|/Czr wyrażone w procentach pomiędzy wartościami Cs i Czs oraz Cr i Czr.
Wyniki obliczeń z pkt. 11÷13 zestawić w tab.2.
Tab.1.
C [μF] |
1 |
2 |
... |
10 |
C1 |
C2 |
Cs |
Cr |
RC [s] |
|
|
|
|
|
|
|
|
tn [s] |
|
|
|
|
|
|
|
|
T [s] |
|
|
|
|
|
|
|
|
K= |
To= |
|||||||
Tab.2.
C1 [μF] |
C2 [μF] |
Cs [μF] |
Czs [μF] |
δ [%] |
Cr [μF] |
Czr [μF] |
δ [%] |
|
|
|
|
|
|
|
|
Wymagania
wyładowanie jarzeniowe w gazach rozrzedzonych.
pojemność elektryczna przewodników i kondensatorów.
energia pola elektrycznego kondensatorów.
łączenie kondensatorów i pojemność zastępcza.
ładowanie i rozładowanie kondensatora w układzie RC: charakterystyki graficzne i ilościowy opis tych procesów ( Q(t), U(t), I(t) ).
Wyszukiwarka
Podobne podstrony:
Ćwiczenie nr 65, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65
Antropologia Cwiczenia 01 id 65 Nieznany (2)
Ćwiczenie 65, Studia, 1 rok, od Magdy, FIZYKA, Fizyka, Labolatorium
65 b, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwiczenie nr65b
Antropologia Cwiczenia 05 id 65 Nieznany (2)
Antropologia Cwiczenia 07 id 65 Nieznany (2)
Antropologia Cwiczenia 04 id 65 Nieznany (2)
Do cwiczenia 13 DL1 49 R 65
Ćwiczenie 65
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
więcej podobnych podstron