TEORIA NIEZAWODNOŚĆI I BEZPIECZEŃSTWA

28-02-99

mgr inż. Tomasz Rutkowski - Tel.: [phone]; Nowa Technologia 215c, ul. Narbutta

EGZAMIN + INDEX (III terminy)

LITERATURA:

1. Zbiór zadań; prof. Dobiesław Bobrowski - „Metody matematyczne teorii niezawodności w przykładach i zadaniach” WNT '85;

2. Karpiński, Firkowicz - „Zasady profilaktyki obiektów technicznych” PWN '81;

3. Skrypt; prof. Ważyńska-Fiok - „Podstawy teorii eksploatacji i niezawodności systemów transportowych” PW

4. Gniedenko, Bielajew, Sołowjew - „Metody matematyczne w teorii niezawodności” '68

EKSPLOATOWANIE

UŻYTKOWANIE OBSŁUGIWANIE PRZECHOWYWANIE

urządzenie to wykonuje urządzenie nie pracuje, a my ani my nie pracujemy dla urządzenia

pracę dla nas pracujemy przy urządzeniu ani urządzenia dla nas - przerwy

- czynności o charakterze pro- między używaniem a obsługą

filaktyczno-zapobiegawczymi

- przywrócenie do stanu przy-

datności zepsutego obiektu

- obsługa techniczna

- serwis

MODELE MATEMATYCZNE

M. deterministyczne M. probabilistyczne

(losowe); (na znane wymuszenie odpowiedź

nie jest

jednoznaczna; czyli

może być to lub to)

Zbudowanie modelu probabilistycznego zmusza do określenia:

• zbioru zdarzeń elementarnych;

• rodziny zdarzeń losowych;

• miary probabilistycznej (taka funkcja, która zdarzeniu przyporządkowuje pewną liczbę; liczba ta musi być dodatnia) ta miara musi spełniać następujące warunki:

* P(Ω) = 1 (zdarzenie pewne);

0 ≤ P(A) ≤ 1

* P(Ω) = ø (zdarzenie niemożliwe);

dowolne zdarzenia A

* P (A ∪ B) = P (A) + P (B) - P (A ∩ B)

Jeżeli zdarzenia A i B są niezależne, czyli nie mają części wspólnej, to iloczyn tych zdarzeń jest zbiorem

pustym - zdarzeniem niemożliwym.

PRAWDOPODOBIEŃSTWO WARUNKOWE

P(A / B) =
iloczyn tych zdarzeń

PRAWDOPODOBIEŃSTWO CAŁKOWITE

P(B) =

Żeby opisać procesy eksploatacji potrzebna jest:

Zmienna losowa - pewna wielkość liczbowa, która przyjmuje wartości w zależności od wyniku pewnego doświadczenia.

Co jest potrzebne by powiedzieć, że jest znana?

1. Zbiór wartości, jakie ta zmienna losowa może przyjmować.

2. Prawdopodobieństwo z jakim te wartości są przyjmowane.

Rozkład zmiennej losowej - funkcja, która w sposób jednoznaczny wartościom zmiennej losowej

przyporządkowuje prawdopodobieństwo przyjęcia przez zmienną losową właśnie tej wartości.

Zmienna losowa dyskretna (skokowa, punktowa) - kiedy zbiór jej wartości jest skończony lub co najmniej przeliczalny.

Zmienna losowa ciągła - zbiór wartości może być ograniczony ale jest nieprzeliczalny; pomiędzy dwie dowolne wartości tej zmiennej (dwie liczby rzeczywiste) możemy włożyć nieskończenie wiele innych wartości (liczb rzeczywistych) (np. temperatura).

Dyskretyzacja zmiennej losowej - ze zmiennej losowej ciągłej robimy dyskretną np. przy temperaturze korzystamy z termometru o dokładności (podziałce) 0,01ºC.

Dystrybuanta zmienna losowa

F(x) = P(X < x)

dana wartość

własności:

Dystrybuanta jest funkcją niemalejącą

to

x₁ < x₂ ⇒ F(x₁) ≤ F(x₂)

P(a ≤ X < b) = F(b) - F(a)

dystrybuanta

Gęstość prawdopodobieństwa zmiennej losowej - granica, do której dąży iloraz prawdopodobieństwa tego, że zmienna losowa przyjmie wartość należącą do danego przedziału, do długości tego przedziału, gdy długość ta dąży do zera.

klasyczna definicja pochodnej

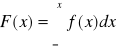
Wartość oczekiwana zmiennej losowej (E) - jedna konkretna liczba

- większa od najmniejszej wartości jaką zmienna losowa może przyjąć;

- mniejsza od największej wartości jaką zmienna losowa może przyjąć.

Np. rzut kostką. Wartości 1, 2, 3, 4, 5, 6.

symbol wartości oczekiwanej zmiennej losowej zmienna losowa

czyli =
⇒ wartość oczekiwana zmiennej losowej

Jeżeli chodzi o wartość oczekiwaną zmiennej losowej ciągłej, to:

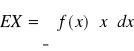
Momenty

E(X - c)ⁿ - moment rzędu n zmiennej losowej względem punktu c.

Z momentem zwykłym mamy do czynienia gdy c = 0

Jeżeli zamiast c występuje liczba = wartości oczekiwanej zmiennej losowej, to mamy do czynienia z momentem centralnym
.

f(x)

EX = E(X - 0)¹

x

gęstość prawdop. zmiennej losowej

II moment centralny

E(X - EX)² = Var X

wariancja zmiennej losowej X

Wariancja zmiennej losowej - miara skupienia zmiennej losowej wokół wartości oczekiwanej.

f(x)

EX x

= σ (sigma - duża) → odchylenie standardowe (im mniejsze wartości przyjmuje σ tym zmienna losowa jest bardziej skupiona).

Niezawodność urządzenia - zdolność urządzenia do spełniania określonych wymagań w określonych warunkach.

OBIEKTY PROSTE JEDNOKROTNEGO DZIAŁANIA

Jednokrotność działania - obiekty nieodnawialne

Obiekty dwustanowe - binarne - jeden z dwóch wzajemnie wykluczających się stanów np. żarówka działa lub nie.

Zmienna losowa

T - czas poprawnej pracy obiektu - jaki upływa od momentu gdy urządzenie rozpoczyna działanie do chwili gdy przechodzi ono w stan niezdatności.

Stan graniczny...?

Poziom zawodności i niezawodności...?