Temat:
Zjawisko Halla w półprzewodnikach
Wydział AE i I . rok I .
semestr II .
grupa V .
sekcja 3 .
Michał Męcik .
Piotr Krawczyk .
1. WPROWADZENIE.
Celem tego ćwiczenia jest zapoznanie się ze zjawiskiem Halla w półprzewodnikach poprzez wyznaczenie zależności napięcia Halla ( UH) od prądu ( IH ) płynącego przez półprzewodnik przy ustalonej wartości pola magnetycznego.
Zjawisko to zostało po raz pierwszy zaobserwowane przez E.H. Halla w 1879 roku i polega na oddziaływaniu pola magnetycznego na poruszające się nośniki ładunku, co jest widoczne w postaci poprzecznej różnicy potencjałów (zwanej napięciem Halla UH). Wartość tego napięcia jest wprost proporcjonalna do natężenia poprzecznego pola elektrycznego przeciwdziałającego sile Lorentza
e*v*B = -e*EH
UH= EH*b
gdzie: e - ładunek elektronu,
v - prędkość elektronów,
B - indukcja magnetyczna,
EH - natężenie poprzecznego pola elektrycznego,
b - szerokość płytki półprzewodnika.
Napięcie Halla można więc wyrazić wzorem: UH = -v*B*b
Zależy ono jak widać od prędkości nośników ładunku, która jest związana z natężeniem prądu płynącego przez półprzewodnik
IH = Q/t = e*n*V/t = e*n*b*d*v
gdzie: n - gęstość objętościowa elektronów w półprzewodniku
d - grubość płytki
Wielkość charakteryzująca zjawisko Halla, czyli tzw. stała Halla RH jest zdefiniowana następująco:
a) RH = -1/(n*e)
dla ujemnych nośników ładunku (elektronów) o koncentracji n
b) RH = 1/(p*e)
dla nośników dodatnich (dziur) o koncentracji p.
W oparciu o podane wcześniej zależności można wyprowadzić wzór na napięcie Halla w postaci :
UH = RH*IH*B/d
Wiedząc, że indukcja w solenoidzie :
B = m*N*IS / l
gdzie: m - przenikalność magnetyczna próżni,
N - liczba zwojów,
IS - prąd płynący w solenoidzie,
l - długość solenoidu.
możemy w łatwy sposób wyznaczyć stałą Halla oraz obliczyć koncentrację nośników ładunku w płytce hallotronu wyznaczając zależność napięcia Halla UH od prądu IH płynącego przez hallotron dla kilku ustalonych wartości prądu IS płynącego przez solenoid.
2. OPIS PRZEBIEGU ĆWICZENIA
Pomiary przeprowadzono w układzie przedstawionym na rysunku.
Solenoid S (o liczbie zwojów N i długości l ) jest źródłem pola magnetycznego. W jego uzwojeniu płynie prąd IS o stałym natężeniu. Pole magnetyczne wewnątrz solenoidu można uważać za jednorodne. Wartość indukcji magnetycznej B wyznaczamy ze wzoru
B = m*N*IS /l
gdzie: m - przenikalność magnetyczna próżni,
N - liczba zwojów solenoidu,
IS - prąd płynący w solenoidzie,
l - długość solenoidu.
Solenoid w ćwiczeniu, miał N=3000 zwojów oraz l=97.5 cm. Autotransformator służy do regulacji prądu IS. Wewnątrz solenoidu umieszczona jest płytka półprzewodnika (hallotron), której grubość wynosi d=2 mm. Opornik R1 służy do kompensacji napięcia asymetrii, które powstaje na skutek niedokładności wykonania hallotronu. Oporniki R2 i R3 służą do regulacji prądu IH. Opornik R2 służy do regulacji zgrubnej, a R3 do regulacji dokładnej.
Ćwiczenie polega na wykonaniu kilku pomiarów dla różnych prądów IH. Przebieg jednego pomiaru można podzielić na następujące etapy:
- ustawienie IS=0 za pomocą autotransformatora,
- ustawienie żądanego prądu IH za pomocą oporników R2 i R3,
- kompensacja napięcia asymetrii za pomocą opornika R1,
- ustawienie kilku wartości prądu IS (za pomocą autotransformatora) i odczytanie odpowiadających im napięć UH (za pomocą miliwoltomierza cyfrowego).
3. OPRACOWANIE WYNIKÓW POMIARÓW
Zależność liniową między UH a IH można przedstawić w postaci
UH = a*IH+b
a,b - współczynniki dla prostej dopasowanej metodą najmniejszych kwadratów.
W rzeczywistości ze względu na różne błędy zależność ta nie jest liniowa.
Zależności przedstawiono na wykresach.
Obliczenia wartości a,b dla różnych wartości prądu IS zostały przeprowadzone na komputerze. Wyniki obliczeń przedstawiono w tabeli.
IS
IH -------------------------------------------------------------------------
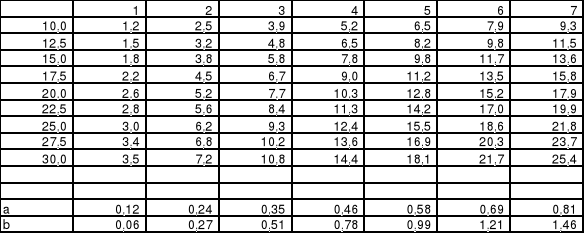
Dla każdej wartości współczynnika a obliczono wartość stałej RH oraz koncentracje nośników ładunku w płytce półprzewodnika.
RH = (a*d*l)/(m*N*IS)
n = -1/(e*RH)
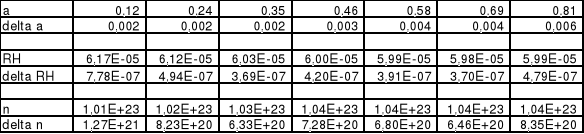
Wartości średnie ważone wynoszą:
a = (0.042 +/- 0.001)
RH = (6.0 +/- 0.2)*10-5 m3/C ,
n = (1.04 +/- 0.01)*1023 m-3 .
4. ANALIZA UZYSKANYCH WYNIKÓW
Na błąd wyznaczenia stałej Halla RH wpływają niesymetryczność samej płytki, błędy pomiarów, wpływ pola magnetycznego na mierniki elektryczne. Sporządzając wykresy charakterystyk UH=f(IH) przy IS=const, zauważamy liniową zależność UH od IH. Pewne punkty wykresów wykazują odstępstwa od tej zależności. Jest to spowodowane niedokładnościami samych pomiarów oraz tym, że hallotron nie jest idealny. RH i n obliczone przy stałych IH i IS różnią się nieznacznie od siebie. Spowodowane jest to m.in. błędami pomiarów, nagrzewaniem się solenoidu, nagrzewaniem się oporników. Głównym powodem tej różnicy były wahania napięcia w sieci, wahania prądu IH co znacznie utrudniało pomiary i było powodem wystąpienia znacznych błędów odczytu mierzonych wielkości.
Liniowa zależność UH=f(IS) mówi nam także o samym napięciu Halla pojawiającym się w płytce półprzewodnika pod wpływem działania pola magnetycznego. Im większe natężenie prądu IS tym większa liczba nośników ładunku zostaje przesunięta i tym większa różnica potencjałów wytwarza się między brzegami płytki. Większe pole magnetyczne dla danego prądu IH powoduje powstanie silniejszego poprzecznego pola elektrycznego, które dąży do zrównoważenia siły FL=q*v*B i napięcie Halla liczone ze wzoru
UH=EH*b
gdzie : EH - natężenie pola elektrycznego ,
b - odległość między ściankami płytki.
także się zwiększy.
Wyszukiwarka
Podobne podstrony:
Prosze przetlumaczyc tekst1, materiały liceum i studia, Łacina
TEKST1
TEKST1
zad tekst1, Matematyka gimnazjum, sprawdziany-Matematyka gimnzjum, klasa1
retoryka, tekst1, Retoryka - wykłady
tekst1 NFEYXJLMTY26KHCNBRK2QLADL7RFNQ4GWBZX2NA
IT tekst1 Zuza BŚ
Kosmos tekst1
Prosze przetlumaczyc tekst1, materiały liceum i studia, Łacina
D tekst1
tekst1 (2) doc
tekst1
Tekst1
tekst1
Community Education Being local tekst1(1)
więcej podobnych podstron