Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię: Czuryłowski Krzysztof
|
Symbol grupy: EDi.2.1 |
|||||
Data wyk. Ćwiczenia: 97.03.12 |
Symbol ćwiczenia: 13.1. |
Temat zadania: Wyznaczanie ciepła topnienia lodu |
||||
|
Zaliczenie:
|
Ocena: |
Data: |
Podpis |
|
|
Tabela pomiarów
|
mk [kg] |
mw [kg] |
m [kg] |
Tp [K] |
Tp [K] |
ck [J/kgK] |
cw [J/kgK] |
ct [J/kg] |
ct [J/kg] |
δmax [%] |
δpop [%] |
||
1 |
0,0787 |
0,1956 |
0,0441 |
293,56 |
283,16 |
896 |
4128 |
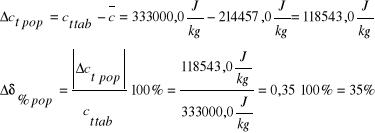
165722,22 |
214457,0 |
5,4 |
35 |
||
2 |
0,0787 |
0,2053 |
0,0680 |
297,36 |
276,76 |
|
|
263191,76 |
|
|
|
||
Opracowanie wyników.

Krótka teoria.
Przemiany fazowe.
Fazą nazywamy zbiór części układu termodynamicznego, jednakowych pod względem własności fizycznych i chemicznych. Każdą fazę charakteryzuje określona budowa cząsteczkowa, której odpowiada określona wartość energii wiązania. Jeśli zwiększy się średnią energię wiązania danej fazy, to ciało zmieni fazę. Zmiany faz są procesami energetycznie odwracalnymi.
Ciała stałe dzielą się na dwa rodzaje o różnych właściwościach fizycznych: krystaliczne i bezpostaciowe.
Rys 1 Krzywe zmian temperatury zachodzących podczas topnienia ciała.
Rys 1 przedstawia krzywą zmian temperatury zachodzących podczas topnienia ciała
krystalicznego i ciała stałego bezpostaciowego.
Punkt A - temperatura topnienia ciała krystalicznego
Odcinek AB - topnienie ciała krystalicznego
Punkt B - przejście całej masy w ciecz
Przegięcie na krzywej b oznacza zakres mięknięcia ciała bezpostaciowego. Przejście ciała stałego w ciecz odbywa się w sposób ciągły.
![]()
Ilość energii Qt jaka należy dostarczyć ciału, aby jego jednostkę masy przeprowadzić w stan ciekły bez zmian temperatury nazywamy ciepłem topnienia
Jednostką miary ciepła topnienia jest dżul na kilogram.
Pod danym ciśnieniem każda ciecz wrze w określonej temperaturze. Gdy ciecz wrze w naczyniu zamkniętym to po pewnym czasie ustala się stan równowagi między cieczą a parą.
Ciała stałe parują na swojej w każdej temperaturze. Nad powierzchnią ciała stałego zamkniętego w naczyniu o stałej objętości wytwarza się para nasycona. Przebieg wszystkich trzech możliwych stanów równowagi międzyfazowej przedstawia wykres na Rys 2.
Rys 2. Wykres fazowy wody
Rozpatrzmy przykładowe przejście ciała ze stanu ciekłego w gazowy.
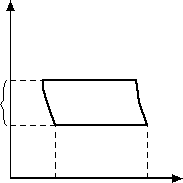
Ciecz w cylindrze pod tłokiem podajemy izotermicznemu rozprężaniu nie zmieniając ciśnienia. Aby rozprężanie przebiegało izobarycznie, mieszanina musi otrzymać z zewnątrz ciepło Qp=mcp Przyrost objętości ΔV= V'0 - V0 , gdzie V'0 jest objętością pary, V0 - objętością cieczy. Praca wykonana podczas tego rozprężania
W1=p(V'0 - V0)
Dokonujemy teraz nieskończenie małego, adiabatycznego zwiększania objętości (krzywa BC) - temperatura spadnie o wartość dT a ciśnienie pary o wartość dp.
Poddajemy teraz mieszaninę izobarycznemu sprężaniu, podczas którego objętość zmieni się o wartość ΔV (odcinek CD). Praca wykonana przez gaz podczas tego procesu wynosi
W2= -(p-dp)( V'0 - V0)
Sprężanie adiabatyczne zamyka cykl.
Rys 3 Cykl przemiany typu Carnota.
Praca całkowita wynosi W=W1+W2 , sprawność tego cyklu
![]()
Podstawiając odpowiednie wyrażenia za W1, W2, Qp, otrzymujemy
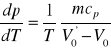
Objętość cieczy V0 jest znikomo mała w stosunku do objętości pary, więc w pewnym przybliżeniu para spełnia równanie gazu doskonałego,
Wzór powyższy nosi nazwę wzoru Clapeyrona - Clausiusa i stosuje się do wszystkich przemian fazowych.
Wyznaczanie ciepła topnienia
Temperatura topnienia lodu w warunkach normalnych wynosi 273.15 K .
W trakcie topnienia lodu temperatura powstającej z niego wody jest równa temperaturze lodu, aż
do momentu całkowitego stopienia .Ciepło potrzebne do stopienia masy m lodu:
Qt=mct
gdzie ct jest ciepłem topnienia lodu.
Ciepło to pobierane jest od innego ciała o wyższej temperaturze, które pozostaje w kontakcie z lodem, w warunkach laboratoryjnych jest to woda znajdująca się w kalorymetrze.
Jeżeli początkowa temperatura wody i kalorymetru jest Tp a końcowa Tk ,wtedy ciepło oddane przez wodę i kalorymetr wynosi:
Q1=mwcw(Tp-Tk)+mkck(Tp-Tk),
gdzie mw oznacza masę wody w kalorymetrze, mk masę kalorymetru , cw ciepło właściwe wody
ck ciepło właściwe kalorymetru
Do pomiarów używa się topniejącego lodu o temperaturze początkowej T0=273.15 K.
Ciepło pobrane przez kalorymetr zostanie zużyte na stopienie lodu i ogrzanie wody powstałej w wyniku stopienia się lodu.
Całkowite ciepło pobrane w tej przemianie
będzie wynosiło :
Q2=mct+mcw(Tk-T0),
gdzie m jest masą lodu i zarazem masą wody z niego powstałej .
Korzystając z zasady bilansu cieplnego możemy napisać ,że Q1=Q2,a więc:
mct+mcw(Tk-T0)=(mwcw+mkck)(Tp-Tk)
po przekształceniu otrzymujemy :
Wykonanie ćwiczenia
Ważymy wewnętrzne naczynie kalorymetru
Napełniamy go do połowy wodą i ważymy ponownie
Z różnicy wyników znajdujemy masę wody
Wstawiamy naczynie do osłony i po pewnym czasie odczytujemy temperaturę wody i kalorymetru
Wkładamy do kalorymetru lód o temperaturze topnienia
Mieszając zawartość kalorymetru odczytujemy najniższą wskazaną temperaturę
Ponownie ważymy naczynie wewnętrzne kalorymetru i znając masę kalorymetru z wodą przed wrzuceniem lodu oraz po jego stopieniu znajdujemy masę lodu.
Dyskusja błędów
Obliczam błąd bezwzględny maksymalny
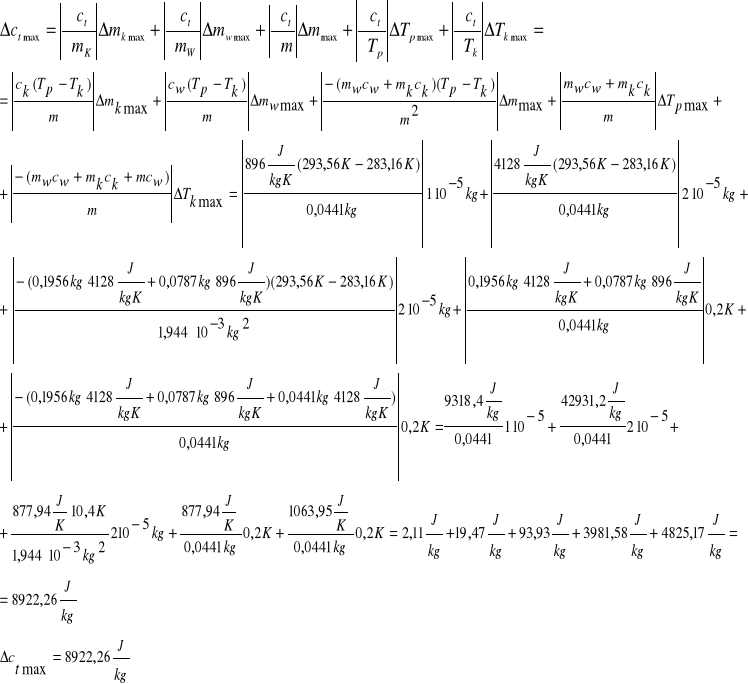
Obliczam błąd względny maksymalny
Obliczam błąd bezwzględny popełniony a następnie błąd względny popełniony
Mając błąd bezwzględny maksymalny można zapisać wynik:
Wnioski i spostrzeżenia
Błąd względny popełniony okazał się znacznie większy od błędu względnego maksymalnego możliwego do popełnienia. Przyczyną tej rozbieżności może być fakt że pomiary wykonane były dla różnych mas lodu co z kolei mogło powodować że długie ustalanie się temperatury naczynia wewnętrznego kalorymetru mogła wpływać na temperaturę wskazywaną przez termometr.
1
3

T
A B
a
b
τ
p
b a
woda
M
para
T
p
A B
D T-dT C
V` V0 V
T
p
dp
![]()
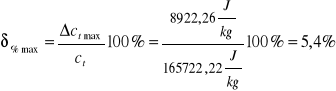
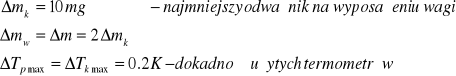
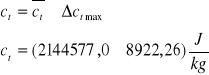
![]()
Wyszukiwarka
Podobne podstrony:
Mech- Wyznaczanie ciepła topnienia lodu(1), Sprawozdania - Fizyka
Wyznaczanie ciepła topnienia lodu, Emilia Wieteska
spraw, 24, Wyznaczanie ciepla topnienia lodu
Mech- Wyznaczanie ciepła topnienia lodu, Sprawozdania - Fizyka
wyznaczanie ciepła topnienia lodu
fizyka, Ciepło topnienia lodu 2 (inne spr.), Temat ćwiczenia nr 32:Wyznaczanie ciepła topnienia lodu
Wyznaczanie ciepła topnienia lodu ćw nr 11, PWSZ Krosno budownictwo, Fizyka
WYZNACZANIE CIEPLA TOPNIENIA LODU, Sprawozdania
C1- Wyznaczanie ciepła topnienia lodu przy pomocy kalorymetru. sprawozdanie, Sprawozdania
Wyznaczanie ciepła topnienia lodu przy pomocy kalorymetru, Studia, Pracownie, I pracownia
Wyznaczanie ciepła topnienia lodu, topnienie lodu
C1 - Wyznaczanie ciepła topnienia lodu metoda kalorymetryczn, Sprawozdania
wyznaczanie ciepła topnienia lodu, Sprawozdania
wyznaczanie ciepla topnienia lodu, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chom
Wyznaczanie ciepła topnienia lodu, Sprawozdania - Fizyka
Wzyanczanie ciepła topnienia lodu przy pomocy kalorymetru, Studia, Pracownie, I pracownia, 27 Wyznac
spr od diany wyznaczanie ciepla topnienia lodu, biologia uj, biologia II, fizyka
więcej podobnych podstron