WOJSKOWA AKADEMIA TECHNICZNA

LABOLATORIUM FIZYCZNE

Grupa szkoleniowa IG-14d Podgr. 3 mgr inż. Paweł Marć

Stańdo Łukasz

.............................. ..............................

(ocena przygot. (ocena końcowa)

do ćwiczenia)

SPRAWOZDANIE

z

PRACY LABOLATORYJNEJ Nr 36

MSZYNA ATWOODA

WSTĘP TEORETYCZNY

Maszyna Atwooda służy do doświadczalnego sprawdzania praw kinematyki i dynamiki. W najprostszym postaci składa się z bloczka K umieszczonego w górnej części pionowego pręta ze skalą S. Przez bloczek przechodzi cienka nić z zawieszonymi na jej końcach ciężarkami o tej samej wadze Mg (M - masa, g - przyspieszenie ziemskie).

Dodatkowe obciążenie k m₀g (k - ilość jednakowych blaszek o masie m₀) jednego z ciężarków wprowadza układ składający się z ciężarka, nici i bloczka w ruch jednostajnie przyspieszony. W maszynie Atwooda zobrazowane są dwa rodzaje ruchów: prostoliniowy jednostajnie zmienny ciężarków orazi obrotowy jednostajnie zmienny bloczka, przez który przełożona jest nić łącząca ciężarki. Opisując ruch ciężarków korzystamy ze wzorów na drogę i prędkość w ruchu jednostajnie zmiennym:

gdzie :

s to droga pokonana przez ciężarek

v₀ to prędkość początkowa ciężarka

t to czas ruchu

a to przyspieszenie ciężarka

Ruch bloczka opisuje równanie:

gdzie:

to kąt obrotu bloczka

to prędkość kątowa bloczka

to prędkość kątowa początkowa

to przyspieszenie kątowe bloczka

W ruchu prostoliniowym ciało charakteryzowane jest przez masę m. Zgodnie z II zasadą dynamiki Newtona siła F nadaje masie m pewne przyspieszenie a :

F = ma =>

Analogicznie równanie do równanie w ruchu obrotowym ma postać:

gdzie:

N to moment siły

J to moment bezwładności

Bryła sztywna obraca się wokół osi l i składa się z k mas punktowych, z których każda ma prędkość liniową v_i zależną od jej odległości obrotu - r_i

oraz energia kinetyczną

gdzie:

to prędkość kątowa jednakowa dla wszystkich m_i.

Energia kinetyczna całej bryły jest równa sumie energii kinetycznych poszczególnych mas punktowych

Porównując powyższy wzór ze wzorem na energię kinetyczną w ruchu postępowym,

widać że odpowiednikiem prędkości liniowej v jest prędkość kątowa
, natomiast masy m całej bryły moment bezwładności

Zależy on od wyboru osi obrotu i rozłożenia masy względem niej (kształtu ciała).

Ruch ciał wchodzących w skład maszyny Atwooda.

Na ciężarek B działają siły ciężkości i naprężenia T₁. Pod wpływem tych sił ciężarek porusza się z przyspieszeniem a, które obliczamy z II zasady dynamiki Newtona:

Podobnie ciężarek A będzie się poruszał pod wpływem sił - ciężkości i naprężenia nici:

Przyspieszenia obydwu ciężarków są jednakowe i wynoszą a. Mają jednak inne zwroty, co uwzględniono w Powyższych równaniach.

Pod wpływem wypadkowego momentu sił T₁ i T₂ bloczek K będzie poruszał się z przyspieszeniem
. Z równania
mamy:

Wyliczając T₁ i T₂ otrzymujemy:

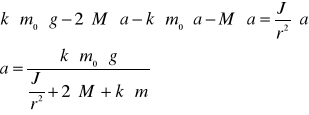
lub

W powyższych wzorach nie uwzględniono sił tarcia.

Poprzez pomiar przyspieszenia a można wyznaczyć moment bezwładności bloczka K:

Przyspieszenie a wyznaczymy mierząc czas t, w którym ciężarki pokonują stałą drogę s .Przy prędkości początkowej równej zeru, wzór
przyjmuje postać
. Wykreślając zależność
powinniśmy otrzymać prostą, której współczynnik kierunkowy jest przyspieszeniem. Umieszczając na bloczku dodatkowe ciało i korzystając z wyprowadzonych zależności można wyznaczyć moment bezwładności J_C, będący sumą momentów bezwładności bloczka Ju i Jb.

Szukana bezwładność jest równa różnicy:

Celem ćwiczenia jest wyznaczenie momentu bezwładności bryły z wykorzystaniem maszyny Atwooda.

OPRACOWANIE WYNIKÓW POMIARÓW

	z pierścieniem		bez pierścienia
	2xgruby	Gruby +cienki	Gruby +cienki	2xgruby
lp	t1 [s]	t2 [s]	t3 [s]	t4 [s]
1	2,140	2,532	1,641	1,415
2	2,431	2,526	1,623	1,409
3	2,151	2,493	1,631	1,419
4	2,158	2,492	1,648	1,421
5	2,152	2,522	1,653	1,422
6	2,141	2,499	1,633	1,409
7	2,165	2,474	1,621	1,406
8	2,152	2,518	1,624	1,423
9	2,159	2,514	1,644	1,417
10	2,141	2,496	1,655	1,415
średnia	2,179	2,507	1,637	1,416
średnia średnich	2,3428		1,52645

Moment bezwładności pierścienia: I = ½·Π·d·ρ·(R₁⁴ - R₂⁴), gdzie:

R₁ to promień zewnętrzny pierścienia

R₂ to promień wewnętrzny pierścienia

d to grubość pierścienia

ρ to gęstość właściwa żelaza

promień bloczka r = 98 ± 1 mm

masa walca 2M = 507 ± 1g

masa cieńszego pierścienia obciążającego m_c = 15,3 ± 0,1 g

masa grubszego pierścienia obciążającego m_g = 31,1 ± 0,1 g

masa pierścienia wynosi 2001 ± 1g

1.Obliczam średnie z czasów z pierścieniem i bez.

t₁=2,179 s

t₂=2,507 s

t₃=1,637 s

t₄=1,416 s

2. Obliczam przyspieszenie układu bez założonego pierścienia.

- dla t₃

a₃ = 2l/t₃² = 2*0,985/1,637² = 0,73 m/s²

-dla t₄

a₄ = 2l/t₄² = 2*0,985/1,416² = 0,98 m/s²

3. Obliczam przyspieszenie układu z założonym pierścieniem.

-dla t₁

a₁ = 2l/t₁² = 2*0,985/2,179² =0,41 m/s²

-dla t₂

a₂ = 2l/t₂² = 2*0,985/2,507² =0,31 m/s²

4. Obliczam moment bezwładności układu bez założonego ciężarka.

I₃ = [(m_c+m_g)g - 2Ma₃ - (m_c+m_g)a₃]r²/a₃ = (0,4552 - 0,3701 - 0,0339)0,009604/0,73 = 6,74*10^-4 kg*m²

I₄ = (2m_gg - 2Ma₄ - 2m_ga₄)r²/a₄ = (0,6102 - 0,4969 - 0,0609)0,009604/0,98 = 1,04*10^-3 kg*m²

5. Obliczam moment bezwładności układu z założonym ciężarkiem.

I₁ = (2m_gg - 2Ma₁ - 2m_ga₁)r²/a₁ = (0,3002 - 0,2079 - 0,0255)0,009604/0,41 = 4,54*10^-3 kg*m²

I₂ = [(m_c+m_g)g - 2Ma₂ - (m_c+m_g)a₂]r²/a₂ = (0,4552 - 0,1572 - 0,0144)0,009604/0,31 = 10,26*10^-4 kg*m²

6. Obliczam moment bezwładności pierścienia.

I_p14 = I₁ - I₄=3,5*10^-3 kg*m²

I_p23 = I₂ - I₃= 3,52*10^-3 kg*m²

7. Rachunek błędów

średni błąd kwadratowy dla czasu t₁ = 0,041 s

średni błąd kwadratowy dla czasu t₂ = 0,056 s

średni błąd kwadratowy dla czasu t₃ = 0,053 s

średni błąd kwadratowy dla czasu t₄ = 0,039 s

średni błąd kwadratowy dla przyspieszenia a₁ = 0,017 m/s-²

średni błąd kwadratowy dla przyspieszenia a₂ = 0,019 m/s-²

średni błąd kwadratowy dla przyspieszenia a₃ = 0,005 m/s-²

średni błąd kwadratowy dla przyspieszenia a₄ = 0,011 m/s-²

średni błąd kwadratowy dla momentu bezwładności I₁ = 6,2*10^-5 kg*m²

średni błąd kwadratowy dla momentu bezwładności I₂ = 0,7*10^-5 kg*m²

średni błąd kwadratowy dla momentu bezwładności I₃ = 7,4*10^-4 kg*m²

średni błąd kwadratowy dla momentu bezwładności I₄ = 6,5*10^-5 kg*m²

średni błąd kwadratowy dla momentu bezwładności I_p14 = 0,9*10^-5 kg*m²

średni błąd kwadratowy dla momentu bezwładności I_p23 = 6,9*10^-5 kg*m²

WNIOSKI I OCENA OTRZYMANYCH REZULTATÓW

W doświadczeniu wyznaczania momentu bezwładności bryły z wykorzystaniem maszyny Atwooda wyznaczona wartość momentu bezwładności pierścienia wyniosła:

I_p14 = I₁ - I₄=3,50*10^-3 ± 0,9*10^-5 kg*m²

I_p23 = I₂ - I₃= 3,52*10^-3± 6,9*10^-5 kg*m²

Otrzymane wyniki nie wiele odbiegają od wartości teoretycznej ,która wynosi 3,69*10^-3 kg*m².Różnica od teoretycznego momentu bezwładności pierścienia spowodowana została błędami pomiarowymi czasu. Mimo fotokomórki i automatycznego włącznika urządzenia, wiele razy mechanizm zacinał się (nie rozpoczynał obliczania czasu lub się nie zatrzymywał). Poza tym wykorzystywany elektromagnes nierównomiernie odczepiał ciężarek. Tarcie bloczka i niedogodności układy również źle wpłynęły na wynik.

Pracę wykonał: ...................................................... dnia 13.06.2004r.

(podpis)

Uwagi prowadzącego ćwiczenia:

2

---