WOJSKOWA AKADEMIA TECHNICZNA

--------------------------------------------------------------------------------------------------------

LABORATORIUM FIZYCZNE

Grupa szkoleniowa C04J mgr inż. Leszek Kubiak
stopień i nazwisko

prowadzącego

GOLONKA Marcin

( imię i nazwisko słuchacza)

ocena końcowa ocena przygot.

do ćwiczenia

SPRAWOZDANIE

Z

PRACY LABORATORYJNEJ Nr 12

Temat: Wyznaczanie współczynnika przewodnictwa cieplnego ciał stałych metodą Christiansena

1. Wstęp teoretyczny.
   

Celem ćwiczenia jest wyznaczenie współczynnika przewodnictwa cieplnego danych ciał stałych metodą Christiansena.

Jak wiadomo, jeśli w różne punkty ciała mają różną temperaturę, to występować tam będzie przepływ ciepła dążący do wyrównania temperatury. Dla różnych ciał przepływ ten odbywać się będzie z różną prędkością, zależącą właśnie od współczynnika przewodnictwa cieplnego. Prawo to opisuje wzór:

gdzie Q - ilość ciepła przechodzącą w jednostce czasu przez jednorodną warstwę o grubości Δx i powierzchni S przy różnicy temperatur ΔT.

λ jest właśnie szukanym współczynnikiem.

Istotą proponowanej metody Christiansena jest uniknięcie konieczności bezpośredniego mierzenia ilości ciepła Q (co jest bardzo kłopotliwe). Metoda ta, jako metoda porównawcza, odnosi badaną wielkość do wzorcowego współczynnika przewodnictwa cieplnego, który jest dany. Ostatecznie zatem do wyznaczenia wielkości λ należy posłużyć się wzorem:

λ_x - szukana wielkość;

λ₀ - wartość współczynnika przewodnictwa cieplnego ciała wzorcowego;

d_x - grubość warstwy ciała badanego;

d₀ - grubość warstwy ciała wzorcowego;

ΔT_x - spadek temperatury na ciele badanym;

ΔT_x - spadek temperatury na ciele wzorcowym;

2. Wyniki pomiarów.
   
   

T[°C]	ok. 30	ok. 40
V1	1,34	1,56
V2	1,17	1,32
V3	1,19	1,35
V4	0,94	1

plexiglas: d₀ = 14 ± 0.5 mm λ₀ = 0.17 kcal / (m*deg*s)

textolit: d_x = 10.7 ± 0.1 mm
= 0.041 mV/K


mV





3. Obliczenia


Ponieważ temperatura jest wprost proporcjonalna do wskazania galwanometru (w mV), a we wzorze mamy do czynienia ze stosunkiem temperatur, to współczynnik
skróci się. Dodatkowo wiadomo, że czułość obu termopar jest jednakowa, zatem wzór przyjmie postać:



Następnie wyliczam względny i bezwzględny błąd wartości
ze wzoru: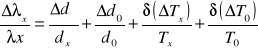


Do obliczeń korzystam z pomocy programu Excel.

temp.	lp	V	T		ΔT	λx	Δλx/λx	Δλx
30	1	1,34	32,683	∆Tx	4,146	0,19107	0,00452	0,00086
		2	1,17						28,537
		3	1,19						29,024	∆To	6,098
		4	0,94						22,927
	40	1	1,56						38,049	∆Tx	5,854	0,18948	0,00452	0,00086
		2	1,32						32,195
		3	1,35						32,927	∆To	8,537
		4	1,00						24,390




4. Wnioski


Po wykonaniu odpowiednich obliczeń ostateczne wartości współczynników przenikalności cieplnej pleksiglasu wynoszą:

λ_x = 799,729±0,012W/(m⋅K) przy temperaturze grzejnika ok. 30⁰ C

λ_x =793,065±0,011 W/(m⋅K) przy temperaturze grzejnika ok. 40⁰ C

W doświadczeniu, aby strumień cieplny przepływający przez płytki był niezachwiany, grubość płytek powinna być nieskończenie mała. Błąd wynika także z tego, że płytki wykonane są z ciała sztywnego. W ten sposób utrudniony jest kontakt cieplny między nimi, czego nie jest w stanie naprawić nawet gumowa podkładka. Słaby kontakt cieplny utrudnia ustalenie się równowagi strumienia cieplnego, a to ma wpływ na bezpośredni pomiar napięć.

Moje wyniki obarczone są błędem około 6%, tak więc są dość dokładne.

---