WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM FIZYCZNE

Grupa szkoleniowa ..EN 13 Krajewski

Ostrowska Urszula

....................................... ..............................................

(ocena przygotowania. (ocena końcowa)

do ćwiczenia)

SPRAWOZDANIE

Z

PRACY LABORZTORYJNEJ Nr. 24

Rezonans w obwodach elektrycznych

.................................. ................................

(ocena przygotowania do ćwiczenia) (ocena końcowa)

Cel ćwiczenia.

Celem ćwiczenia było zbadanie własności obwodu rezonansowego złożonego z elementów rzeczywistych RLC oraz wyznaczenie charakterystyk częstotliwościowych napięć.

1. Opis teoretyczny

Zjawisko rezonansu związane jest z wymuszonymi drganiami układów drgających, np. mechanicznych lub elektrycznych. Pojęcie wymuszenia drgań oznacza, że obwód drgający nie został wytrącony z równowagi, lecz cały czas działa na niego siła.

i(t) L R

Układ rezonansowy RLC

W pewnym momencie na kondensatorze C został zgromadzony ładunek q, a prąd płynący w cewce i oporniku jest równy zeru, następuje rozładowanie kondensatora, zaczyna płynąć prąd określony zależnością:

dq(t) / dt = i

W miarę gdy ładunek q na kondensatorze zmniejsza się, maleje zgromadzona w nim energia elektryczna:

u_E = q² / 2C

Wzrasta natomiast energia pola magnetycznego gromadzona w cewce:

u_B = L i² / 2

W rezultacie pole elektryczne maleje, pole magnetyczne wzrasta, a energia zawarta w polu elektrycznym kondensatora zmienia się na energię pola magnetycznego cewki. W procesie tym przez opornik przepływa prąd wydzielając na nim ciepło Joule'a i następuje zamiana energii na ciepło w ilości:

u_J = R i² / 2

Jeden pełny cykl następuje wtedy, gdy pole elektryczne kondensatora ma ten sam zwrot.

2. Wyznaczanie charakterystyk częstotliwościowych układu RLC.

L_o=30,6*10^-3 H

C_o=3,9*10^-9 F

Uo=2,5V

Tabela pomiarowa:

Lp.	f	U1	U2 dla: C1=82 pF	U3 dla: C1=130 pF	U4 dla: C1=240 pF
		[Hz]	[V]	[V]	[V]	[V]	-	-
1	13 000	1,587	0,116	0,236	0,689	-0,0780	27,115385
2	13 100	1,730	0,152	0,309	0,914	-0,0709
3	13 200	1,904	0,196	0,404	1,281	-0,0638
4	13 300	2,111	0,250	0,540	1,806	-0,0567
5	13 400	2,370	0,343	0,741	2,605	-0,0496
6	13 500	2,693	0,474	1,032	3,594	-0,0426
7	13 600	3,103	0,671	1,495	4,133	-0,0355
8	13 700	3,638	0,994	2,240	3,975	-0,0284
9	13 800	4,340	1,513	3,165	3,654	-0,0213
10	13 900	5,239	2,264	3,725	3,535	-0,0142
11	14 000	6,396	3,050	3,809	3,533	-0,0071
12	14 100	7,083	3,296	3,760	3,818	0,0000
13	14 200	6,885	3,292	3,773	4,091	0,0071
14	14 300	6,015	3,016	3,504	3,987	0,0142
15	14 400	4,974	2,323	2,722	3,216	0,0213
16	14 500	4,070	1,588	1,913	2,328	0,0284
17	14 600	3,597	1,063	1,316	1,676	0,0355
18	14 700	2,687	0,732	0,936	1,236	0,0426
19	14 800	2,500	0,524	0,689	0,935	0,0496
20	14 900	2,188	0,409	0,523	0,730	0,0567
21	15 000	1,891	0,275	0,389	0,554	0,0638

3. Wyznaczenie częstotliwości rezonansowej f_r.

Zmieniając stopniowo częstotliwość sygnału podawanego z generatora, ustalono max. wartość mierzonego napięcia u₁. Częstotliwość, przy której u₁ = u_1max, określana jest mianem częstotliwości rezonansowej i oznaczamy ją symbolem: f_r.

Wartość f_r, określona w ćwiczeniu wynosi:

f_r = 14,1 kHz

4. Obliczona częstotliwości rezonansowej f_r

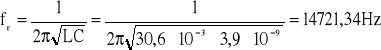
5. Wykreślenie zmierzonej zależności u₁(x), gdzie:

dla pozostałych częstotliwości analogicznie

6. Wyznaczenie dobroci obwodu Q

Przedstawiony powyżej wykres u₁ / u₀ w funkcji „ częstotliwości względnej ” nazywa się krzywą rezonansową. Max. wartość stosunku u₁ / u₀ wyznaczona na wykresie ( dla: f = f_r ) nosi nazwę dobroci układu Q, która w przeprowadzonym ćwiczeniu wyniosła 3,6. Jest to jedno z najważniejszych wielkości charakteryzujących obwód rezonansowy. Dla obwodu szeregowego mówi ona np. ile razy w rezonansie wzrasta napięcie na elementach L i C.

Dla f = f_r dobroć układu:

przy czym nie mamy danego U_o, czyli liczymy Q za pomocą odczytanego B, za pomocą wzoru:

7. Określenie pasma częstotliwości B.

Właściwości filtracyjne obwodu rezonansowego polegają na znacznym wzroście amplitudy napięcia wyjściowego, jeśli częstotliwość napięcia podawanego na obwód leży w paśmie częstotliwości B. Wyznaczenie wartości pasma B, ma więc bardzo duże znaczenie przy rozpatrywaniu obwodów rezonansowych.

Odczytujemy z wykresu B=520

8. Wyznaczenie charakterystyk częstotliwościowych napięć u₂, dla różnych wartości pojemności C.

9. Korzystając z II prawa Kirchoffa, wyznaczam równania drgań wymuszonych w obwodzie RLC przedstawionego na poniższym rysunku.

a). i(t) L R

b).

L R

Układ rezonansowy RLC.

Aby opisać, jak zmienia się prąd w obwodzie RLC skorzystałam z II prawa Kirchoffa, które mówi że suma spadków napięć w obwodzie równa jest zeru.

Z prawa Ohma spadek napięcia na oporniku R jest równy:

u_R(t) = i(t) R

Napięcie na kondensatorze C przyjmuje wartość:

u_c(t) = 1 /C ₀∫^t i(t) d(t) + u_C0

gdzie: u_C0 oznacza wartość napięcia na kondensatorze C w chwili t = 0.

Korzystając z prawa Faraday'a, możemy określić siłę elektromotoryczną, która indukuje się

w cewce L:

u_L(t) = - L d[i(t)] / dt

Mamy więc:

u_L(t) = u_R(t) + u_c(t)

- L di / dt = iR + 1 /C ₀∫^t i(t) d(t)

Korzystając z zależności: u_c(t) = 1 /C ₀∫^t i(t) d(t) + u_C0, oraz ze związku między prądem

a ładunkiem: dq(t) / dt = i, przyjmując, że w chwili początkowej t = 0, q = 0 powyższe równanie przyjmuje postać:

L d²q / dt² + q / C = 0

Wprowadzając oznaczenia:

2β = R / L i ω²₀ = 1 / LC

Otrzymamy ostateczną postać równania:

d²q / dt² + 2β dq / dt + ω²₀ q = 0

WNIOSKI I OCENA OTRZYMANYCH REZULTATÓW

W momencie rezonansu szeregowego wartość napięcia U1 jest maksymalna równa iloczynowi napięcia UE i dobroci obwodu Q. Na podstawie tych wykresów mogę z dużym przybliżeniem określić wartość częstotliwości rezonansowej. Wartość ta dla danych odczytanych z wykresów wynosi 14100 [Hz]. Na podstawie wartości elementów wynosi 14721 [Hz].
Ewentualne rozbieżności wynikają stąd iż wzory te są prawdziwe jedynie dla idealnych elementów R,L,C a tu mają 5% tolerancję, przy uwzględnieni jej częstotliwość zmienia się w zakresie od 14020 do 15496 Hz.

W pojedynczych obwodach kształt krzywej rezonansowej jest dzwonowaty o łagodnych zboczach . W obwodach sprzężonych wartość napięcia U2 jest mniejsza co widać na wykresie i zależna od stopnia sprzężenia któr reguluje CX. Mamy trzy rodzaje sprzężeń.

Dla Cx=82pF amplituda jest mniejsza niż dla obwodu pojedynczego , występuje tu sprzężenie podkrytyczne. Dla drugiej wartości pojemnościi charakterystyka przy wierzchołku jest bardziej płaska i ma bardziej strome zbocza. Dla Cx=240pF wykres posiada trzy punkty ekstremalne takie sprzężenie nazywamy nadkrytycznym. W tym przypadku zwiększa się jeszcze nachylenie charakterystyki na krawędziach pasma natomiast tracimy na amplitudzie , która zmniejsza się do połowy w porównaniu z obwodem pojedynczym.

Trudno jest także na podstawie takich pomiarów jakich dokonaliśmy na pracowni określić te wartości z dużą dokładnością, a ponadto podczas przeprowadzania pomiarów wyraźnie był widoczny wpływ przyrządów pomiarowych na badany układ Dlatego mogliśmy jedynie określić wartości przybliżone. Pomimo tego różnice pomiędzy wartościami obliczonymi a zmierzonymi są niewielkie.

6

4

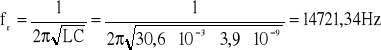
e

C

C

C

---