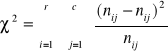
gdzie: ![]()
Korelacja cech jakościowych
Wzór na statystykę χ2 w przypadku, gdy liczba wierszy lub kolumn jest większa niż 2:
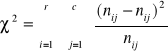
gdzie: ![]()
(dwie sumy oznaczają sumy wierszy i kolumn) [i] oznacza numer wiersza (np. i=1 oznacza 1-szy wiersz) [j] oznacza numer kolumny (np. j=1 oznacza 1-szą kolumnę) [r] oznacza liczbę wierszy [c] oznacza liczbę kolumn
|
sumy w liczniku oznaczają sumę i-tego wiersza (np. 1-szego) oraz sumę j-tej kolumny (np. 2-giej)
[n] oznacza liczbę wszystkich badanych jednostek |
Zadanie 1) W dziale ubezpieczeń samochodowych PZU przypuszcza się, że wysokość odszkodowań samochodowych zależy od typu auta. W tym celu zbadano 1 000 samochodów:
Typ |
Wysokość odszkodowań (w zł) |
Suma |
||
samochodu |
Poniżej 500 |
500 - 1000 |
Powyżej 1000 |
|
Osobowy |
300 |
200 |
100 |
600 |
Dostawczy |
30 |
170 |
200 |
400 |
Suma |
330 |
370 |
300 |
n=1000 |
Czy przypuszczenie to jest prawdziwe? Oceń siłę tej zależności.
ROZWIĄZANIE:
Zaprezentowana tabela nazywa sie tabelą kontyngencji
Składa się z r=2 wierszy oraz c=3 kolumn, więc trzeba zastosować powyższy wzór na χ2, a nie ten uproszczony dla tabel 2x2 (z symbolami a,b,c,d - zadanie 2)
Zaczynamy od zsumowania wszystkich wierszy i kolumn (na czerwono)
Następnie sporządzamy tabelkę pomocniczą:
(i,j) (wypisujemy wszystkie przypadki)* |
|
|
|
1,1 1,2 1,3 2,1 2,2 2,3 |
300 200 100 30 170 200 |
222 180 132 148 120 |
2,2 35,6 78,8 3,3 53,3 |
|
|
|
∑ = 225,7 = χ2 |
* np. 1,3 oznacza 1-szy wiersz oraz 3-cią kolumnę
Suma ostatniej kolumny to statystyka χ2
Następnie obliczamy współczynnik kontyngencji C Pearsona, Cmax oraz Ckor, który da odpowiedź jak jest siła zależności:
od 0 do 0,3 - mała siła zależności
od 0,3 do 0,5 - umiarkowana
od 0,5 do 1 - duża
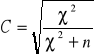
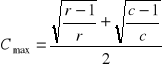
![]()
C = 0,43 Cmax = 0,76 Ckor = 0,57
Odp. Między typem samochodu a wysokością odszkodowania występuje silna zależność (ponieważ Ckor przekroczył 0,5)
Zadanie 2) Zbadano związek między płcią o preferowanym miejscem wyjazdu na wakacje:
Płeć |
Miejsce wyjazdu |
|
|
Morze |
Góry |
Kobieta |
90 |
10 |
Mężczyzna |
20 |
80 |
Oceń jaka jest jego siła.
ROZWIĄZANIE:
Tym razem tabela składa się z 2 wierszy i 2 kolumn, zatem możemy zastosować wzór uproszczony na statystykę χ2:
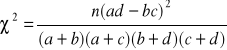
gdzie:
a = 90 |
b = 10 |
c = 20 |
d = 80 |
Dodatkowo n = 200 (tyle było wszystkich badanych osób)
Po obliczeniach otrzymujemy χ2 = 99; C = 0,58; Cmax = 0,71; Ckor = 0,82
Odp. Między płcią a preferowanym miejscem wyjazdu na wakacje występuje silna zależność (ponieważ Ckor przekroczył 0,5)