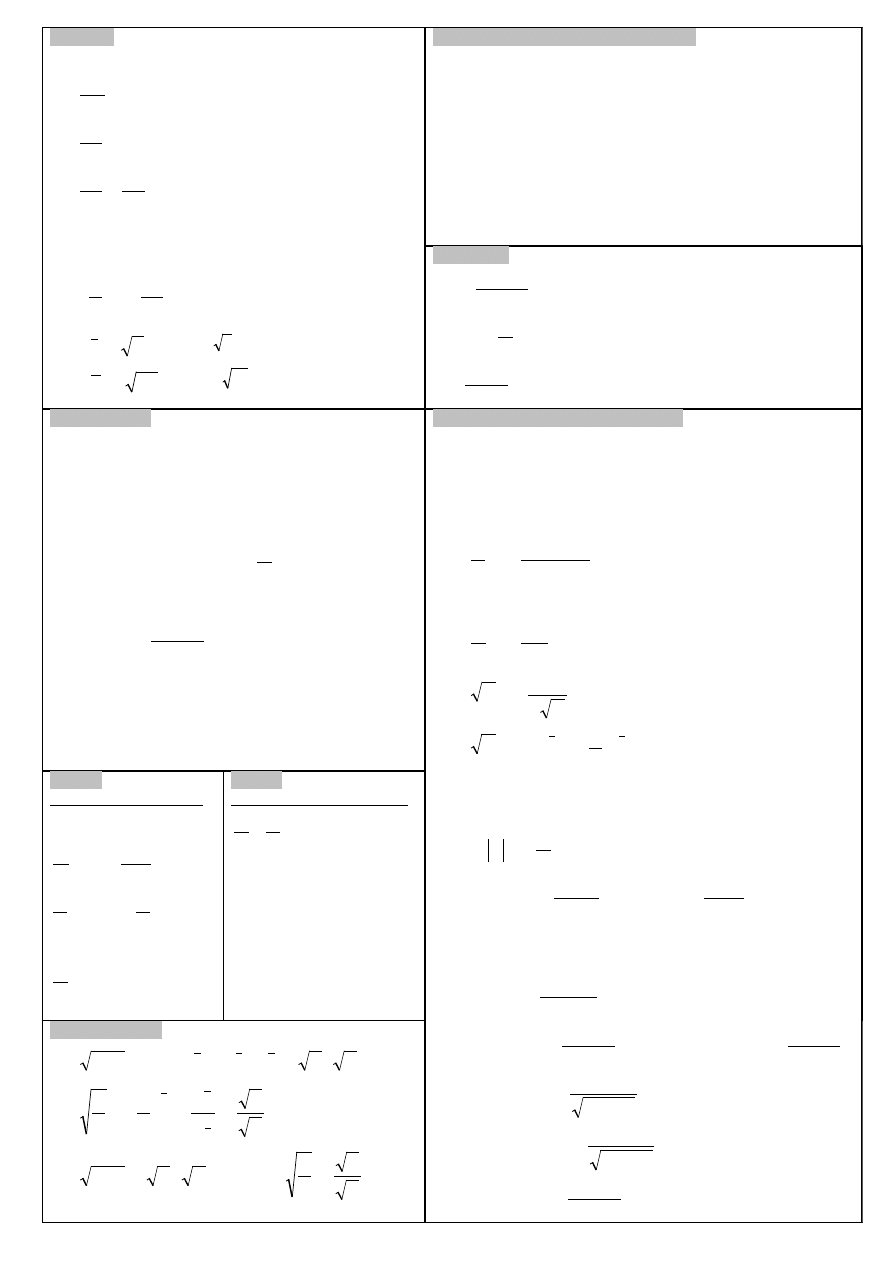
POTĘGI:

1.

m

n

m

n

a

a

a

++++

====

⋅⋅⋅⋅

np: (a

2

·a

3

=a

5

)

2.

m

n

m

n

a

a

a

−−−−

====

np: a

5

/a

3

=a

2

3.

1

a

a

a

0

n

n

=>

=>

=>

=>

====

4.

n

0

n

0

n

a

a

a

a

1

−−−−

====

====

np: 1/a

3

=a

-3

5.

m

n

m

n

a

)

a

(

⋅⋅⋅⋅

====

np: (a

2

)

3

=a

6

6.

n

n

n

b

a

)

b

a

(

⋅⋅⋅⋅

====

⋅⋅⋅⋅

np: (a·b)

2

=a

2

·b

2

7.

n

n

n

b

a

b

a

====













np: (a/b)

2

=a

2

/b

2

8.

n

n

1

a

a

====

np: a

1/3

=

3

a

9.

m

n

m

n

a

a

====

np:a

2/3

=

3

2

a

WZORY SKRÓCONEGO MNOŻENIA:

1.

2

2

2

b

ab

2

a

)

b

a

(

++++

++++

====

++++

2.

2

2

2

b

ab

2

a

)

b

a

(

++++

−−−−

====

−−−−

3.

3

2

2

3

3

b

ab

3

b

a

3

a

)

b

a

(

++++

++++

++++

====

++++

4.

3

2

2

3

3

b

ab

3

b

a

3

a

)

b

a

(

−−−−

++++

−−−−

====

−−−−

5.

)

b

a

)(

b

a

(

b

a

2

2

−−−−

++++

====

−−−−

6.

)

b

ab

a

)(

b

a

(

b

a

2

2

3

3

++++

++++

−−−−

====

−−−−

7.

)

b

ab

a

)(

b

a

(

b

a

2

2

3

3

++++

−−−−

++++

====

++++

GRANICE:

n

2

a

a

S

n

1

n

⋅⋅⋅⋅

⋅⋅⋅⋅

====

e

)

x

1

1

(

lim

x

x

====

++++

∞

∞

∞

∞

→

→

→

→

1

x

x

sin

lim

o

x

====

→

→

→

→

LOGARYTMY:

1.

b

a

c

b

log

c

a

====

<=>

<=>

<=>

<=>

====

dla a>0, a

≠

1, b>0

2.

1

a

log

a

====

bo a

1

=a

3.

0

1

log

a

====

bo a

0

=1

4.

)

y

x

(

log

y

log

x

log

a

a

a

⋅⋅⋅⋅

====

++++

5.

y

x

log

y

log

x

log

a

a

a

====

−−−−

6.

x

log

p

x

log

a

p

a

⋅⋅⋅⋅

====

7.

a

log

x

log

x

log

b

b

a

====

8.

A

a

A

a

log

====

np: 3

log

3

5

=5

9.

A

a

log

A

a

====

np: log

3

3

4

=4

10.

)

x

(

f

ln

)

x

(

f

log

e

====

POCHODNE (RÓŻNICZKOWANIE)

1.

1

)'

x

(

====

2.

0

)'

a

(

====

3.

1

n

n

x

n

)'

x

(

−−−−

⋅⋅⋅⋅

====

4.

)

x

(

'

f

c

))'

x

(

f

c

(

⋅⋅⋅⋅

====

⋅⋅⋅⋅

5.

2

'

g

'

fg

g

'

f

g

f

−−−−

====













6.

'

fg

g

'

f

)'

g

f

(

++++

====

⋅⋅⋅⋅

7.

2

'

x

1

x

1

−−−−

====













8.

x

2

1

)'

x

(

====

9.

1

n

1

3

1

3

x

n

1

)'

x

(

)'

x

(

−−−−

====

====

CIĄGI:
SYMBOLE OZNACZONE

∞

∞

∞

∞

====

∞

∞

∞

∞

++++

∞

∞

∞

∞

∞

∞

∞

∞

====

∞

∞

∞

∞

⋅⋅⋅⋅

∞

∞

∞

∞

0

a

====

∞

∞

∞

∞

,

0

a

====

∞

∞

∞

∞

−−−−

±∞

±∞

±∞

±∞

====

0

a

,

0

a

0

====

∞

∞

∞

∞

====

∞

∞

∞

∞

∞

∞

∞

∞

0

x

a

====

CIĄGI:
SYMBOLE NIEOZNACZONE

∞

∞

∞

∞

∞

∞

∞

∞

;

0

0

;

∞

∞

∞

∞

−−−−

∞

∞

∞

∞

;

∞

∞

∞

∞

⋅⋅⋅⋅

0

;

0

0

;

0

∞

∞

∞

∞

;

∞

∞

∞

∞

0

;

∞

∞

∞

∞

1

10.

a

ln

a

)'

a

(

x

x

====

np: (5

x

)’=5

x

ln5

11.

x

x

e

)'

e

(

====

12.

x

1

)'

x

(ln

====

13.

a

ln

x

1

)'

x

(log

a

====

np: (log

3

x)’ =

ln3

x

1

14.

x

cos

)'

x

(sin

====

15.

x

sin

)'

x

(cos

−−−−

====

16.

x

cos

1

)'

x

tg

(

2

====

PIERWIASTKI:

1.

n

n

n

1

n

1

n

1

n

b

a

b

a

)

b

a

(

b

a

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

⋅⋅⋅⋅

2.

n

n

n

1

n

1

n

1

n

b

a

b

a

b

a

b

a

====

====













====

3.

n

n

n

b

a

b

a

⋅⋅⋅⋅

====

⋅⋅⋅⋅

4.

n

n

n

b

a

b

a

====

17.

x

sin

1

)'

x

ctg

(

2

−−−−

====

21.

2

x

1

1

)'

x

arcctg

(

++++

−−−−

====

18.

2

x

1

1

)'

x

(arcsin

−−−−

====

19.

2

x

1

1

)'

x

(arccos

−−−−

−−−−

====

20.

2

x

1

1

)'

x

arctg

(

++++

====

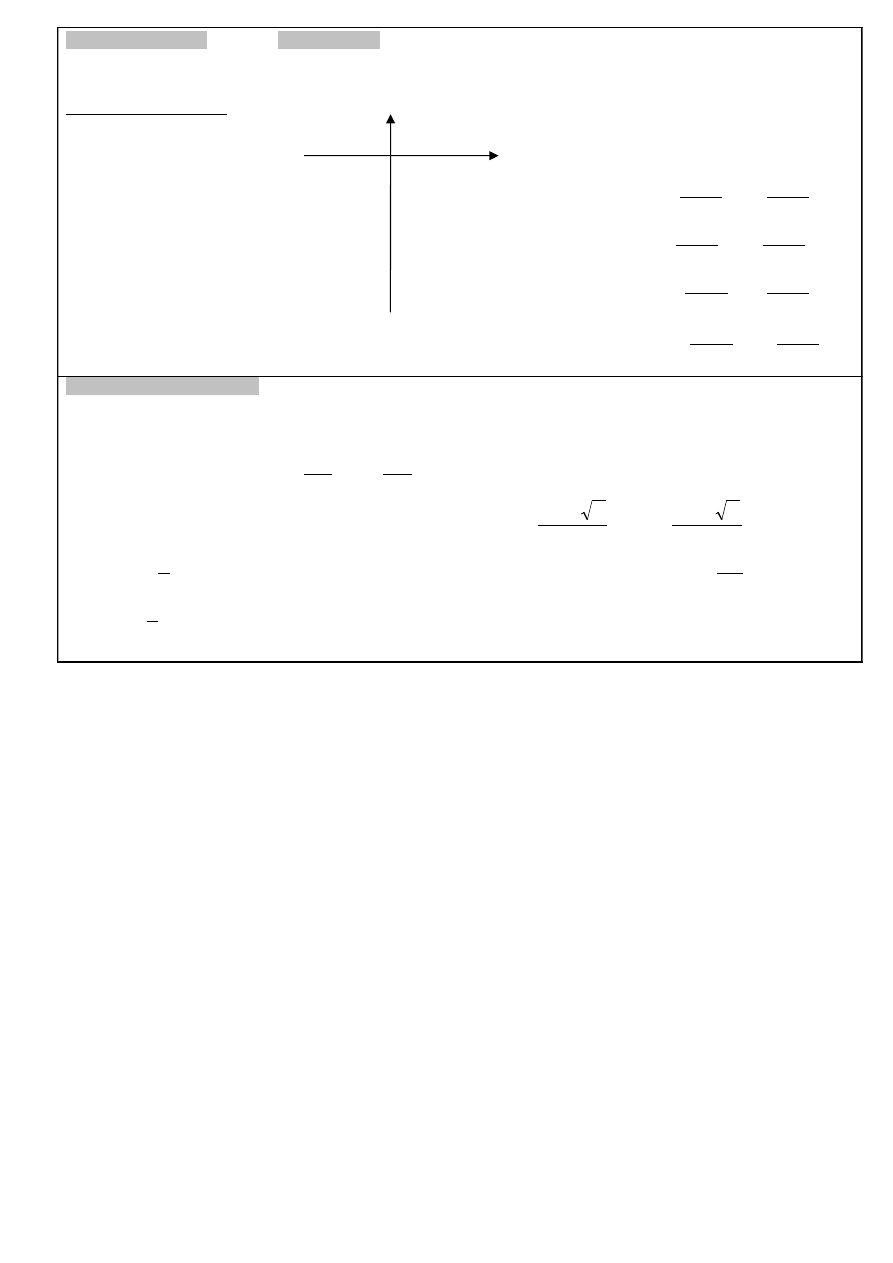
TRYGONOMETRIA:

Π

=180

°

1

x

cos

x

sin

2

2

====

++++

WZORY REDUKCYJNE

1.

αααα

⋅⋅⋅⋅

αααα

====

αααα

cos

sin

2

2

sin

αααα

====

αααα

++++

cos

)

90

sin(

o

2.

αααα

−−−−

αααα

====

αααα

2

2

sin

cos

2

cos

αααα

−−−−

====

αααα

++++

cos

)

270

sin(

o

3.

)

sin(

sin

cos

cos

sin

ββββ

−−−−

αααα

====

ββββ

αααα

−−−−

ββββ

αααα

αααα

====

αααα

−−−−

sin

)

180

sin(

o

4.

2

cos

2

sin

2

sin

sin

ββββ

++++

αααα

⋅⋅⋅⋅

ββββ

−−−−

αααα

====

ββββ

−−−−

αααα

αααα

−−−−

====

αααα

−−−−

sin

)

360

sin(

0

5.

2

cos

2

sin

2

sin

sin

ββββ

−−−−

αααα

⋅⋅⋅⋅

ββββ

++++

αααα

====

ββββ

++++

αααα

6.

2

sin

2

sin

2

cos

cos

αααα

−−−−

ββββ

⋅⋅⋅⋅

ββββ

++++

αααα

====

ββββ

−−−−

αααα

a

nieparzyst

funkcja

)

sin(

sin

parzysta

funkcja

)

cos(

cos

αααα

−−−−

====

αααα

−−−−

αααα

−−−−

====

αααα

7.

2

cos

2

cos

2

cos

cos

ββββ

−−−−

αααα

⋅⋅⋅⋅

ββββ

++++

αααα

====

ββββ

++++

αααα

FUNKCJA KWACRATOWA:

1.

Postać ogólna:

2

2

c

bx

x

y

++++

++++

====

ac

4

b

2

−−−−

====

∆∆∆∆

∆

>0 – 2 miejca zerowe

2.

Postać kanoniczna:

q

)

p

x

(

y

2

++++

−−−−

====

∆

=0 – 1 miejca zerowe

3.

Współrzędne wierzchołka:

a

2

b

p

−−−−

====

;

a

4

q

∆∆∆∆

−−−−

====

∆

<0 – brak miejc zerowych

Wzory Vieta:

a

2

b

x

;

a

2

b

x

2

1

∆

+

−

=

∆

−

−

=

a

b

x

x

2

1

−

=

+

gdy

∆

=0 miejsce zerowe

a

2

b

x

0

−

=

a

c

x

x

2

1

=

⋅

F(a)=F(-a) – funkcja parzysta

,

F(-a)=-F(a) – funkcja nieparzysta

x

1

i x

2

– miejsca

zerowe funkcji

dla

0

≥

∆

II

sin

i

x +

I

sin

i

x +

cos

i

x +

tg

i

x +

ctg

i

x +

III

tg

i

x +

ctg

i

x +

IV

cos

i

x +