1

Matematyka finansowa

Ćwiczenie 7

(rachunek rent)

5. (6.17) Półroczna opłata za 7-semestralne studia zaoczne wynosi 2100 zł z góry. Ile trzeba mieć na koncie w chwili
rozpoczęcia studiów, aby starczyło na czesne za całe studia. Zakładamy stałą nominalną stopę procentową równą 8%
i kapitalizację półroczną.
Odp.: 13 108,49 zł.

Rozwiązanie

I sposób

Oznaczmy przez

j

x

stan konta na początku semestru

j

(

7

,...,

1

=

j

), a przez

0

x

- początkowy stan konta.

Zauważamy, że półroczne oprocentowanie zgromadzonych na koncie środków jest równe 4%, a po zakończeniu
opłat za studia stan konta ma być równy zeru, co zapisujemy następująco:

0

7

=

x

.

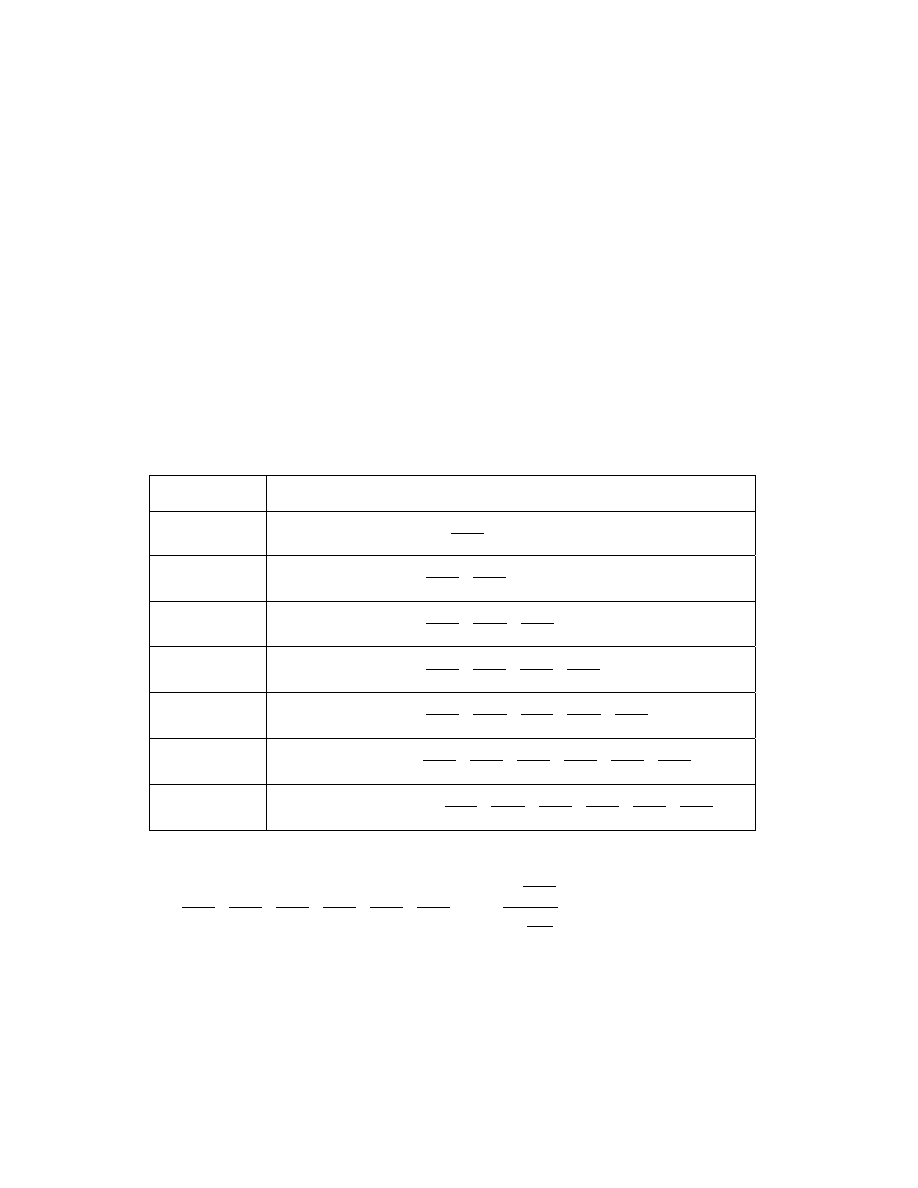
Operacje przeprowadzane na koncie przedstawia poniższa tabela.

Początek

semestru

Stan konta

VII

0

2100

04

,

1

6

7

=

−

=

x

x

;

04

,

1

2100

6

=

x

VI

2100

04

,

1

5

6

−

=

x

x

;

2

5

04

,

1

2100

04

,

1

2100 +

=

x

V

2100

04

,

1

4

5

−

=

x

x

;

3

2

4

04

,

1

2100

04

,

1

2100

04

,

1

2100

+

+

=

x

IV

2100

04

,

1

3

4

−

=

x

x

;

4

3

2

3

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

+

+

+

=

x

III

2100

04

,

1

2

3

−

=

x

x

;

5

4

3

2

2

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

+

+

+

+

=

x

II

2100

04

,

1

1

2

−

=

x

x

;

6

5

4

3

2

1

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

+

+

+

+

+

=

x

I

2100

0

1

−

= x

x

;

6

5

4

3

2

0

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

2100

+

+

+

+

+

+

=

x

Korzystając ze wzoru na sumę ciągu geometrycznego otrzymujemy:

49

,

108

13

24214

,

6

2100

04

,

1

1

1

04

,

1

1

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

04

,

1

2100

2100

7

6

5

4

3

2

0

=

⋅

=

−

−

⋅

=

+

+

+

+

+

+

=

x

.

II sposób

Zauważamy, że opłaty za studia można potraktować jako wypłaty renty, przy czym pierwsza renta jest wypłacana z
góry. Zadanie sprowadza się do wyznaczenia wartości funduszu rentowego.

Dokonajmy poniższych przekształceń:

J.Marcinkowski Rachunek rent

2

(

)

(

)

(

)

(

)

6

7

7

7

7

7

7

0

04

,

0

1

04

,

0

1

04

,

0

1

2100

04

,

0

1

04

,

0

04

,

0

1

1

04

,

0

1

2100

04

,

1

1

04

,

1

04

,

1

1

04

,

1

2100

04

,

1

1

1

04

,

1

1

1

2100

+

⋅

−

+

⋅

=

+

+

−

+

⋅

=

−

−

⋅

=

−

−

⋅

=

x

.

Wyrażenie

(

)

(

)

6

7

04

,

0

1

04

,

0

1

04

,

0

1

+

⋅

−

+

określa wartość czynnika dyskontującego płatnej z góry renty czasowej (dodatek B,

wzór (B.4)): wystarczy w tym celu zauważyć, że

7

,

04

,

0

=

=

n

r

.

Gdyby opłaty za studia wnoszone były z dołu, tj. po upływie semestru, to stan początkowy konta musiałby wynosić

(

)

(

)

31

,

604

12

04

,

0

1

04

,

0

1

04

,

0

1

2100

7

7

0

=

+

⋅

−

+

⋅

=

x

.

Jak podpowiada intuicja, wartość początkowa renty jest w tym przypadku mniejsza: opłaty musimy wnosić w
późniejszych momentach.

6. (6.20) Pan Kowalski chciał kupić samochód, który był wystawiony na giełdzie za 50 000 zł. Zdawał sobie sprawę,
że na koncie osobistym oprocentowanym 16% z kapitalizacją miesięczną ma tylko 45 000 zł. Po dłuższych
negocjacjach sprzedający zgodził się sprzedać Kowalskiemu samochód na raty. Uzgodnili 36 rat miesięcznych po
1500 zł każda i 2000 zł w chwili transakcji. Czy Kowalskiemu wystarczy pieniędzy na ten samochód?

Odp.: Tak.

Rozwiązanie

I sposób

Stan konta: 45 000 PLN.
Stan konta po zawarciu transakcji: 45 000 - 2000 = 43 000 PLN.

Plan spłat i korespondujący z nimi stan konta przedstawia tabela.

Koniec miesiąca

Stan konta

I

1500

12

16

,

0

1

43000

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

II

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

12

16

,

0

1

1

1500

12

16

,

0

1

43000

1500

12

16

,

0

1

1500

12

16

,

0

1

43000

2

............................ ......................................................................................................................................................

36

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛ +

+

+

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

35

36

12

16

,

0

1

...

12

16

,

0

1

1

1000

12

16

,

0

1

43000

Sprawdzamy stan konta po dokonaniu ostatniej, 36 spłaty:

=

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛ +

+

+

⎟

⎠

⎞

⎜

⎝

⎛ +

+

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

12

16

,

0

1

1

12

16

,

0

1

1

1500

12

16

,

0

1

43000

12

16

,

0

1

...

.

12

16

,

0

1

1

1500

12

16

,

0

1

43000

36

36

35

36

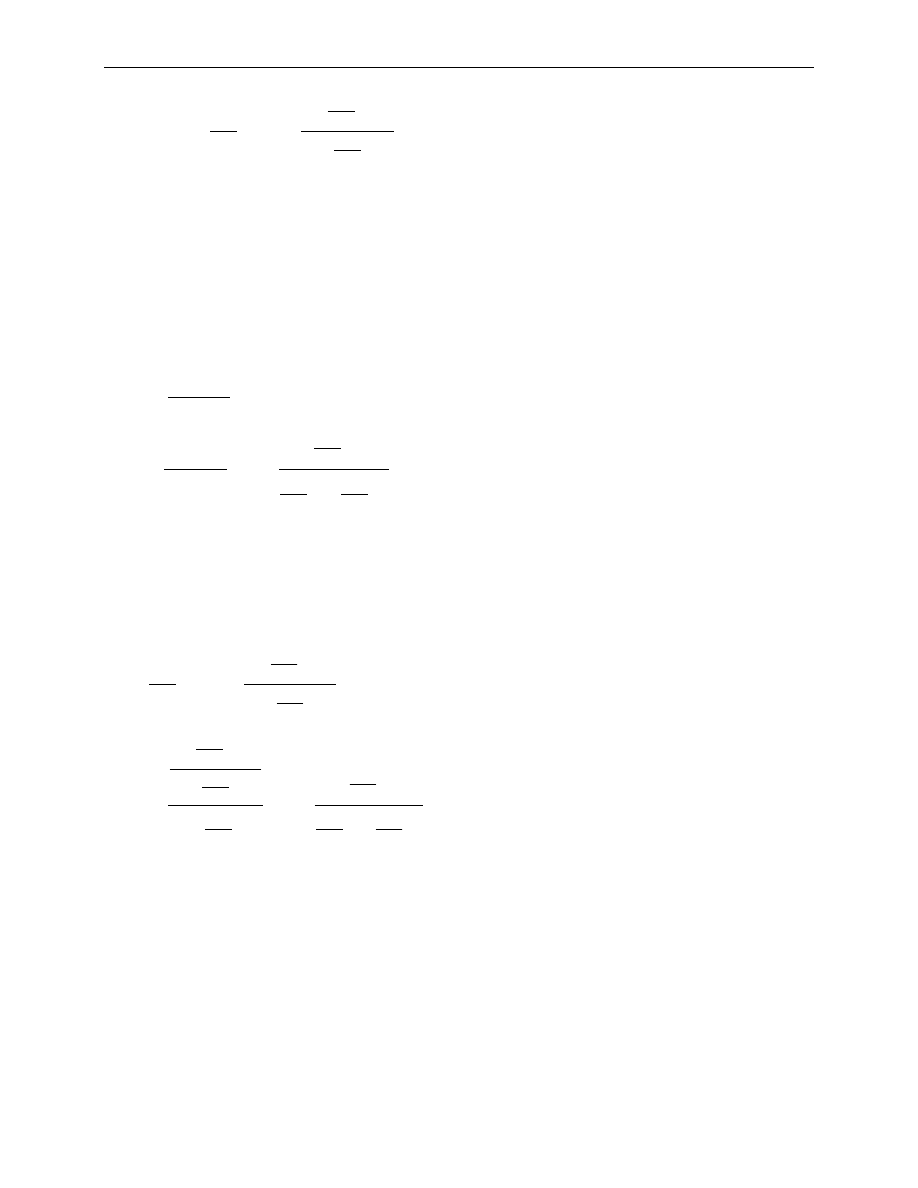
J.Marcinkowski Rachunek rent

3

.

0

24

,

829

67

13

,

271

69

12

16

,

0

1

12

16

,

0

1

1500

12

16

,

0

1

43000

36

36

>

−

=

−

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

Z tego, że stan konta po dokonaniu ostatniej spłaty jest dodatni wynika, że zgromadzona na koncie kwota wystarcza
do sfinansowania transakcji.

II sposób

Zauważamy, że spłaty możemy traktować jako wypłaty zwykłej renty czasowej. Wyznaczmy fundusz rentowy
niezbędny do wypłaty tej renty (36 wypłat po 1500 zł, płatne co miesiąc, poczynając od końca pierwszego miesiąca).
Jeżeli wysokość funduszu rentowego nie jest większa od 43 000 zł (uwzględniamy 2000 zł płatne w momencie
zawarcia transakcji), to zgromadzone na koncie środki wystarczą do sfinansowania transakcji.

W celu wyznaczenia wysokości funduszu rentowego wykorzystujemy czynnik dyskontowania zwykłej renty

czasowej

(

)

(

)

n

n

r

r

r

+

⋅

−

+

1

1

1

dany wzorem 6.3.3. Fundusz ten jest równy:

(

)

(

)

72

,

665

42

12

16

,

0

1

12

16

,

0

1

12

16

,

0

1

1500

1

1

1

1

1500

36

36

=

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

+

⋅

−

+

⋅

n

n

r

r

r

z czego wynika, że zgromadzone na koncie środki (43 000 PLN) wystarczą do przeprowadzenia transakcji.

Komentarz

Dokonajmy przekształceń wzoru otrzymanego przy rozwiązywaniu zadania pierwszym sposobem. Przyjmijmy, że
fundusz rentowy nie jest znany. Mamy

.

12

16

,

0

1

12

16

,

0

1

12

16

,

0

1

1500

12

16

,

0

1

12

16

,

0

1

12

16

,

0

1

1500

,

0

12

16

,

0

1

12

16

,

0

1

1500

12

16

,

0

1

36

36

36

36

36

36

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

>

>

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

−

⎟

⎠

⎞

⎜

⎝

⎛ +

⋅

x

x

Otrzymujemy wzór zastosowany przy rozwiązywania zadania drugim sposobem.

7. (6.19) Na konto bankowe oprocentowane 12% w skali roku z miesięczną kapitalizacją odsetek wpłacono 50 000
zł. Począwszy od końca pierwszego miesiąca rozpoczęto wypłacać z konta co miesiąc stałą kwotę 1000 zł. W którym
miesiącu pojawi się debetowe saldo na rachunku?

Odp.: W siedemdziesiątym miesiącu.

Rozwiązanie

Oznaczmy przez

p

oprocentowanie konta w stosunku miesięcznym. Przeanalizujmy zmiany stanu konta w

kolejnych miesiącach.

J.Marcinkowski Rachunek rent

4

Koniec miesiąca

Stan konta

I

(

)

1000

1

50000

−

+

⋅

p

II

(

)

[

]

(

)

(

)

(

)

[

]

p

p

p

p

+

+

⋅

−

+

⋅

=

−

+

⋅

−

+

⋅

1

1

1000

1

50000

1000

1

1000

1

50000

2

............................ ......................................................................................................................................................

n

(

)

(

)

(

)

[

]

1

1

...

.

1

1

1000

1

50000

−

+

+

+

+

+

⋅

−

+

⋅

n

n

p

p

p

Rozwiązanie zadania sprowadza się do pytania, dla jakich

p

spełniona jest nierówność:

(

)

(

)

(

)

[

]

0

1

...

.

1

1

1000

1

50000

1

>

+

+

+

+

+

⋅

−

+

−

n

n

p

p

p

.

Stosując wzór na sumę ciągu geometrycznego dostajemy:

(

)

(

)

(

)

0

1

1

1

1

1000

1

50000

>

+

−

+

−

⋅

−

+

⋅

p

p

p

n

n

,

(

)

(

)

p

p

p

n

n

1

1

1000

1

50000

−

+

>

+

⋅

.

Podstawiając

01

,

0

=

p

, otrzymujemy:

01

,

1

1

01

,

1

1000

01

,

1

50000

−

>

⋅

n

n

.

Zauważamy, że dla zwiększających się wartości n stan konta zmniejsza się. Rozwiązujemy równanie

01

,

1

1

01

,

1

1000

01

,

1

50000

−

=

⋅

n

n

,

2

01

,

1

=

n

,

2

ln

01

,

1

ln

=

n

,

67

,

69

01

,

1

ln

2

ln

≈

=

n

.

Oznacza to, że maksymalną całkowitą wartością n , dla której stan konta jest dodatni jest 69. Zatem debetowe saldo
pojawi się w 70. miesiącu.

8. (6.6) Dane są dwie renty wieczyste A i B, gdzie:
- renta A w wysokości 1 jest płatna na końcu każdego roku,
- renta B w wysokości 1 jest płatna na końcu co drugiego roku.
Przy danej stopie nominalnej różnica pomiędzy wartością bieżącą renty A a wartością bieżącą renty B wynosi 2 .
Oblicz nominalną stopę procentową.

Odp.: 41,42%.

Rozwiązanie

Oznaczmy przez

( )

A

NPV

i

( )

B

NPV

wartości funduszu rentowego renty A i B. Są one sumami nieskończonych

ciągów wartości bieżących:

( )

(

)

(

)

r

r

r

r

r

r

r

r

A

NPV

1

1

1

1

1

1

1

1

1

1

1

1

1

....

1

1

1

1

2

=

+

+

−

⋅

+

=

+

−

⋅

+

=

+

+

+

+

=

,

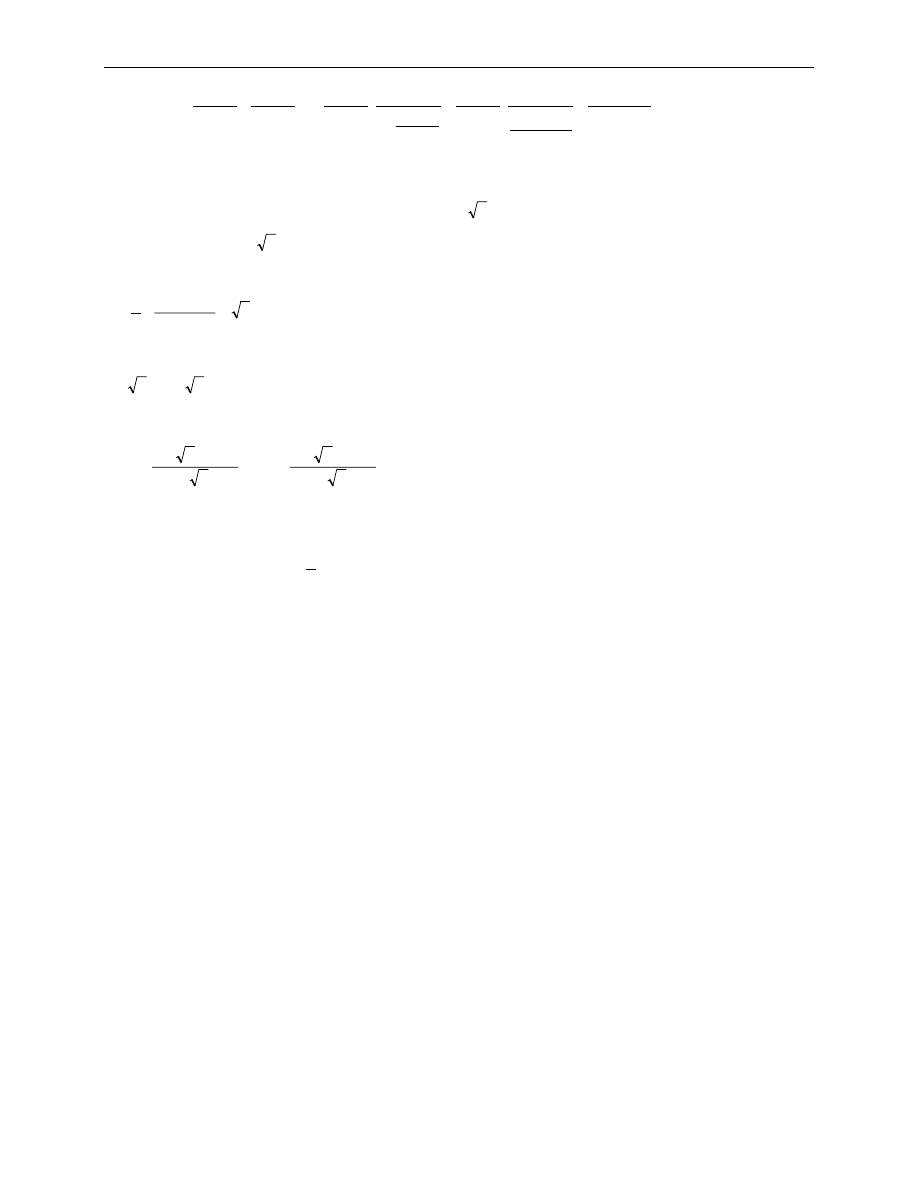
J.Marcinkowski Rachunek rent

5

( )

(

) (

)

(

)

(

)

(

) (

)

(

)

(

)

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

....

1

1

1

1

2

2

2

2

2

2

4

2

−

+

=

+

−

+

⋅

+

=

+

−

⋅

+

=

+

+

+

=

r

r

r

r

r

r

r

r

B

NPV

,

gdzie r jest nieznaną nominalną stopą procentową.

Różnica między bieżącymi wartościami rent ma być równa 2 , skąd otrzymujemy równanie:

( )

( )

2

=

−

B

NPV

A

NPV

.

Wartość r wyznaczamy z równania

( )

2

1

1

1

1

2

=

−

+

−

r

r

.

Po elementarnych przekształceniach otrzymujemy równanie kwadratowe

(

)

0

1

1

2

2

2

2

=

−

−

+

r

r

,

którego pierwiastkami są

(

)

2

2

3

1

2

2

1

−

−

−

=

r

(

)

2

2

3

1

2

2

2

+

−

−

=

r

Pierwszy z nich jest ujemny, drugi dodatni:

4142

,

0

2

=

r

.

Komentarz 1

Wyznaczona w zadaniu wartość

r

1

jest czynnikiem dyskontowania zwykłej renty wieczystej (zob. (6.3.4)). Czynnik

ten pozwala na wyznaczenie funduszu rentowego renty jednostkowej (tj. takiej, której wypłaty są równe jednej
jednostce pieniężnej) dla stopy nominalnej r .

Komentarz 2

Dowodzi się, że równanie

(1)

0

1

...

α

α

α

=

⋅

+

+

⋅

n

n

r

r

,

dla dodatnich

n

i

i

,...,

0

,

0

=

>

α

posiada dokładnie jeden pierwiastek dodatni

*

r

. Równanie może mieć inne

pierwiastki: ujemne lub urojone.

W przypadku gdy (1) jest równaniem stopnia nie wyższego niż trzeci, pierwiastki równania wyznacza się w sposób
analityczny. W przypadku, gdy równanie (1) jest równaniem wyższego stopnia, dodatni pierwiastek znajduje się
stosując metody numeryczne.