Sprawdzenie stateczności środnika w złożonym stanie naprężeń

Środnik projektowanej belki podciągu poddany jest działaniu złożonego stanu

naprężeń. W okolicach maksymalnych momentów zginających w przęsłach pomija się

wpływ sił poprzecznych (naprężeń stycznych) z uwagi na ich niewielkie wartości.

Takiego uproszczenia nie można jednak dokonać w strefach bezpośrednio

sąsiadujących z podporami środkowymi. W tych miejscach momenty zginające i siły

poprzeczne przyjmują bardzo duże, nierzadko maksymalne wartości.

Sprawdzenia stateczności środnika w złożonym stanie naprężeń można dokonać

stosując zależność:



N

w

N

Rw



M

w

M

Rw



P

P

Rc



2

−

3

p



N

w

N

Rw



M

w

M

Rw



P

P

Rc



V

V

R



2



1 .

W powyższej zależności:

N

w

, M

w

, P , V określają obciążenia środnika siłą normalną, momentem

zginającym, siłą skupioną, siłą poprzeczną,

N

Rw

,

M

Rw

,

P

Rc

,

V

R

są nośnościami środnika na ściskanie, zginanie, pod

obciążeniem skupionym i na ścinanie.

W przypadku podciągu, z jakim mamy do czynienia w ćwiczeniu projektowym,

środnik nie jest obciążony siłą osiową N

w

. Wpływ sił skupionych na stateczność

środnika notujemy wtedy, gdy siła ta jest przekazywana przez docisk pasa do

środnika. W naszym przypadku obciążenie jest przekazywane na środnik przez

żebra poprzeczne. W takim razie uwzględnić w obliczeniach należy tylko wpływ

momentów zginających i sił tnących na stateczność środnika.

Przytoczona wcześniej zależność przybiera postać:



M

w

M

Rw



2



V

V

R



2



1 .

Jeśli powyższy warunek jest spełniony środnik pozostaje stateczny. W przeciwnym

wypadku należy zmienić jego parametry lub dodatkowo go usztywnić żebrami.

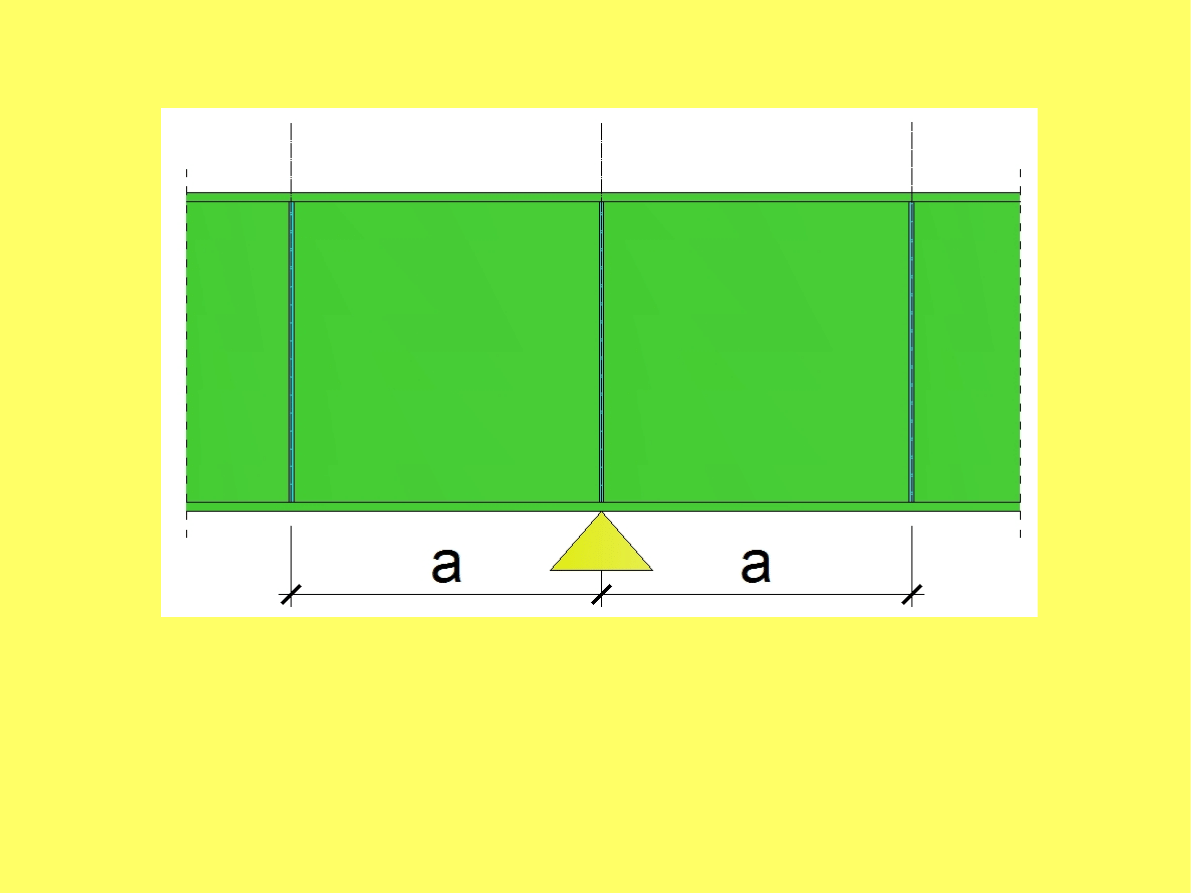
Układ początkowy strefy podporowej

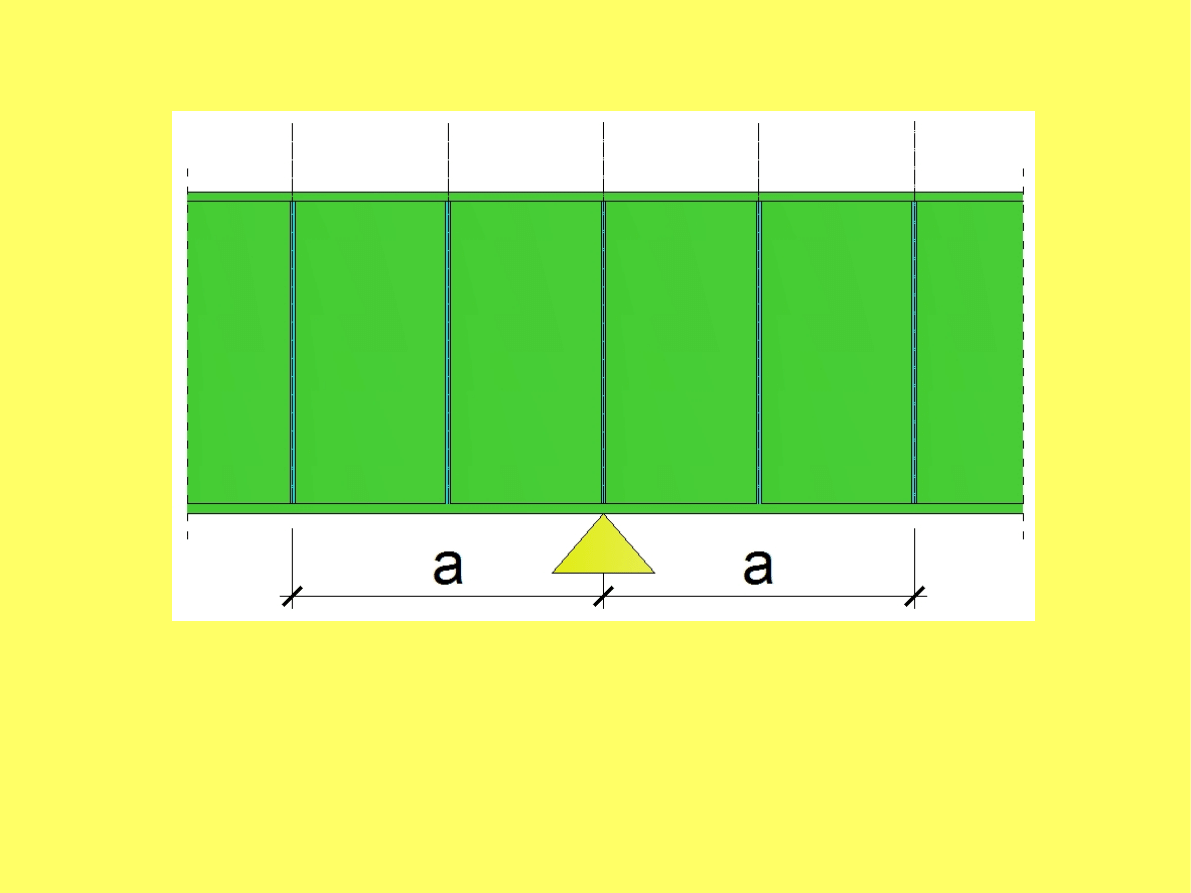
Zagęszczenie żeber poprzecznych (zwiększenie nośności na ścinanie)

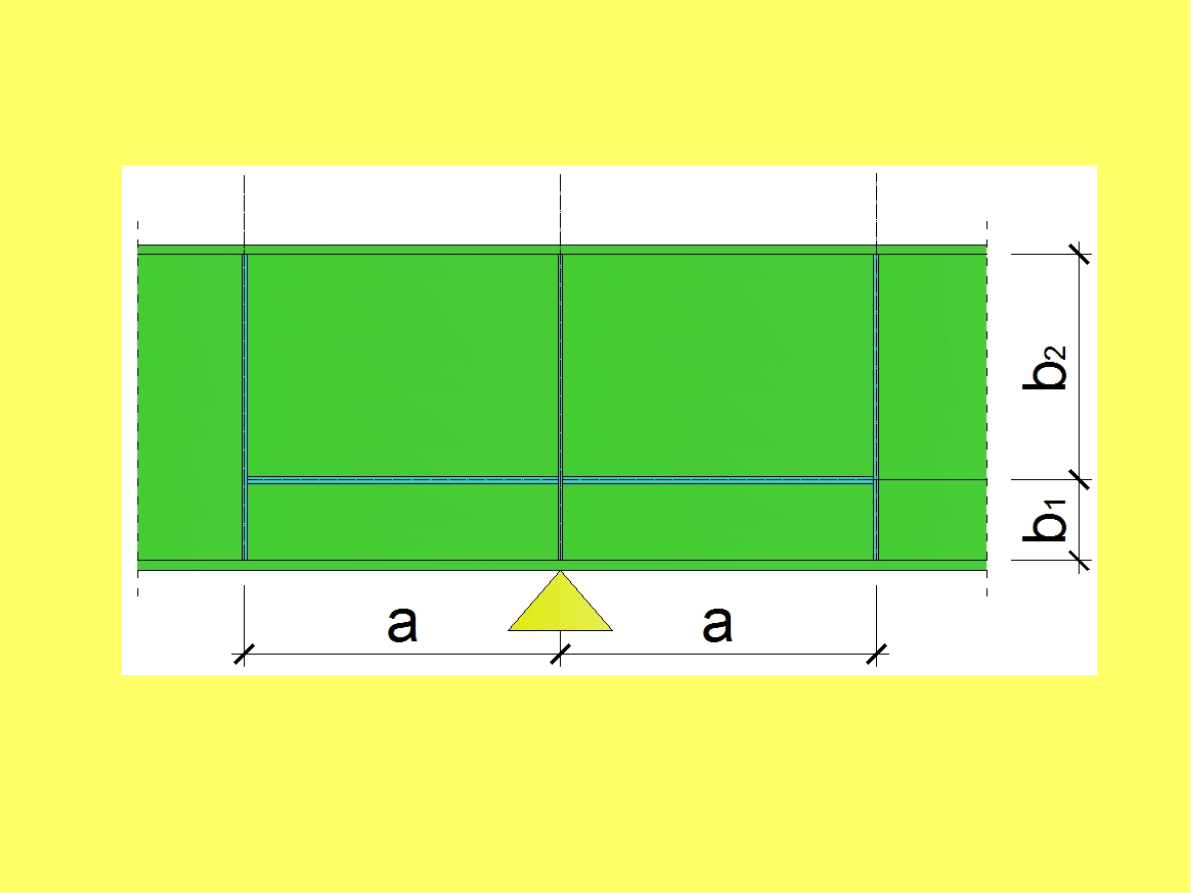
Wprowadzenie żebra podłużnego (zwiększenie nośności środnika na zginanie i

ścinanie jednocześnie)

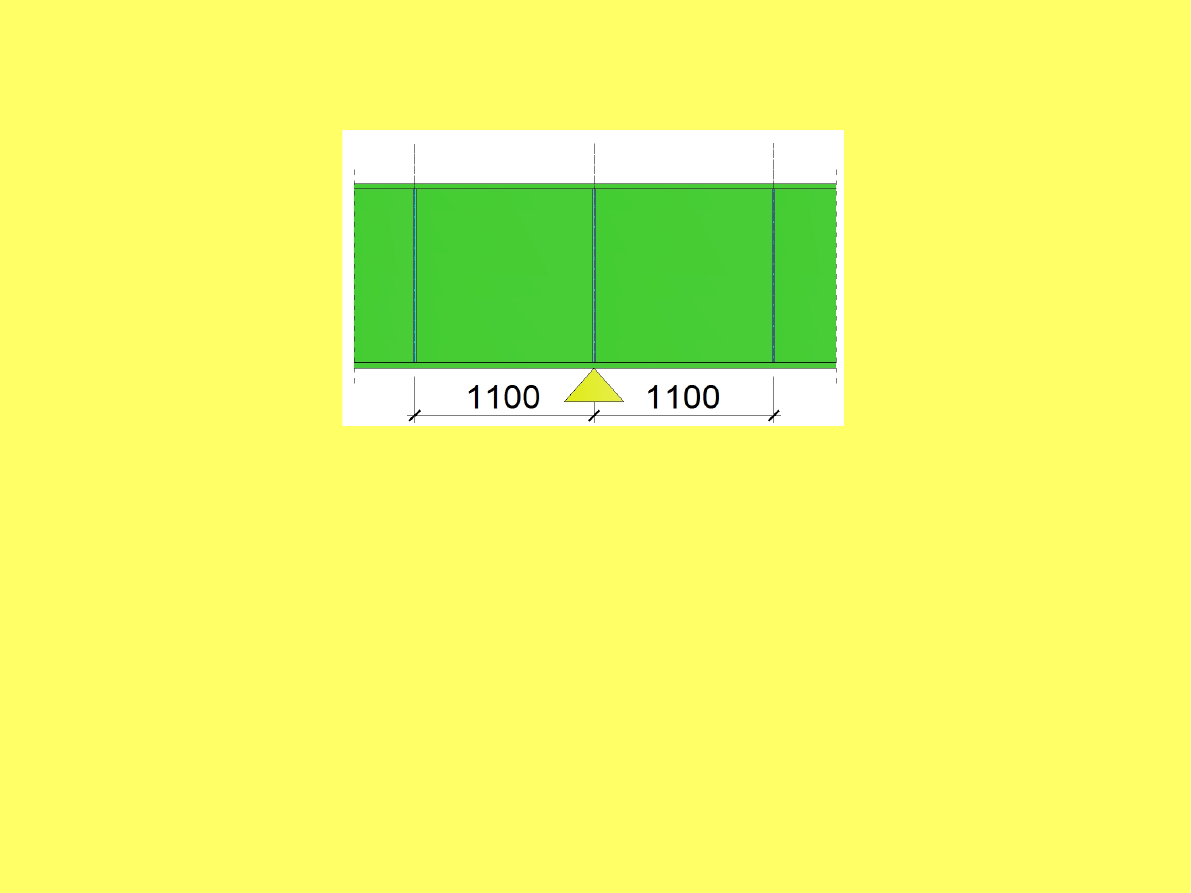
Przykład: Sprawdzenie stateczności środnika w strefie podpory C

Lewa strona podpory C

Moment zginający na podporze C

M

C

=

828,7[kNm] ,

odpowiadająca siła poprzeczna

T

Cl

=

308,6[kN ] .

Cechy geometryczne środnika o wymiarach t

w

×

h

w

=

8×950[mm] .

Moment bezwładności środnika

J

v

=

t

w

h

w

3

12

=

0,8⋅95

3

12

=

57158,3[cm

4

] .

Wskaźnik wytrzymałości środnika

W

xw

=

J

v

h

w

2

=

57158,3

95

2

=

1203,3[cm

3

]

.

Moment zginający obciążający środnik

M

w

=

M

C

J

v

J

xC

=

828,7⋅

57158,3

213291,03

=

222,1[kNm] .

Siła poprzeczna obciążająca środnik

V =T

Cl

=

308,6[ kN ] .

Obliczeniowe nośności środnika

na zginanie: M

Rw

=

w

W

w

f

d

=

0,896⋅1203,3⋅23,5=25342[kNcm]=253,4[ kNm] ,

na ścinanie: V

R

=

0,58

pv

A

v

f

d

=

659,8[kN ] .

Warunek sprawdzający stateczność



M

w

M

Rw



2



V

V

R



2

=

222,1
253,4



2



308,6
659,8



2

=

0,770,22=0,991 .

Prawa strona podpory C

Moment zginający na podporze C

M

C

=

828,7[kNm] ,

odpowiadająca siła poprzeczna

T

Cp

=

352,7[kN ] .

Moment zginający obciążający środnik

M

w

=

M

C

J

v

J

xC

=

828,7⋅

57158,3

213291,03

=

222,1[kNm]

.

Siła poprzeczna obciążająca środnik

V =T

Cp

=

352,7[kN ] .

Obliczeniowe nośności środnika

na zginanie: M

Rw

=



w

W

w

f

d

=

0,896

⋅

1203,3

⋅

23,5

=

25342

[

kNcm

]=

253,4

[

kNm

]

,

na ścinanie: V

R

=

0,58

pv

A

v

f

d

=

659,8

[

kN

]

.

Warunek sprawdzający stateczność



M

w

M

Rw



2



V

V

R



2

=

222,1
253,4



2



352,7
659,8



2

=

0,770,28=1,051 .

Warunek nie został spełniony.

Wymagane jest dodatkowe usztywnienie środnika

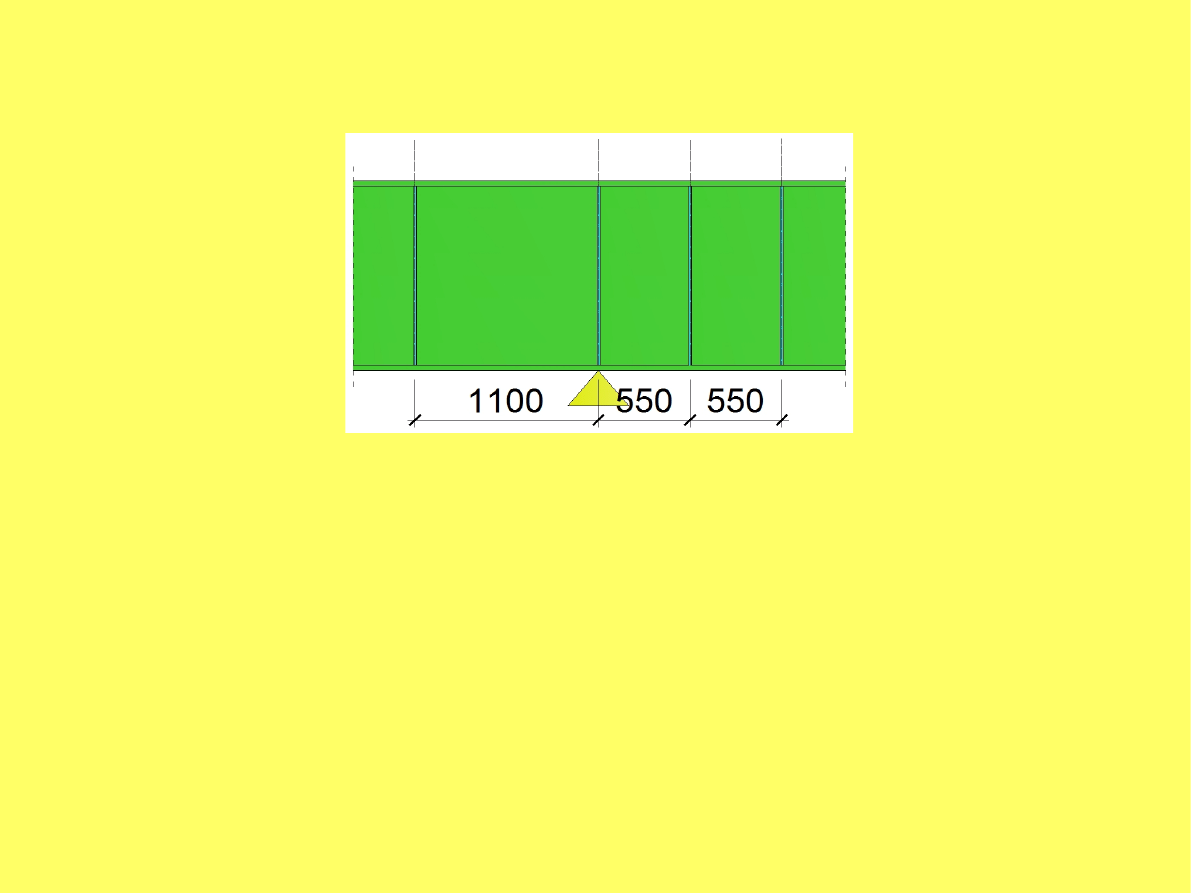
Wariant 1: Zastosowanie tylko żeber poprzecznych (zagęszczenie)

W przypadku zginanego przekroju dwuteowego bisymetrycznego zagęszczenie żeber

poprzecznych takie, że



1

, powoduje jedynie wzrost nośności na ścinanie.

Zagęszczony rozstaw żeber poprzecznych

a

1

=

550[mm] .

Współczynnik rozstawu



1

=

a

1

h

w

=

550
950

=

0,579



1 .

Współczynnik podparcia i obciążenia ścianki ścinanej

K

v

=

0,65 

1



2

−



1

=

0,65

⋅

0,579



2

−

0,579

=

0,449 .

Smukłość płytowa względna



pv

=

b

t

K

v

56



f

d

215

=

950

8

0,449

56



235
215

=

0,995 .

Współczynnik niestateczności miejscowej przy ścinaniu



pv

=

1



pv

=

1

0,995

=

1,006



1





pv

=

1,0 .

Nośność na ścinanie

V

R

=

0,58

pv

A

v

f

d

=

0,58

⋅

1,0

⋅

95,0

⋅

0,8

⋅

23,5

=

1035,9

[

kN

]

Warunek sprawdzający stateczność



M

w

M

Rw



2



V

V

R



2

=

222,1
253,4



2



352,7

1035,9



2

=

0,770,12=0,891 .

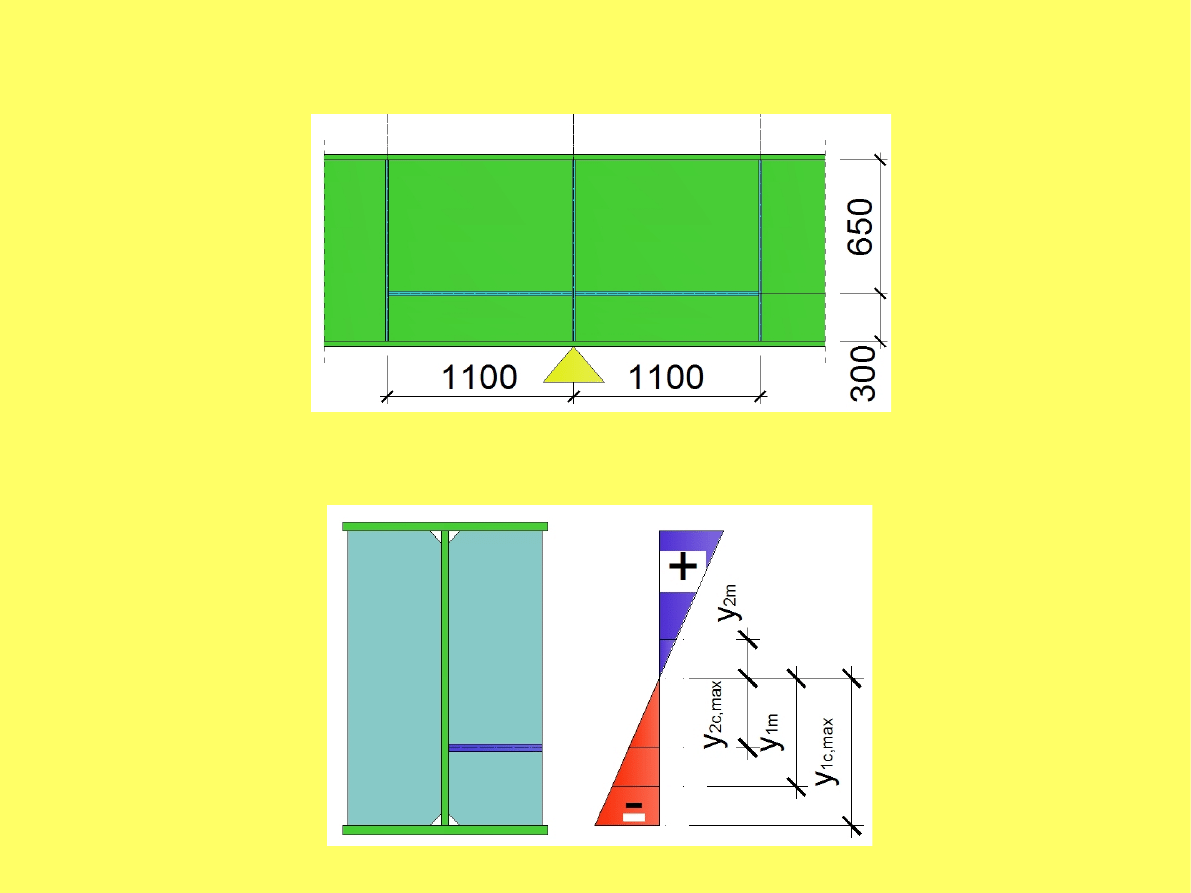
Wariant 2: Zastosowanie żebra podłużnego

Żebro podłużne wprowadzamy w odległości b

1

=

0,25

÷

0,33



h

w

od ściskanej krawędzi

środnika.

b

1

=

0,25÷0,33h

w

=

0,25÷0,33950=238÷317[mm] .

Przyjęto żebro podłużne w odległości b

1

=

300[ mm] .

Parametry statecznościowe płyty dolnej

Współczynnik niestateczności miejscowej przy zginaniu



1

=

a

b

1

=

1100

300

=

3,671

Naprężenia w punktach charakterystycznych płyty dolnej





1

=−

M
J

x



h

w

2

−

b

1

2





c1 , max

=−

M
J

x



h

w

2



=





1



c1 ,max

=

h

w

2

−

b

1

2

h

w

2

=

950

2

−

300

2

950

2

=

325
475

=

0,68

Współczynnik podparcia i obciążenia ścianki

K

2

=

0,40,6=0,40,6⋅0,68=0,811

Smukłość płytowa względna ścianki



p

=

b

1

t

w

K

v

56



f

d

215

=

300

8

0,8

56



235
215

=

0,56



p

=

1,0

Współczynnik niestateczności miejscowej ścianki przy ścinaniu

Współczynnik podparcia i obciążenia ścianki

K

v

=

0,65



2−

1



1

=

0,65



2−

1

3,67

=

0,8540,8

Smukłość płytowa względna ścianki



p

=

b

1

t

w

K

2

56



f

d

215

=

300

8

0,8

56



235
215

=

0,56



pv

=

1



pv

=

1

0,56

=

1,7851



pv

=

1,0

Obliczeniowe nośności środnika

na zginanie: M

Rw

=

w

W

w

f

d

=

1,0⋅1203,3⋅23,5=28278[ kNcm]=282,7[kNm] ,

na ścinanie: V

R

=

0,58

pv

A

v

f

d

=

1035,9[kN ] .

Warunek sprawdzający stateczność



M

w

M

Rw



2



V

V

R



2

=

222,1
282,7



2



352,7

1035,9



2

=

0,620,12=0,741 .

Parametry statecznościowe płyty górnej

Współczynnik niestateczności miejscowej przy zginaniu



2

=

a

b

2

=

1100

650

=

1,6921

Naprężenia w punktach charakterystycznych płyty dolnej





2

=−

M

J

x



h

w

2

−

b

1



b

2

2





c2 , max

=−

M

J

x



h

w

2

−

b

1



=





2



c2 , max

=

h

w

2

−

b

1



b

2

2



h

w

2

−

b

1

=

950

2

−

300

650

2



950

2

−

300

=

150
175

=−

0,857

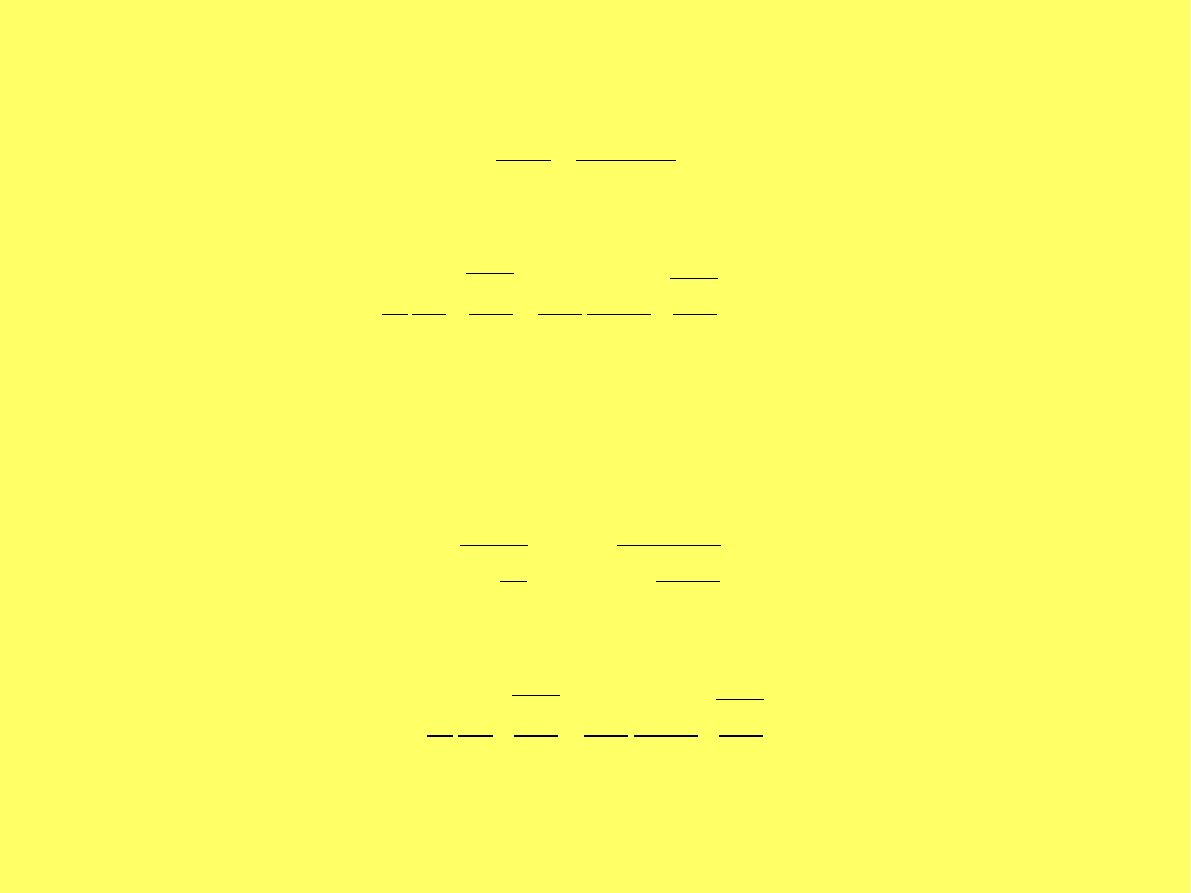
Współczynnik podparcia i obciążenia ścianki

K

2

=

0,4

1−

=

0,4

10,857

=

0,215

Smukłość płytowa względna ścianki



p

=

b

2

t

w

K

2

56



f

d

215

=

650

8

0,215

56



235
215

=

0,3270,75



p

=

1,0

Współczynnik niestateczności miejscowej ścianki przy ścinaniu

Współczynnik podparcia i obciążenia ścianki

K

v

=

0,65



2−

1



2

=

0,65



2−

1

1,692

=

0,7720,8

Smukłość płytowa względna ścianki



pv

=

b

2

t

w

K

2

56



f

d

215

=

650

8

0,772

56



235
215

=

1,17



pv

=

1



pv

=

1

1,17

=

0,8541

Obliczeniowe nośności środnika

na zginanie: M

Rw

=

w

W

w

f

d

=

1,0⋅1203,3⋅23,5=28278[ kNcm]=282,7[kNm] ,

na ścinanie: V

R

=

0,58

pv

A

v

f

d

=

885,1[kN ] .

Warunek sprawdzający stateczność



M

w

M

Rw



2



V

V

R



2

=

222,1
282,7



2



352,7
885,1



2

=

0,620,16=0,781 .

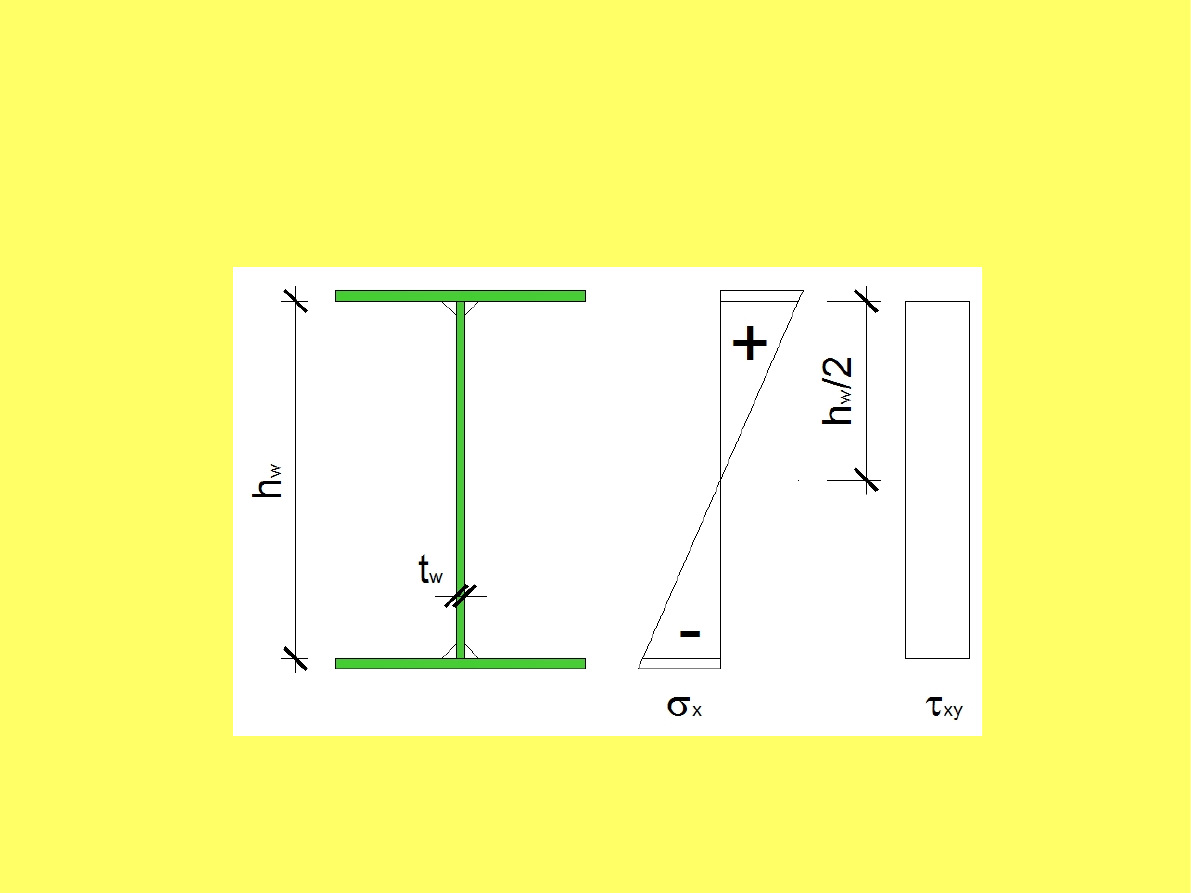
Sprawdzenie warunku naprężeń złożonych

Sprawdzenia dokonujemy w:

●

miejscach występowania znacznych momentów zginających i sił poprzecznych,

●

w miejscach zmiany przekroju.

W przypadku jednokierunkowego zginania ze ścinaniem warunek sprawdzający

zapisujemy następująco:





x

2



3 

xy

2



f

d

.

Naprężenia składowe wyliczamy według zależności:



x

=

M

x

J

x

h

w

2

,



xy

=

V

h

w

t

w

.

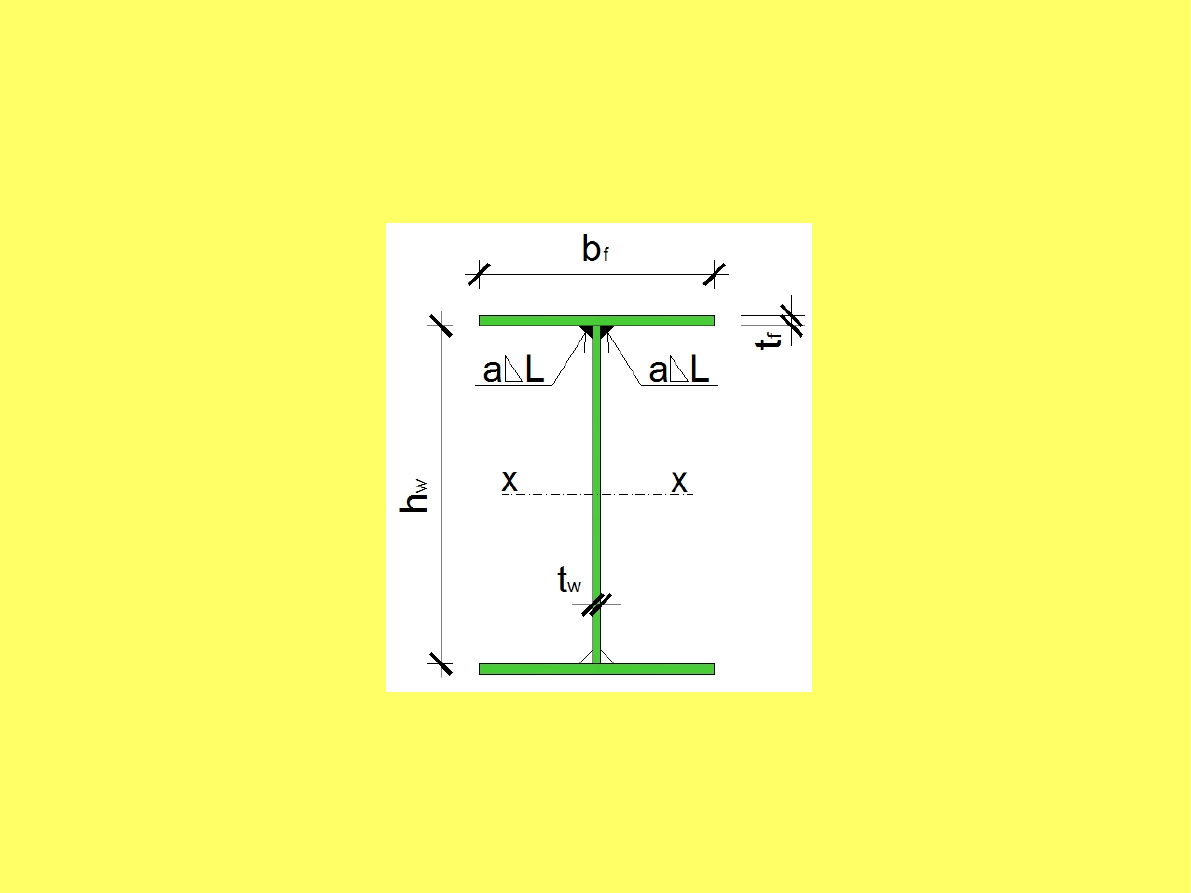
Zwymiarowanie połączenia pasów ze środnikiem

Pasy ze środnikiem łączymy przez spawanie spoinami pachwinowymi ciągłymi lub

przerywanymi, obustronnymi.

Dobór grubości spoiny pachwinowej z warunku konstrukcyjnego:

0,2 t

2



10mm



a



0,7 t

1

2,5 mm

16 mm

,

gdzie:

t

1

- grubość cieńszej z łączonych blach,

t

2

- grubość grubszej z łączonych blach.

Sprawdzenia nośności spoin łączących pasy ze środnikiem dokonujemy z uwagi na

działanie sił rozwarstwiających wywołanych zginaniem



=

V S

x

J

x



a





II

f

d

V

- siła poprzeczna,

S

x

=

b

f

t

f



t

f



h

w

2



- moment statyczny pasa względem osi obojętnej w przekroju,

J

x

- główny centralny moment bezwładności przekroju,



a

- suma grubości spoin łączących pas ze środnikiem.