Całkowanie

Całka jest jednym z najważniejszych pojęć współczesnej analizy matematycznej. Stosuje się ją w

matematyce, fizyce, technice i wielu innych dziedzinach nauki. W matematyce badaniem własności i
obliczaniem wartości całek zajmuje się dział zwany rachunkiem całkowym. Za twórców tego rachunku uważa
się Newtona oraz Leibniza, którzy opracowali teorię i metody związane z pojęciem całki i wprowadzili
terminologię i oznaczenia zbliżone do stosowanych współcześnie, ukazujące związek rachunku całkowego z
rachunkiem różniczkowym.

1.

Całka nieoznaczona

Całką funkcji f(x) będzie każda funkcja F(x), której pochodna jest równa f(x), czyli

F '(x) = f(x)

(1)

Funkcję F(x) nazywamy funkcją pierwotną danej funkcji f(x). Funkcja pierwotna może być znaleziona z
dokładnością do stałej, ponieważ stała znika w trakcie wyznaczania pochodnej. Funkcje pierwotne danej
funkcji f(x) tworzą klasę funkcji różniących się stałymi:

F(x) + C

(2)

Przykład:

Znajdźmy funkcję pierwotną od f(x) = 2x. Korzystamy ze znanego wzoru na pochodną funkcji:

F '(x) = 2x
ponieważ (ax

n

)' = anx

n-1

zatem F '(x) = (x

2

+ C)' = 2x

stąd F(x) = x

2

+ C

Funkcję pierwotną F(x) nazywamy całką nieoznaczoną funkcji f(x) i przedstawiamy:

( )

( )

C

x

F

dx

x

f

+

=

∫

(3)

Zagadnienie obliczania całek nieoznaczonych sprowadza się do znajdowania postaci funkcji pierwotnej co jest
dosyć skomplikowane. W całkowaniu numerycznym głównie zajmujemy się całkami oznaczonymi.

2.

Całka oznaczona

Całka oznaczona funkcji f(x) w przedziale <x

p

,x

k

>

jest liczbą przedstawianą symbolem:

( )

dx

x

f

k

p

x

x

∫

(4)

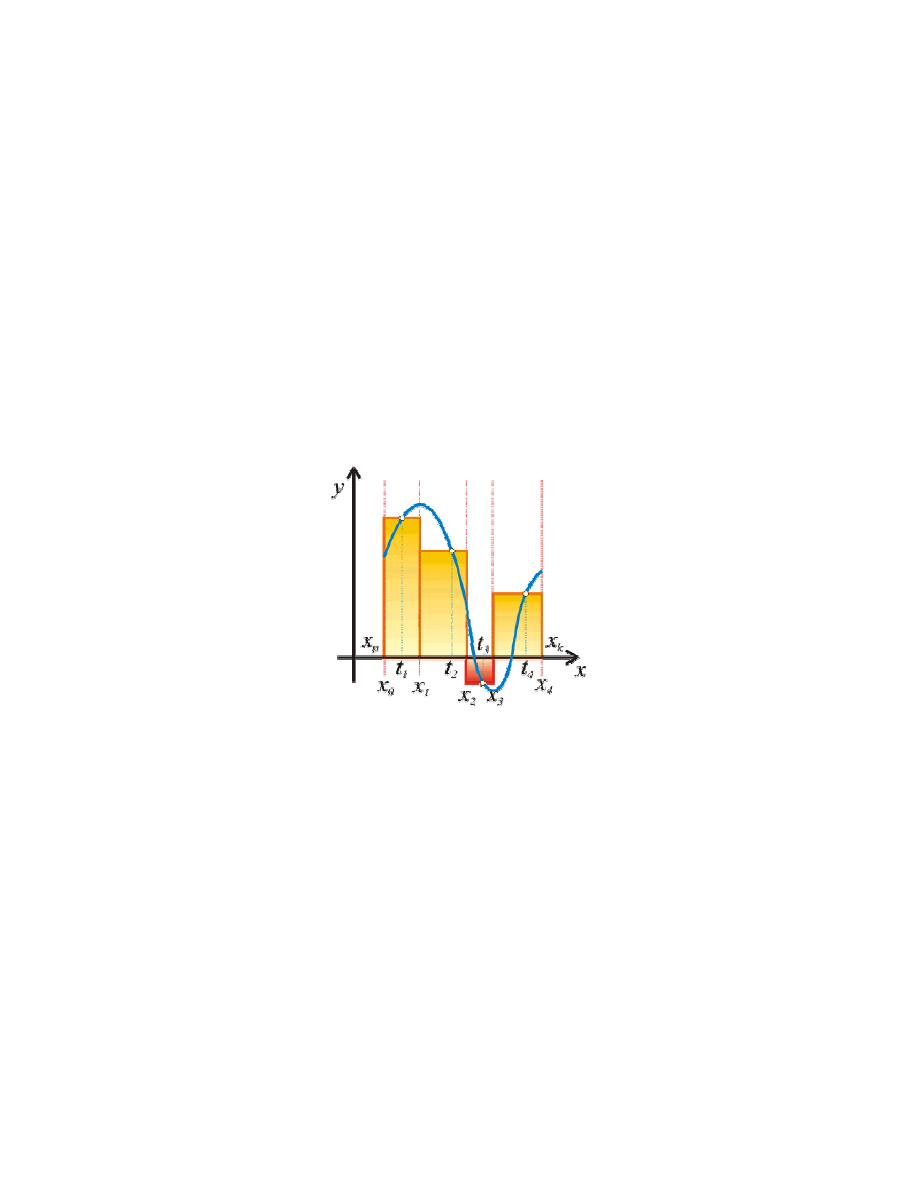
i obliczaną na różne sposoby. Przedział <x

p

,x

k

>

nazywa się przedziałem całkowania. Krańce tego przedziału

nazywa się granicami całkowania. x

p

jest dolną granicą całkowania, a x

k

górną granicą.

Całka oznaczona Newtona-Leibniza

Jeśli znamy przepis na funkcję pierwotną F(x) funkcji podcałkowej f(x), to wartość całki oznaczonej funkcji f(x)
w przedziale <xp,xk> możemy obliczyć w prosty sposób wg definicji Newtona-Leibniza:

( )

( )

( )

p

k

x

x

x

F

x

F

dx

x

f

k

p

−

=

∫

(5)

Z punktu widzenia obliczeń komputerowych sposób ten nie jest najlepszy, ponieważ wymaga wyznaczenia
funkcji pierwotnej F(x), co jest zadaniem numerycznie skomplikowanym - dopiero w ostatnich latach
rozwiązano problem numerycznego wyznaczania wzoru całki dowolnej, całkowalnej funkcji w postaci
analitycznej. Z metody tej korzystają zaawansowane pakiety matematyczne w stylu MathCAD.


Całka oznaczona Riemanna

Większe zastosowanie w obliczeniach numerycznych ma definicja Riemanna, w której całka oznaczona jest
interpretowana jako suma pól obszarów ograniczonych wykresem funkcji f(x) oraz osią OX. Obszary leżące
pod osią mają w tej interpretacji pola ujemne.

Przedział całkowania <xp,xk> dzielimy na rozłączne podprzedziały wyznaczając n+1 punktów podziałowych:

x

p

= x

o

< x

1

< ... < x

n-1

< x

n

= x

k

Punkty podziałowe muszą być tak dobrane, aby przy wzroście n do nieskończoności maksymalna odległość
między sąsiednimi punktami malała do zera, czyli:

dla i = 1, 2, ..., n

(

)

0

max

lim

1

=

−

−

∞

→

i

i

n

x

x

Pomiędzy parami sąsiednich punktów x

i-1

i x

i

wybieramy dowolne punkty t

i

spełniające nierówność:

dla i = 1, 2, ..., n

x

i-1

< t

i

< x

i

Całka oznaczona Riemanna jest wtedy granicą sum n prostokątów o podstawie równej (x

i

- x

i-1

) i wysokości

f

(t

i

), czyli

( )

( )(

)

1

1

lim

−

=

∞

→

−

=

∑

∫

i

i

n

i

i

n

x

x

x

x

t

f

dx

x

f

k

p

(6)

Jeśli f(t

i

) jest mniejsze od zera, to pole tego prostokąta zostanie zsumowane ze znakiem minus. Gdy odległości

pomiędzy punktami podziałowymi zbliżają się do zera, suma pól prostokątów dąży do pola obszaru
ograniczonego wykresem funkcji.

Różnicę pomiędzy wartością pola pod wykresem funkcji a polem otrzymanym jako suma skończonej ilości
prostokątów nazywamy błędem całkowania. Wraz ze wzrostem liczby prostokątów w całce Riemanna błąd
całkowania dąży do zera.

3.

Metody numeryczne całkowania

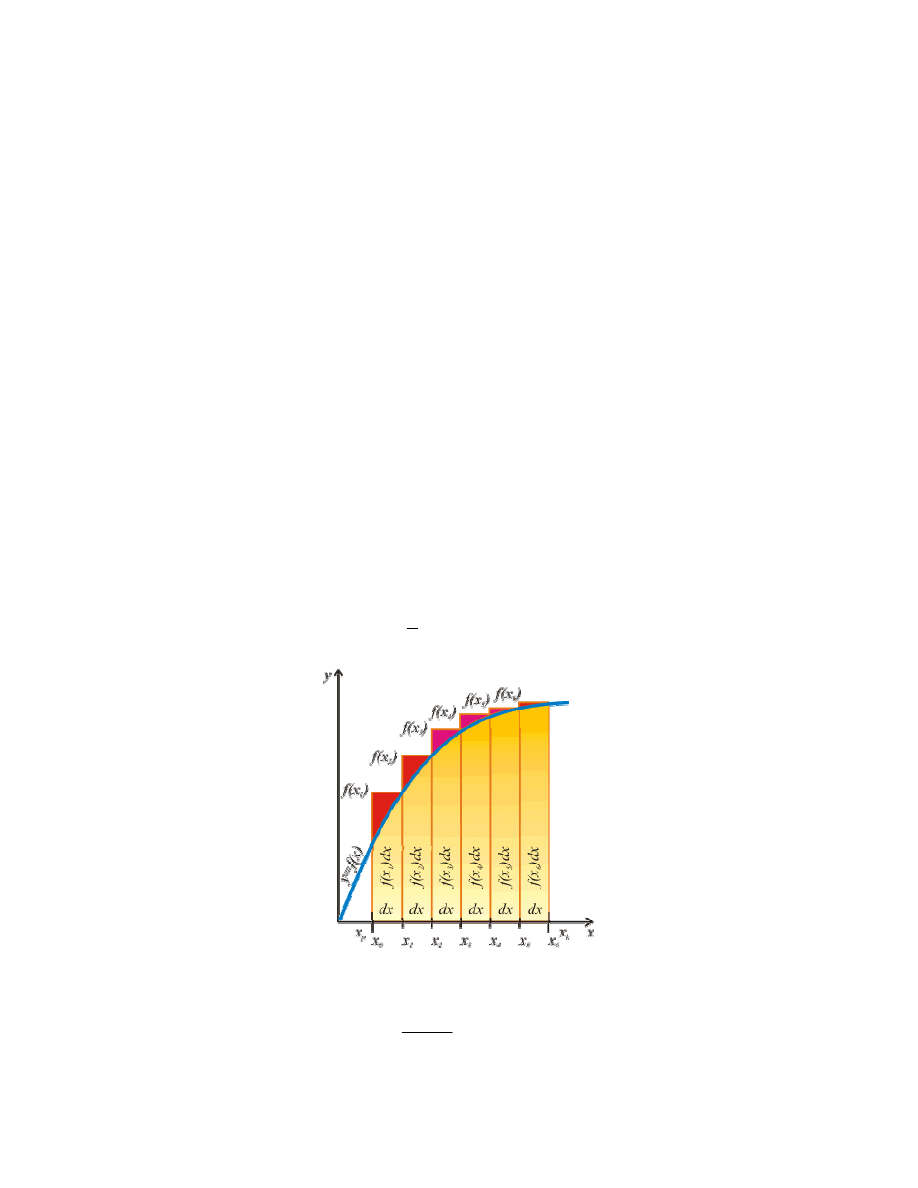
Metoda prostokątów

W metodzie prostokątów korzystamy z definicji całki oznaczonej Riemanna, w której wartość całki

interpretowana jest jako suma pól obszarów pod wykresem krzywej w zadanym przedziale całkowania <x

p

,x

k

>

.

Sumę tę przybliżamy przy pomocy sumy pól odpowiednio dobranych prostokątów. Sposób postępowania jest
następujący:
Przedział całkowania <x

p

,x

k

>

dzielimy na n równo odległych punktów x

1

,x

2

,...,x

n

. Punkty te wyznaczamy w

prosty sposób wg wzoru:

dla i = 1,2,...,n

(

)

p

k

p

i

x

x

n

i

x

x

−

+

=

(7)

Obliczamy odległość między dwoma sąsiednimi punktami - będzie to podstawa każdego prostokąta:

n

x

x

dx

p

k

−

=

(8)

Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

f

i

= f(x

i

),

dla i = 1,2,...,n

(9)

Obliczamy sumę iloczynów wyznaczonych wartości funkcji przez odległość dx między dwoma sąsiednimi
punktami - da to sumę pól poszczególnych prostokątów ograniczonych wykresem funkcji:

S = f

1

dx + f

2

dx + ... + f

n

dx

(10)

a po wyprowadzeniu wspólnego czynnika przed nawias:

S = dx (f

1

+ f

2

+ ... + f

n

)

(11)

Otrzymana suma jest przybliżoną wartością całki oznaczonej funkcji f(x) w przedziale <x

p

,x

k

>

.

( )

∑

∫

=













−

+

−

≈

n

i

p

k

p

x

x

p

k

n

x

x

i

x

f

n

x

x

dx

x

f

k

p

1

(12)

Przykład:
Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) = sin(x)

w przedziale <0,π>.

Przedział podzielimy na n = 4 punkty:

Odległość między dwoma sąsiednimi punktami wynosi:

Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) = sin(x):

Obliczamy sumę pól prostokątów:

S

= dx (f

1

+ f

2

+ f

3

+ f

4

)

S

= 0,7854 (0,7071 + 1,000 + 0,7071 + 0,0000)

S

= 0,7854 × 2,4142

S

= 1,8961

Dokładna wartość takiej całki oznaczonej wynosi wg tablic:

∫

=

π

0

2

sin xdx

Zatem popełniliśmy błąd równy: 2 - 1,8961 = 0,1039, co stanowi nieco ponad 5% wartości dokładnej. W sumie
nie jest to zły wynik zważywszy na ilość wykonanych przez nas rachunków. Jeśli chcemy zwiększyć
dokładność, to musimy zsumować więcej prostokątów, ale to zostawimy już komputerom.

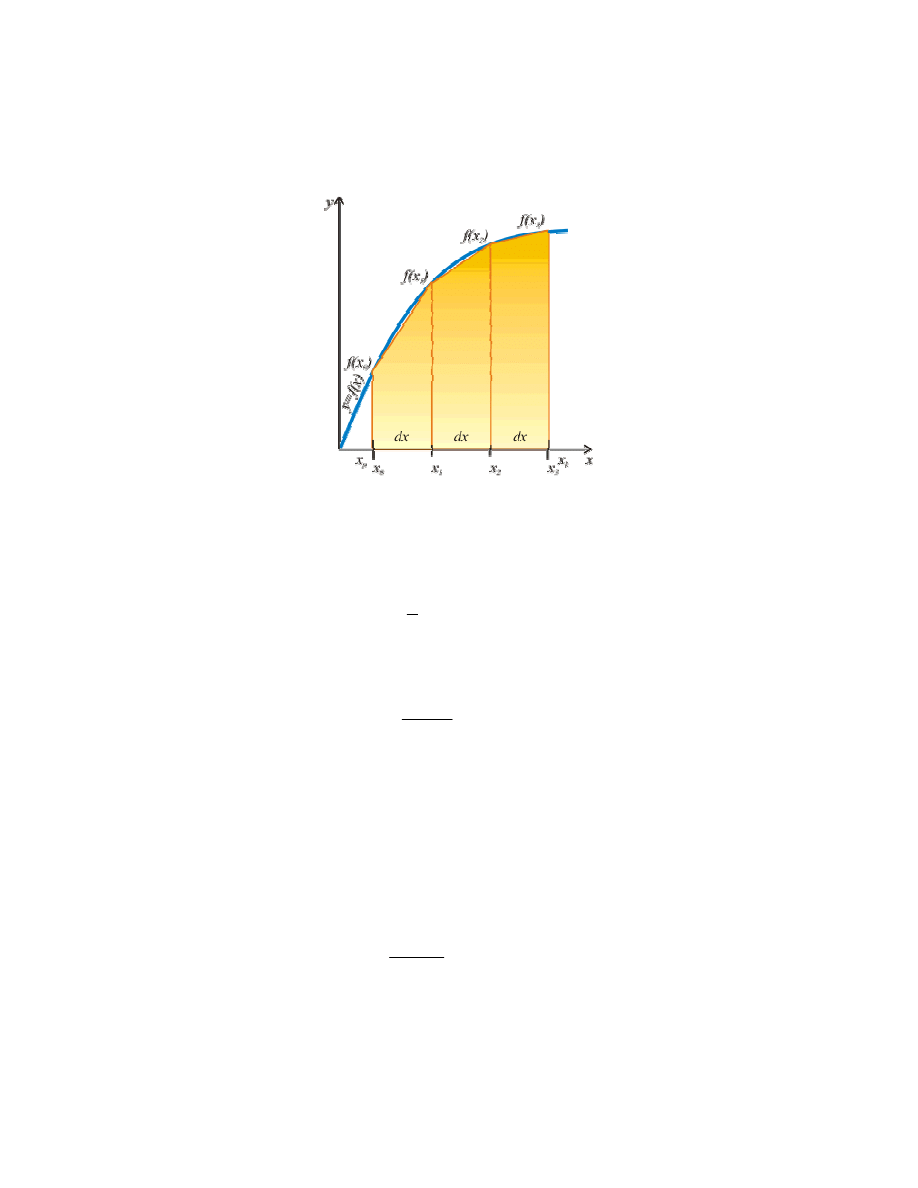
Metoda trapezów

Metoda prostokątów nie jest zbyt dokładna, ponieważ pola użytych w niej prostokątów źle

odwzorowują pole pod krzywą. Dużo lepszym rozwiązaniem jest zastosowanie zamiast nich trapezów o
wysokości dx i podstawach równych odpowiednio wartości funkcji w punktach krańcowych.. Sama zasada nie
zmienia się.

Przedział całkowania <x

p

,x

k

>

dzielimy na n równo odległych punktów x

1

,x

2

,...,x

n

. Punkty te wyznaczamy w

prosty sposób wg wzoru:

dla i = 0,1,2,...,n

(

)

p

k

p

i

x

x

n

i

x

x

−

+

=

(13)

Obliczamy odległość między dwoma sąsiednimi punktami - będzie to wysokość każdego trapezu:

n

x

x

dx

p

k

−

=

(14)

Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

f

i

= f(x

i

),

dla i = 0,1,2,...,n

(15)

Pole pod wykresem funkcji przybliżane jest polami n trapezów. Pole i-tego trapezu obliczamy wg wzoru:

dla i=1,2,...,n

dx

f

f

P

i

i

i

2

1

+

=

−

(16)

Przybliżona wartość całki jest sumą pól wszystkich otrzymanych w ten sposób trapezów:

s = P

1

+ P

2

+ ... + P

n

(17)

czyli

(

)

(

)

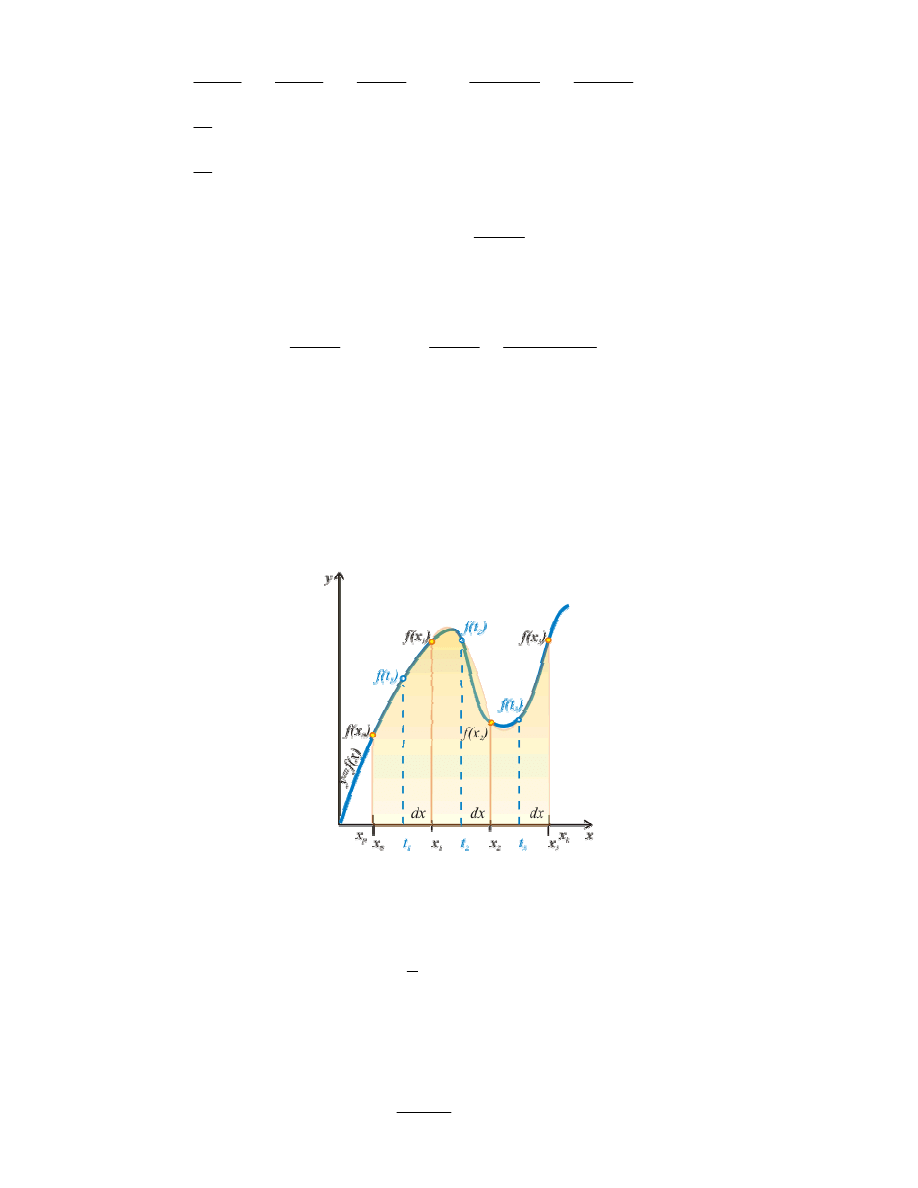
n

n

n

n

n

n

n

n

n

n

f

f

f

f

f

dx

s

f

f

f

f

f

f

f

f

f

f

dx

s

dx

f

f

dx

f

f

dx

f

f

dx

f

f

dx

f

f

s

+

+

+

+

+

=

+

+

+

+

+

+

+

+

+

+

=

+

+

+

+

+

+

+

+

+

+

=

−

−

−

−

−

−

−

1

2

1

0

1

1

2

3

2

2

1

1

0

1

1

2

3

2

2

1

1

0

2

2

2

2

2

2

2

2

2

2

K

K

K

(18)













+

+

+

+

+

=

−

2

0

1

2

1

n

n

f

f

f

f

f

dx

s

K

(19)

Wyprowadzony na końcu wzór jest podstawą przybliżonego wyliczania całki w metodzie trapezów.

( )

( )

( )















+

+













−

+

−

≈

∑

∫

−

=

2

1

1

k

p

n

i

p

k

p

p

k

x

x

x

f

x

f

n

x

x

i

x

f

n

x

x

dx

x

f

k

p

(20)

Metoda Simpsona

Metoda ta jest dokładniejsza od opisanych tutaj metod przybliżonego całkowania. W metodzie

prostokątów całka oznaczona przybliżana była funkcjami stałymi - liczyliśmy sumę pól prostokątów. W
metodzie trapezów całkę przybliżaliśmy za pomocą funkcji liniowych - obliczaliśmy sumy pól trapezów. W
metodzie Simpsona stosujemy jako przybliżenie parabolę - będziemy obliczali sumy wycinków obszarów pod
parabolą.

Zasada jest następująca:
Przedział całkowania <x

p

,x

k

>

dzielimy na n + 1 równo odległych punktów x

o

, x

1

, x

2

,..., x

n

:

dla i = 0,1,2,...,n

(

)

p

k

p

i

x

x

n

i

x

x

−

+

=

(21)

Dla każdych dwóch sąsiednich punktów wyznaczamy punkt środkowy t

i

wg wzoru:

dla i = 1,2,...,n

2

1

i

i

i

x

x

t

+

=

−

(22)

Obliczamy odległość między dwoma sąsiednimi punktami.

n

x

x

dx

p

k

−

=

(22)

Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:

punkty podziałowe:

dla i = 0,1,2,...,n

f

i

= f(x

i

)

(23)

punkty środkowe:

dla i = 1,2,...,n

f

ti

= f(t

i

)

(24)

W każdym podprzedziale <x

i-1

,x

i

>

przybliżamy funkcję za pomocą paraboli g(x) o następującej postaci:

dla i = 1,2,...,n

( )

i

i

i

i

i

i

x

x

x

c

x

b

x

a

x

g

,

1

2

−

∈

+

+

=

(25)

Parabola g

i

(x)

musi przechodzić przez punkty: (x

i-1

,f

i-1

), (t

i

,f

ti

), (x

i

,f

i

). Współczynniki a

i

, b

i

i c

i

wyznaczymy

zatem z układu trzech równań:

dla i = 1,2,...,n

i

i

i

i

i

i

ti

i

i

i

i

i

i

i

i

i

i

i

f

c

x

b

x

a

f

c

t

b

t

a

f

c

x

b

x

a

=

+

+

=

+

+

=

+

+

−

−

−

2

2

1

1

2

1

(26)

Po przekształceniach otrzymujemy:

dla i = 1,2,...,n

( )

(

)

(

)

ti

i

i

x

x

p

k

i

f

f

f

n

x

x

dx

x

g

i

i

4

6

1

1

+

+

−

=

−

∫

−

(27)

Wzór ten pozwala wyliczyć pole obszaru pod parabolą aproksymującą funkcję f(x) w przedziale <x

i-1

,x

i

>.

Wartość całej całki otrzymamy sumując te pola, czyli:

( )

(

)













+

+

−

=

∑

∑

∑

∫

=

=

=

−

−

n

i

i

n

i

ti

n

i

i

x

x

p

k

f

f

f

n

x

x

dx

x

f

i

i

1

1

1

1

4

6

1

(28)

4.

Całkowanie w matlab / octave

Problem polega na znalezieniu całki oznaczonej funkcji f(x) na przedziale <a,b>. Jest to łatwe, gdy znana jest
funkcja pierwotna F(x) taka, że F(x)’=f(x) . Nie zawsze jest to jednak możliwe. Metody całkowania
numerycznego (kwadratury) polegają na przybliżeniu funkcji podcałkowej f na danym przedziale <a,b> lub
jego podprzedziałach przy pomocy innej funkcji, dla której wartość całki jest określona analitycznie. Matlab
stosuje kwadratury Newtona-Cotesa - quad (interpolacja wielomianem drugiego stopnia) i Simpsona -
quadl

(interpolacja wielomianowa – dobierany stopień wielomianu).

Q=quad(f,a,b,tol,trace);
Q=quadl(f,a,b,tol,trace);

f

– łańcuch zawierający nazwę funkcji, funkcja musi być umieszczona w odpowiednim skrypcie, musi

zwracać wektor wartości a jej argumentem jest wektor elementów.
a,b

– przedział całkowania,

tol

– wymagana tolerancja względna, domyślnie 10^(-3)

trace

– parametr opcjonalny, pozwala na rysowanie wykresu z węzłami kwadratury.

Przykład:
function [y] = funkcja_calkowana(x)
%% funkcja
y=sin(x.*x);
end

Wywołanie funkcji całkowania
>> q1 = quad(‘funkcja_calkowana’,0,pi,1e-5,1);
>> ql = quadl(‘funkcja_calkowana’,0,pi,1e-5,1);

Funkcja trapz – całkowanie metodą trapezów
Przykład:
>> x=linspace(0,pi,100);
>> y=sin(x);
>> trapz(x,y)

5.

Ćwiczenia:

5.1.

Zdefiniuj funkcję y=x

2

+2x+1

w pliku f1.m

5.2.

Utwórz skrypt main5.m w którym określ:

•

początek i koniec przedziału całkowania <-1,1> pod zmiennymi x

p

, x

k

•

ilość podprzedziałów całkowania jako 3 pod zmienną n

•

narysuj funkcję podcałkową w przedziale całkowania – kolor czerwony

5.3.

Uzupełnij podprogram f_rectI.m reprezentujący metodę prostokątów według wskazówek zawartych

wewnątrz pliku. Z plikami f_trapI (metoda trapezów) oraz f_SimpI (metoda Simpsona) należy postąpić
analogicznie – wskazówki oraz odniesienia do wzorów określających daną metodę są komentarzami wewnątrz
plików.

5.4.

W programie main5.m wywołaj wymienione funkcje z parametrami w kolejności:

(funkcja całkowana, x

p

, x

k

, n)

5.5.

Porównaj wyniki wszystkich metod dla różnych n: np. 3, 7, 10

5.6.

Wykorzystaj funkcje wbudowane (quad, quadl, trapz) do obliczenia całki funkcji f1

5.7.

Porównaj wyniki, sprawdź wpływ parametru tol