Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 1 z 8
....................................
kod pracy ucznia
.............................................
pieczątka WKK
KONKURS PRZEDMIOTOWY MATEMATYCZNY
DLA UCZNIÓW GIMNAZJÓW
ETAP WOJEWÓDZKI
Drogi Uczniu
Witaj na II etapie konkursu matematycznego. Przeczytaj uważnie instrukcję i postaraj się
prawidłowo odpowiedzieć na wszystkie pytania.
• Arkusz liczy 8 stron i zawiera 18 zadań oraz załącznik w formie
brudnopisu.
• Przed
rozpoczęciem pracy sprawdź czy Twój test jest kompletny.
Jeżeli zauważysz usterki, zgłoś je Komisji Konkursowej.
• Zadania czytaj uważnie i ze zrozumieniem.
• Odpowiedzi wpisuj czarnym lub niebieskim długopisem bądź
piórem.
• Dbaj o czytelność pisma i precyzję odpowiedzi.
• Nie
używaj korektora. Jeśli się pomylisz przekreśl błędną
odpowiedź i wpisz poprawną.
• W przypadku testu wyboru (zadania od 1 do 12) prawidłową
odpowiedź zaznacz stawiając znak X na literze poprzedzającej
treść wybranej odpowiedzi. Jeżeli pomylisz się, błędne
zaznaczenie otocz kółkiem i zaznacz znakiem X inną odpowiedź.
• W zadaniach otwartych (zadania od 13 do18) przedstaw tok
rozumowania prowadzący do wyniku (uzasadnienia odpowiedzi).
• Oceniane
będą tylko odpowiedzi, które zostały umieszczone
w miejscu do tego przeznaczonym.
• Nie
używaj kalkulatora.
• Przy
rozwiązywaniu zadań możesz korzystać z przyborów
kreślarskich.
• Przy
każdym zadaniu podano maksymalną liczbę punktów
możliwą do uzyskania za jego rozwiązanie.
Pracuj samodzielnie.
Powodzenia!
Czas pracy:
90 minut
Liczba punktów
możliwych
do uzyskania:
50
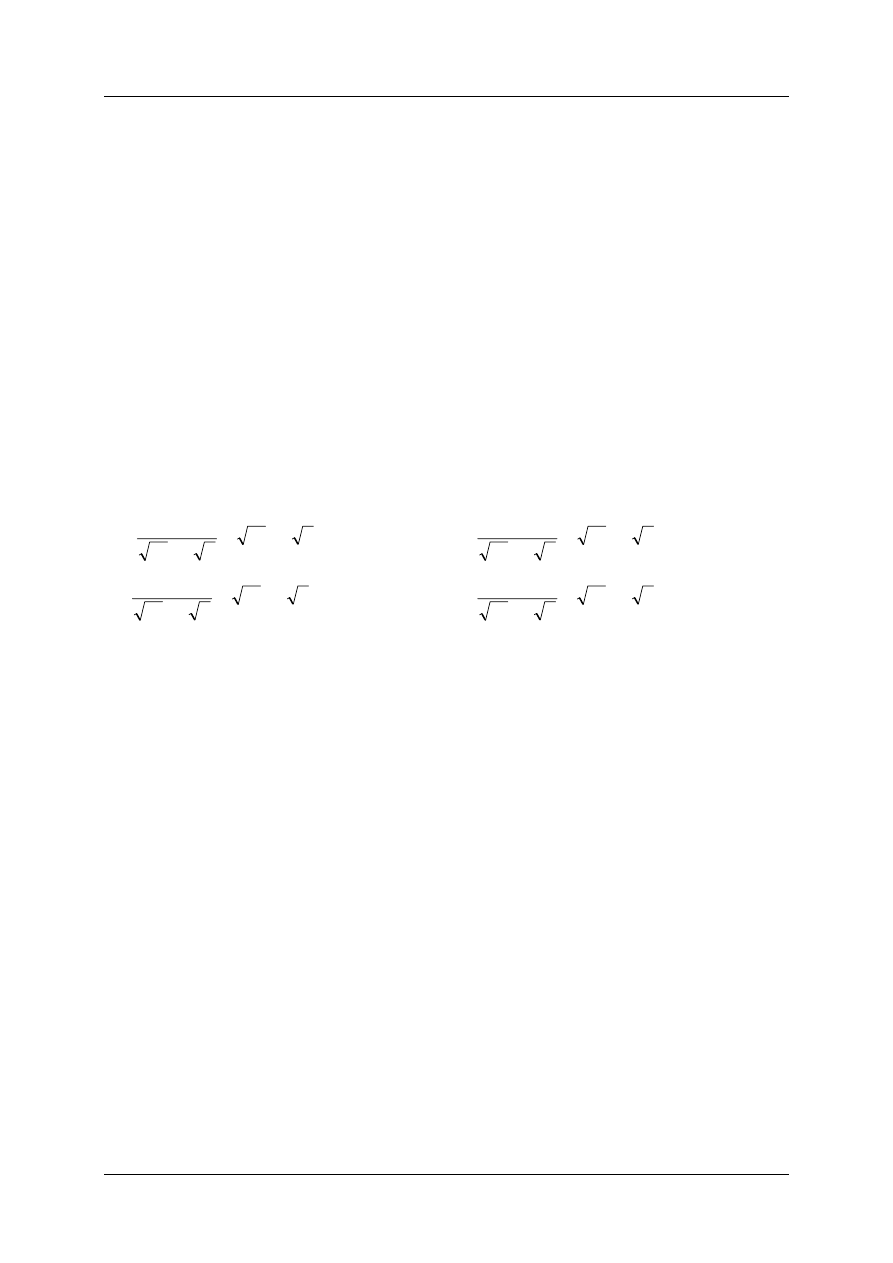
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 2 z 8
Zadanie 1 (0-1 pkt.)
Ile liczb dwucyfrowych o różnych cyfrach można uzyskać z cyfr: 0,1,2,3,4?
A. 25
B. 10
C. 16
D. 20
Zadanie 2 (0-1 pkt.)
Dla jakiej liczby k funkcja
( ) (
)
5
2
2
+
−
=
x
k
x
f
spełnia warunek
( )
1
2
=
−
f
A. 1
B. 2
C. -2
D. 0
Zadanie 3 (0-1 pkt.)
Który z podanych związków jest prawdziwy? (Który zapis jest prawdziwy?)
A.
2
3
19
2
3
19
1
+
=
−
C.
2
3
19
2
3
19
1
−
>
−
B.
2
3
19
2
3
19
1
+
>
−
D.
2
3
19
2
3
19
1
+
<
−
Zadanie 4 (0-1 pkt.)
Doprowadzając wyrażenie
(
) (
)
2
2
n
n
n
n
q
p
q
p
+
−
−
do prostszej postaci otrzymamy:
A.
n
n
q
p
4
B.
(
)
n
n
q
p
2
2
2
−
C.
(
)
n
n
q
p
2
2
2
+
−
D.
n
n
q
p
4
−
Zadanie 5 (0-1 pkt.)
Model budynku wykonany w skali 1:50 ma objętość 0,2 m
3
. Objętość tego
budynku wynosi:
A. 10m
3
B. 25000m
3
C. 500m
3
D. 125000m
3
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 3 z 8
Zadanie 6 (0-2 pkt.)
Samochód wyjechał z miasta P w południe z prędkością 90 km/h. O której
godzinie dogoni rowerzystę, który wyruszył z tego samego miejsca o siódmej
rano i jedzie z prędkością 15 km/h?
A. po 12
00
lecz przed 12
30
B. o 12
30
C. po 12
30
lecz przed 13
00
D. o 13
00
Zadanie 7 (0-2 pkt.)
Jeden bok prostokąta zwiększono o 25%. O ile procent należy zmniejszyć drugi
bok prostokąta, by pole nie zmieniło się?
A. 25%
B. 20%
C. 80%
D. 75%
Zadanie 8 (0-2 pkt.)
Jaka jest cyfra jedności liczby 2003
2001
+ 2007
2000
+ 2009
1999
?
A. 3
B. 7
C. 9
D. 1
Zadanie 9 (0-2 pkt.)
Trapez i romb mają wysokości równej długości. Długość boku rombu jest dwa
razy większa od długości krótszej podstawy trapezu. Pole trapezu jest trzy razy
większe od pola rombu. Stosunek długości dłuższej podstawy trapezu do boku
rombu wynosi:
A. 5:1
B. 5:2
C. 11:1
D. 11:2
Zadanie 10 (0-2 pkt.)
Jeśli w pewnej liczbie skreślimy ostatnią cyfrę wynoszącą 8, to liczba
zmniejszy się o 25613. Szukana liczba to:
A. 256138
B. 28458
C. 256128
D. 28548
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 4 z 8
Zadanie 11 (0-2 pkt.)
Stary zegar spóźnia się 8 minut na dobę. O ile trzeba go posunąć w przód
wieczorem o 22
00
, aby następnego ranka o godzinie 7
00
wskazywał dokładny
czas?
A. o 1 min. i 40 sek. B. o 2 min. i 20 sek. C. o 3 min.
D. o 4 min.
Zadanie 12 (0-3 pkt.)
Gdyby Aleksander Wielki umarł o 5 lat wcześniej panowałby
4
1
swego życia,
gdyby zaś żył o 9 lat dłużej, panowałby połowę swego życia. Aleksander
panował:
A. 12 lat
B. 33 lata
C. 14 lat
D. 38 lat
ZADANIA OTWARTE
Zadanie 13 (0- 4 pkt.)
Świeżo zerwany arbuz zawierający 97,5% wody ważył 7 kg. Po pewnym czasie
arbuz wysechł i zawartość wody spadła do 96%. Ile teraz waży arbuz?
Odpowiedź
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 5 z 8
Zadanie 14 (0-5 pkt.)
Proste
k
mx
y
−
=
i
m
kx
y
3
8
+
=
przecinają się w punkcie A(10,14). Oblicz pole
figury ograniczonej wykresami tych prostych i osią OY.
Odpowiedź
Zadanie 15 (0-5 pkt.)
Jurek wybrał się na wycieczkę rowerową. Całą trasę podzielił na dwa odcinki
równej długości. Pierwszy odcinek pokonał z prędkością 30 km/h, a całą trasę
ze średnią prędkością 24 km/h. Oblicz, z jaka prędkością przejechał drugi
odcinek trasy. (Prędkością średnią nazywamy stosunek przemieszczenia do
czasu, w jakim to przemieszczenie nastąpiło).
Odpowiedź
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 6 z 8
Zadanie 16 (0-5 pkt.)
Długości krawędzi prostopadłościanu, wyrażone w centymetrach są liczbami
naturalnymi. Jedna ze ścian ma pole 18 cm
2
a druga 45 cm
2
. Jakie wymiary
może mieć ten prostopadłościan? (Podaj wszystkie rozwiązania).
Odpowiedź
Zadanie 17. (0-4 pkt.)
Udowodnij, że w dowolnym trójkącie prostokątnym suma przyprostokątnych
jest równa sumie średnic okręgów wpisanego i opisanego na tym trójkącie.
Odpowiedź
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 7 z 8
Zadanie 18. (0 - 7 pkt.)
Przekrój osiowy stożka jest trójkątem równobocznym, przekrój walca
wpisanego w stożek jest kwadratem o polu 36 cm
2
. Oblicz stosunek objętości
walca do objętości stożka.
Odpowiedź
Konkursy w województwie podkarpackim w roku szkolnym 2005/2006
Strona 8 z 8
BRUDNOPIS