.

METODY WYMIAROWANIA KONSTRUKCJI METALOWYCH

Wiadomości wstępne

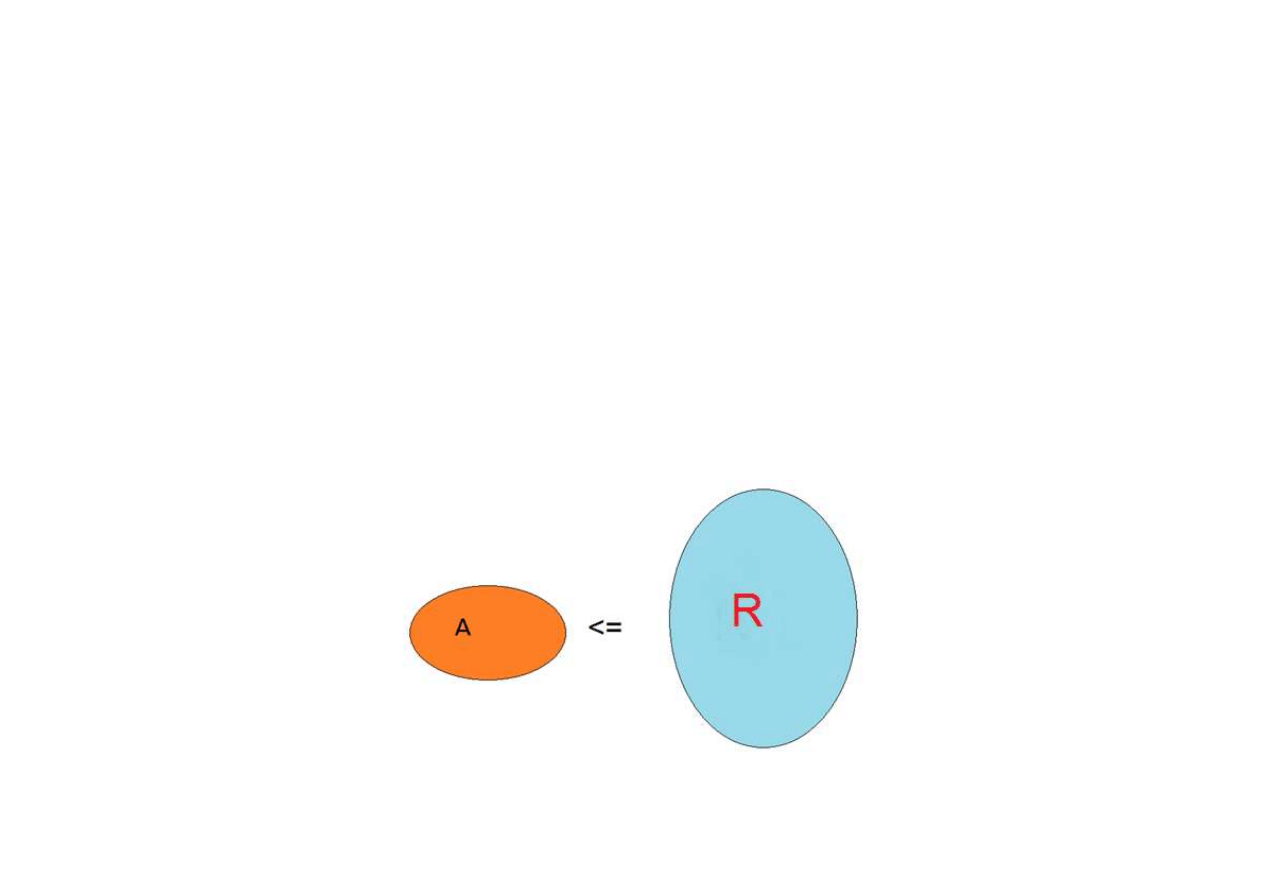
Problem wymiarowania konstrukcji sprowadza się do spełnienia
zależności:

A

≤

R

Gdzie:

A - obciążenia, wymuszenia

R – reakcja (nośność konstrukcji, sztywność)

.

W procesie historycznym w konstrukcjach metalowych wyodrębniły się

trzy podstawowe metody wymiarowania:

a) naprężeń dopuszczalnych,

b) naprężeń granicznych,

c) stanów granicznych.

Ad a) Najstarsza, sformułowana przez Navier (XVIII/XIX w.)

- Obciążenia - charakterystyczne

- naprężenia bezpieczne -

k (naprężenia dopuszczalne)

- naprężenia bezpieczne -

k (naprężenia dopuszczalne)

R

e

- normowa (charakterystyczna) granica plastyczności stali

n - arbitralnie przyjęty współczynnik bezpieczeństwa (n = 1,5

÷

1,7)

n

R

k

e

=

.

ad. b) Metoda naprężeń granicznych

Obciążenia - obliczeniowe

Pobl = P

⋅α

Naprężenia bezpieczne - K (naprężenia graniczne)

e

R

K

γ

=

Gdzie:

P - obciążenia normowe

α

- współczynnik bezpieczeństwa obciążenia (przeciążenia)

- współczynnik bezpieczeństwa materiału

γ

.

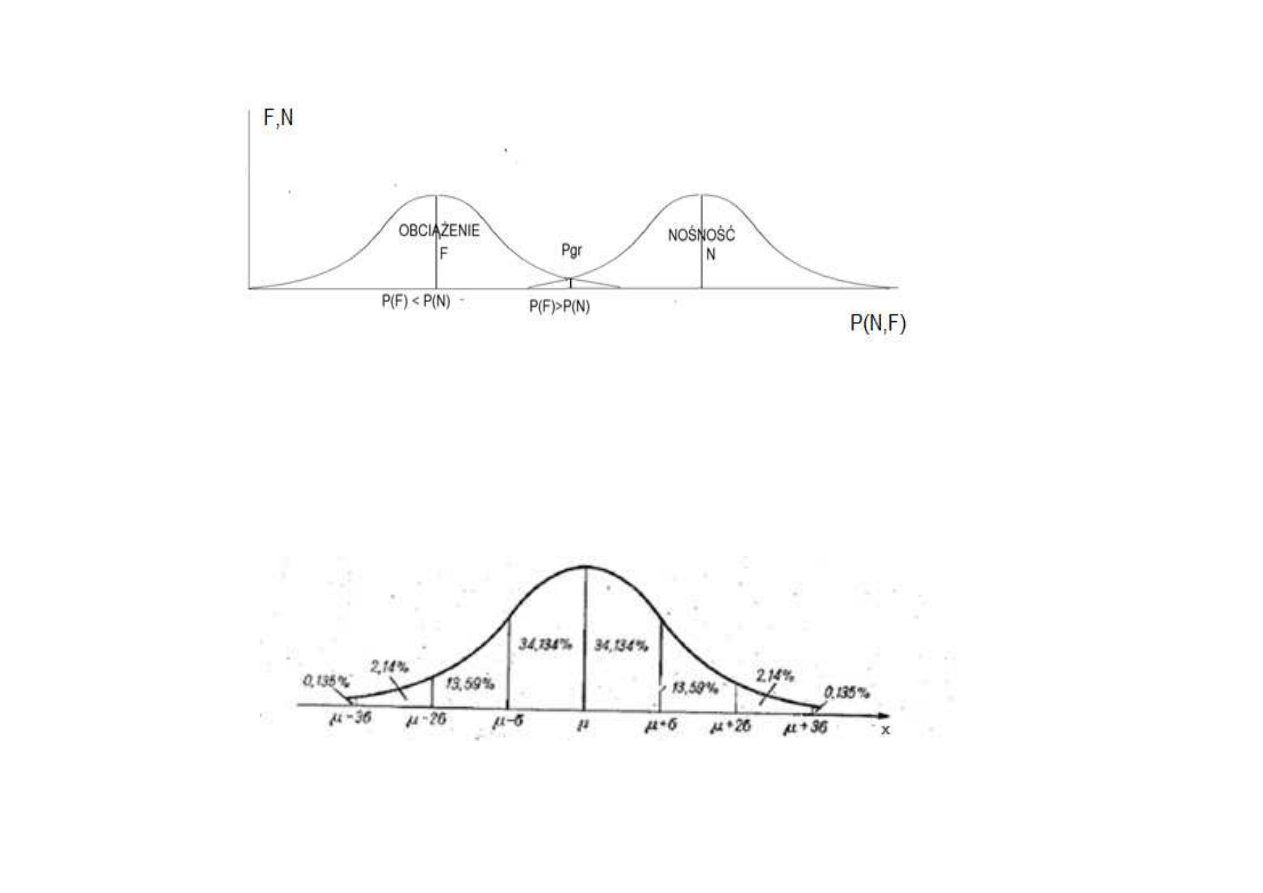
W metodzie stanów granicznych zakłada się, że obciążenie jak i
wytrzymałość konstrukcji mają charakter losowy. Obie zmienne

wytrzymałość konstrukcji mają charakter losowy. Obie zmienne
podlegają rozkładowi normalnemu.

.

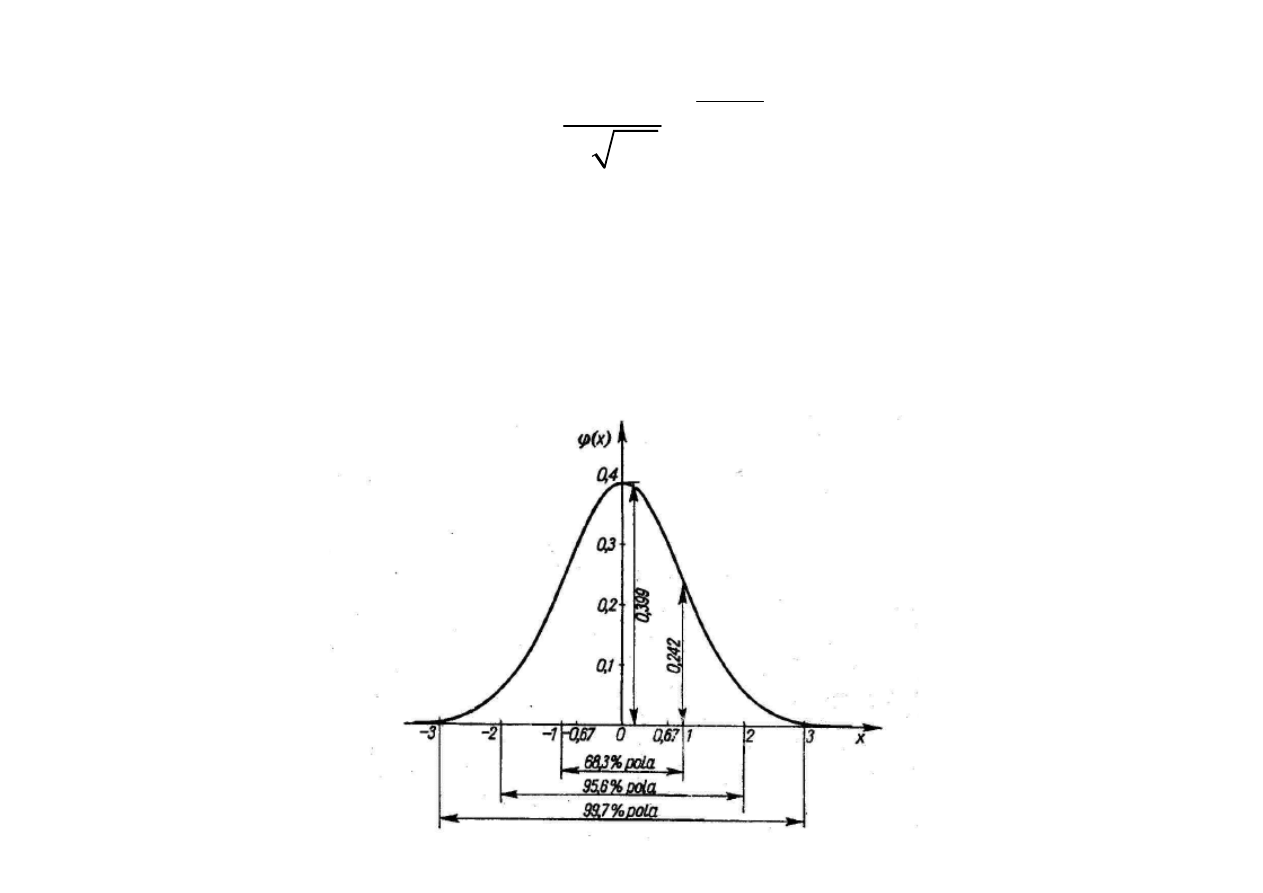
2

2

(

)

2

1

( )

2

x

x

e

µ

σ

ϕ

σ π

−

−

=

(

σ

> 0)

µ

- wartość przeciętna (wariancja)

( )

( )

E x

x

x dx

µ

ϕ

+∞

−∞

=

=

∫

σ

- odchylenie standardowe

2

( )

( )

D x

x

x dx

σ

ϕ

µ

+∞

−∞

=

= −

−

∫

.

Stąd wystarczająco bezpieczne jest przyjęcie granicy plastyczności Re

wg zasad:

To znaczy :

Stąd dla stali różnych granicach plastyczności wytrzymałości
obliczeniową określa się:

(

)

1 3

e

e

R

R

σ

=

−

(

)

0, 998

ei

e

p R

R

≤

=

obliczeniową określa się:

γ

s = 1,15

÷

1,25 dla Re = (355

÷

590)

s

e

d

R

f

γ

=

.

.

Norma PN-90/B-03200 przewiduje dwa stany graniczne, które należy

sprawdzić wymiarując konstrukcję.

- Stan graniczny nośności

Umowny stan wyczerpania nośności konstrukcji ze względu na

przekroczenie wytrzymałości, utraty stateczności lokalnej, utraty
stateczności ogólnej.

Konstrukcję, która została obciążona powyżej tego stanu uważamy za

niebezpieczny (przedawaryjny). W obliczeniach uwzględnia się

niebezpieczny (przedawaryjny). W obliczeniach uwzględnia się
obciążenia obliczeniowe.

- Stan graniczny użytkowania

Określa umowny stan, w którym konstrukcja traci swoje walory

użytkowe wskutek nadmiernych ugięć, przemieszczeń lub amplitudy
drgań oraz zmęczenia materiału.

W obliczeniach uwzględnia się obciążenia charakterystyczne.

.

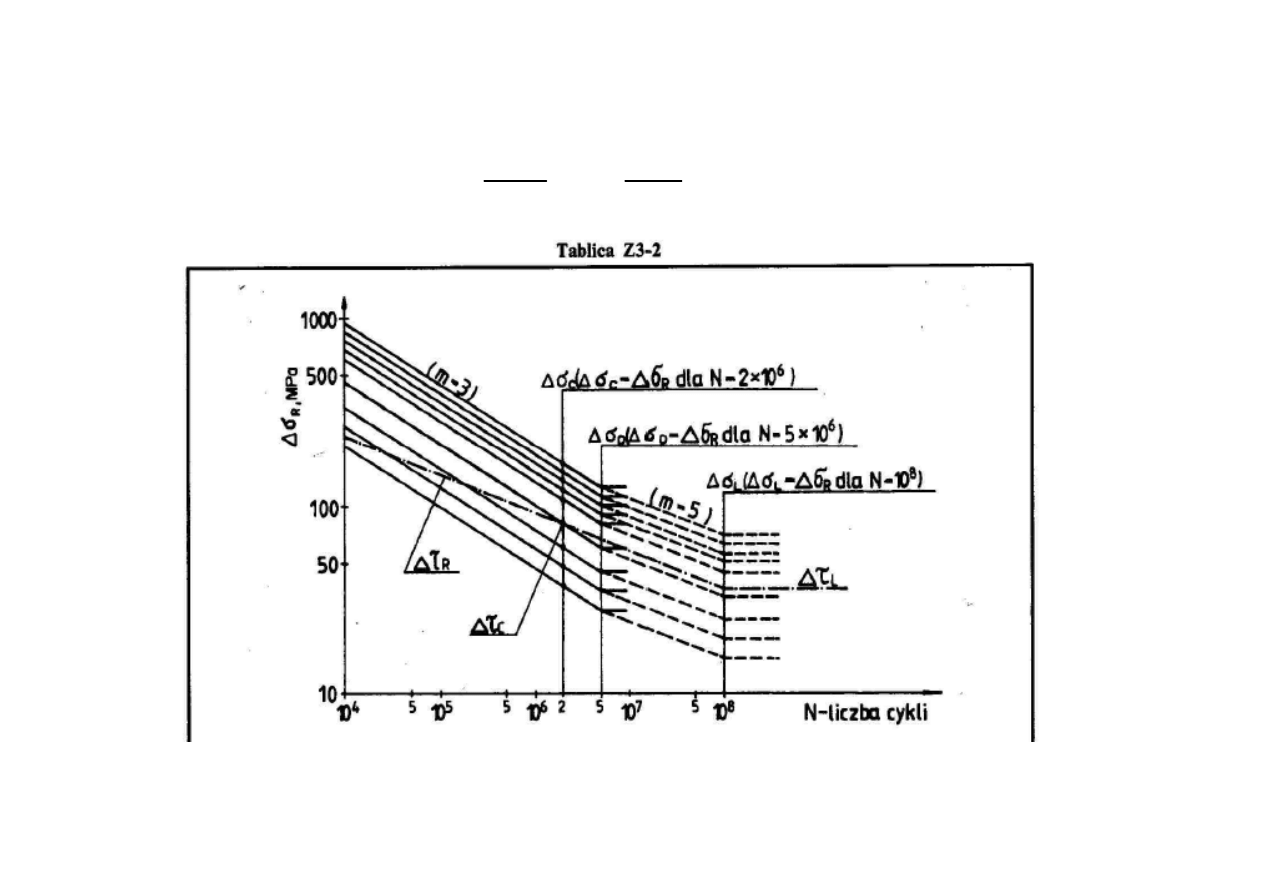
Wytrzymałość zmęczeniowa
Obliczenie elementów konstrukcji stalowych na zmęczenie należy

przeprowadzić dla konstrukcji poddanych obciążeniom wielokrotnie
zmiennym o liczbie cykli N > 1

⋅

10

4

.

W obliczeniach analizuje się zakres zmienności naprężeń (normalnych i

stycznych)

∆σ

=

σ

max

-

σ

min

∆τ

=

τ

max

-

τ

min]

W przypadku obciążeń naprzemiennych lub wyłącznie ściskających

(

∆σ

= 0) można przyjmować obliczeniowy zakres zmienności w postaci:

(

∆σ

t

= 0) można przyjmować obliczeniowy zakres zmienności w postaci:

∆σ

=

∆σ

t

+ 0,6

∆σ

e

Tak obliczony zakres zmienności naprężeń porównuje się z

wytrzymałością zmęczeniową

∆σ

R

,

∆τ

R

∆σ ≤ ∆σ

R

/

γ

fnt

(

γ

fnt

- wyjściowy wsp. bezpiecz.)

∆τ ≤ ∆τ

R

/

γ

fnt

(

γ

fnt

= 1

÷

1,2)

.

0

,

1

2

R

e

2

R

e

≤













τ

∆

τ

∆

+













σ

∆

σ

∆

Stan graniczny użytkowania f fgr

≤

.

Przemieszczenia poziome konstrukcji:

a)

w układach jednokondygnacyjnych (bez suwnic)

przy obudowie wrażliwej na pękanie

h/250

w pozostałych przypadkach

h/150

b)

w układach wielokondygnacyjnych

h

i

/500

Drgania

Częstotliwość drgań stropu w budynkach użyteczności publicznej,
gdy

l > 12,0m n < 5Hz.

Warunku można nie sprawdzać, gdy ugięcie konstrukcji od
kombinacji obciążeń długotrwałych f < 10 mm.

.

Obciążenia
Obciążenia obliczeniowe

P =

γ

f

⋅

P

k

gdzie:

γ

f

- współczynnik obciążenia

P

k

- obciążenie obliczeniowe na podstawie norm lub arbitralnie

przyjęte przez projektanta

Ponadto w normie obciążeń występuje tzw. współczynnik konsekwencji

Ponadto w normie obciążeń występuje tzw. współczynnik konsekwencji

zniszczenia

γ

n

γ

n

= 1,0 dla typowych warunków

W specyficznych przypadkach projektant może przyjąć

γ

n

> 1,0 lub

γ

n

< 1,0

,

w zależności od spodziewanych ekonomicznych i społecznych skutków

zniszczenia.

P =

γ

n

⋅γ

f

⋅

P

k

.

Przegląd norm obciążeń
PN-80/B-02000 "Obciążenia budowli. Zasady ustalania wartości„
( PN-EN 1990 i PN-EN-1991-1)

Obciążenia dzieli się na:

obciążenia stałe - obciążenia, którego wartość, kierunek i położenie
pozostają niezmienne w czasie użytkowania budowli lub w innym
rozpatrywanym okresie (np. czas montażu lub remontu),
obciążenie zmienne - obciążenie, którego wartość, kierunek i
położenie mogą zmieniać się w czasie użytkowania budowli lub w
innym rozpatrywanym okresie

Rozróżnia się:

Rozróżnia się:

obciążenie zmienne w całości długotrwałe:

a) ciężar własny konstrukcji,
b) ciężar własny urządzeń związanych z konstrukcją,
c) ciężar własny i parcie ciał sypkich i gazów wypełniających stale

urządzenia (np. ciśnienie powietrza w przewodach wentylacyjnych),

d) obciążenie gruntem budowli zagłębionych w gruncie,
e) parcie wody o stałym poziomie zwierciadła,
f) obciążenie temperatury w procesie eksploatacji urządzeń stałych,

.

obciążenia zmienne w całości krótkotrwałe

a) obciążenia w czasie wykonywania, transportu i wznoszenia

konstrukcji, montażu urządzeń i tymczasowego składania
materiałów,

b) obciążenia spowodowane rozruchem urządzeń i zatrzymywaniem w

wer. przejściowych i badawczych,

c) obciążenie atmosferyczne:

śniegiem, wiatrem, oblodzenia, krą

wyjątkowe

wyjątkowe

a) uderzenie pojazdami,

b) obciążenia sejsmiczne,

c) obciążenia spowodowane wybuchem,

d) działanie pożaru,

e) awaria urządzeń,

i) obciążenie spowodowane powodzią,

j) huraganowym wiatrem.

.

Kombinacje obciążeń

W stanie granicznym nośności:

podstawowe:

wyjątkowe:

W stanie granicznym użytkowania:

∑

∑

γ

Ψ

+

⋅

γ

m

1

n

1

K

f

o

TK

f

i

i

i

i

i

Q

C

∑

∑

+

γ

+

⋅

γ

n

1

n

1

a

K

f

TK

f

F

Q

8

,

0

C

i

i

i

i

m

∑

- obciążenie charakterystyczne stałe,

- obciążenie charakterystyczne zmienne

F

a

- obciążenie charakterystyczne wyjątkowe,

ψ

o

- współczynnik jednoczesności obciążeń zmiennych

1

i

m

TK

K

G

Q

+

∑

- najniekorzystniejszy ...

TKi

G

K

Q

.

PN-82/B-02001 Obciążenie budowli. Obciążenie stałe

γ

= 1,1

÷

1,3 lub

γ

= 0,9

Lp.

Znaczenie obciążeń

ψ

o

1
2
3
4

Podstawowe
Drugie
Trzecie
Wszystkie pozostałe

1,0
0,9
0,8
0,7

γ

f

= 1,1

÷

1,3 lub

γ

f

= 0,9

PN-82/B-02003 Obciążenie budowli. Obciążenie zmienne i

technologiczne. podstawowe obciążenie technologiczne i
montażowe.

.

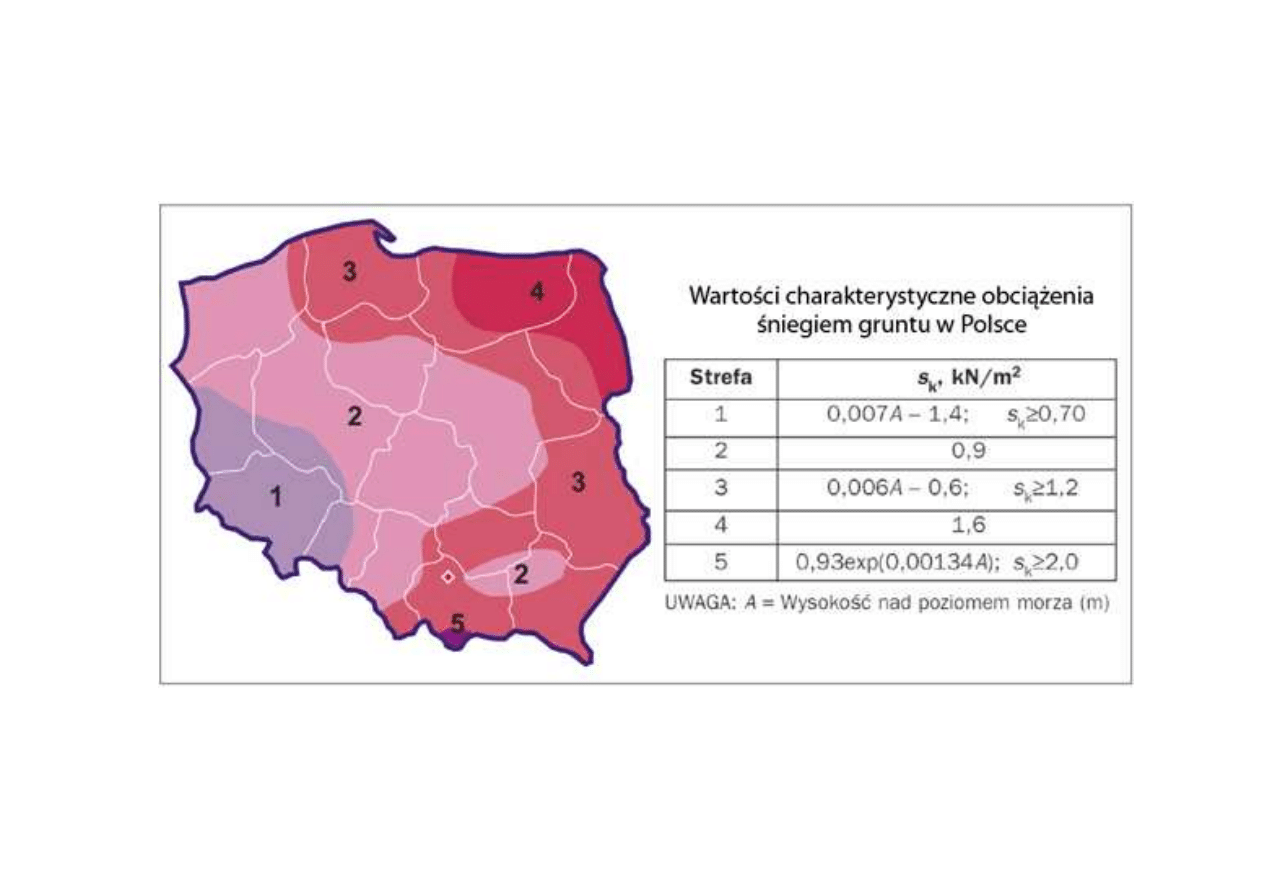
Obciążenie śniegiem PN-80/B 02010/Az1-2006 (PN-EN-1991-1-3)

Wartości obliczeniowe obciążenia śniegiem

S = S

k

⋅

C

⋅γ

f

Gdzie:

S

k

- charakterystyczne obciążenie sniegiem na poziomie gruntu

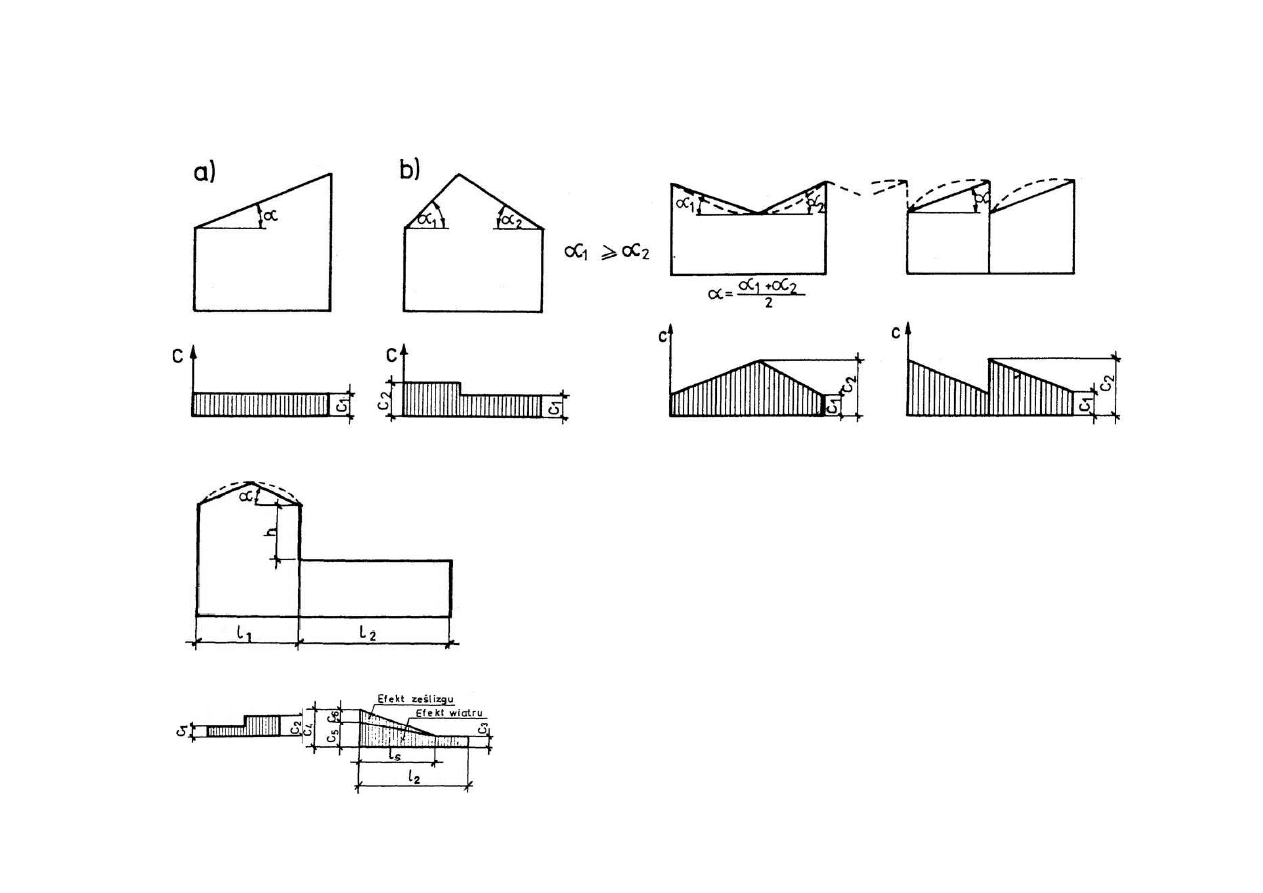
C- współczynnik kształtu dachu ( C=0,8 do 2,5)

γγ

f

= 1,5 obliczeniowy współczynnik bezpieczeństwa

.

.

Dla dachów należy uwzględniać możliwość koncentracji śniegu ( worki śnieżne)

.

Obciążenie wiatrem.PN-77/B-02011/Az1:2009 (PN-EN-1991-4:2008AC).

Obciążenie wiatrem skierowane jest prostopadle do przegrody

Obciążenie charakterystyczne

p

k

= q

k

⋅

C

e

⋅

C

⋅β

Gdzie

V - charakterystyczna prędkość wiatru. Średnia 10 minutowa mierzona

2

V

q

2

k

k

⋅

ρ

=

V

k

- charakterystyczna prędkość wiatru. Średnia 10 minutowa mierzona

na wysokości 10m nad poziomem gruntu w terenie otwartym, która
może być przekroczona średnio 1 raz w przewidywanym okresie
użytkowania budowli - 50 lat (dla 80% V

k

= 20m/s)

ρ

= 1,23kg/m

2

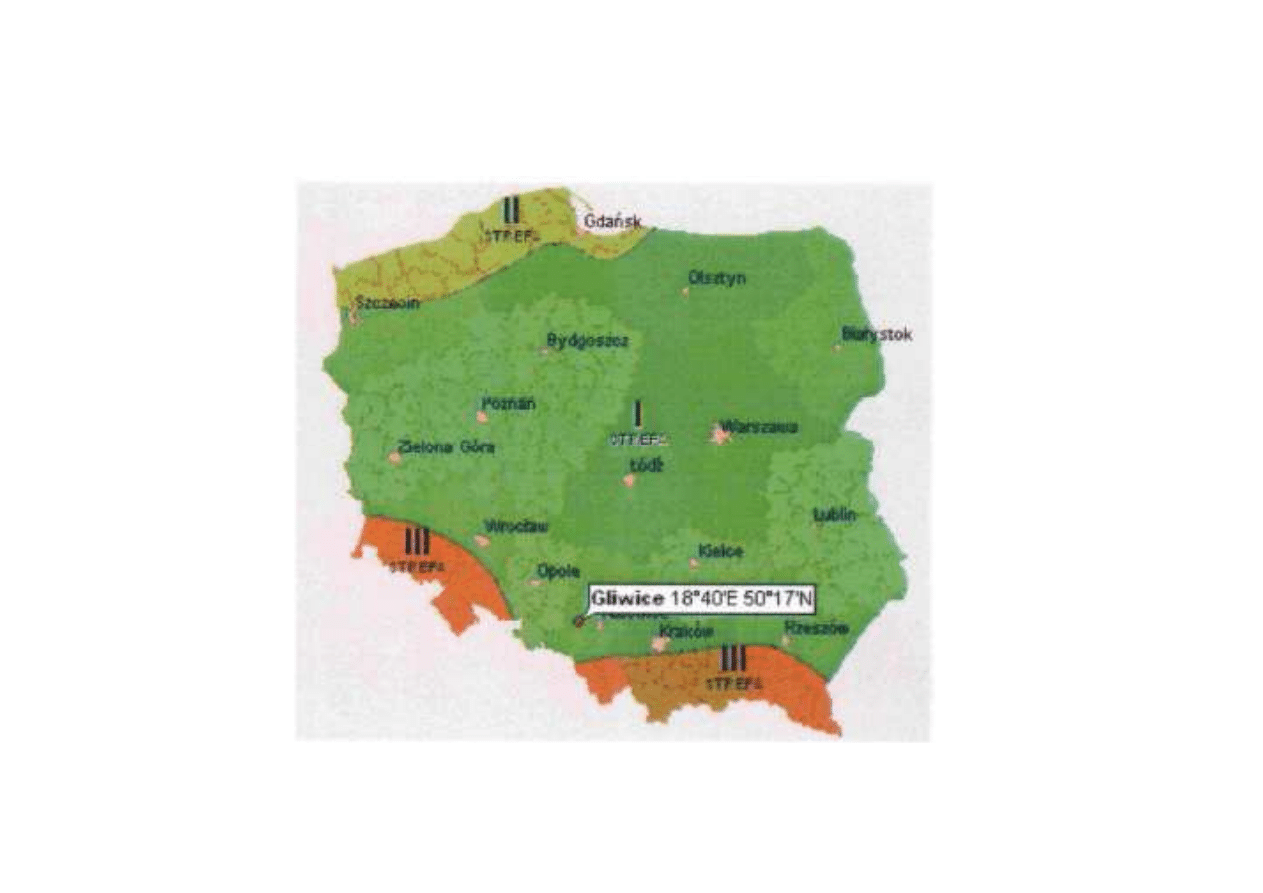
Wartość q

k

- zależy od strefy obciążenia

.

.

C

e

- współczynnik ekspozycji - zależy od rodzaju terenu:

A - otwarty z nielicznymi przeszkodami,

B - zabudowany przy wysokości istniejących budynków do 10 m (....) lub

zalesiony

C - zabudowany przy wysokości budynków pow. 10 m

C

e

≥

1,0 tablica 4, rysunek 3 normy

C - współczynnik aerodynamiczny zależy od kształtu powierzchni

dziłania, kąta nachylenia do kierunku wiatru

dziłania, kąta nachylenia do kierunku wiatru

C=-0,3 do 2,0 ( - ssanie, + parcie)

β

- współczynnik dynamiczny - zależy od okresu drgań własnych i

dekrementu tłumienia

∆

dla konstrukcji niepodatnych (większość budynków)

β

= 1,8

Obciążenie obliczeniowe wiatru:
p = p

k

⋅γ

f

;

γ

f

= 1,5

.

Wg. EC3

Nośność obliczeniowa

gdzie :

R

k

- wartość charakterystyczna nośności określona na podstawie cech

materiału

- współczynnik materiałowy

k

d

m

R

R

γ

=

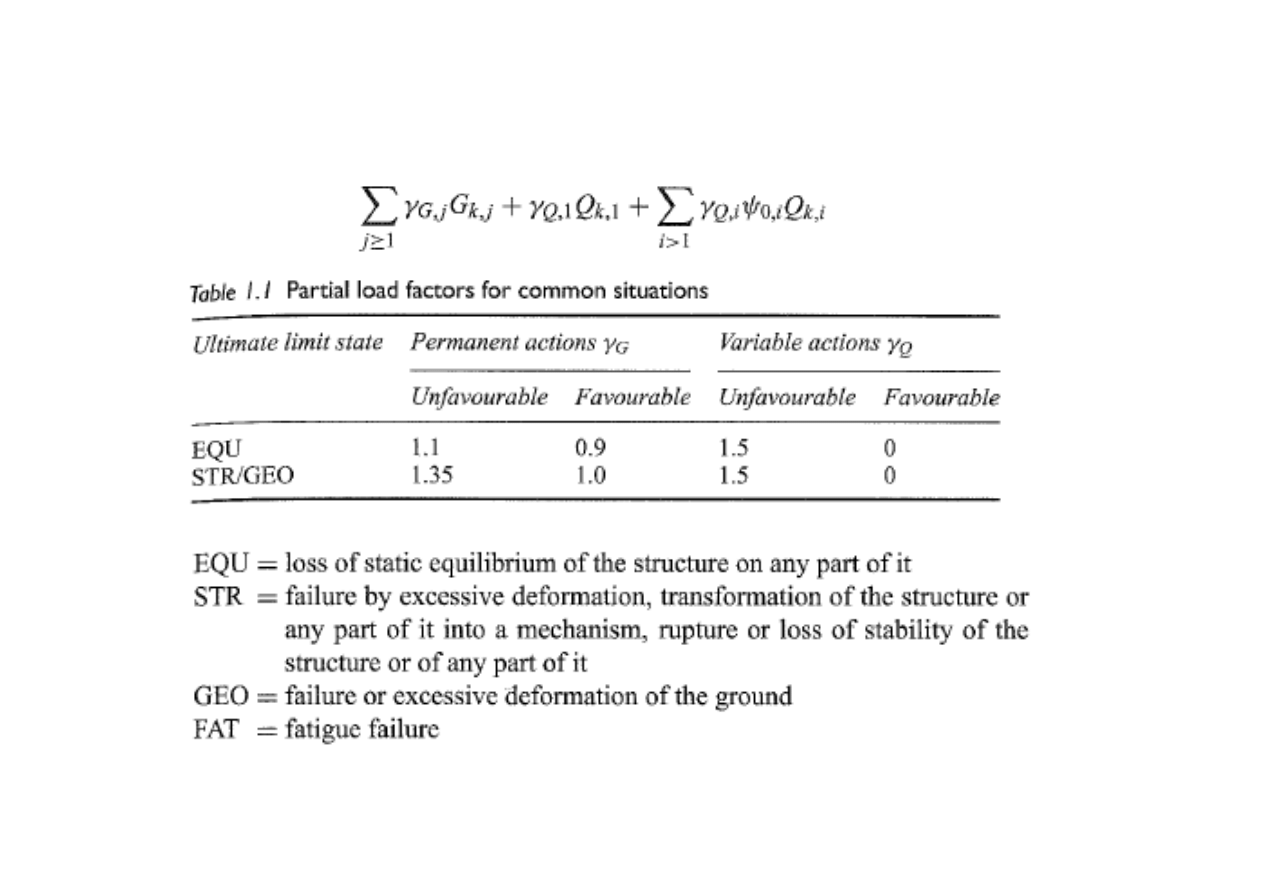
M

γ

W przypadku budynków przyjmuje się następująco:

.

Obciążenia i kombinacja obciążeń;

.

•

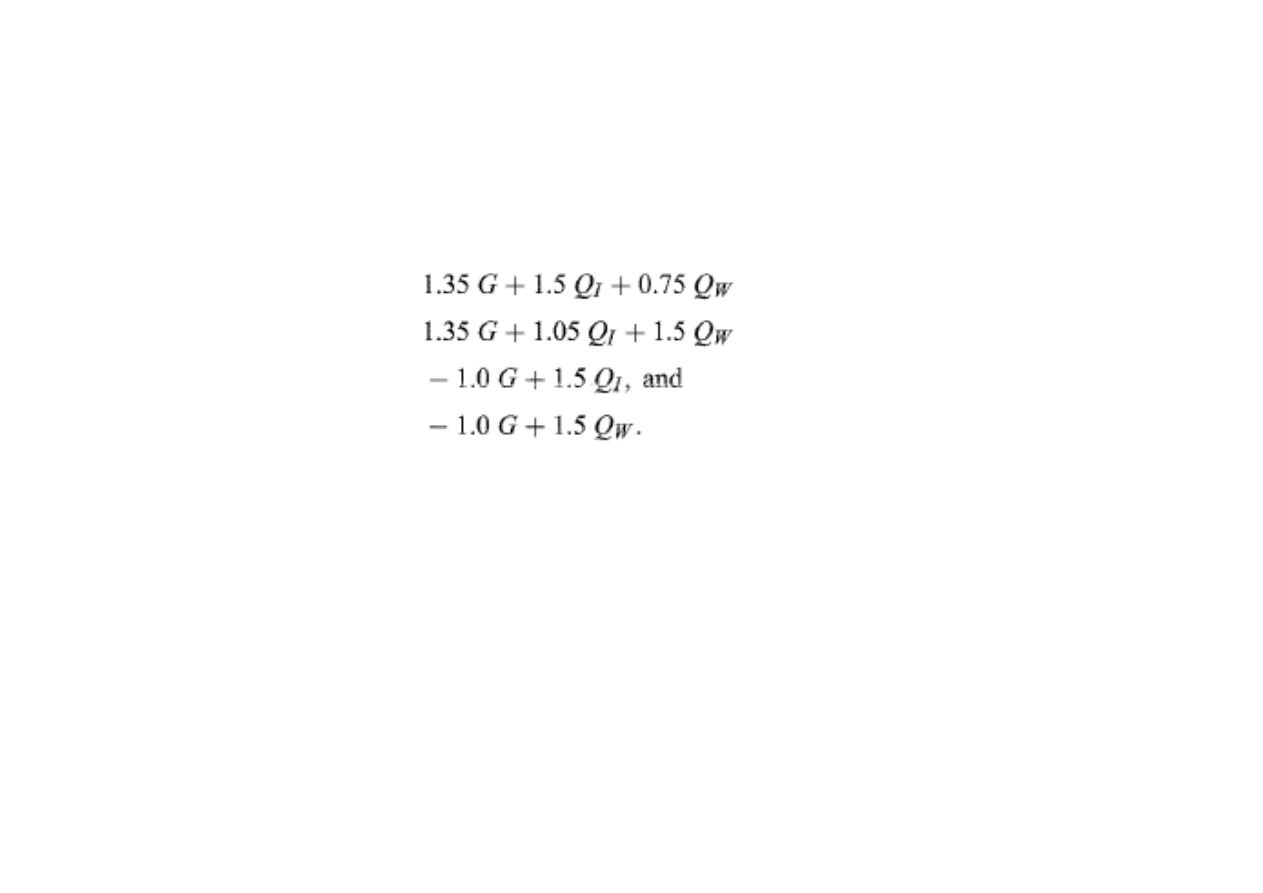
W przypadku budowli obciążonej ciężarem własnym G, obciążeniem
użytkowym Q

l

i obciążeniem wiatrem Q

w

kombinacje dla będą

następujące:

.

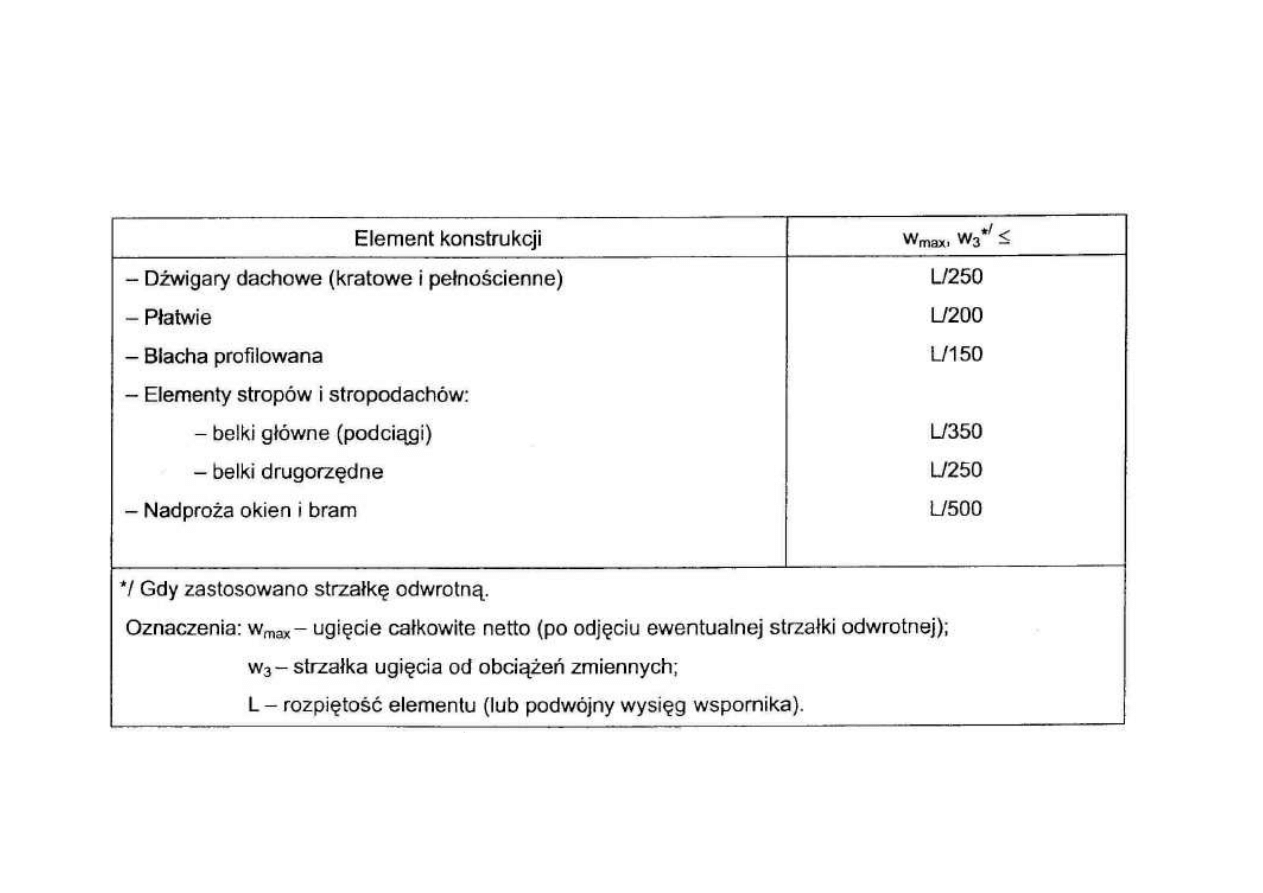
Graniczne ugięcia wynoszą: