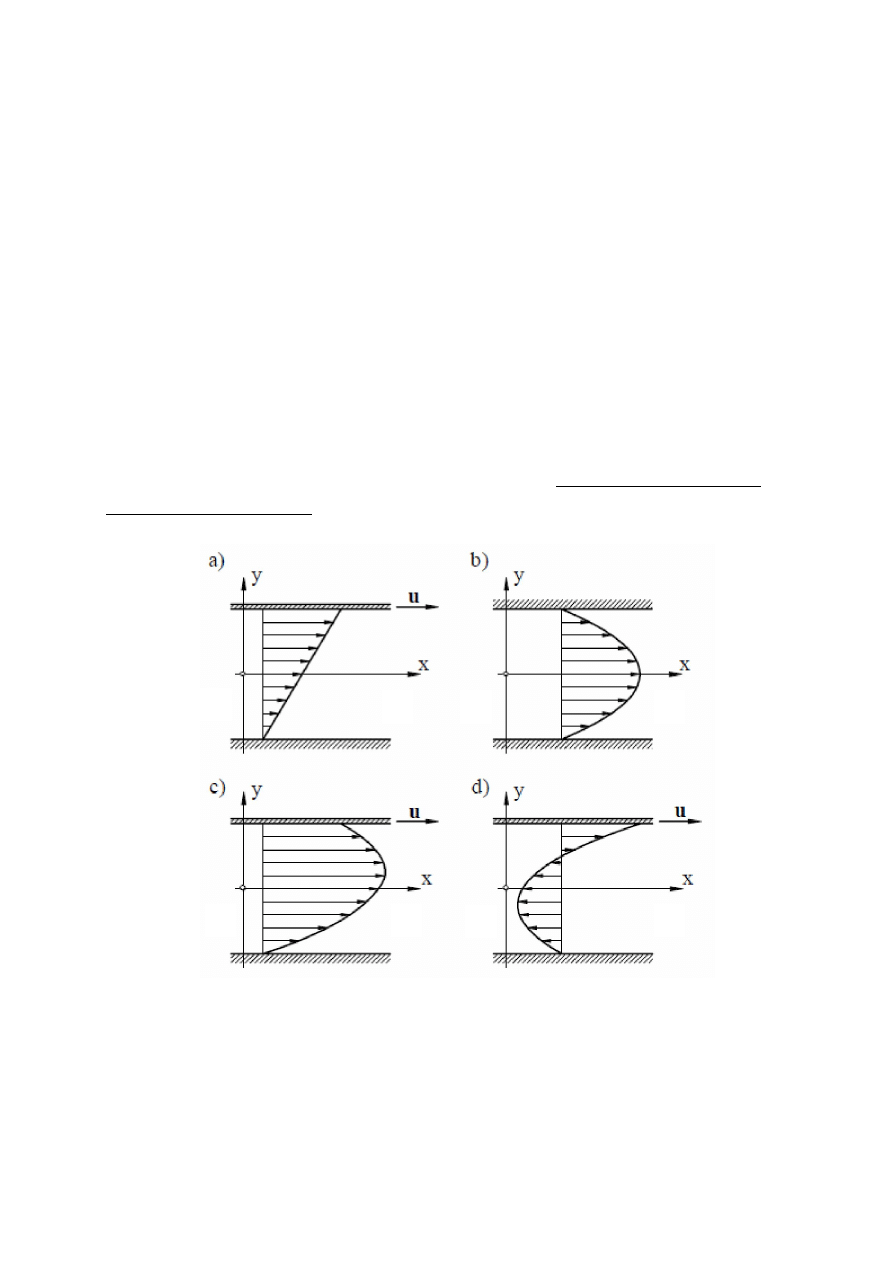
1

RODZAJE RUCHU PŁYNU RZECZYWISTEGO

PRZEPŁYW LAMINARNY

Ruch płynu odbywa się tak jakby poszczególne warstwy ślizgały się po

sobie (stąd nazwa przepływ uwarstwiony) bez wymiany pędu i masy między
warstwami.
Można to zaobserwować wprowadzając do przepływu zabarwioną cienką strugę
barwnika. Struga barwnika pozostaje wyraźna na długiej drodze.

W rzeczywistości występuje wymiana masy i pędu w skali

mikroskopowej co jest przyczyną występowania naprężeń stycznych.

Chwilowe zaburzenia w ruchu są tłumione ponieważ siły lepkości przeważają
nad siłami bezwładności.

Profile prędkości w laminarnym przepływie między płaskimi ścianami:

a) Δp =p

1

-p

2

= 0, u > 0,

przepływ laminarny Couette’a

b) Δp > 0, u = 0,

przepływ laminarny Poiseuille’a

c) Δp > 0, u > 0,

d) Δp < 0, u > 0

p

1

p

2

p

1

p

2

p

1

p

2

p

1

p

2

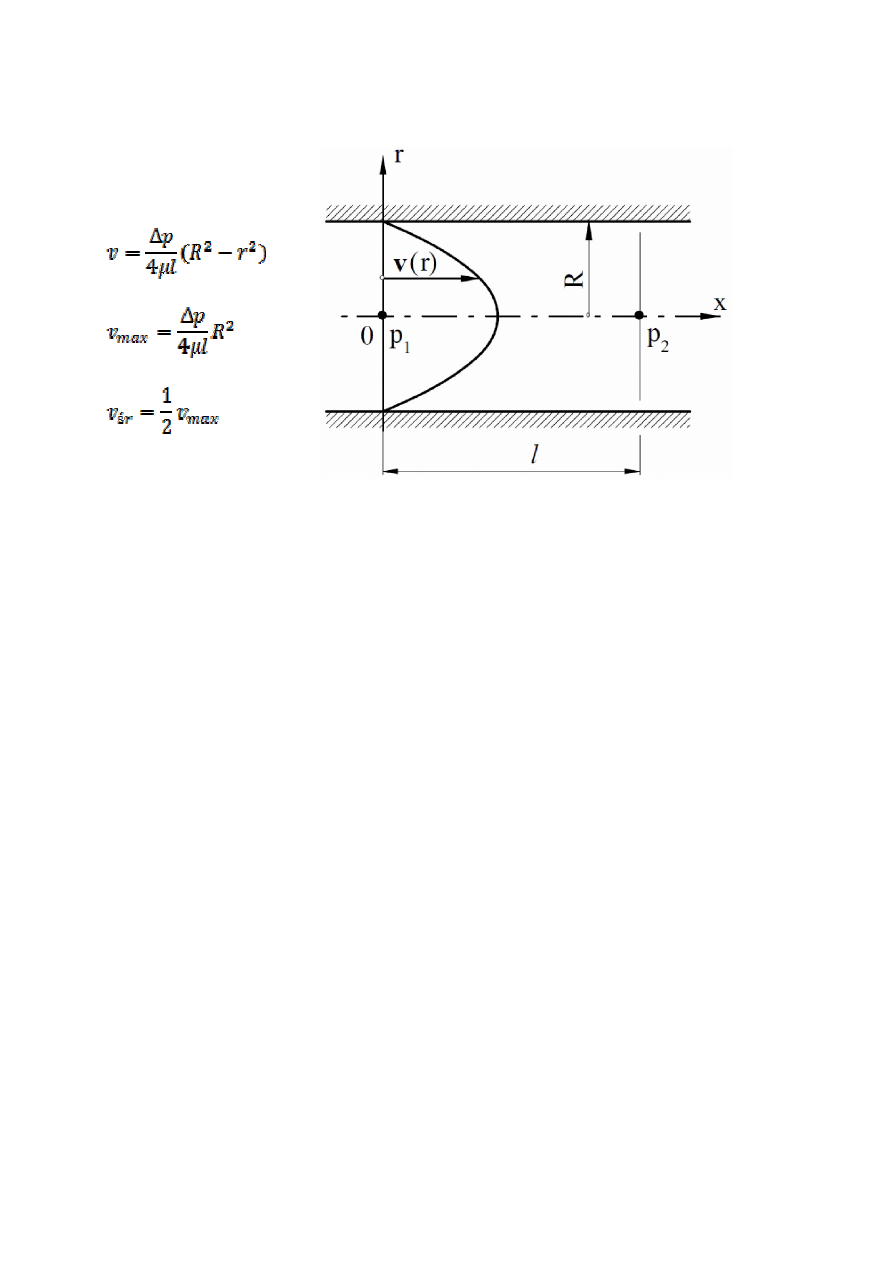
2

Rozkład prędkości w osiowo-symetrycznym przepływie laminarnym Hagena–

Poiseuille’a

3

PRZEPŁYW TURBULENTNY

- chaotyczny i nieregularny ruch elementów płynu,
- duża intensywność procesów transportu masy i pędu w skali makroskopowej,
- wszystkie wielkości, charakteryzujące dany przepływ, wykazują zmienność
zarówno w czasie, jak i w przestrzeni.

W ruchu turbulentnym siły bezwładności przeważają nad siłami lepkości i

tłumiące działanie lepkości jest niewystarczające dla utrzymania stateczności
ruchu laminarnego.

Turbulencja - zjawisko charakteryzujące się występowaniem w
przepływającym płynie chaotycznych fluktuacji parametrów hydro- i
termodynamicznych (prędkości przepływu, ciśnienia, gęstości, temperatury).
Występują wiry o bardzo zróżnicowanej skali i energii.

Hipoteza Reynoldsa - przepływ turbulentny może być przedstawiony jako
superpozycja przepływu uśrednionego i fluktuacyjnego.

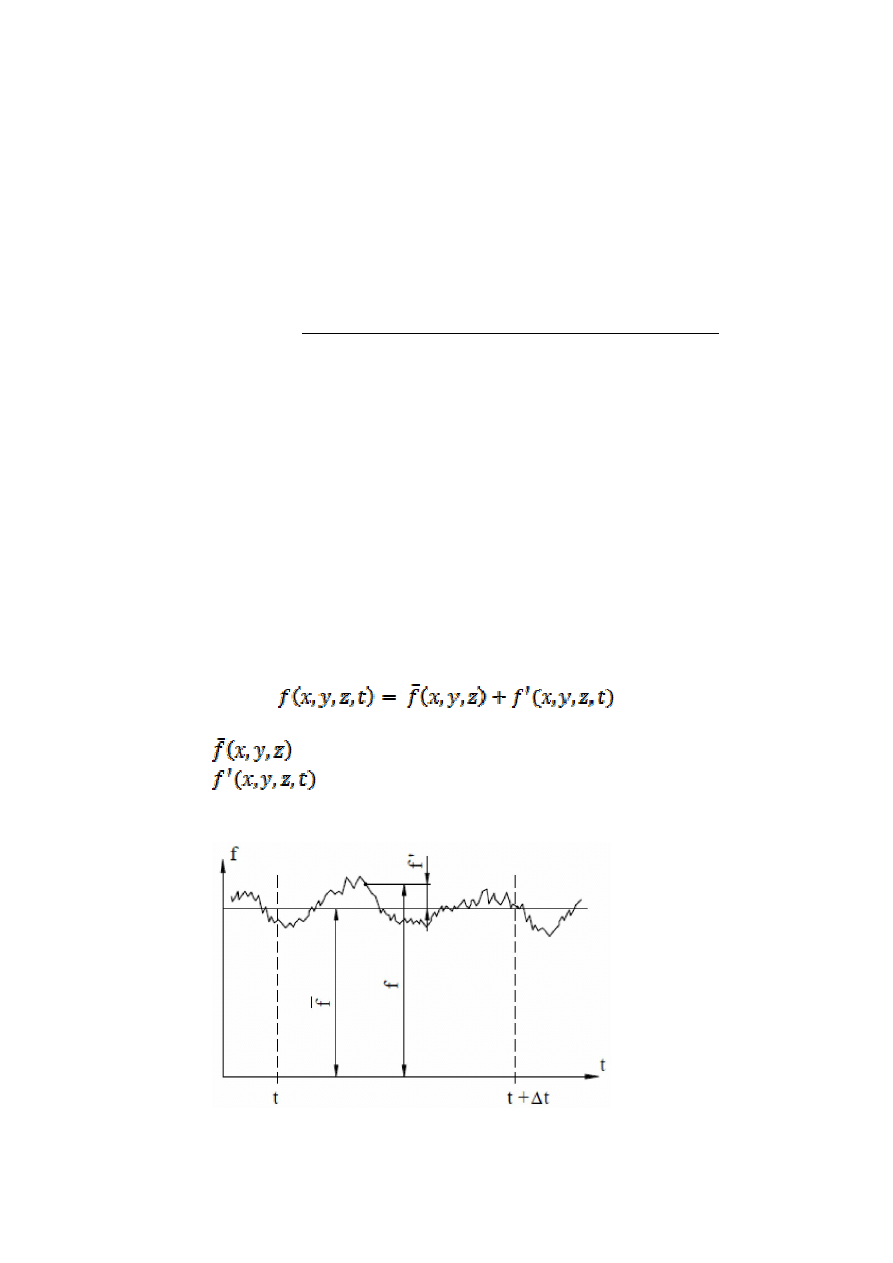
Dowolny parametr f (x, y, z, t) ruchu turbulentnego można przedstawić w postaci
sumy

gdzie:

- wartość uśredniona funkcji f,

- fluktuacja będąca wielkością małą i szybkozmienną

w porównaniu z f

Przebieg wielkości f czasie w tym samym punkcie przestrzeni

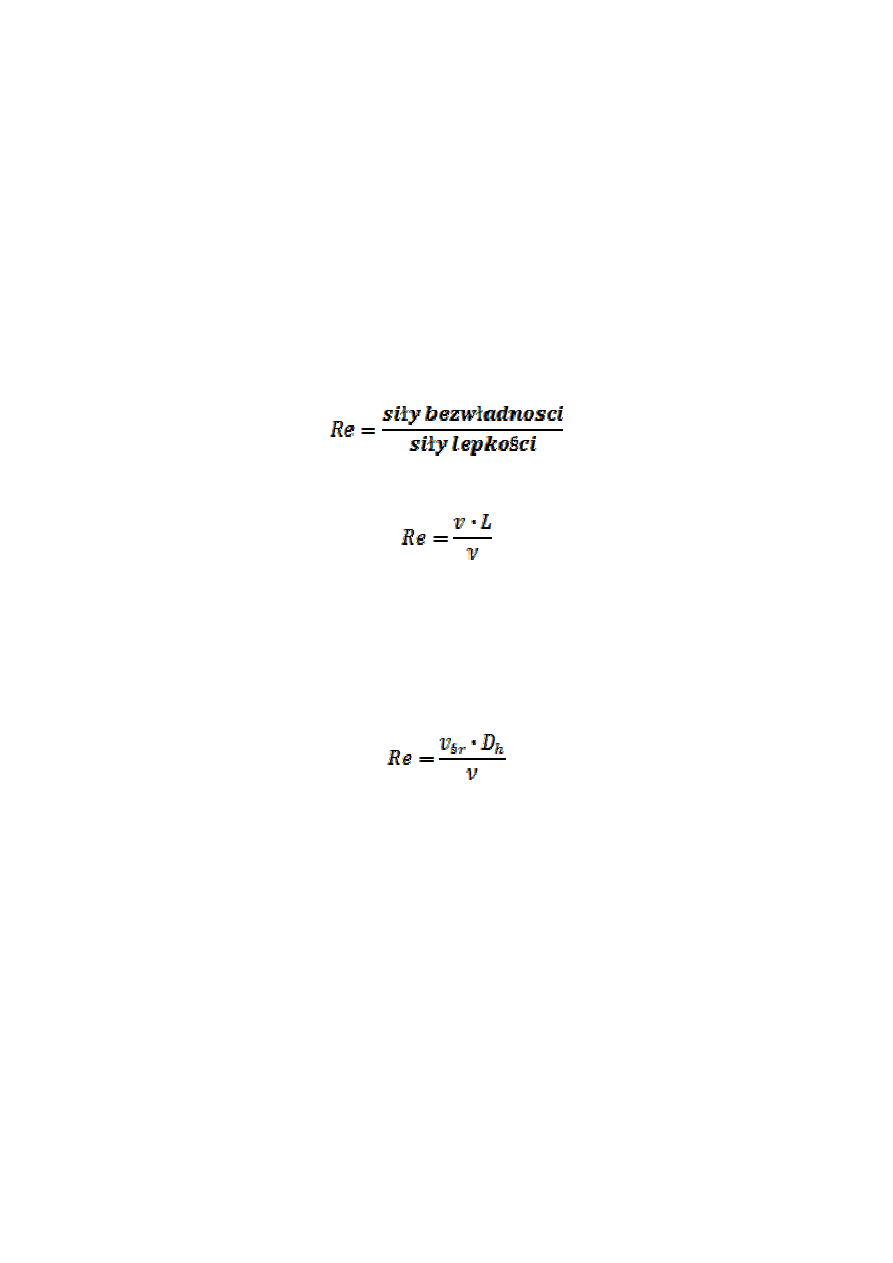
4

Przy takim założeniu rozpatrujemy pole wielkości średnich czasowych.

Ustalony ruch turbulentny – ruch, w którym prędkość uśredniona jest stała.

W ruchu turbulentnym występują znaczne naprężenia styczne co ma wpływ na
rozkład prędkości w przekroju przepływowym oraz zwiększenie oporów ruchu.


LICZBA REYNOLDSA

Liczba kryterialna określająca charakter przepływu.

Analiza wymiarowa sił prowadzi do wzoru

Gdzie :

v –prędkość charakterystyczna dla danego przepływu,

L –wymiar liniowy charakterystyczny dla tego przepływu,

ν – lepkość kinematyczne płynu

Dla przepływu przez kanały przyjmuje się:

v

śr

– średnia prędkość w kanale (uśredniona ze strumienia objętości),

D

h

– średnica hydrauliczna kanału,

D

h

=4A/U

A – pole przekroju,

U - obwód zwilżony w danym przekroju.

Dla przewodu o przekroju kołowym (rura) D

h

– d (średnica rury)

Krytyczna liczba Reynoldsa – wartość liczby Re przy której następuje zmiana
charakteru przepływu

Dla przekroju kołowego i warunków technicznych przyjmuje się

Re

kr

≈2300

5

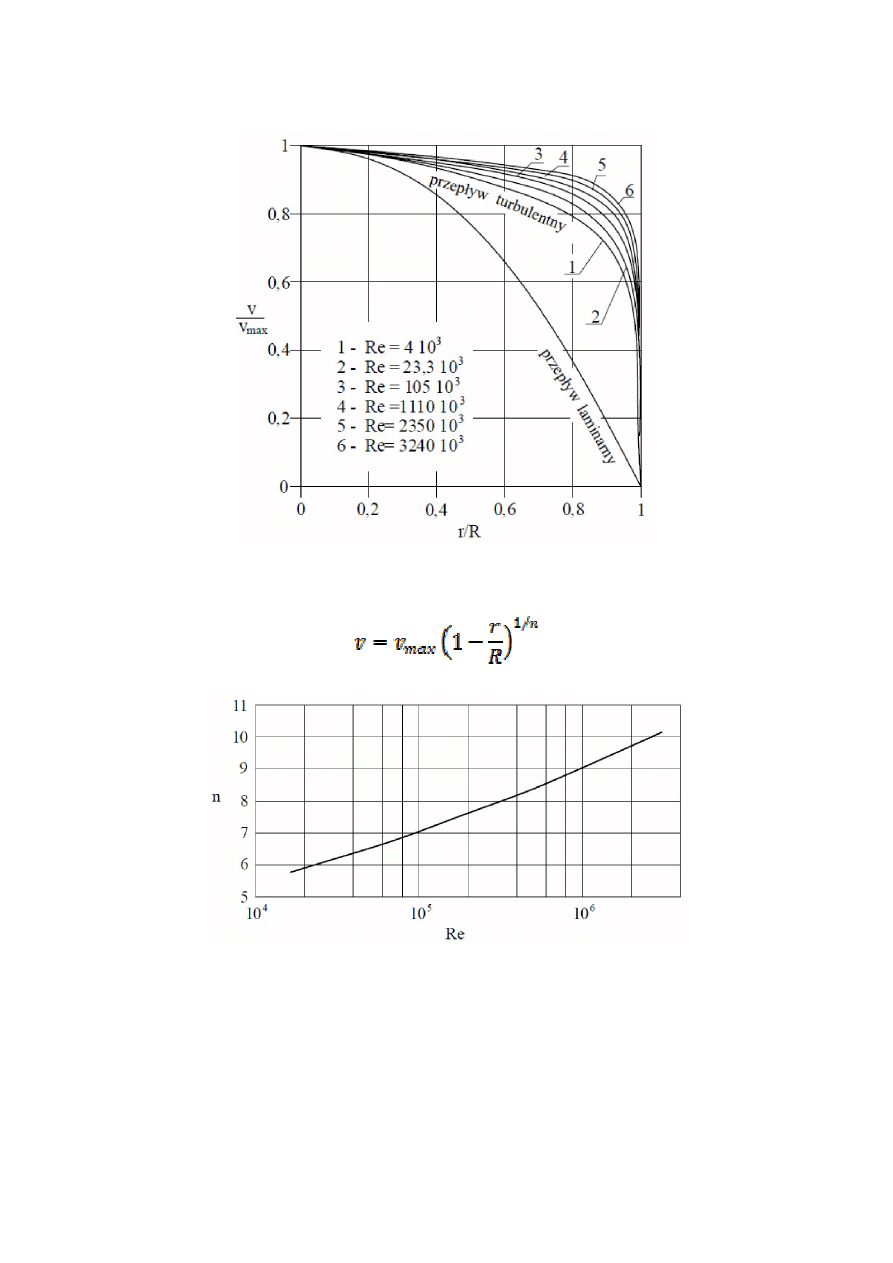
Rozkład prędkości w gładkim przewodzie przy różnych liczbach Reynoldsa

Zależność

n od liczby Reynoldsa

6

WARSTWA PRZYŚCIENNA

W przepływach występujących w warunkach technicznych najczęściej

przeważają siły bezwładności nad siłami lepkości (woda, powietrze itp.).

Siły lepkości odgrywają istotną rolę jedynie w pobliżu ścianek

ograniczających przepływ. Ten obszar nazywa się warstwą przyścienną.

Poza rejonem warstwy przyściennej siły lepkości są tak małe w

porównaniu z siłami bezwładności, że można traktować ciecz jak doskonałą
(tzw. pseudodoskonałą).

Ciśnienie w warstwie przyściennej jest stałe wzdłuż normalnej do opływanej
powierzchni. Ta właściwość jest wykorzystywana przy pomiarze ciśnienia
statycznego w przekroju kanału. Wystarczy zmierzyć ciśnienie w otworku
wykonanym w ścianie kanału.

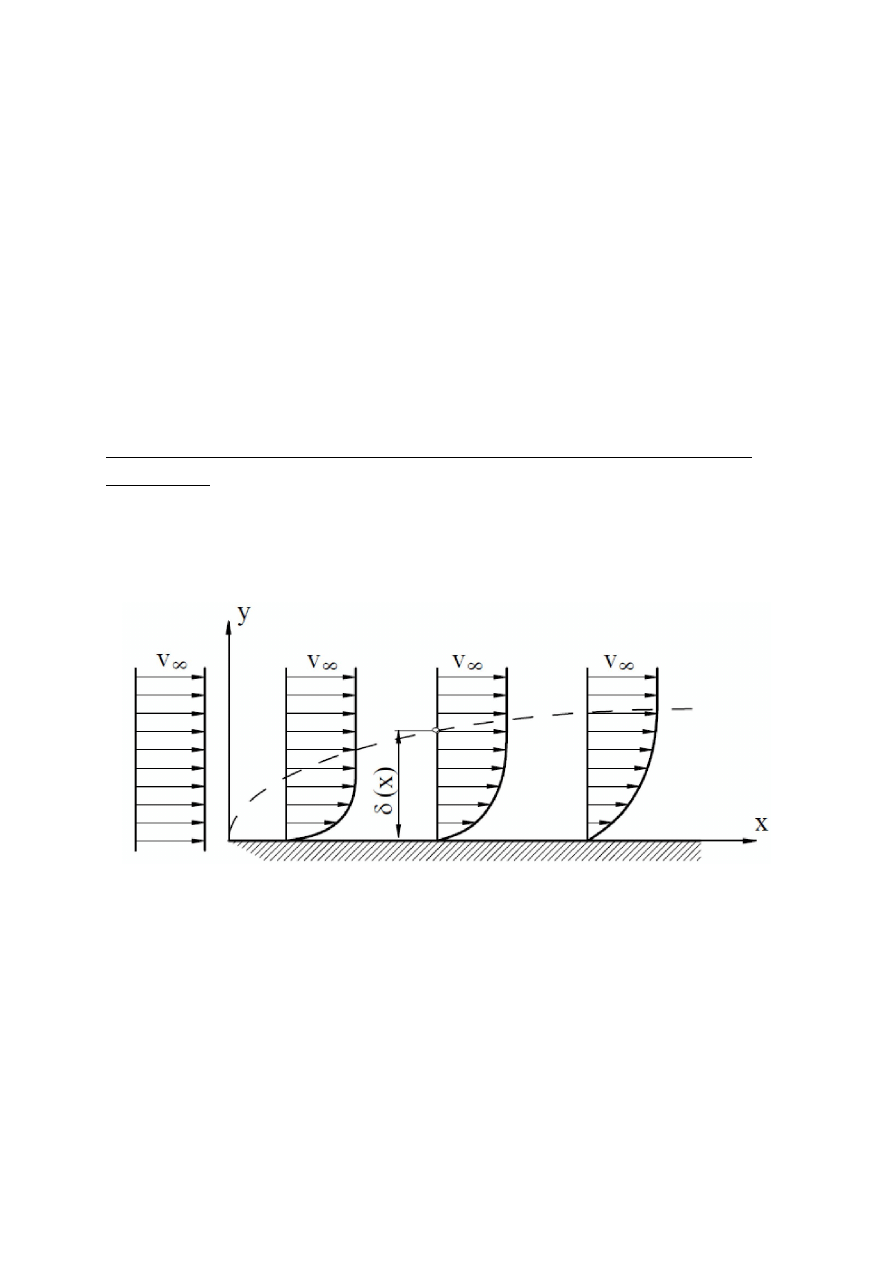
Obraz warstwy przyściennej na płaskiej ściance

7

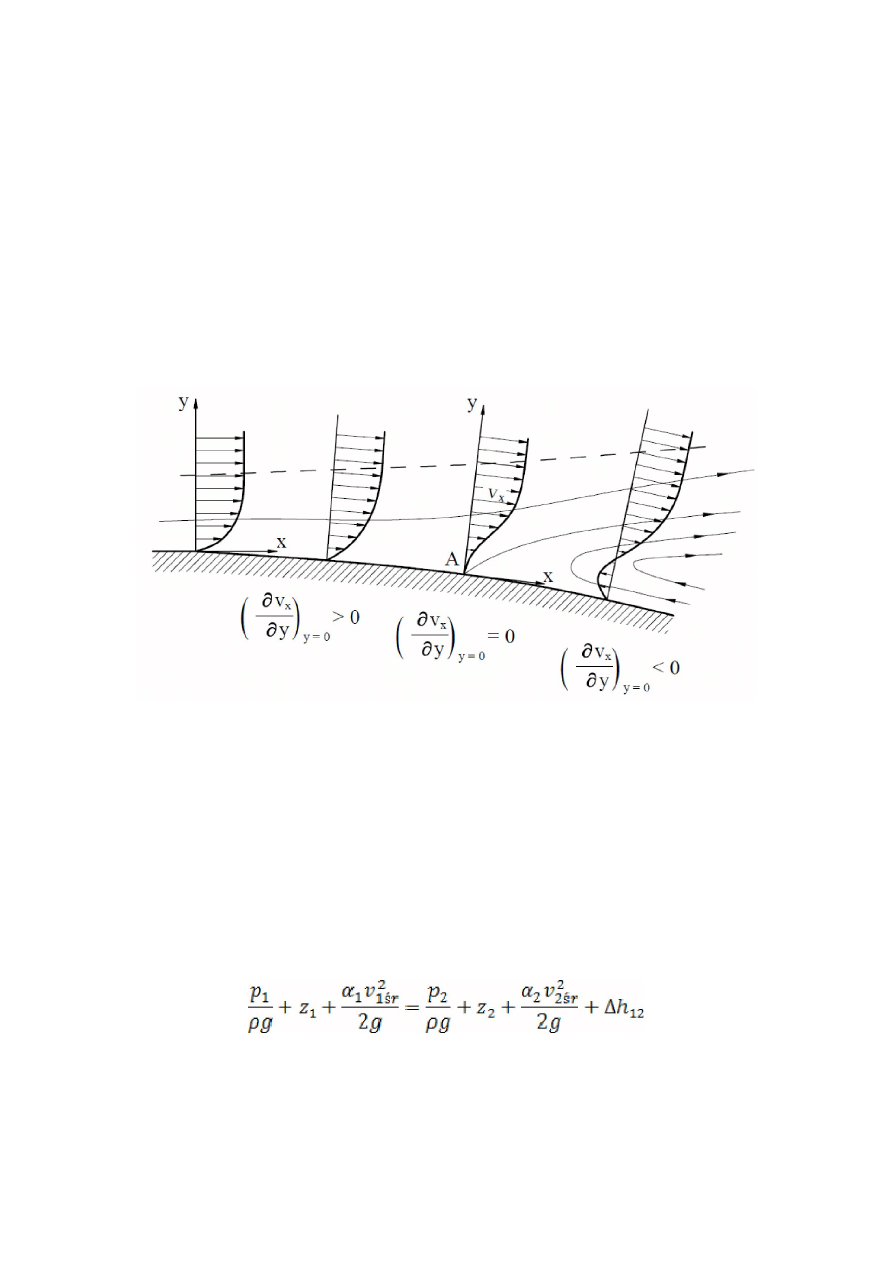
Oderwanie warstwy przyściennej występuje gdy przepływ odbywa się w

kierunku wzrostu ciśnienia (∂p/∂x> 0

)

. Zbyt mała energia kinetyczna płynu w

pobliżu ścianki nie wystarcza na pokonanie siły ciśnienia i następuje odwrócenie
kierunku przepływu.

Zjawisko oderwania zależy od charakteru ruchu w warstwie przyściennej.

W ruchu turbulentnym, w wyniku intensywnej wymiany elementów płynu,
warstwa przyścienna jest zasilana w energię kinetyczną i dlatego w tym
przypadku zjawisko oderwania następuje później.

Dla przepływów z ujemnym gradientem ciśnienia ∂ p/∂ x < 0, (konfuzory)

kiedy prędkości wzrastają oderwanie warstwy przyściennej nie występuje.

Oderwanie warstwy przyściennej

UOGÓLNIONE RÓWNANIE BERNOULLIEGO

Jest to równanie Bernoulliego uwzględniające fakt, że w przeływie płynu
lepkiego część energii mechanicznej zostaje zamieniona na ciepło w wyniku sił
tarcia (poniżej zapisane w jednostkach wysokości).

W równaniu operujemy prędkościami średnimi w danym przekroju

określonymi z równania ciągłości

v

śr

=Q/A

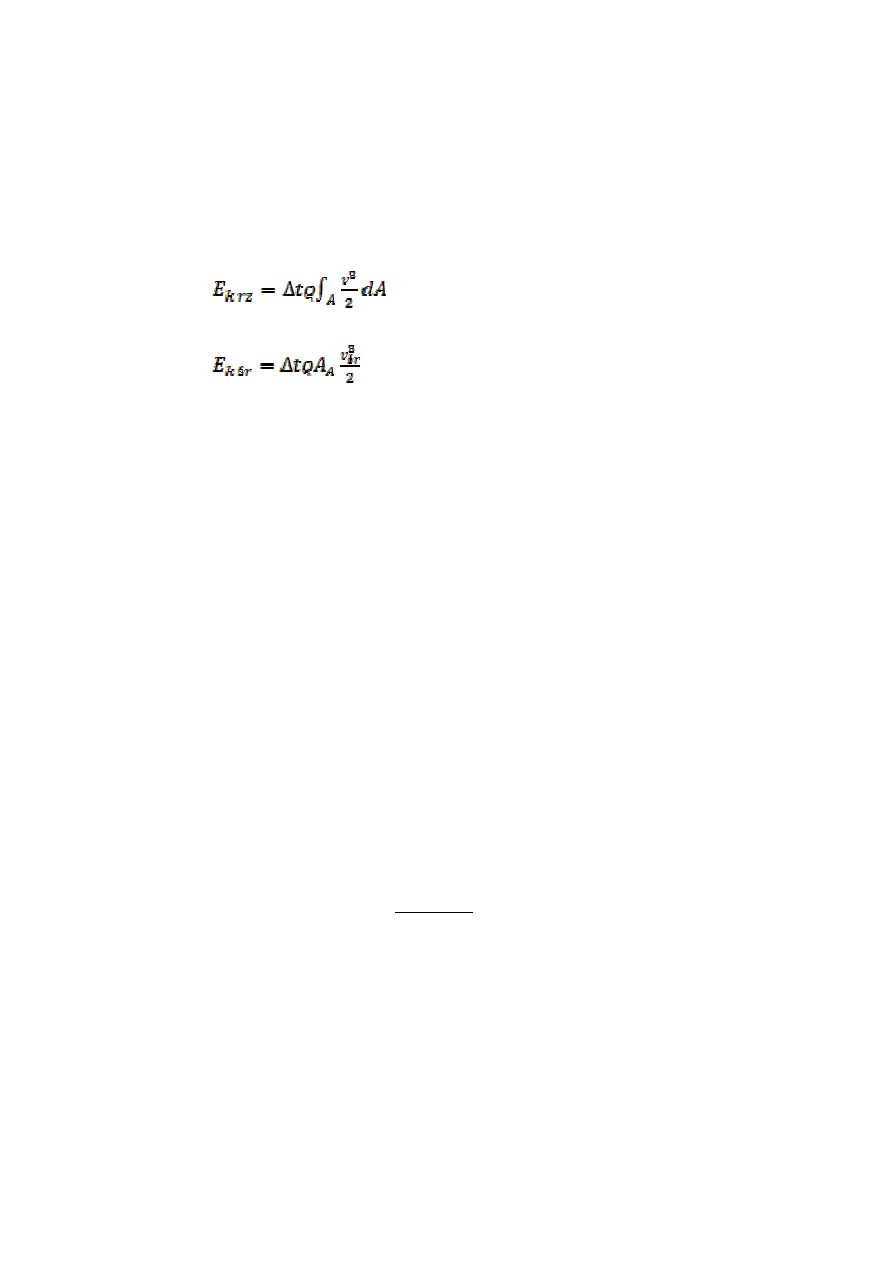
8

Ponieważ tę wielkość wykorzystujemy do określenia energii kinetycznej

więc wprowadzamy tzw. współczynnik Coriolisa zdefiniowany jako

α=E

k rz

/E

k śr

gdzie:

- rzeczywista wartość energii kinetycznej w

przekroju A

- wartość energii kinetycznej obliczona przy

pomocy prędkości średniej

W dalszej części będziemy operować tylko prędkościami średnimi
więc opuścimy indeks śr.

Δh

12

oznacza wielkość energii mechanicznej zamienioną na ciepło, w trakcie

przepływu płynu z przekroju 1 do 2, którą w przypadku cieczy możemy uznać
za straconą.

STRATY PRZEPŁYWU W PRZEPŁYWIE CZYNNIKA

RZECZYWISTEGO PRZEZ PRZEWODY

Całą wielkość strat Δh

12

dzieli się umownie na dwie części:

Δh

t

- stratę powstałą w wyniku tarcia o ścianki przewodu na długości l,

zwaną stratą tarcia lub stratą liniową,

Δh

m

- stratę powstałą w miejscach gdzie następuje zmian wektora

prędkości średniej, zwaną stratą miejscową lub lokalną (np. łuki,
zawory, miejsca zmiany wielkości i kształtu przekroju).

Δh

12

= Δh

t

+ Δh

m

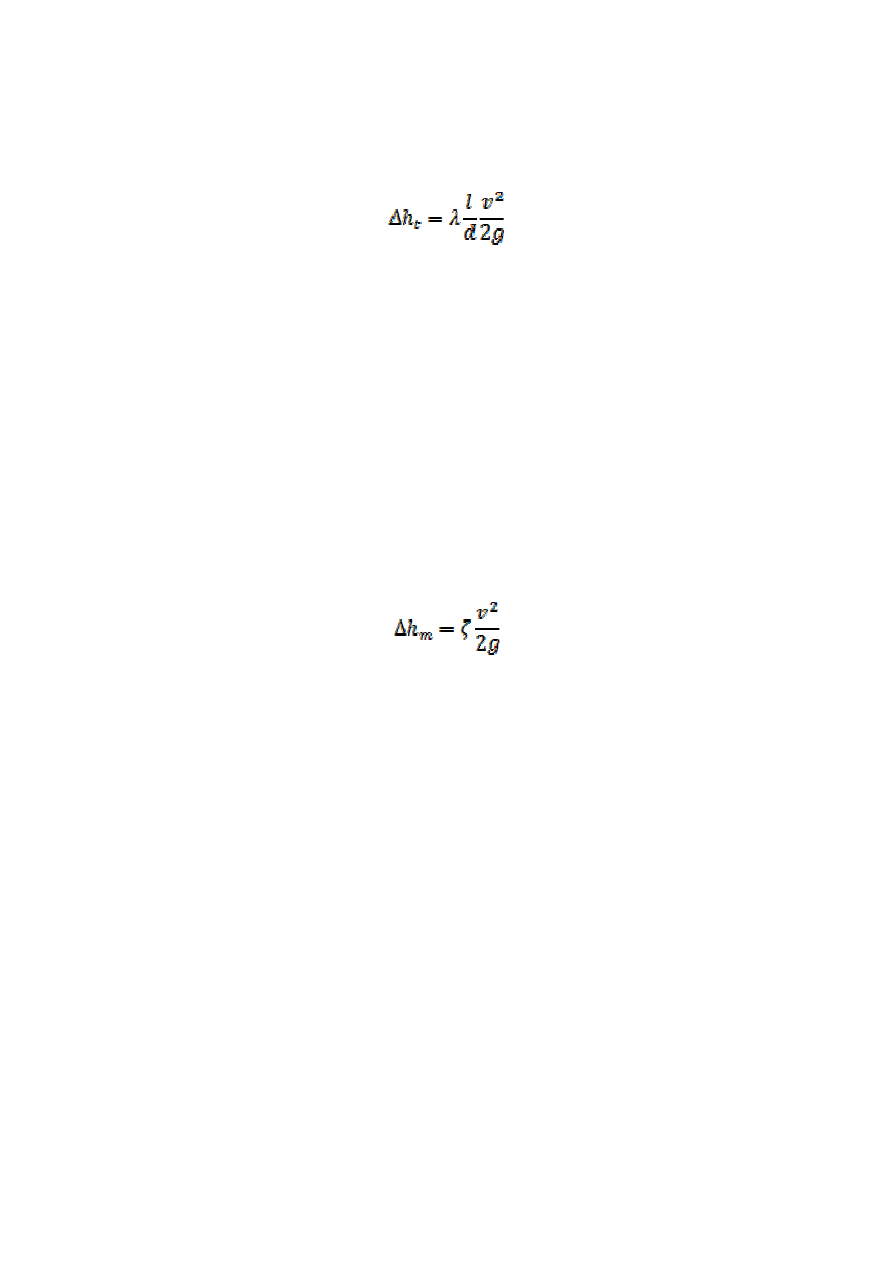
9

Stratę energii wywołaną tarciem (liniowych strat energii) wyrażoną jako
wysokość określa wzór Darcy’ego–Weisbacha

gdzie:

l – długość przewodu,
d – średnica przewodu,
v – średnia prędkość przepływu,
λ – współczynnik strat tarcia.

Współczynnik strat tarcia jest określany doświadczalnie jako

λ =f(Re, k/d)

gdzie:

k – średnia chropowatość ścianki rury (tzw. chropowatość
hydrauliczna).

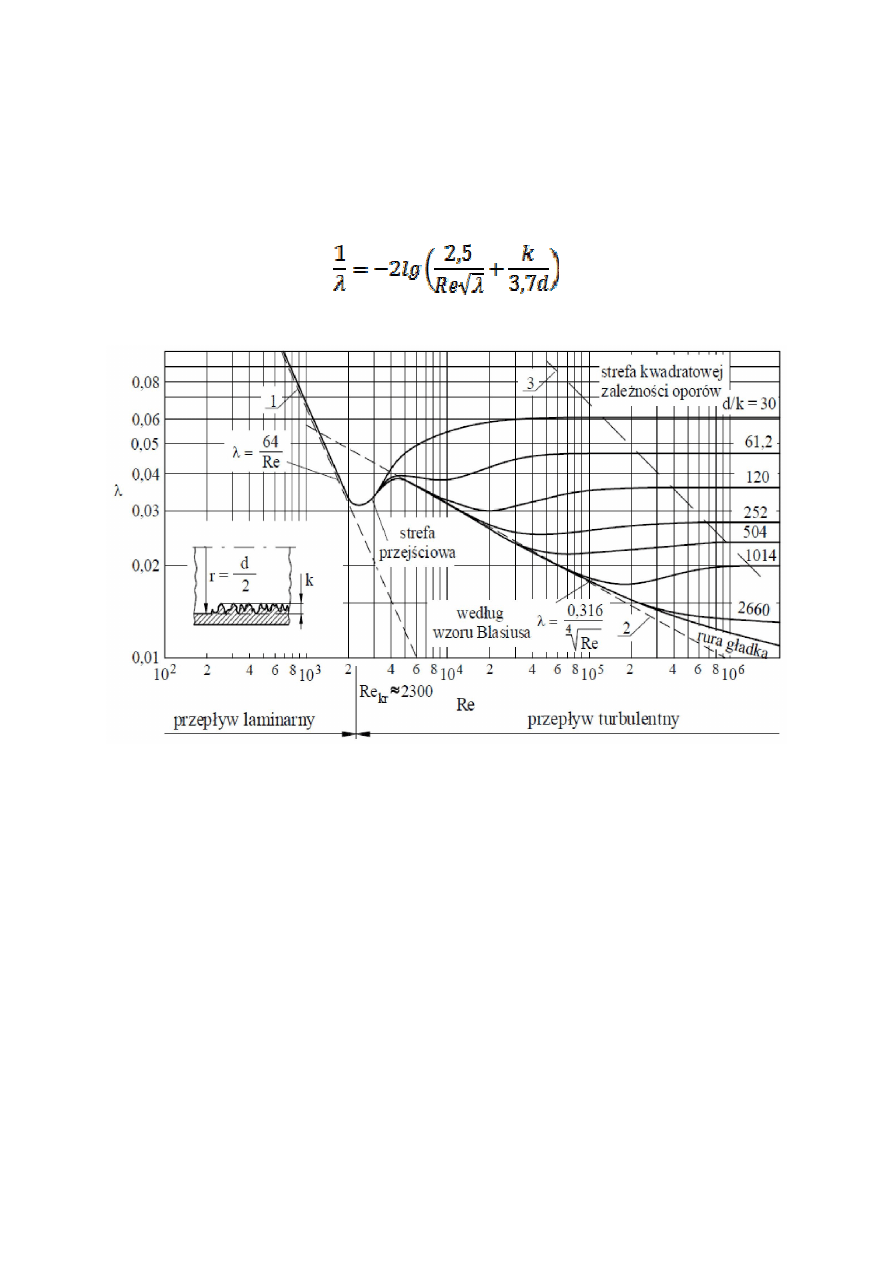
Wysokość strat miejscowych określa się z wzoru

gdzie:

ζ=f(Re) jest współczynnikiem strat charakterystycznym dla danego
elementu

Porównując wzory na oba rodzaje strat można wprowadzić pojęcie długości
równoważnej dla danego elementu zdefiniowanej wzorem

l

r

=(ζ/λ)d

określającej długość odcinka prostoosiowej rury o oporze równym oporowi
danej przeszkody miejscowej.

Dla przepływów przez kanały o przekrojach odbiegających od kształtu
kołowego korzysta się z tych samych zależności podstawiając zamiast średnicy
przewodu wartość tzw. średnicy hydraulicznej przewodu

D

h

= 4A/U

gdzie

U – długość zwilżonego obwodu

10

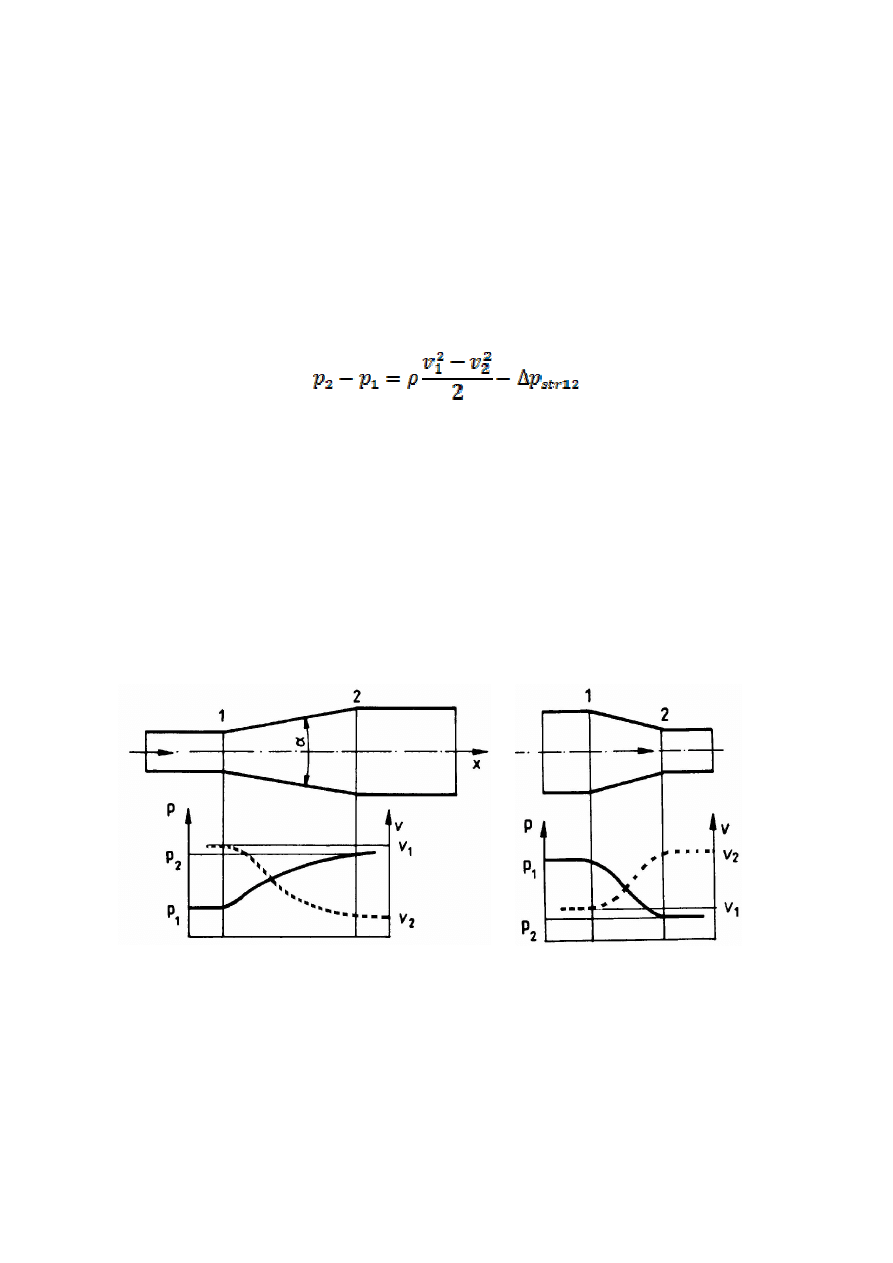
Wartości współczynnika strat tarcia określa się z zależności empirycznych np.
wykresu Nikuradsego, wzoru Colebrooka -- White’a, lub innych.

Wzór Colebrooka - White’a

Zależność

współczynnika oporu liniowego od liczby Reynoldsa – poglądowa

postać wykresu Nikuradsego

1 – wartości współczynnika dla przepływu laminarnego,

2 – wartości współczynnika dla przepływu turbulentnego przez rurę

hydraulicznie gładką,

3 – granica powyżej, której wartość współczynniki nie zależy od liczby Re.

11

Na wykresie można wyodrębnić kilka stref:

- strefa przepływu laminarnego poniżej krytycznej wartości liczby Re, w której
można dość precyzyjnie określić wartość współczynnika wzorem otrzymanym z
analizy naprężeń występujących w przepływie laminarnym;

- strefa przejściowa w której przepływ może przybierać różne formy zależnie od
wielkości zakłóceń występujących w przepływie; w praktyce przyjmuje się, że
w tym obszarze przepływ jest turbulentny;

- strefa przepływu w rurze hydraulicznie gładkiej, gdzie wartość współczynnika
jest zależna jedynie od liczby Re; chropowatość w tym przypadku jest na tyle
mała, że wielkość nierówności jest przykryta przez laminarną (najbliższą
ścianki) część warstwy przyściennej;

- strefa częściowego wpływu chropowatości na wartość współczynnika w której
λ =f(Re, k/d) ;
- strefa w pełni rozwiniętego przepływu turbulentnego w której λ =f(k/d), tzw.
strefa kwadratowej zależności strat.

Przykładowe wartości chropowatości niektórych przewodów

12

Wykres do określania wartości współczynnika strat tarcia

13

KANAŁY SPRĘŻAJĄCE I ROZPRĘŻAJĄCE

Z równania ciągłości wynika, że prędkość przepływu cieczy jest odwrotnie
proporcjonalna do pola przekroju kanału

v=Q/A

Z równania Bernoulliego wynika, że zmiana prędkości skutkuje zmianą
ciśnienia, którą dla poziomego kanału i cieczy rzeczywistej można określić jako:

gdzie

Δp

str12

– strata ciśnienia w wyniku tarcia na drodze od 1 do 2.

Dyfuzor - kanał sprężający. Przekrój kanału rośnie, prędkość maleje i ciśnienie
rośnie.

Konfuzor – kanał rozprężający. Przekrój kanału maleje, prędkość rośnie i
ciśnienie maleje

a)

b)

Dyfuzor stożkowy (a) i konfuzor stożkowy (b); kształt kanału oraz wykres

przebiegu ciśnienia (linia ciągła) oraz prędkości (linia przerywana).



kąt

rozwarcia dyfuzora

14

Przy przepływie cieczy rzeczywistej (lepkiej) charakter przepływu ma wpływ na
rozkład prędkości na przekroju kanału.

W kanałach sprężających (dyfuzorach)

dp/dx>0

więc elementy płynu znajdujące się w obszarze warstwy przyściennej są
hamowane nie tylko przez naprężenia styczne na ściankach, ale również
dodatkowo przez naprężenia normalne skierowane przeciwnie do kierunku
przepływu.
W rezultacie występują stosunkowo grube warstwy przyścienne, a więc i duże

straty. Przy zbyt dużym rozwarciu dyfuzora (duży kąt ) może dojść do
oderwania warstwy przyściennej co skutkuje znaczącym wzrostem strat.

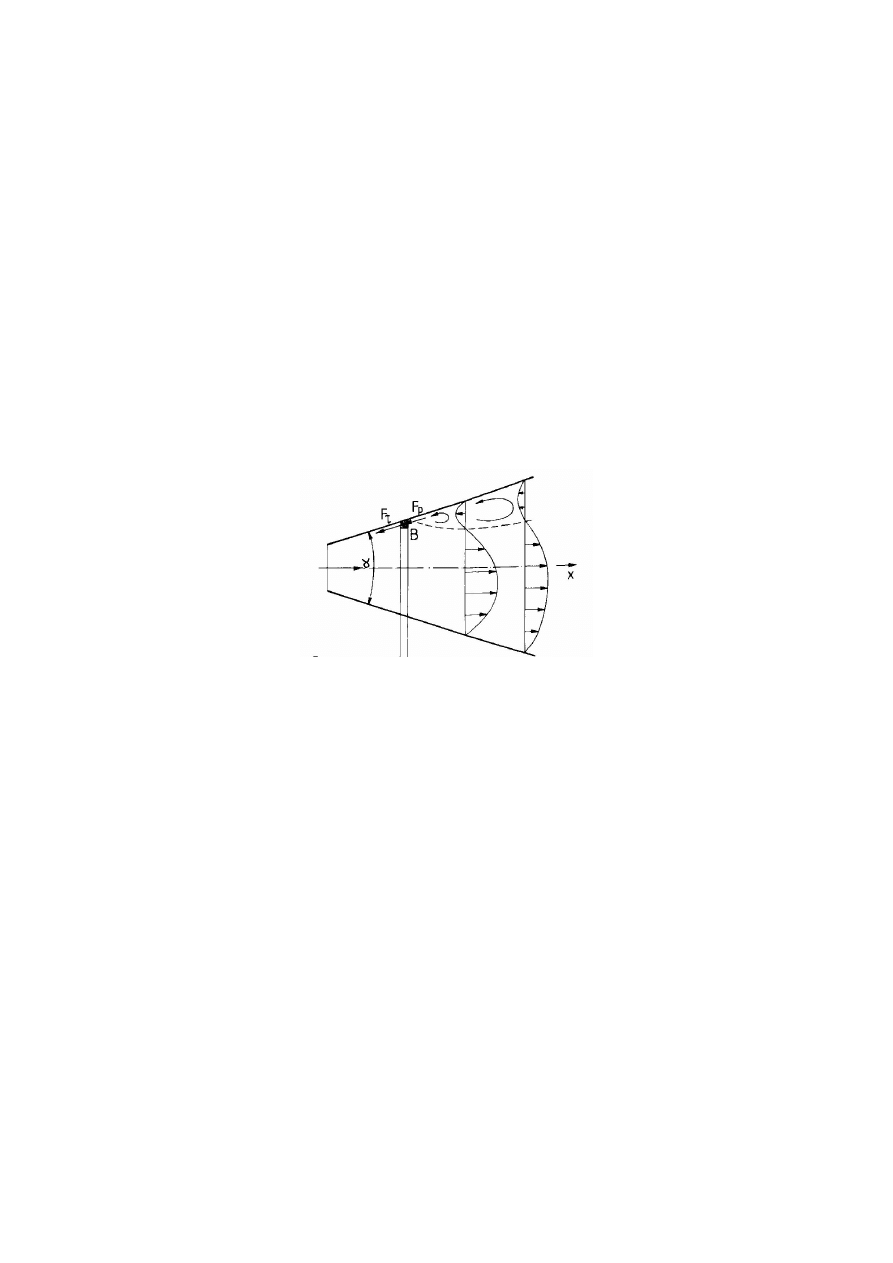
Przepływ w dyfuzorze z oderwaniem warstwy przyściennej. F





- siła tarcia

działająca na element płynu B, F

p



- siła od ciśnienia działająca na ten element

W kanałach rozprężających (konfuzorach)

dp/dx<0

więc elementy płynu znajdujące się w obszarze warstwy przyściennej są
popychane w kierunku przepływu. W rezultacie warstwy przyścienne są
stosunkowo cienkie i straty przepływu małe.