1

Fundamentowanie - ćwiczenia

Część 7 – Osiadanie pali – według normy PN-83/B-02482

(dr hab. inż. Adam Krasiński)

7.1. Osiadanie pala pojedynczego

Ogólnie osiadanie pala pojedynczego można obliczyć według wzoru normowego:

w

n

I

E

h

Q

s

⋅

⋅

=

0

w którym:

Q

n

– obciążenie pala, o wartości charakterystycznej⋅

h

– zagłębienie pala w gruncie

I

w

– współczynnik wpływu osiadania

E

0

– moduł odkształcenia gruntu wokół pala

Wartość współczynnika wpływu osiadania I

w

i sposób jego wyznaczania zależy od kilku czynników,

miedzy innymi warunków gruntowych, stosunku h/D, technologii wykonania pala, materiału trzonu

pala itp.

a) w przypadku pala w gruncie jednorodnym (E

0

= const.):

h

ok

w

R

I

I

⋅

=

I

ok

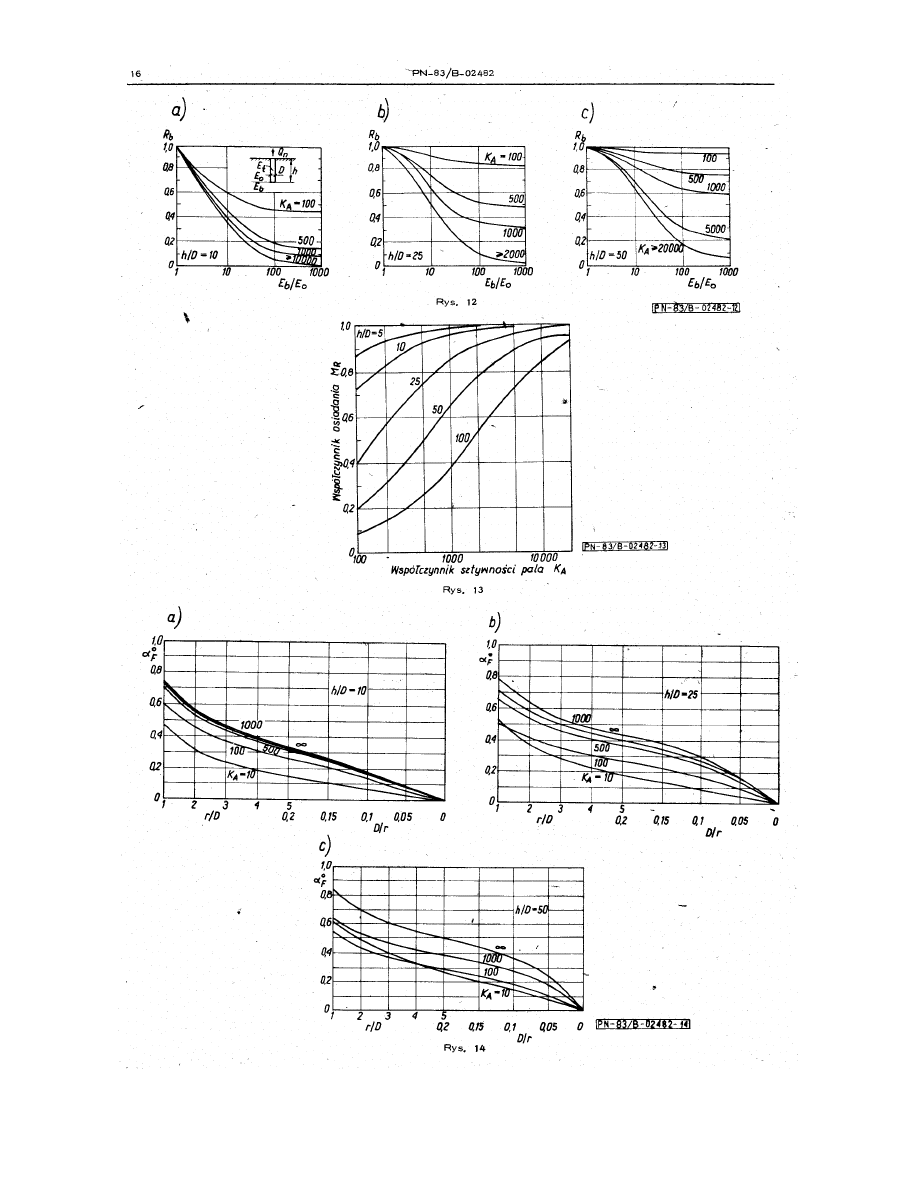
– współczynnik zależny od h/D i K

A

, odczytywany z nomogramu na rys. 10 w normie

A

t

A

R

E

E

K

⋅

=

0

,

E

t

– moduł ściśliwości trzonu pala, R

A

= A

tnt

/A

tbr

(dla pali betonowych pełnych R

A

= 1)

R

h

– współczynnik uwzględniający wpływ warstwy nieodkształcalnej (skały) na pewnej

głębokości poniżej podstawy pala, przyjmowany wg rysunku 11 normy; w przypadku
występowania tej warstwy R

h

< 1.0, a w przypadku jej braku – R

h

= 1

b) w przypadku pala w gruncie uwarstwionym

- dla gruntów o zbliżonych właściwościach należy E

0

przyjąć jako średnią ważoną do

głębokości h + 2D

- dla podłoża w warstwami słabymi w górnej części – h liczy się od stropu warstw nośnych, a

do wartości osiadania s dodaje się skrócenie własne trzonu pala na odcinku w warstwach

słabych,

- E

0

– można wyznaczyć metodą wsteczną z próbnego obciążenia pala

c) w przypadku pala z warstwą mniej ściśliwą pod podstawą pala

b

ok

w

R

I

I

⋅

=

R

b

– współczynnik wpływu warstwy mniej ściśliwej w podstawie pala odczytywany z rys. 12

normy w zależności od h/D, K

A

i E

b

/E

0

.

E

b

– moduł odkształcenia gruntu pod podstawą pala

d) w przypadku pala z podstawą na warstwie nieodkształcalnej (na skale) (E

b

/E

0

> 1000) osiadanie

oblicza się ze wzoru:

R

tnt

t

n

M

A

E

h

Q

s

⋅

⋅

⋅

=

2

M

R

– współczynnik osiadania – według rys. 13, M

R

≤ 1.0

Uwzględnianie technologii wykonawstwa pali w obliczaniu osiadań
Technologię wykonawstwa pali uwzględnia się przez przemnożenie modułów odkształcenia gruntu E

0

przez współczynniki technologiczne :

-

moduł gruntu wzdłuż pobocznicy pala: E

0s

= S

s

⋅E

0

-

moduł gruntu pod podstawą pala: E

0b

= S

p

⋅E

0

S

s

i S

p

– współczynniki technologiczne odczytywane z tabl. 4 normy, za wyjątkiem pali wierconych,

dla których przyjmuje się S

p

= S

s

= 0.8.

7.2. Osiadanie grupy pali

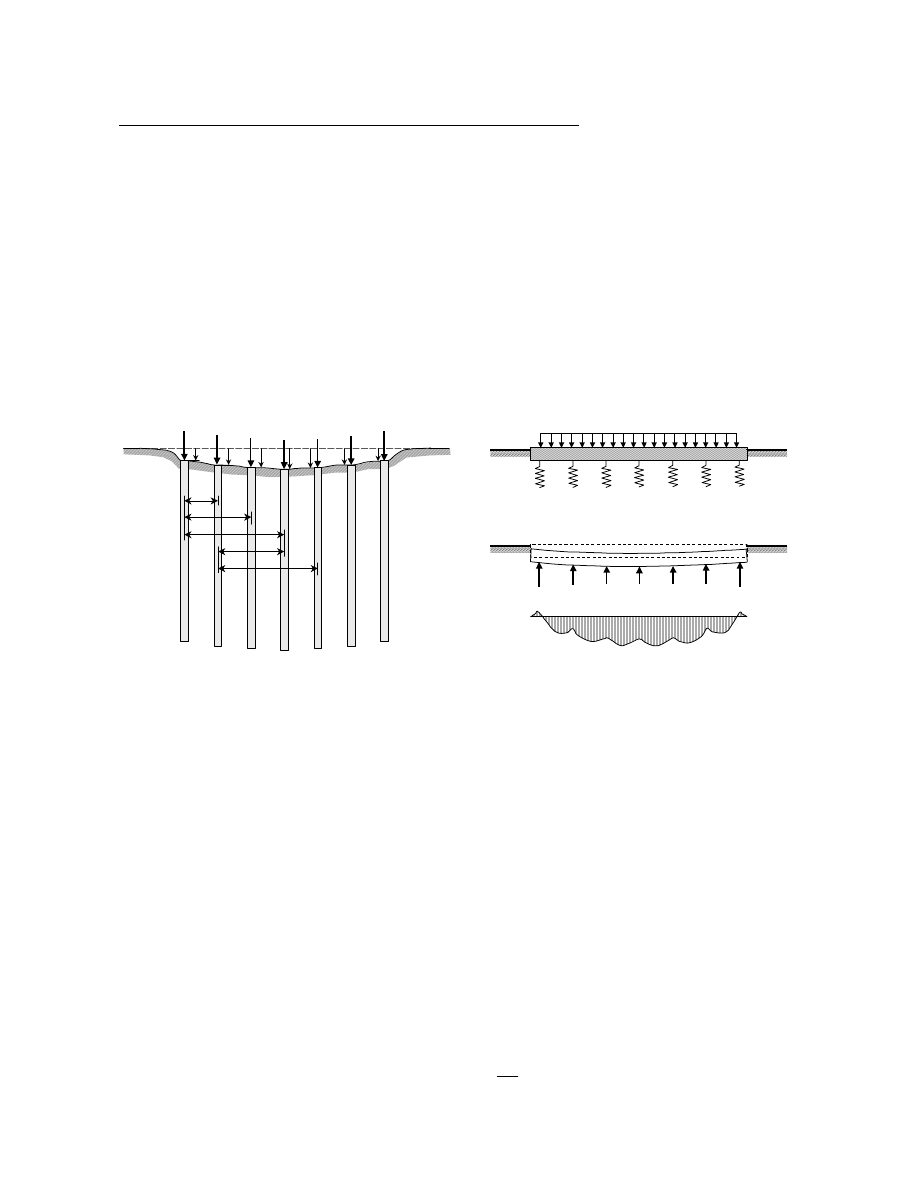
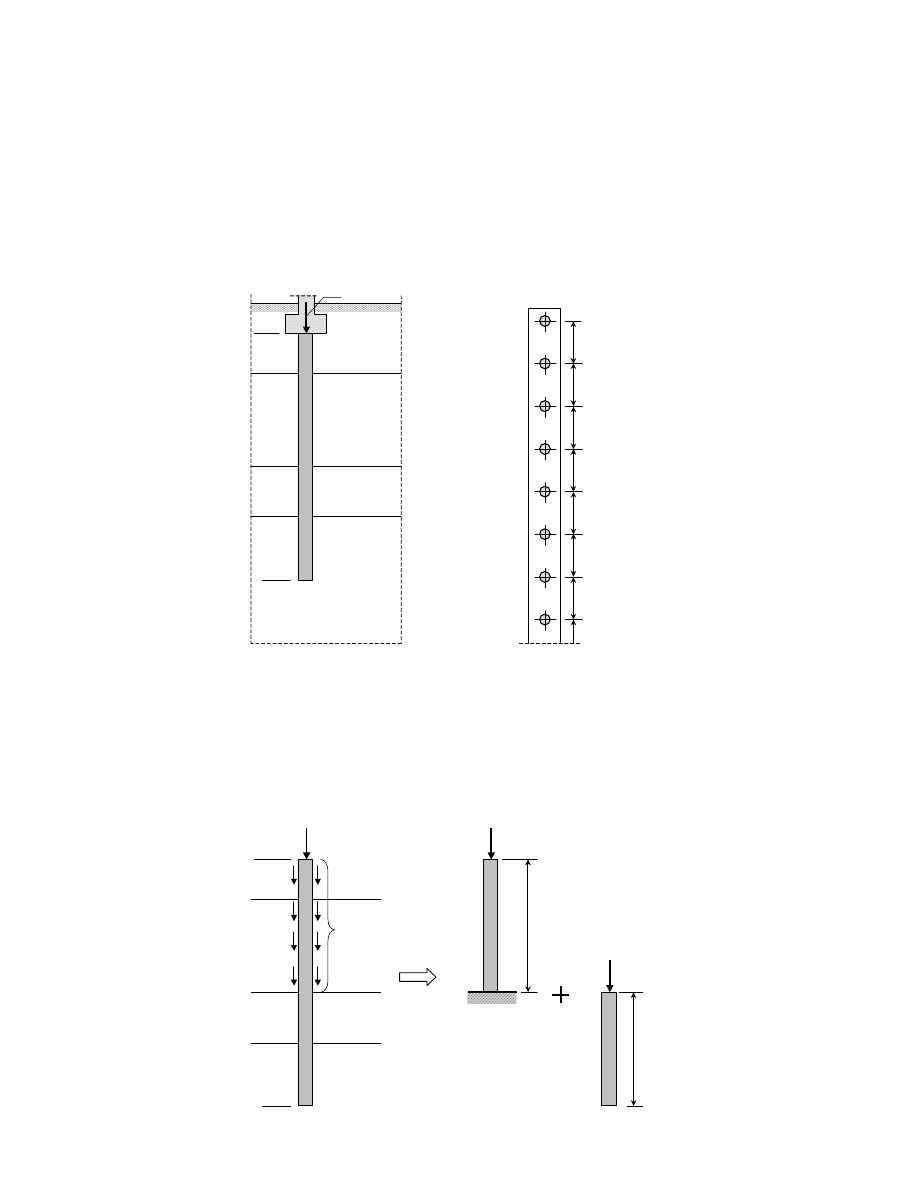
Osiadanie grupy pali jest zawsze większe niż pala pojedynczego, a ponadto jest nierównomierne – pale
na brzegach grupy osiadają najmniej, a pale w środku – najwięcej. Ta nierównomierność jest jednak w
dużej mierze tłumiona przez sztywność oczepu fundamentowego, ale kosztem jego zwiększonego
zginania (patrz rysunek poniżej).

Rys. Schemat osiadania grupy pali i jego wpływ na pracę fundamentu palowego.

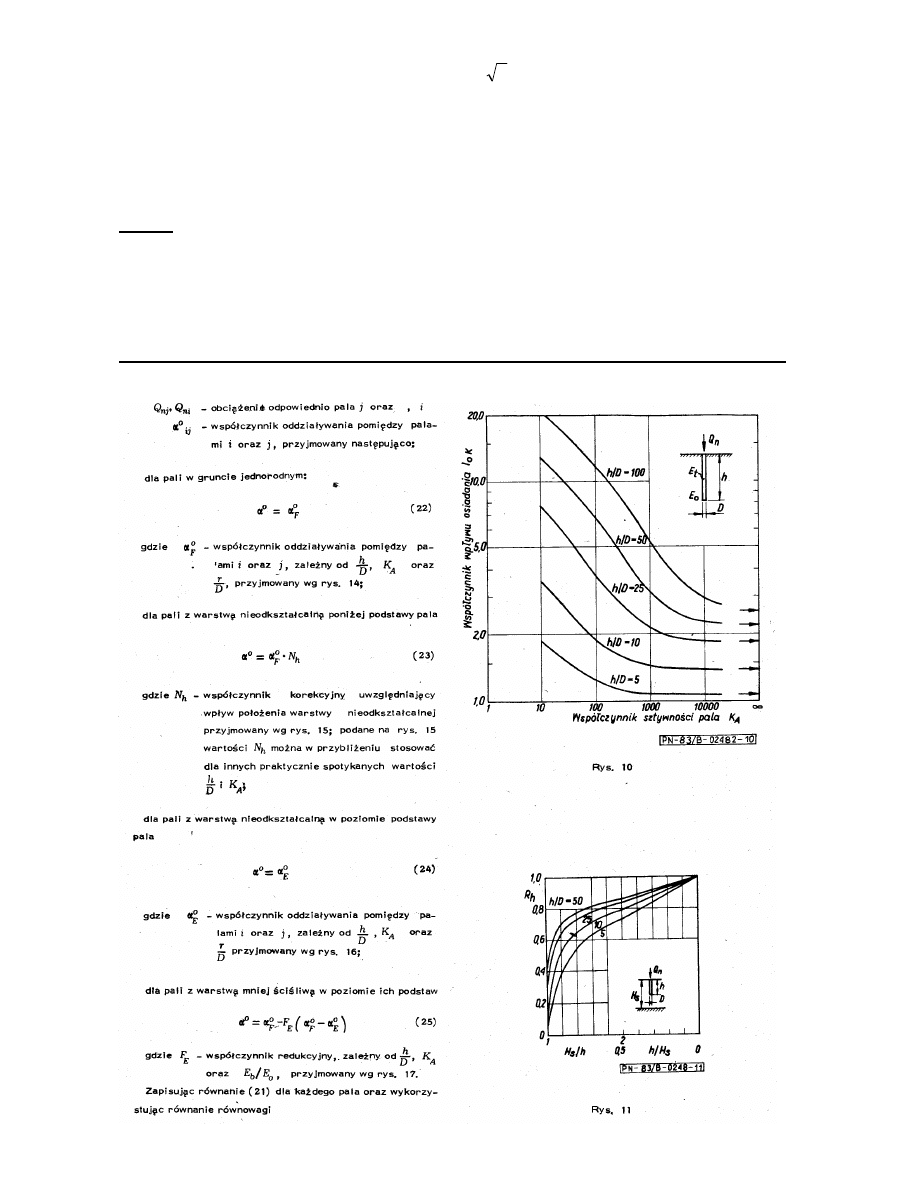
Osiadanie pala „i” w grupie liczącej „k” pali oblicza się według wzoru:

∑

=

+

⋅

=

k

j

i

ij

j

i

s

)

s

(

s

1

0

α

, dla j ≠ i

0

ij

α

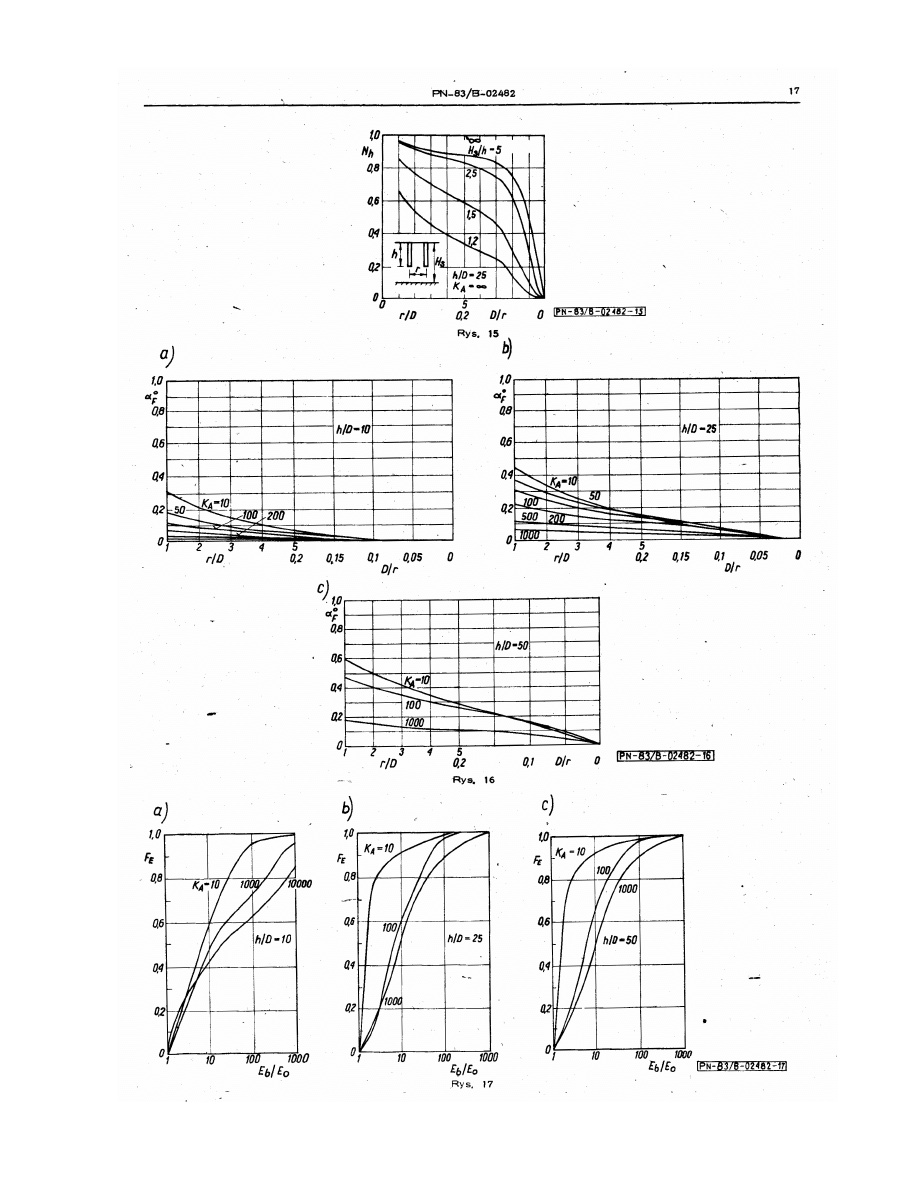
- współczynnik oddziaływania pomiędzy palami „i” oraz „j”, odczytywany z odpowiednich

nomogramów normowych na podstawie h/D, K

A

oraz r

ij

/D.

r

ij

– odległość w linii prostej pomiędzy palami „i” oraz „j” (rys. powyżej).

Im większe r

ij

tym mniejsze

0

ij

α

i dlatego pale środkowe osiadają najwięcej.

7.3. Przybliżona metoda szacowania osiadań pali

Osiadania pali można zgrubnie oszacować, wykorzystując przybliżoną prawidłowość, że nośność N

t

pala mobilizuje się przy jego osiadaniu równym około 0.01 średnicy podstawy pala D

p

, co

potwierdzają liczne badania pali w terenie (próbne obciążenia). Osiadanie pala pojedynczego
obciążonego siłą charakterystyczną Q

n

≤ N

t

można więc określić z zależności:

t

n

N

Q

D

s

⋅

=

01

.

0

1

Osiadanie grupy pali można oszacować następnie wykorzystując propozycję Van Impe:

q

K

z1

K

z2

K

z3

K

z4

K

z5

K

z6

K

z7

Q

1

Q

2

Q

3

Q

4

Q

5

Q

6

Q

7

[M]

Q

Q

Q

Q

Q

Q

Q

s

1

s

2

s

3

s

4

s

5

s

6

s

7

(1)

(2)

(3)

(4)

(5)

(6)

(7)

r

1,2

(r

2,1

)

r

1,3

(r

3,1

)

r

1,4

(r

4,1

)

r

2,4

(r

4,2

)

r

2,5

(r

5,2

)

3

n

s

s

gr

⋅

=

1

w którym n jest liczbą pali w grupie. Należy zaznaczyć, że s

gr

określa maksymalne osiadanie pala

w grupie (pala środkowego) i odnosi się raczej do zwartej grupy pali (np. kołowej lub kwadratowej) w
regularnej siatce pali (np. kwadratowej lub trójkątnej równobocznej) i w miarę równomiernie
obciążonych. Osiadanie pala na brzegu grupy jest mniejsze i wynosi około 0.65s

gr

. Zmienność osiadań

pali pośrednich, pomiędzy środkiem a brzegiem, można przyjąć paraboliczną.

Uwaga. Należy zaznaczyć, że powyższe propozycje szacowania osiadań pali dotyczą grup pali nie
związanych oczepem fundamentowym, a więc przy założeniu swobodnej możliwości osiadania
każdego z pali. W rzeczywistości kształt osiadań pali jest krępowany sztywnością oczepu. Fakt taki
należy uwzględnić stosując obliczenie fundamentu jako rusztu lub płyty o określonej sztywności na
sprężystych podporach palowych o nierównomiernej sztywności.

Wybrane fragmenty normy palowej, dotyczące obliczania osiadań pali i fundamentów na palach

4

5

6

Zadanie przykładowe nr 7.1

1. Dane wyjściowe

Przyjęto pale wiercone φ500 mm, rozmieszczone w jednym rzędzie w rozstawie co r = 2.0 m.

Obciążenia pali:

- siła zewnętrzna charakterystyczna: Q

n

= 1000 kN,

- tarcie negatywne: T

n

= 120 kN

Beton pala: B25 → E

t

= 30000 MPa

2. Osiadanie pala pojedynczego

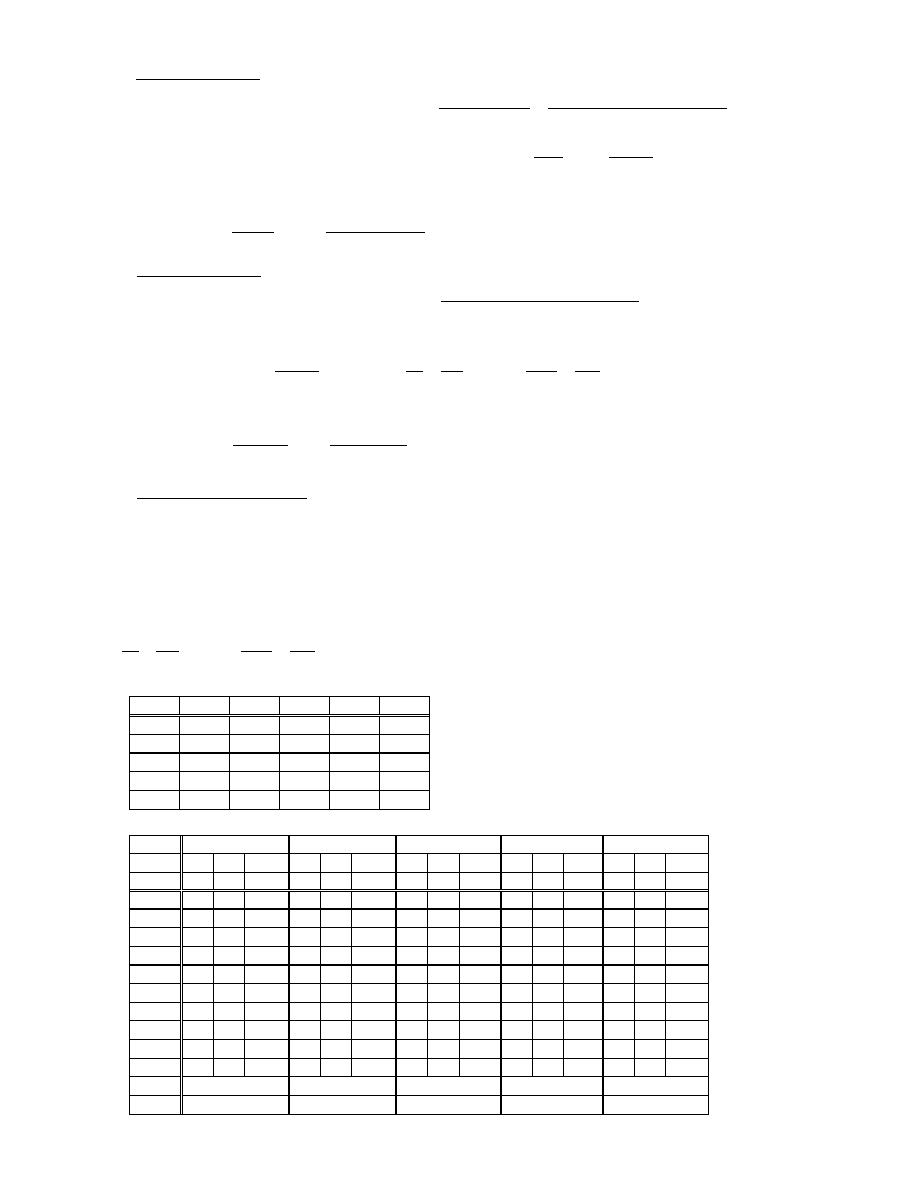
Ze względu na uwarstwione podłoże gruntowe oraz tarcie negatywne pal podzielono na dwa pale

składowe (rys. poniżej):

- pal (1) – pal na podłożu nieściśliwym pod podstawą (tak jak na skale)

- pal (2) – pal w podłożu uwarstwionym z warstwą mniej ściśliwą pod podstawą

Osiadanie całkowite pala będzie sumą osiadań pali (1) i (2).

0.0

-1.5

-3.5

-7.5

-10.0

-12.5

Gp, gen. C
I

L

= 0.35

E

0

= 12 MPa

T/Nm
E

0

= 1.0 MPa

Pg, gen. C
I

L

= 0.20

E

0

= 20 MPa

Ps,
I

D

= 0.70

E

0

= 110 MPa

Q

n

2.0

2.0

2.0

2.0

2.0

2.0

2.0

1

2

3

4

5

6

7

8

Przekrój pionowy z profilem geotechnicznym

Plan fundamentu palowego

-1.5

-3.5

-7.5

-10.0

-12.5

Gp

T/Nm

Pg

Ps

Q

n

T

n

Q

n

Q

n

+ T

n

h

1

= 6.0 m

h

2

= 5.0 m

pal (1)

pal (2)

7

a) Osiadanie pala (1)

Uśredniony moduł gruntu wzdłuż pala:

3

4

0

6

0

4

0

1

0

1

0

2

0

12

9

0

0

1

0

.

.

.

.

.

.

.

.

h

h

E

S

E

i

i

i

si

s

=

⋅

⋅

+

⋅

⋅

=

⋅

⋅

=

∑

∑

MPa

Pal o pełnym kształcie →

0

1.

R

A

=

, współczynnik

7000

0

1

3

4

30000

1

0

1

≈

⋅

=

⋅

=

.

.

R

E

E

K

A

s

t

A

Przekrój pala:

196

0

5

0

25

0

2

.

.

.

A

t

=

⋅

=

π

m

2

,

0

12

5

0

0

6

1

.

.

/

.

D

/

h

=

=

→

99

0.

M

R

=

przyjęto

0

1.

M

R

=

Osiadanie:

3

7

1

1

10

02

1

196

0

10

0

3

0

6

1000

−

⋅

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

.

.

.

.

M

A

E

h

Q

s

R

t

t

n

m = 1.02 mm

b) Osiadanie pala (2)

Uśredniony moduł gruntu wzdłuż pala:

0

53

0

5

5

2

0

110

8

0

5

2

0

20

9

0

2

0

.

.

.

.

.

.

.

.

E

s

=

⋅

⋅

+

⋅

⋅

=

MPa

Moduł gruntu pod podstawą pala:

110

110

0

1

0

=

⋅

=

⋅

=

.

E

S

E

p

b

MPa

Współczynniki:

566

0

1

0

53

30000

1

=

⋅

=

.

.

K

A

,

0

10

5

0

0

5

2

.

.

.

D

h

=

=

,

08

2

53

110

2

0

.

E

E

s

b

=

=

→

5

1

0

.

I

k

=

,

75

0.

R

b

=

13

1

75

0

5

1

0

.

.

.

R

I

I

b

k

w

=

⋅

=

⋅

=

Osiadanie:

3

3

2

0

2

2

10

78

4

13

1

10

53

0

5

120

1000

−

⋅

=

⋅

⋅

⋅

+

=

⋅

⋅

+

=

.

.

.

I

E

h

T

Q

s

w

s

n

n

m = 4.78 mm

b) Osiadanie całkowite pala

s = s

1

+ s

2

= 1.02 + 4.78 = 5.80 mm

3. Osiadanie pali w grupie

Osiadanie pala „i” w grupie pali o liczbie „k” pali określa wzór:

∑

=

+

⋅

=

k

j

i

ij

j

gi

s

)

s

(

s

1

1

0

2

α

Współczynnik

)

(

F

Eij

Fij

E

Fij

ij

0

0

0

0

α

α

α

α

−

−

=

,

0

Fij

α

,

0

Fij

α

- odp. wg rys. 14 i 16 (PN),

0

ii

α

= 1.0

0

10

5

0

0

5

2

.

.

.

D

h

=

=

,

08

2

53

110

2

0

.

E

E

s

b

=

=

→

22

0.

F

E

≈

wg. rys. 17 (PN)

Tablica 1. Wyznaczenie współczynników α

α

α

α

0

ij

r

ij

[m]

2.0

4.0

6.0

8.0

10.0

r

ij

/D

4.0

8.0

12.0

16.0

20.0

D/r

ij

0.25

0.13

0.08

0.06

0.05

α

α

α

α

0

Fij

0.38

0.21

0.15

0.09

0.08

α

α

α

α

0

Eij

0.02

0.01

0

0

0

α

α

α

α

0

ij

0.30

0.17

0.12

0.07

0.06

W obliczeniach przyjęto, że wzajemne oddziaływanie pali na
siebie sięga do 4 pali w obu kierunkach.
Osiadania policzono dla 5 skrajnych pali fundamentu.

Tablica 2. Obliczenia osiadań pali w grupie

Pal "i"

1

2

3

4

5

r

ij

α

α

α

α

0

ij

α

α

α

α

0

ij

⋅⋅⋅⋅s

2j

r

ij

α

α

α

α

0

ij

α

α

α

α

0

ij

⋅⋅⋅⋅s

2j

r

ij

α

α

α

α

0

ij

α

α

α

α

0

ij

⋅⋅⋅⋅s

2j

r

ij

α

α

α

α

0

ij

α

α

α

α

0

ij

⋅⋅⋅⋅s

2j

r

ij

α

α

α

α

0

ij

α

α

α

α

0

ij

⋅⋅⋅⋅s

2j

Pal "j"

[mm]

[mm]

[mm]

[mm]

[mm]

1

0.0

1.00

4.78

2.0

0.30

1.43

4.0

0.17

0.81

6.0

0.12

0.57

8.0

0.07

0.33

2

2.0

0.30

1.43

0.0

1.00

4.78

2.0

0.30

1.43

4.0

0.17

0.81

6.0

0.12

0.57

3

4.0

0.17

0.81

2.0

0.30

1.43

0.0

1.00

4.78

2.0

0.30

1.43

4.0

0.17

0.81

4

6.0

0.12

0.57

4.0

0.17

0.81

2.0

0.30

1.43

0.0

1.00

4.78

2.0

0.30

1.43

5

8.0

0.07

0.33

6.0

0.12

0.57

4.0

0.17

0.81

2.0

0.30

1.43

0.0

1.00

4.78

6

10.0

0.06

0.29

8.0

0.07

0.33

6.0

0.12

0.57

4.0

0.17

0.81

2.0

0.30

1.43

7

12.0

-

-

10.0

0.06

0.29

8.0

0.07

0.33

6.0

0.12

0.57

4.0

0.17

0.81

8

14.0

-

-

12.0

-

-

10.0

0.06

0.29

8.0

0.07

0.33

6.0

0.12

0.57

9

16.0

-

-

14.0

-

-

12.0

-

-

10.0

0.06

0.29

8.0

0.07

0.33

10

20.0

-

-

16.0

-

-

14.0

-

-

12.0

-

-

10.0

0.06

0.29

s

1i

[mm]

1.02

1.02

1.02

1.02

1.02

s

gi

[mm]

9.24

10.68

11.49

12.06

12.40