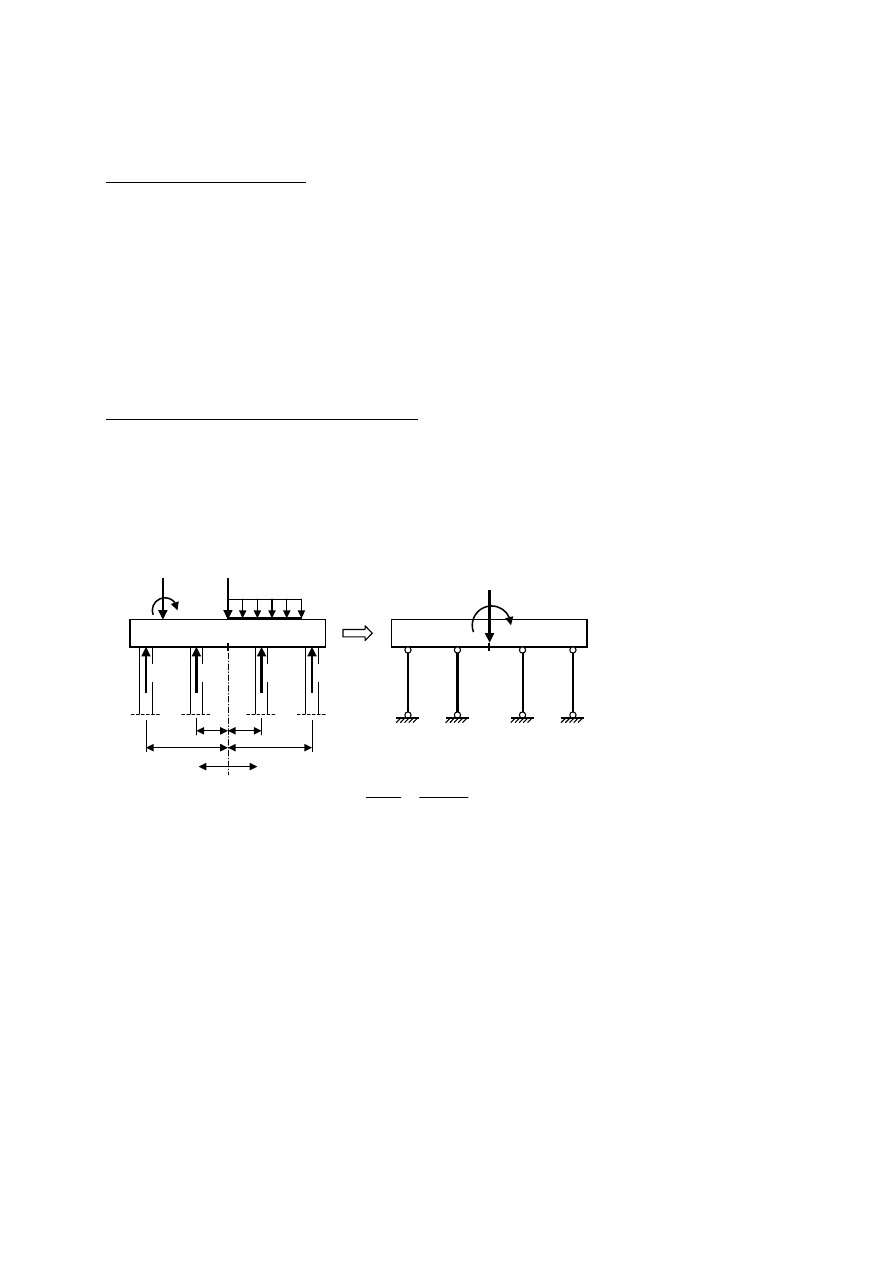
1
Fundamentowanie – ćwiczenia
Część 4 – Obliczanie statyczne fundamentów palowych – określanie sił w palach
(dr inż. Adam Krasiński, mgr inż. Tomasz Kusio)
Metoda sztywnego oczepu
W metodzie tej wprowadza się takie uproszczenia w schemacie obliczeniowym fundamentu
palowego, aby możliwe było jego rozwiązanie sposobem tzw. „ręcznym” (bez wykorzystywania
komputera).
Uproszczenia polegają na przyjęciu oczepu jako sztywnego bloku, natomiast pali jako prętów
obustronnie przegubowych (tzw. wahaczy). W wyniku obliczeń możemy otrzymać tylko siły
osiowe w palach (nie otrzymamy ani momentów zginających ani przemieszczeń). Momenty
w oczepie możemy w tej metodzie otrzymać metodą wtórną, w której siły w palach zamieniamy na
obciążenie, a słupy i ściany budowli stają się wówczas podporami (metoda odwróconego stropu).
Układy statyczne fundamentów palowych:
a) Układy dwuwymiarowe z palami tylko pionowymi (np. ława fundamentowa na palach)
Układy takie stosuje się przy obciążeniach tylko od sił pionowych i momentów, przy braku
obciążeń poziomych (zwykle obciążenia poziome można pominąć gdy ich suma jest mniejsza niż
10% sumy obciążeń pionowych, ale nie pomija się wówczas momentów od sił poziomych).
j
i
j
x
x
M
n
V
N
⋅
+
=
∑
∑
∑
2
0
, n – liczba pali
N
j
dodatnie – pale wciskane, N
j
- ujemne – pale wyciągane
V
1
V
2
M
1
q
N
1
N
2
N
3
N
4
0
x
2
x
1
x
3
x
4
x(-) x(+)
ΣV
ΣM
0
0
Uwagi:
1) punkt „0” – środek geome-
tryczny grupy pali
2) wszystkie pale jednakowe
Schemat
2
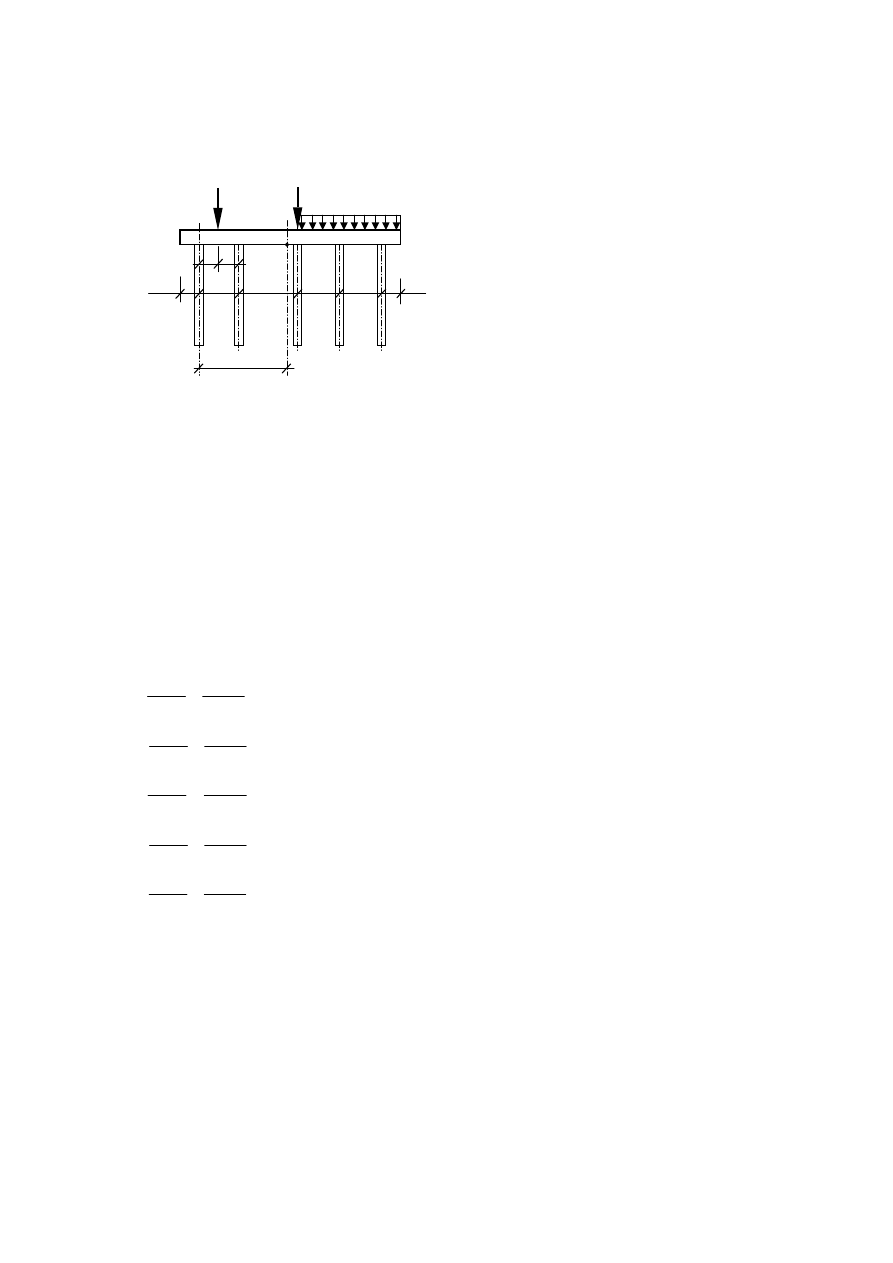
Zadanie przykładowe 4.1
Stosując metodę sztywnego oczepu policzyć siły w palach w fundamencie przedstawionym na
rysunku poniżej. Pominąć ciężar własny oczepu palowego.
Wyznaczenie położenia środka geometrycznego układu pali:
S
A
= 1
⋅0,0 + 1⋅2,0 + 1⋅5,0 + 1⋅7,0 + 1⋅9,0 = 23,0 m
x
0
= S
A
/n = 23,0/5 = 4,6 m
Obciążenia sprowadzone do punktu „0”:
ΣV = 1500 + 1000 + 300⋅5,0 = 4000 kN
ΣM
0
= -1500
⋅(4,6 – 1,0) + 1000⋅(5,0 – 4,6) + 300⋅5,0⋅(5,0 + 2,5 – 4,6) = – 650 kNm
Moment bezwładności układu pali względem punktu „0”:
Σx
i
2
= 4,6
2
+ (4,6-2)
2
+ (5,0 – 4,6)
2
+ (7,0 – 4,6)
2
+ (9,0 – 4,6)
2
= 53,2 m
2
Siły w poszczególnych palach:
856
)
6
,
4
(
2
,
53
650
5
4000
1
=
−
⋅
−
+
=
N
kN
832
)
0
,
2
6
,
4
(
2
,
53
650
5
4000
2
=
+
−
⋅
−
+
=
N
kN
795
)
6
,
4
0
,
5
(
2
,
53
650
5
4000
3
=
−
⋅
−
+
=
N
kN
771
)
6
,
4
0
,
7
(
2
,
53
650
5
4000
4
=
−
⋅
−
+
=
N
kN
746
)
6
,
4
0
,
9
(
2
,
53
650
5
4000
5
=
−
⋅
−
+
=
N
kN
P
1
=1500 kN
q=300 kN/m
3.0
1.0 2.0
2.0
1.0
2.0
P
2
=1000 kN
1.0 1.0
0
x
0
A
A
(1) (2)
(3) (4) (5)
3
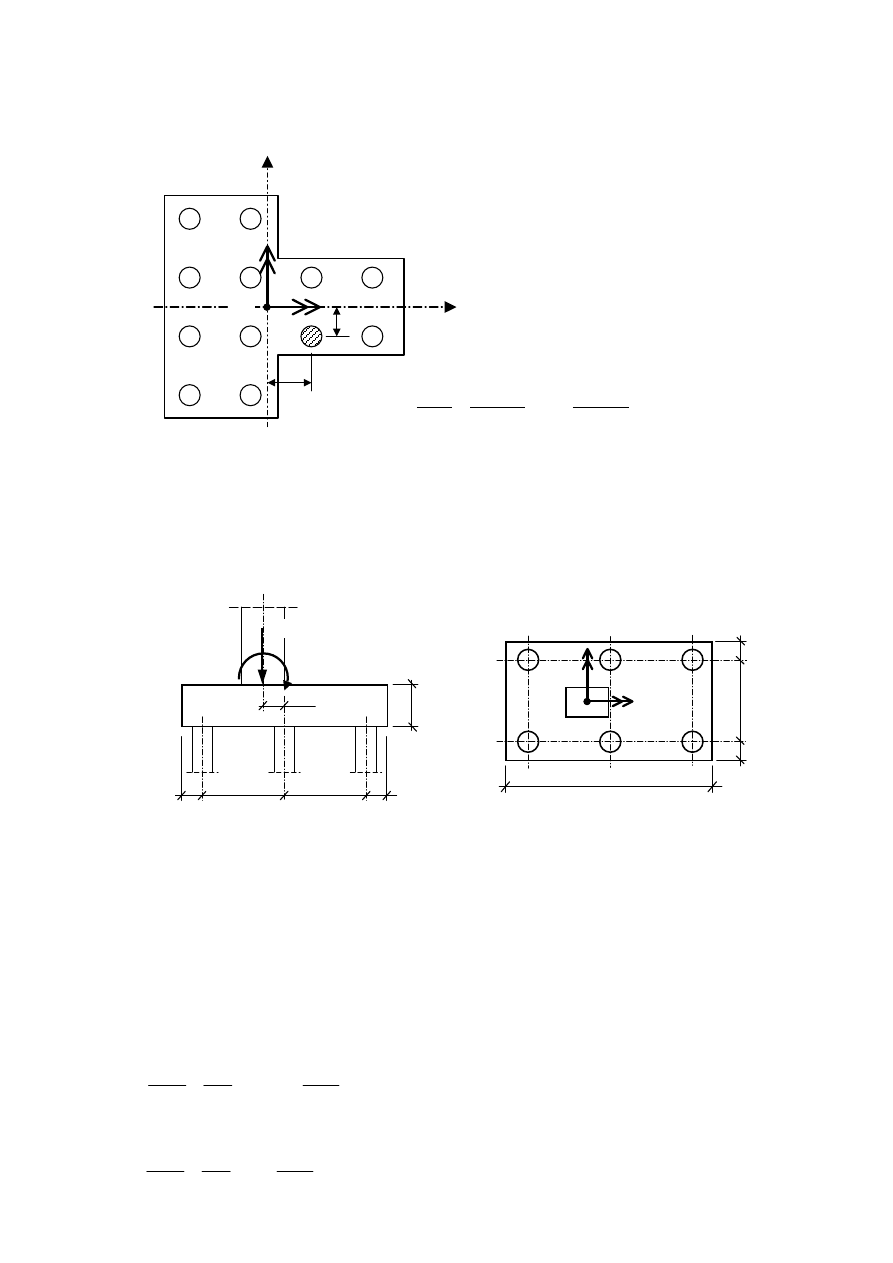
b) Układy trójwymiarowe z palami tylko pionowymi (np. stopa, płyta lub blok na palach)
Układy takie, podobnie jak wyżej, stosujemy przy obciążeniach tylko od sił pionowych
i momentów, przy braku lub pominięciu obciążeń poziomych.
j
i
y
j
i
x
j
x
x
M
y
y
M
n
V
N
⋅
+
⋅
−
=
∑
∑
∑
∑
∑
2
0
2
0
,
n – liczba pali
Zadanie przykładowe 4.2
Stosując metodę sztywnego oczepu policzyć siły w najbardziej obciążonym i w najmniej
obciążonym palu pod stopą fundamentową słupa budynku przemysłowego. Do obciążeń ze słupa
doliczyć ciężar własny stopy fundamentowej.
Obciążenia sprowadzone do punktu „0”:
Ciężar fundamentu: G
F
= 5,0
⋅3,0⋅0,8⋅25,0 = 300 kN
ΣV = 3500 + 300 = 3800 kN
ΣM
x0
= 800 kNm
ΣM
y0
= 2500 – 3500
⋅0,3 = 1450 kNm
Momenty bezwładności układu pali względem osi x
0
i y
0
:
Σx
i
2
= 4
⋅2,0
2
= 16 m
2
;
Σy
i
2
= 6
⋅1,0
2
= 6 m
2
Siła w najbardziej obciążonym palu – nr 6:
=
⋅
+
−
⋅
−
=
)
0
,
2
(
0
,
16
1450
)
0
,
1
(
0
,
6
800
6
3800
6
N
948,0 kN
Siła w najmniej obciążonym palu – nr 1:
=
−
⋅
+
⋅
−
=
)
0
,
2
(
0
,
16
1450
0
,
1
0
,
6
800
6
3800
1
N
319,0 kN
x
i
y
i
ΣV
0
ΣM
y0
ΣM
x0
y
0
x
0
Uwagi:
1) punkt „0” – środek geome-
tryczny grupy pali
2) wszystkie pale jednakowe
3) znaki x i y według ćwiartek
układu współrzędnych
4) znaki M
x0
i M
y0
– dodatnie
gdy zgodne z osiami x i y
0
e
s
= 0,3 m
2,0 2,0
0,5 0,5
0,8
V
s
= 3500 kN
M
sy
= 2500 kNm
M
sx
= 800 kNm
M
sy
V
s
2,0
0,5
0,5
Przekrój pionowy
Plan
(1)
(2)
(3)
(4)
(5)
(6)
5,0
4
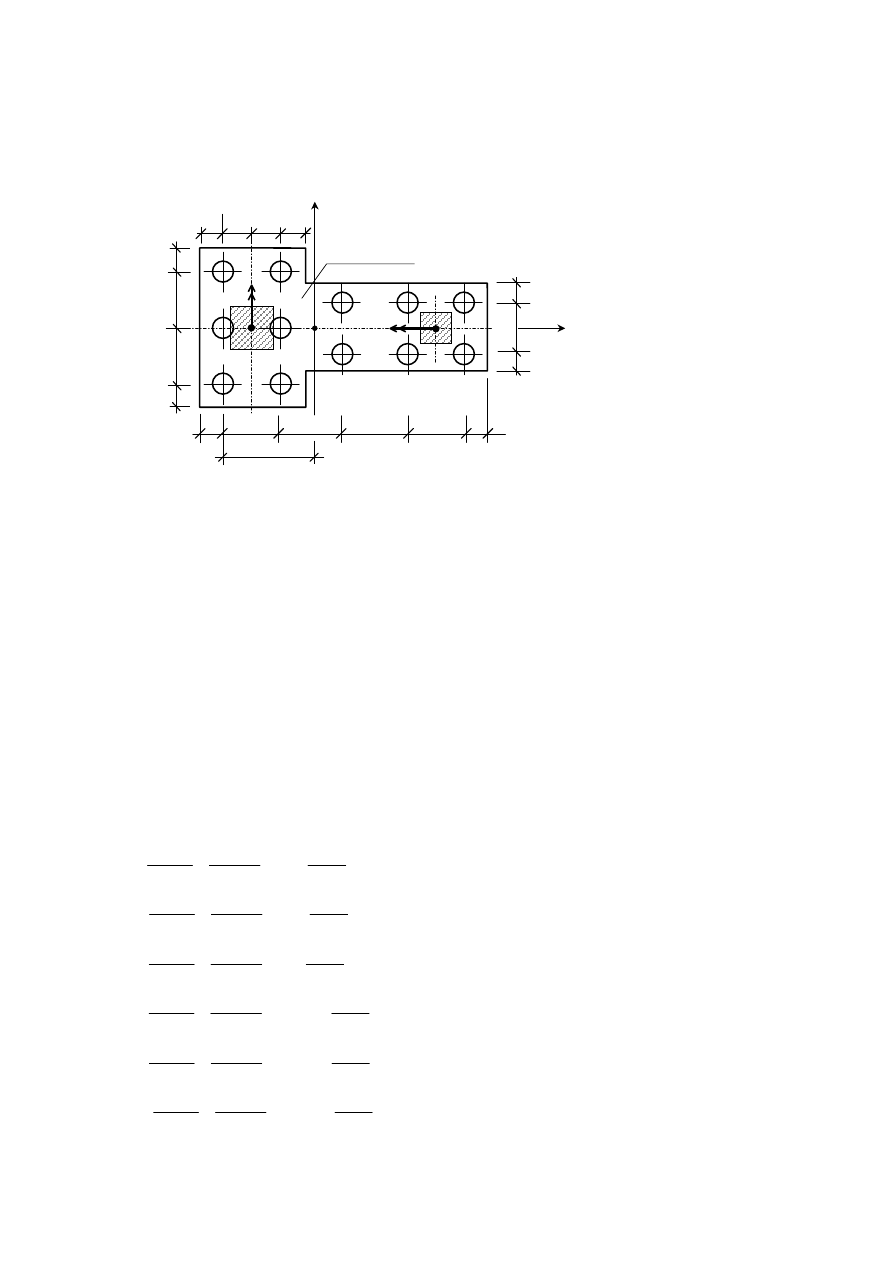
Zadanie przykładowe 4.3
Stosując metodę sztywnego oczepu policzyć siły w najbardziej obciążonym i w najmniej
obciążonym palu pod fundamentem dwóch słupów budynku szkieletowego. Do obciążeń ze słupów
doliczyć ciężar własny stopy fundamentowej.
Wyznaczenie położenia środka geometrycznego układu pali:
S
yA
= 3
⋅2,0 + 2⋅4,0 + 2⋅6,0 + 2⋅8,0 = 42,0 m
x
0
= 42,0/12 = 3,5 m
Obciążenia sprowadzone do punktu „0”:
Ciężar fundamentu: G
F1
= 4,0
⋅6,0⋅1,0⋅25,0 = 600 kN, G
F2
= 6,0
⋅4,0⋅1,0⋅25,0 = 600 kN
ΣV = 8000 + 5000 + 600 + 600 = 14200 kN
ΣM
x0
= –6000 kNm
ΣM
y0
= –8000
⋅2,5 + 5000⋅3,5 + 10000 – 600⋅3,5 + 600⋅3,5 = 7500 kNm
Momenty bezwładności układu pali względem osi x
0
i y
0
:
Σx
i
2
= 3
⋅3,5
2
+ 3
⋅1,5
2
+ 2
⋅0,5
2
+ 2
⋅2,5
2
+ 2
⋅4,5
2
= 97 m
2
Σy
i
2
= 2
⋅(2,2
2
+ 3
⋅1
2
) = 22 m
2
Siły w wybranych palach:
1458
)
5
,
3
(
0
,
97
7500
0
,
2
22
6000
12
14200
1
=
−
⋅
+
⋅
−
−
=
N
kN
1613
)
5
,
1
(
0
,
97
7500
0
,
2
22
6000
12
14200
2
=
−
⋅
+
⋅
−
−
=
N
kN
1618
5
,
4
0
,
97
3500
0
,
1
22
6000
12
14200
9
=
⋅
+
⋅
−
−
=
N
kN = N
max
512
)
5
,
3
(
0
,
97
3500
)
0
,
2
(
22
6000
12
14200
5
=
−
⋅
+
−
⋅
−
−
=
N
kN = N
min
584
)
5
,
1
(
0
,
97
3500
)
0
,
2
(
22
6000
12
14200
6
=
−
⋅
+
−
⋅
−
−
=
N
kN
1073
5
,
4
0
,
97
3500
)
0
,
1
(
22
6000
12
14200
12
=
⋅
+
−
⋅
−
−
=
N
kN
Plan
M
1
M
2
V
1
V
2
2.0
2.0 2.0 2.0
2.0
2.0
2.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1 2
3 4
5 6
7 8 9
10 11
12
x
0
y
0
x
0
„0”
grubość 1,0 m
A
A
V
1
= 8000 kN,
M
1
= 10000 kNm
V
2
= 5000 kN,
M
2
= 6000 kNm
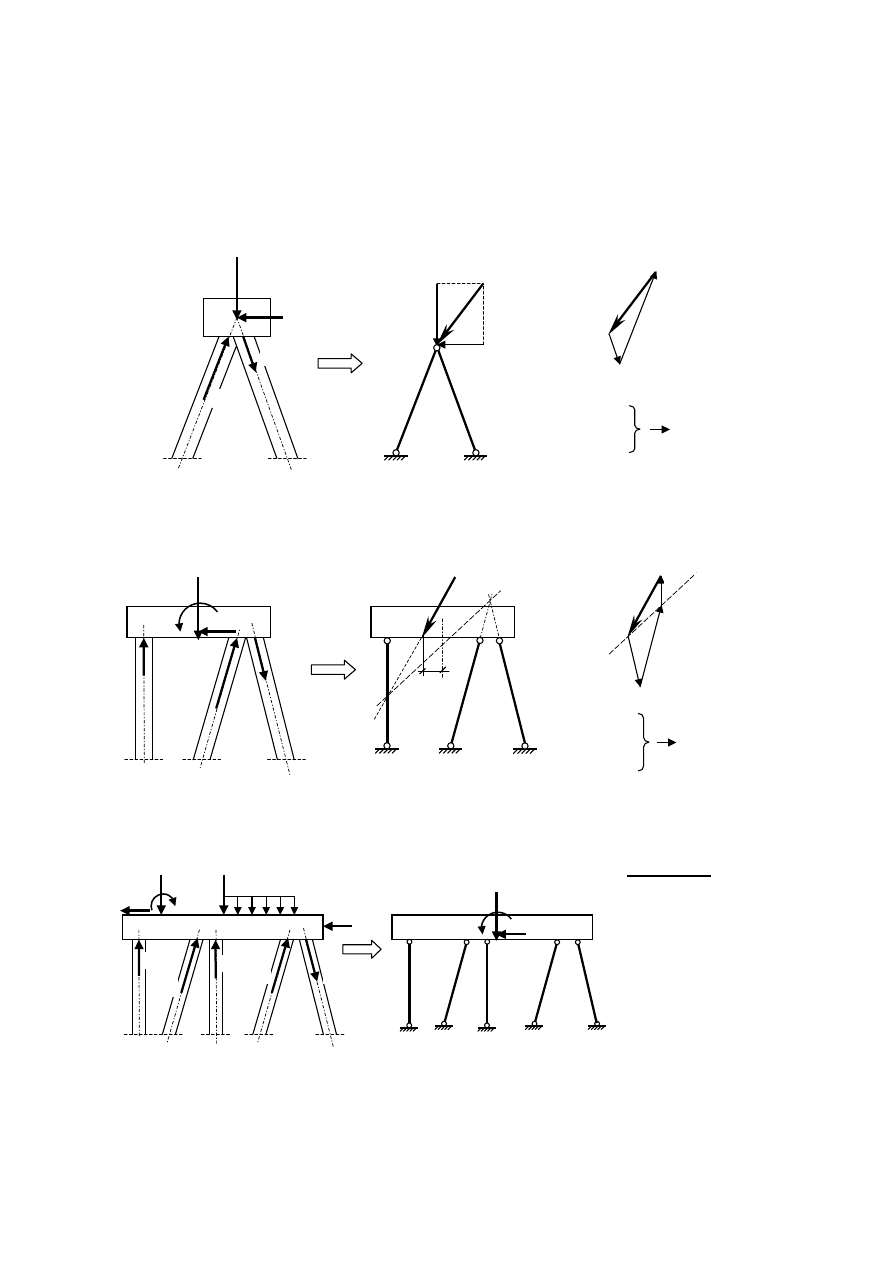
5
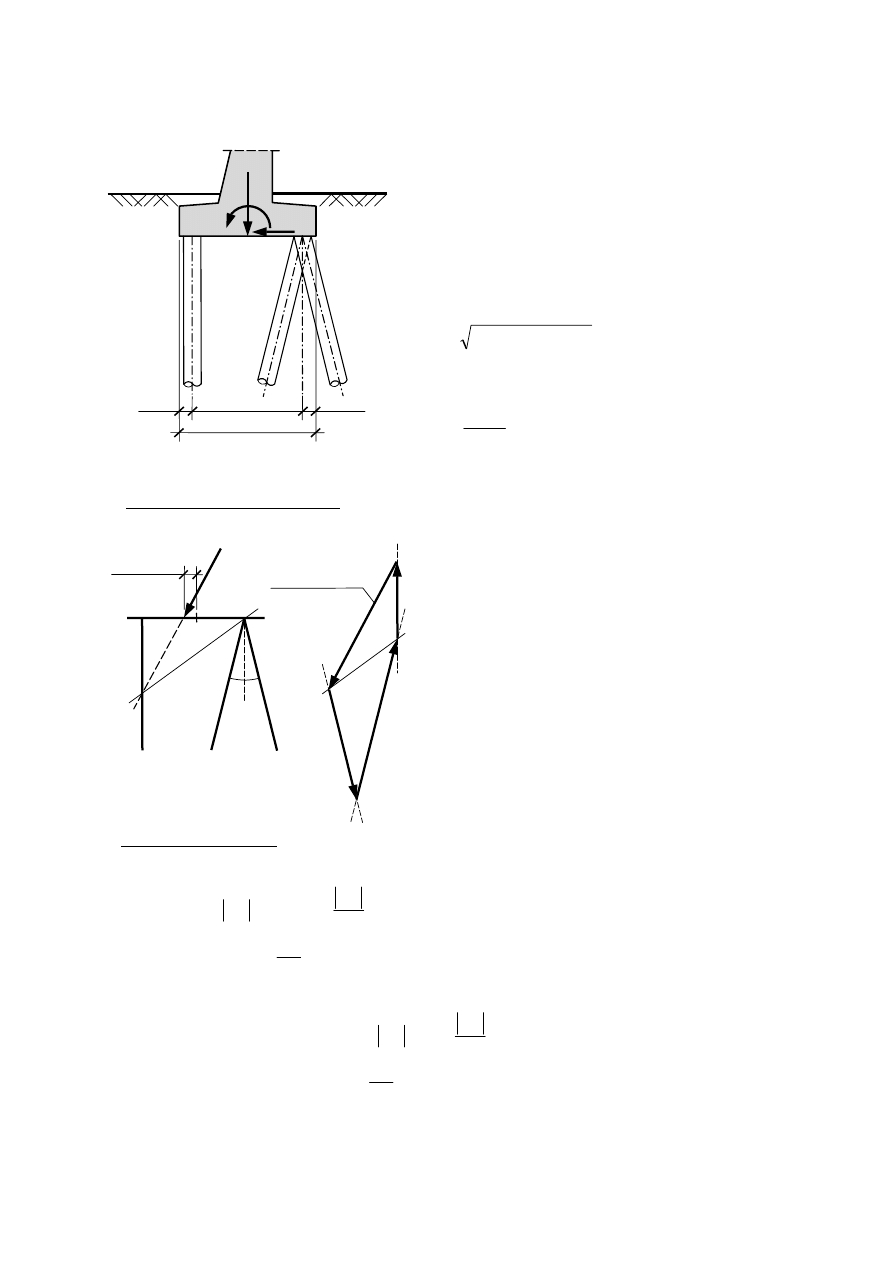
c) Układy dwuwymiarowe z palami pionowymi i ukośnymi
(np. ściany oporowe, przyczółki mostowe, nabrzeża, bloki kotwiące na palach itp.)
Układy takie stosuje się przy złożonych obciążeniach - od sił pionowych, poziomych i momentów.
Ze względu na siły poziome konieczne są pale ukośne.
– fundament na 2 palach
– fundament na 3 palach
- fundament na więcej niż 3 palach
V
H
N
1
N
2
V
H
Q
Q
N
1
N
2
rozwiązanie graficzne
Schemat
rozwiązanie analityczne:
Σ
X = 0
Σ
Y = 0
N
1
, N
2
ΣV
ΣH
N
2
N
3
Q
Q
N
1
N
2
rozwiązanie graficzne
Schemat
rozwiązanie analityczne:
Σ
X = 0
Σ
Y = 0
Σ
M = 0
N
1
, N
2
, N
3
N
1
ΣM
0
E
B
z
z
N
3
rozwiązanie :
1) w przypadku jednego pala
ukośnego możliwe rozwiązanie
analityczne
2) metoda Nökkentveda
3) metoda macierzowa
4) metoda numeryczna
np. programem komputerowym
do statyki układów prętowych
ΣV
ΣH
N
2
Schemat
N
1
ΣM
N
3
N
4
N
5
V
1
V
2
M
1
q
H
1
H
2
6
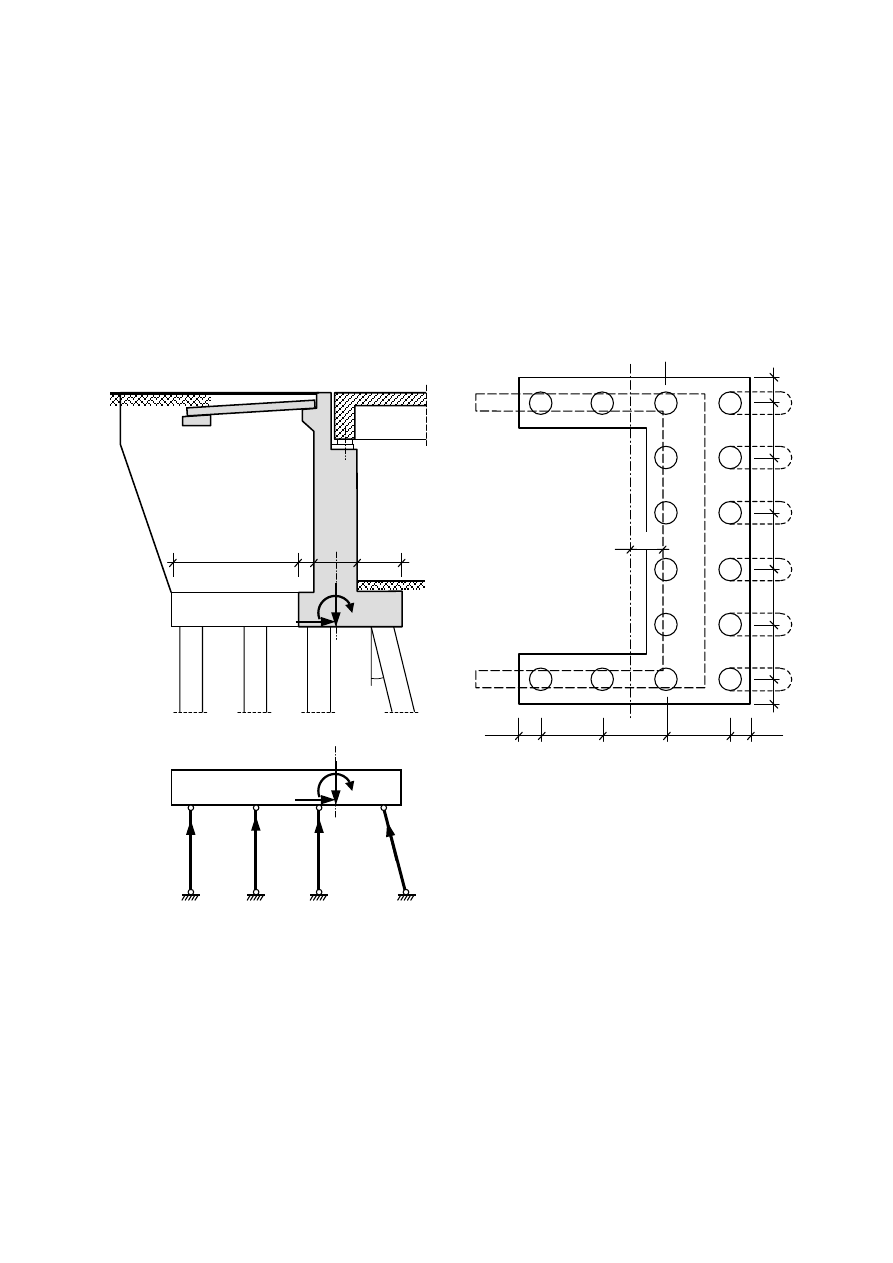
Zadanie przykładowe 4.4
Wyznaczyć metodą graficzną i analityczną wartości sił w palach pod fundamentem ściany
oporowej.
Obliczenia:
Obciążenia sprowadzone do geometrycznego środka
podstawy fundamentu:
40
,
302
=
V
kN/m
27
,
143
=
H
kN/m
7
,
81
0
=
M
kNm/m
Wypadkowa obciążeń:
6
,
334
27
,
143
4
,
302
2
2
=
+
=
Q
kN/m
Mimośród przyłożenia wypadkowej względem
geometrycznego środka płyty fundamentowej:
27
,
0
4
,
302
7
,
81
=
=
B
e
m
a) Metoda graficzna Culmanna
(skala sił 1 cm = 100 kN/m):
Odczytujemy z wieloboku sił długości wektorów S
1
,
S
2
i S
3
. Przeliczamy odczytane wielkości na
jednostki siły według przyjętej skali:
S
1
= 1,8 · 100 = 180,0 kN/m
S
2
= 3,6 · 100 = 360,0 kN/m
S
3
= 2,35 · 100 = 235,0 kN/m
W palu nr 3 jest siła wyciągająca.
b) Metoda analityczna:
Suma momentów względem punktu B:
0
)
2
(
0
1
=
+
⋅
−
⋅
→
=
Σ
AB
e
V
AB
S
M
B
k
B
=
→
=
+
⋅
−
⋅
1
1
0
)
2
5
,
2
27
,
0
(
4
,
302
5
,
2
S
S
183,9 kN/m
Suma momentów względem punktu A:
(
)
0
)
2
(
cos
cos
0
3
2
=
−
⋅
+
⋅
⋅
−
⋅
−
→
=
Σ
B
k
A
e
AB
V
AB
S
S
M
α
α
(
)
2
,
122
0
)
27
,
0
2
5
,
2
(
4
,
302
5
,
2
97
,
0
97
,
0
2
3
3
2
+
−
=
→
=
−
⋅
+
⋅
⋅
−
⋅
−
S
S
S
S
Suma rzutów sił na oś X:
0
sin
sin
3
2
=
−
⋅
−
⋅
k
H
S
S
α
α
0
27
,
143
242
,
0
242
,
0
3
2
=
−
⋅
−
⋅
S
S
H
V
M
0
0,35 m
0,35 m
2,50 m
3,20 m
(1)
(3)
(2)
z
0
A
B
(1)
α
(3)
α
(2)
Q
= 334,6 kN/m
e
B
= 0,27 m
C
S
1
S
2
S
3
z
Q = 334,6 kN
(3,35 cm)
S
2
(3,6 cm)
S
3
(2,35 cm)
S
1
(1,8 cm)
7
Podstawiamy 2
,
122
2
3
+
−
= S
S
:
(
)
=
→
=
−
⋅
+
−
−
⋅
2
2
2
0
27
,
143
242
,
0
2
,
122
242
,
0
S
S
S
357,2 kN/m
=
+
−
=
+
−
=
2
,
122
2
,
357
2
,
122
2
3
S
S
-235 kN/m
Różnice pomiędzy metodą a) i b) wynikają z niedokładności pomiarowych w metodzie a).
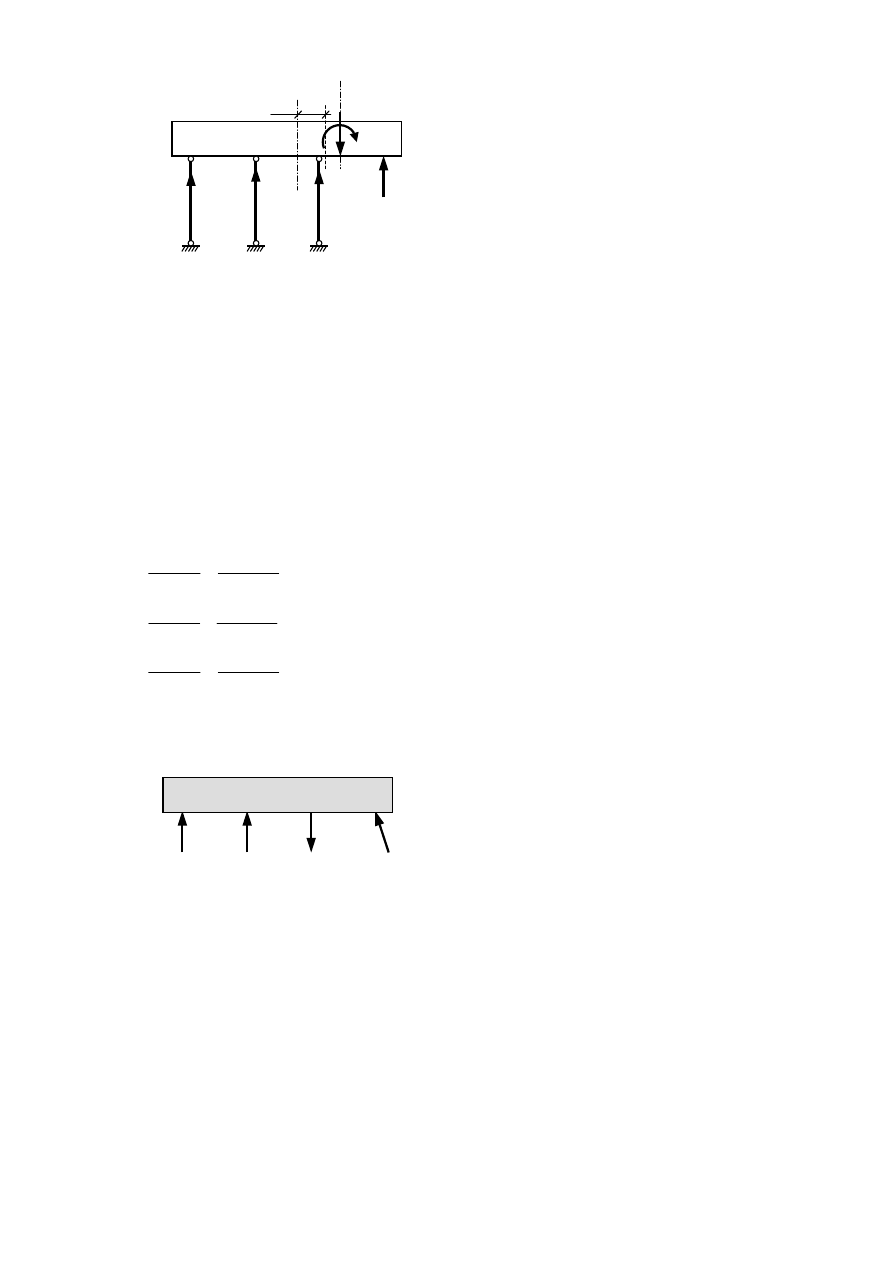
Zadanie przykładowe 4.5
Stosując metodę sztywnego oczepu policzyć siły w palach fundamentu palowego przyczółka
wiaduktu drogowego przedstawionego na rysunku. W obciążeniach uwzględniony jest również
ciężar przyczółka i oczepu fundamentowego.
Z równowagi sił poziomych wyznaczamy siłę w palach w rzędzie (1)
°
=
→
=
5
,
9
6
/
1
tan
α
α
19400
5
,
9
sin
/
3200
sin
/
0
sin
0
1
1
=
°
=
=
→
=
⋅
−
→
=
∑
α
α
H
N
N
H
X
kN
Siła w pojedynczym palu:
=
=
′
6
/
19400
1
N
3230
kN
Myślowo usuwamy pale z rzędu nr (1), a składową pionową siły N
1
traktujemy jako dodatkowe
obciążenie zewnętrzne. Usuwamy też ze schematu obciążenia poziome.
19130
5
,
9
cos
19400
cos
1
1
=
°
⋅
=
⋅
=
α
N
N
v
kN
1,5
2,0
0,5
5,0
V
M
H
2,5
2,5
2,5
0,75
0,75
Plan palowania
V = 15000 kN
H = 3200 kN
M = 4800 kNm
2,2
2,2
2,2
2,2
2,2
1,0
1,0
6:1
(4)
(1)
(2)
(3)
α
A
A
y
0
y
0
x
0
V
M
H
(4)
(2)
(3)
N
4
N
3
N
2
N
1
„0”
(1)
Schemat
8
Środek geometryczny nowego układu pali:
S
yA
= -2
⋅2,5 – 2⋅5,0 = –15,0 m
x
0
= –15,0/10 = –1,5 m
Obciążenia sprowadzone do punktu „0”:
ΣV = 15000 –19130 = –4130 kN
ΣM
y0
= 4800 + 15000
⋅(0,5 + 1,5) –19130⋅(2,5 + 1,5) = –41720 kNm
Momenty bezwładności układu pali względem osi y
0
:
Σx
i
2
= 6
⋅1,5
2
+ 2
⋅1,0
2
+ 2
⋅3,5
2
= 40,0 m
2
Siły w pozostałych palach (wartości na pojedyncze pale):
=
⋅
−
+
−
=
′
5
,
1
0
,
40
41720
10
4130
2
N
–1978 kN
→ siła wyciągająca pal
=
−
⋅
−
+
−
=
′
)
0
,
1
(
0
,
40
41720
10
4130
3
N
630 kN
=
−
⋅
−
+
−
=
′
)
5
,
3
(
0
,
40
41720
10
4130
4
N
3240 kN
V
M
N
1v
A
A
„0”
y
0
x
0
y
0
N
4
N
3
N
2
N
′
1
= 3230
N
′
2
= 1978
N
′
3
= 630
N
′
4
= 3240
(Siły w pojedynczych palach [kN])
Prezentacja wyników obliczeń
9
Metoda sprężystego oczepu na podporach sprężystych
W obliczeniach uwzględnia się rzeczywistą sztywność oczepu (np. belki, rusztu lub płyty), a pale
wyraża się w postaci podpór sprężystych o sztywnościach k
z
. Sztywności te wyznacza się z obliczeń
osiadań pali. Przy niedużej liczbie pali, sztywność k
z
można przyjąć w przybliżeniu z zalezności:
D
.
N
)
N
(
s
N
k
t
t
t
z
⋅
≈
=
01
0
[kN/m]
w którym:
N
t
– nośność pala na wciskanie obliczona według normy,
s(N
t
) – osiadanie pala przy mobilizacji nośności N
t
. Z wielu próbnych obciążeń pali wynika, że
osiadanie to wynosi w przybliżeniu 1% średnicy pala (0.01
⋅D).
W wyniku obliczeń otrzymuje się siły w palach oraz siły wewnętrzne w oczepie (momenty
zginające, siły tnące) oraz jego przemieszczenia (ugięcia). Nie otrzymuje się w tej metodzie
momentów zginających w palach. Rozwiązanie układu wykonać najlepiej za pomocą
odpowiedniego programu komputerowego do liczenia układów prętowych i płyt.
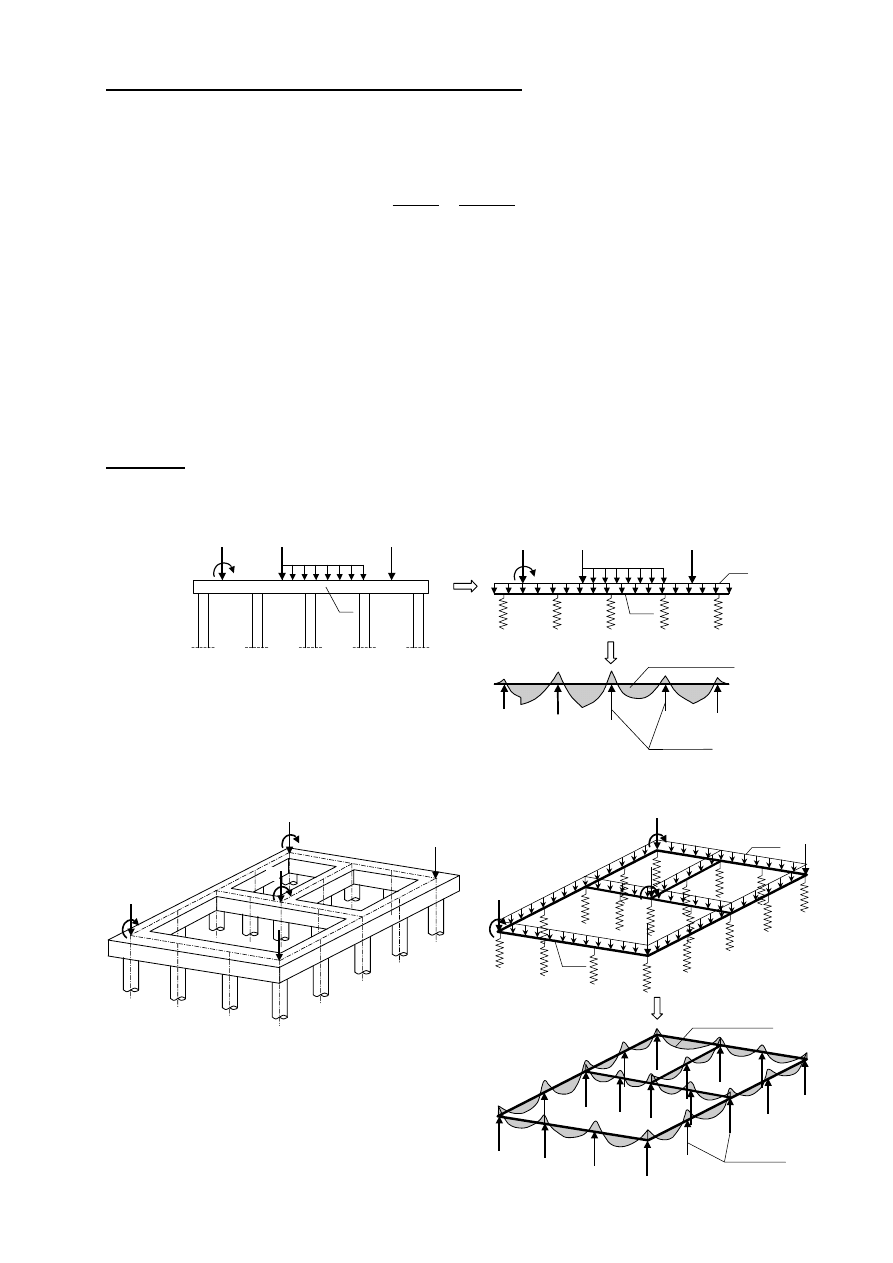
Przykłady:
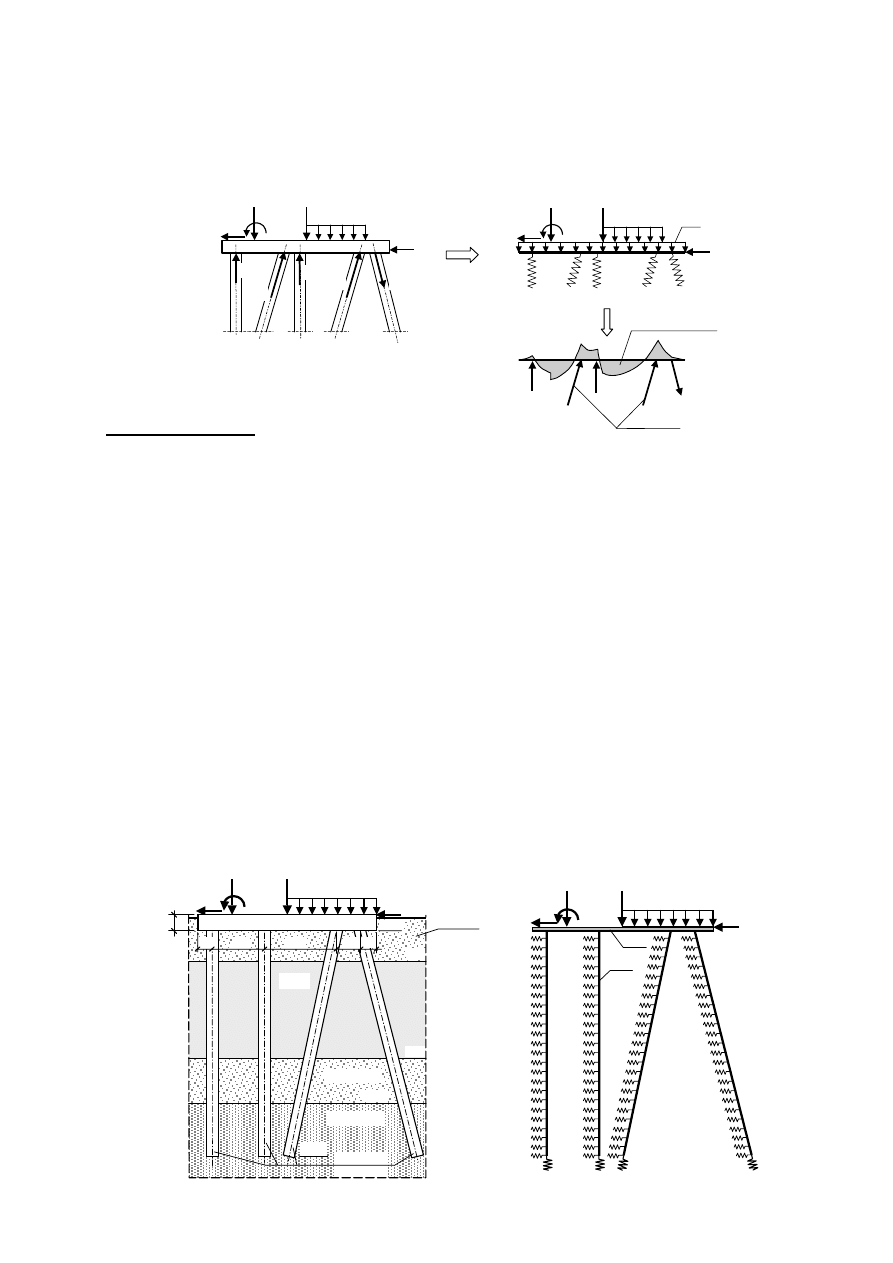
a) belka na podporach sprężystych obciążona pionowo i momentami
b) ruszt na podporach sprężystych obciążony pionowo i momentami
V
4
V
5
V
3
V
1
V
2
M
4
M
1
M
3
V
1
V
2
M
1
q
Schemat
V
3
V
1
V
2
M
1
q
V
3
g
F
EJ
F
k
z
k
z
k
z
k
z
k
z
N
1
N
2
N
3
N
4
N
5
wykres momentów
rozwiązanie
g
F
siły w palach
M
1
N
1
N
2
N
j
wykres momentów
siły w palach
k
z
V
4
V
5
V
2
V
1
V
3
q+g
F
Schemat
rozwiązanie
M
4
M
3
EJ
F
GJ
sF
EJ
F
– sztywność giętna
belek rusztu
GJ
sF
– sztywność skrętna
belek rusztu
N
i
10
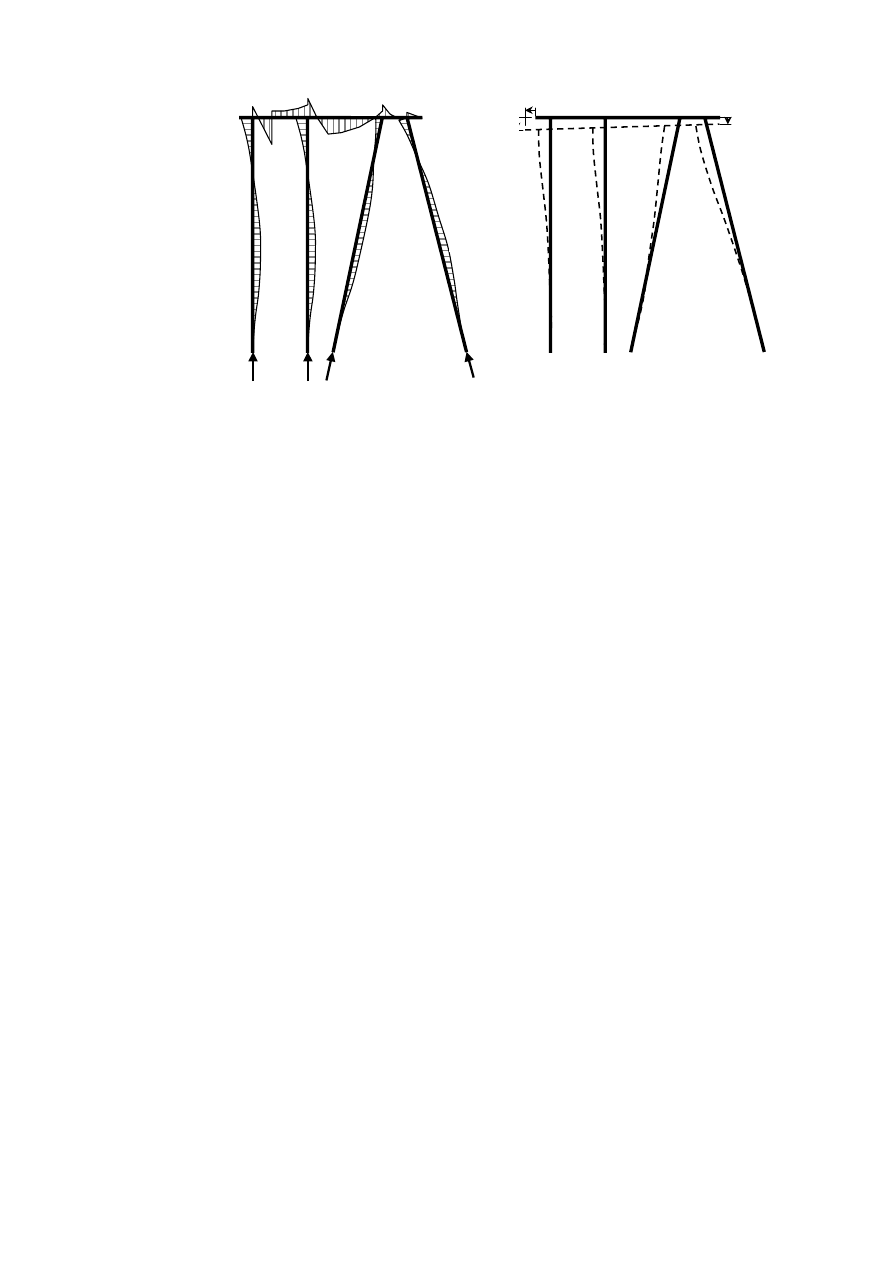
c) płyta na podporach sprężystych obciążona pionowo i momentami
Przygotowanie schematu statycznego i obliczenia podobne do rusztu belkowego na palach.
Obliczenia wykonuje się programami komputerowymi do analizy statycznej płyt (MES).
d) fundament palowy obciążony pionowo, poziomo i momentami (z palami ukośnymi)
Metoda uogólniona
W metodzie tej przygotowuje się schemat obliczeniowy fundamentu palowego, w którym pale
modeluje się w postaci prętów współpracujących na całej swojej długości z gruntem jako
ośrodkiem sprężystym lub sprężysto-plastycznym. Uwzględniony jest w ten sposób wpływ
warunków gruntowych na pracę całego układu i na otrzymywane wyniki obliczeń. Metody
sztywnego i sprężystego oczepu tego wpływu nie uwzględniją. Współpracę pali z gruntem wyraża
się za pomocą szeregu podpór sprężystych lub sprężysto-plastycznych, rozmieszczonych wzdłuż
pali. Odpowiednie dobranie parametrów tych podpór jest największą istotą metody. Sposób ich
określania w Polsce opracował M. Kosecki (1988, 2006).
Powstające w efekcie schematy statyczne fundamentów palowych są wielokrotnie statycznie
niewyznaczalne i wymagają do rozwiązania programów komputerowych do macierzowej analizy
konstrukcji. W przypadku podpór sprężystych obliczenia wykonuje się jednoetapowo,
a w przypadku podpór sprężysto-plastycznych – kilkuetapowo: iteracyjnie lub przyrostowo.
W wynikach obliczeń otrzymuje się w miarę rzeczywiste wartości sił i momentów w palach, sił
wewnętrznych w nadbudowie i przemieszczeń całej konstrukcji. Jak dotąd jest to najlepsza
z praktycznych metod obliczania fundamentów palowych, znajdująca zastosowanie w projektowa-
niu.
Przykład fundamentu palowego obliczonego metodą uogólnioną.
N
2
N
2
Schemat
N
1
N
3
N
4
N
5
V
1
V
2
M
1
q
H
1
H
2
V
1
V
2
M
1
q
H
1
H
2
k
z
g
F
rozwiązanie
k
z
k
z
k
z
k
z
N
1
N
3
N
4
N
5
wykres momentów
siły w palach
V
1
=1000 kN V
2
=800 kN
M
1
=1500
kNm
q=60 kN/m
H
1
=300 kN
H
2
=200 kN
Pd,
I
D
=0.35
0,8
1,0
3,5
5,0
1,5 1,0
T/Nm
Pd, I
D
=0.50
Pd, I
D
=0.70
-1,0
-3,0
-8,0
-10,0
-12.0
pale Vibro
φ460 mm
V
1
V
2
M
1
q
H
1
H
2
k
xi
K
z
EJ
p
EJ
F
Schemat
11
Rozwiązanie
N
1
=1088
191
169
72
79
62
60
49
49
N
2
=902
N
3
=623
N
4
=41
1316
211
184
457
712
150
50
7.0
8.0
1.0
M [kNm]
N [kN]
δ [mm]
12
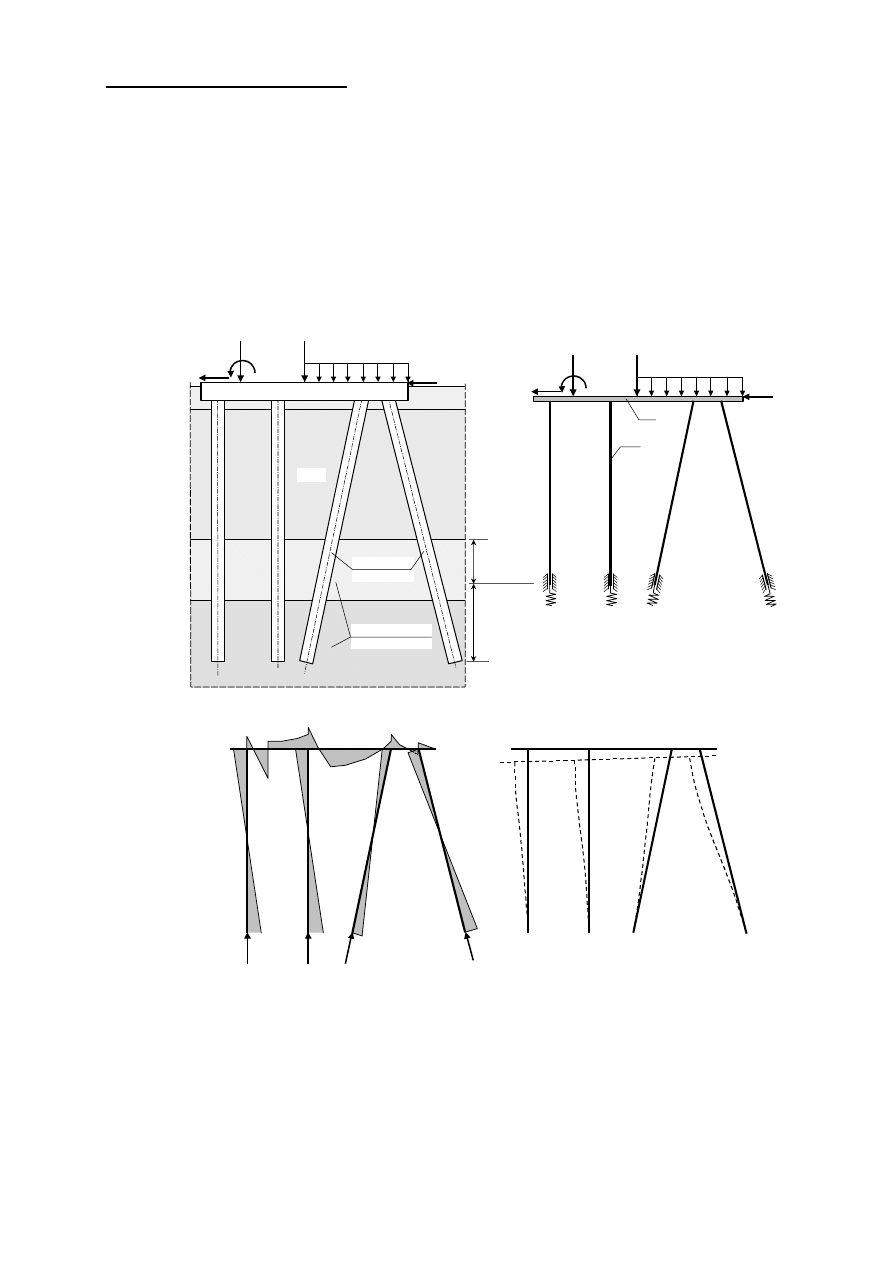
Metody obliczeniowe pośrednie
W niektórych przypadkach możliwe są uproszczenia w metodzie uogólnionej. Polegają one
np. na przyjęciu jako prętów górą połączonych sztywno z oczepem, a dołem utwierdzonych na
obrót w gruncie nośnym na pewnej głębokości (od 3 do 5 średnic pala) i sprężyście podpartych
w kierunku osiowym. Takie uproszczenie jest możliwe do zastosowania przy obliczaniu palowych
konstrukcji wodnych (np. pirsy, nabrzeża, pomosty) oraz w przypadku występowania w podłożu
gruntowym bardzo słabych warstw od samego oczepu, aż do warstw nośnych, w których zagłębione
są pale (również bez warstw wytrzymałych pomiędzy warstwami słabymi). Aby możliwe było
przyjęcie utwierdzenia pali w warstwach nośnych potrzebne jest dość znaczne ich zagłębienie
w tych warstwach, na co najmniej 6 do 10 średnic pali (patrz rysunek poniżej).
W powyższym rozwiązaniu otrzymuje się zawyżone wartości przemieszczeń poziomych
fundamentów oraz momentów zginających w palach.
V
1
V
2
M
1
q
H
1
H
2
T/Nm
V
1
V
2
M
1
q
H
1
H
2
K
z
EJ
p
EJ
F
warstwy gruntów
nośnych
∼(3÷5)D
≥(3÷5)D
pale
o średnicy D
poziom utwier-
dzenia pali
Schemat
N
1
N
2
N
3
N
4
[ M, N ]
[ δ ]
Rozwiązanie