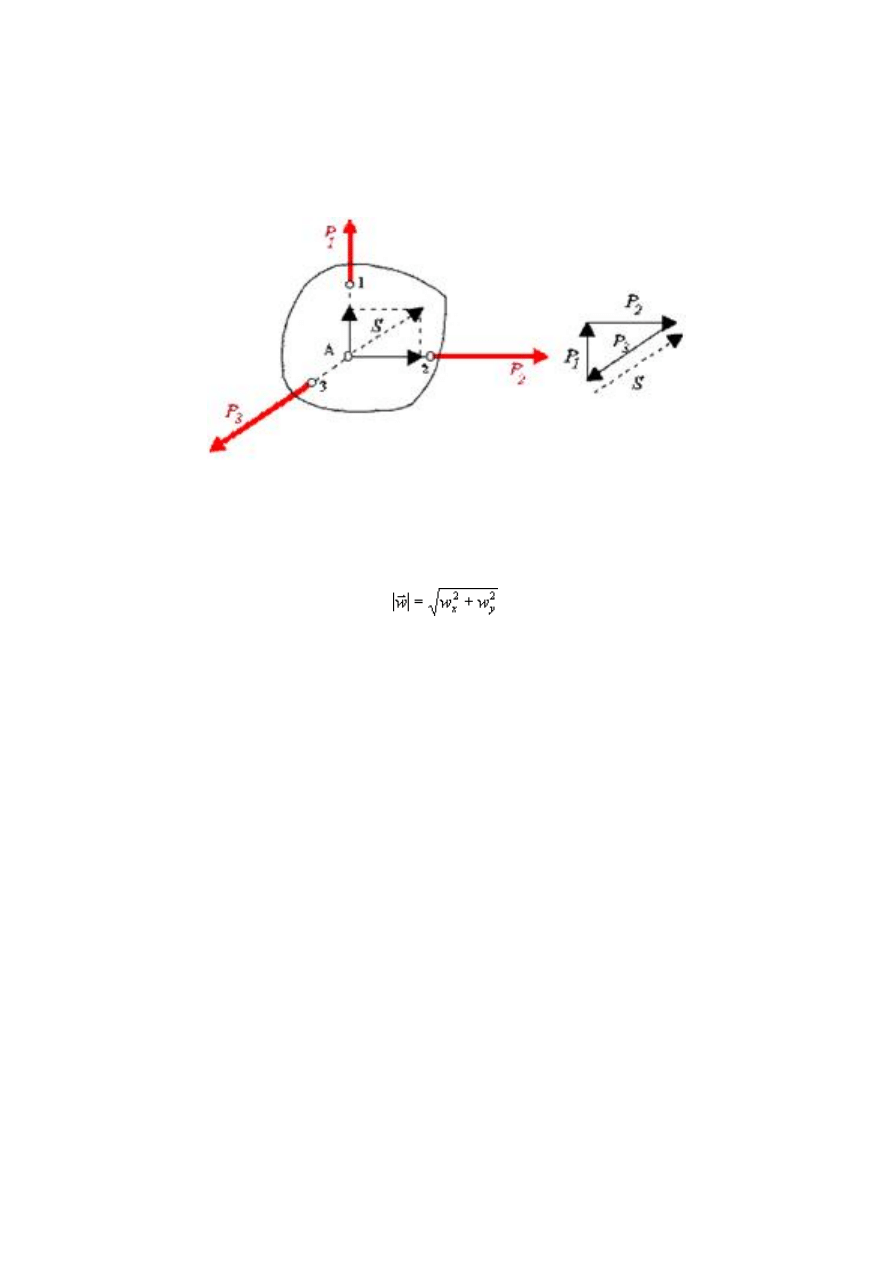
Wyznaczanie wektora sumy sił metodą analityczną

Wyznaczenie wektora wypadkowego w sytuacji działania wielu sił polega na
wykorzystaniu twierdzenia Pitagorasa:

Rys.1 Rozkład sił na składowe

Dzięki możliwości rozłożenia sił w Kartezjańskim układzie współrzędnych można
wyprowadzić wzór na długość wektora:

Wyznaczanie wektora sumy sił możliwe jest dzięki zastosowaniu wzoru:

Żeby dodać dwa wektory metodą analityczną, gdy znamy ich współrzędne, należy

dodać odpowiednie współrzędne - x-owe do x-owych, a y-owe do y-owych (ew. z-

owe do z-owych).

(w

x

, w

y

) + (u

x

, u

y

) = (w

x

+u

x

, w

y

+u

y

)

Moment siły względem punktu.

Moment M

A

siły P względem punktu A jest to iloczyn M

A

=Ph

Mierzymy go w niutonometrach [Nm], gdzie h jest to najkrótszą odległością punktu
A od prostej, na której leży wektor siły P, patrz rysunek nr 2.

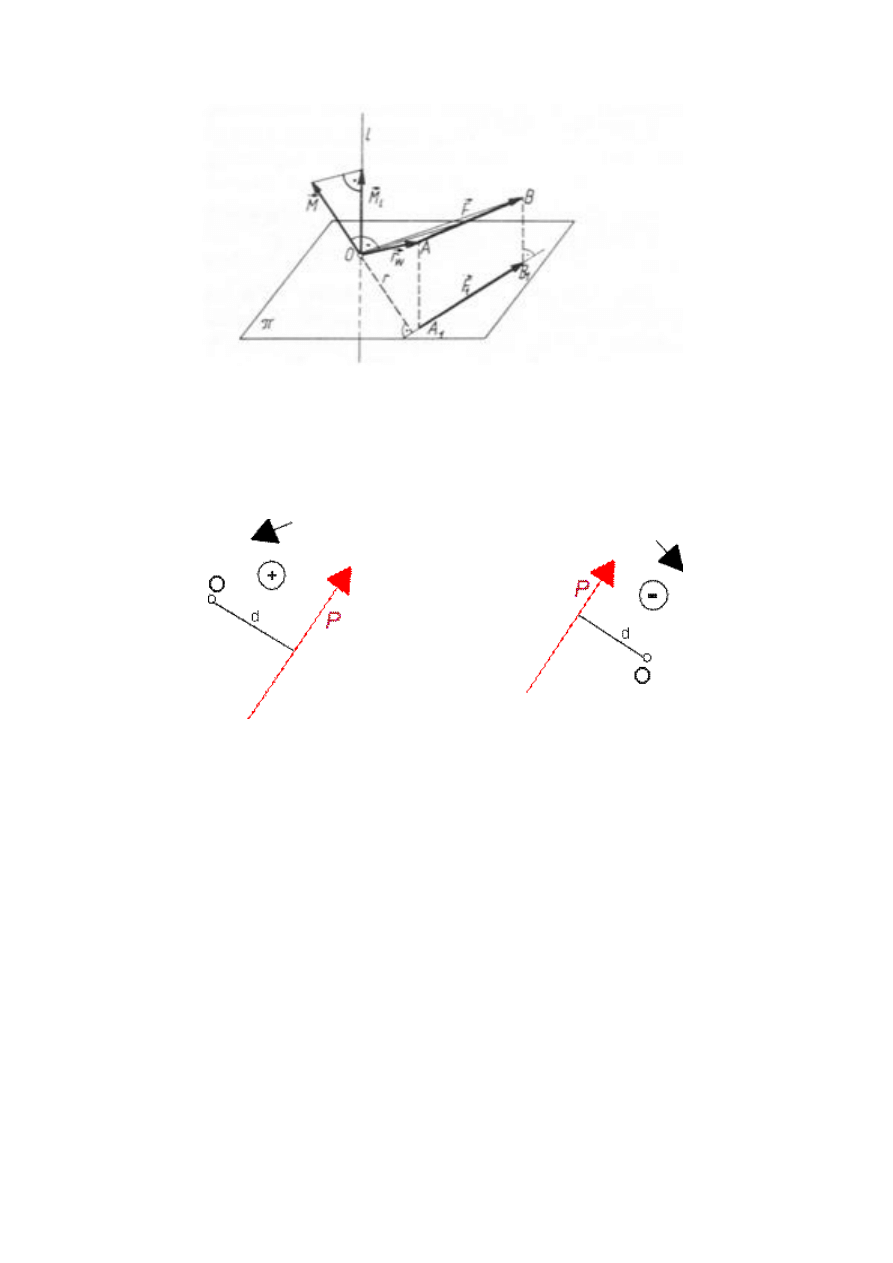
Rys. 2. Wektor momentu siły względem punktu

Odległość h nazywamy ramieniem, na którym siła P wywołuje moment M

A

.

Moment M

A

może mieć znak (+) lub (-).

Aby ustalić znak przeanalizujmy rysunek nr 3.

Rys. 3. Sposób określania znaku momentu

Postępowanie w przypadku redukcji sił do zadanego punktu:

Redukcja sił do zadanego punktu polega na przesuwaniu równoległym tych sił tak
aby ich kierunki przecinały się w jednym punkcie. Następnie wykorzystuje się
możliwość przesuwania wektora wzdłuż linii kierunkowej. W ten sposób tworzony
jest układ zbieżny, który może być rozwiązany za pomocą poznanych wcześniej
metod.

Warunki równowagi dla płaskiego układu sił:

Płaski

dowolny

układ

sił

jest

w

równowadze,

jeżeli

są

równocześnie

spełnione

dwa

warunki:

1.

Algebraiczne

sumy

rzutów

wszystkich

sił

układu

na

dwie

osie

prostokątnego

układu

odniesienia

są

równe

zero.

2.

Moment

główny

układu

względem

dowolnie

obranego

bieguna na płaszczyźnie działania sił jest równy zero.

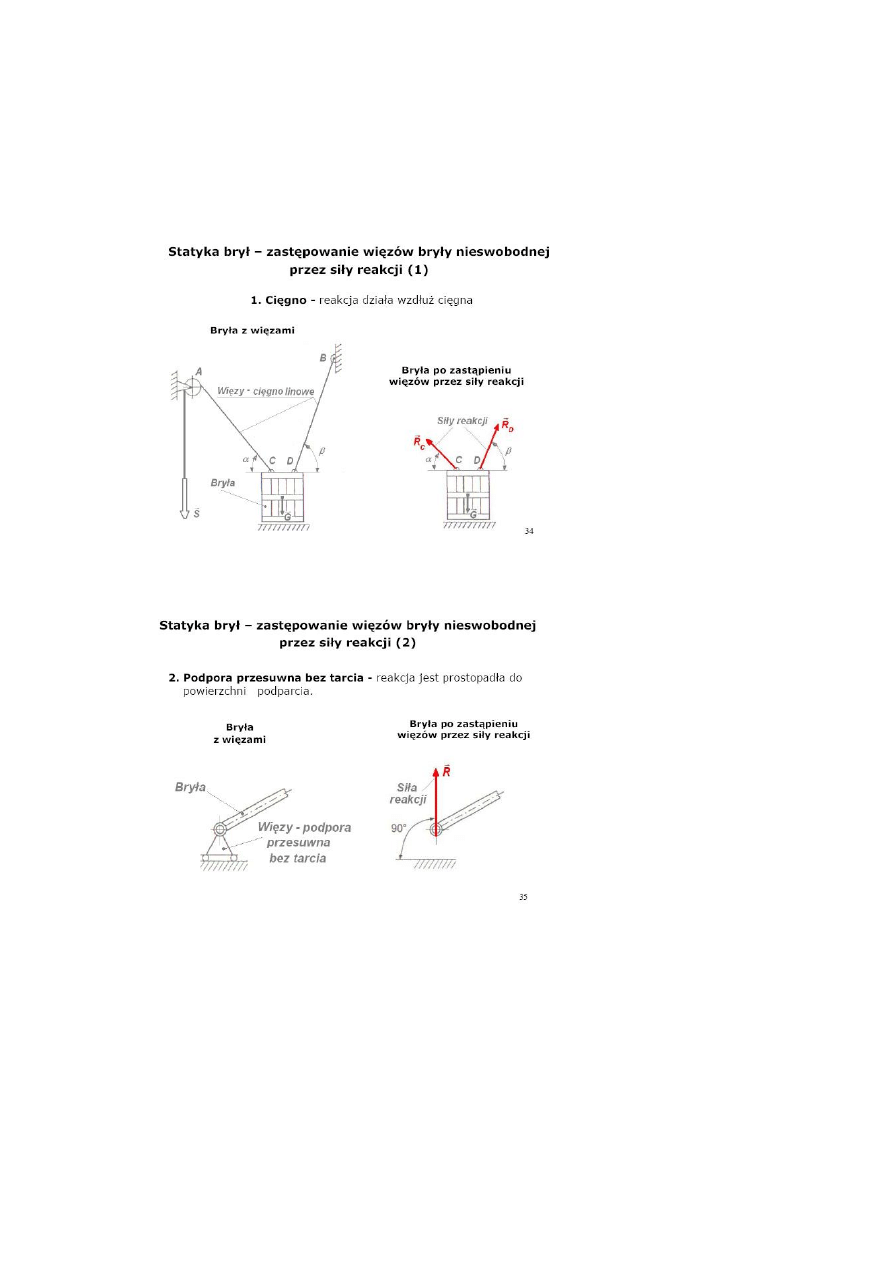
Rodzaje więzów (podpór) oraz rozkład ich sił:

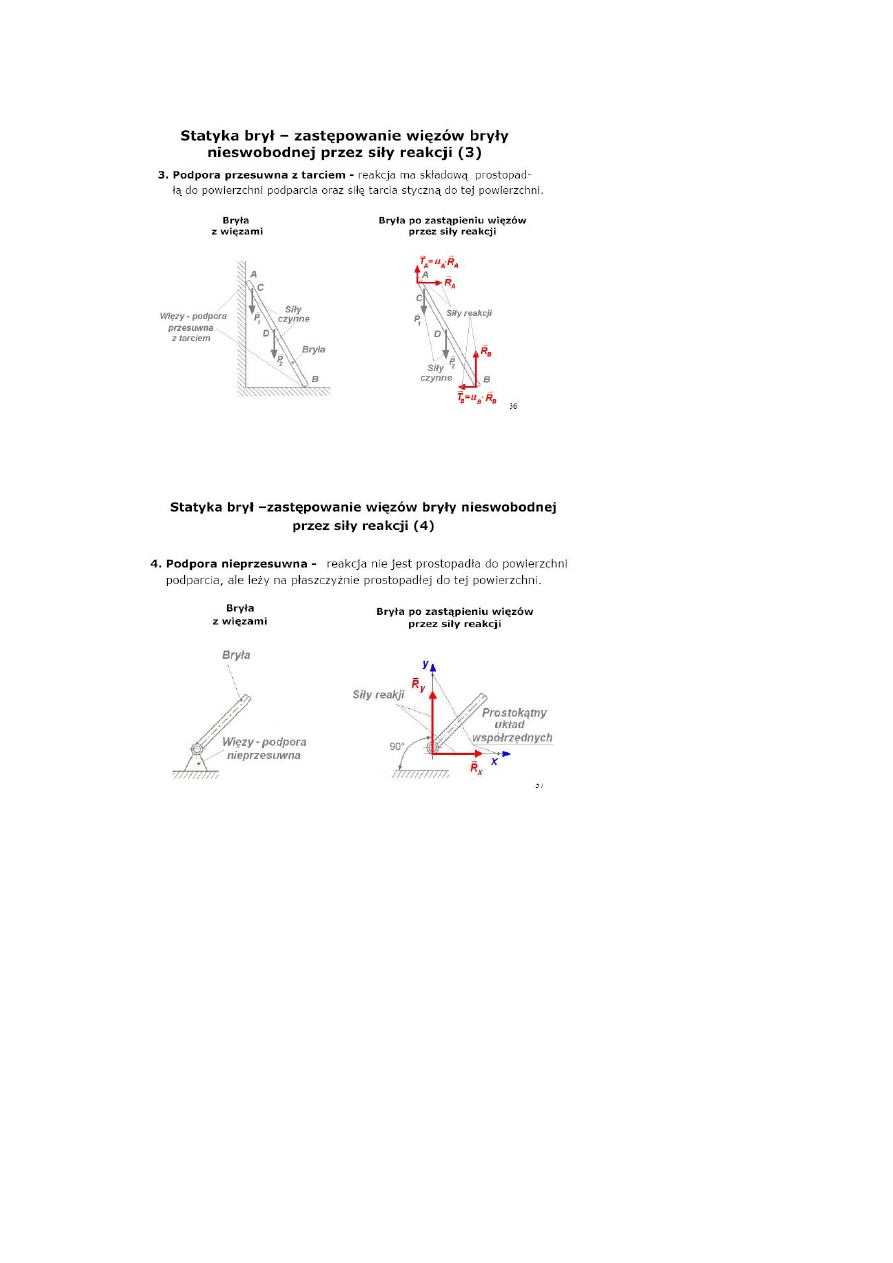
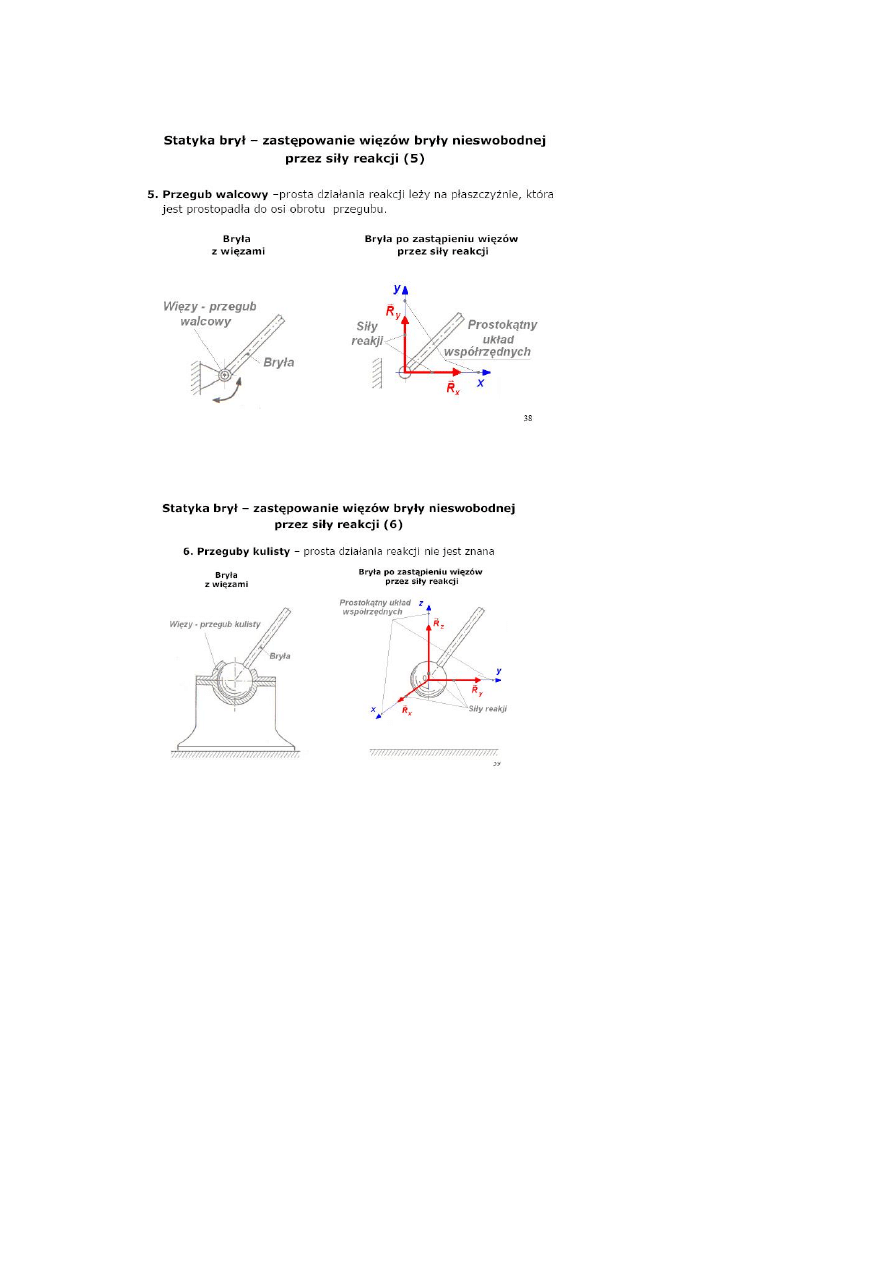
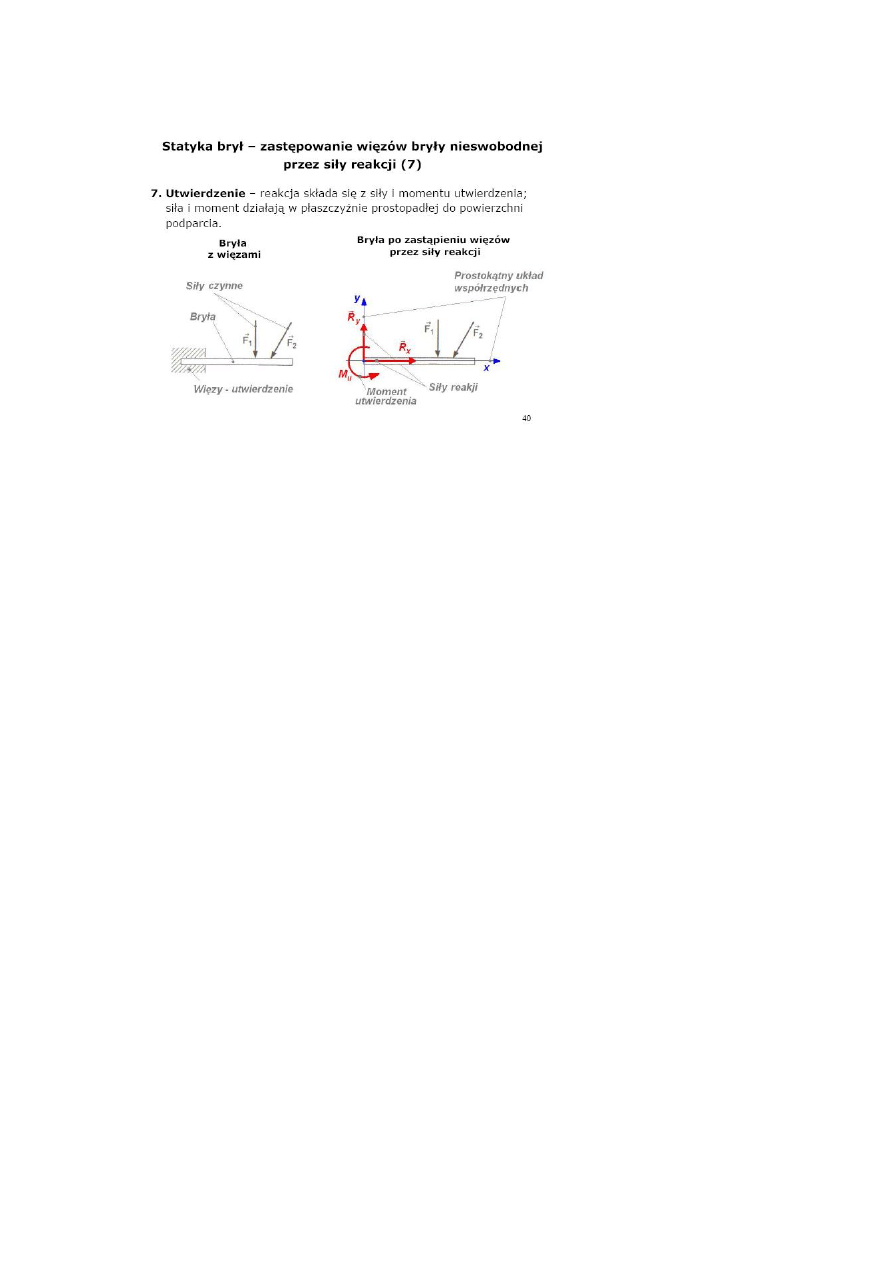
Układ sił jest w równowadze jeśli wypadkowa sił jest równa zero.