2013-01-12

1

CHEMIA

CHEMIA

CIAŁA STAŁEGO

CIAŁA STAŁEGO

WŁAŚCIWOŚCI MAGNETYCZNE CIAŁ STAŁYCH

Zaawansowane materiały i nanotechnologia

Zaawansowane materiały i nanotechnologia

Uniwersytet Jagiello

Uniwersytet Jagiellońński

ski

dr hab. Krzysztof Kruczała

konsultacje: środa 11:30-12:30, pokój 139

Wszystkie ciała ulegają działaniu pola magnetycznego.

Różnice w ich zachowaniu w polu magnetycznym
stanowią podstawę klasyfikacji na:

- diamagnetyki,

- paramagnetyki,

- ferromagnetyki,

- ferrimagnetyki,

- antyferromagnetyki.

Klasyfikacja ciał stałych

ze względu na właściwości magnetyczne

Diamagnetyki

(zamknięte powłoki elektronowe - brak trwałego momentu

magnetycznego, indukowany moment magnetyczny przeciwny do kierunku
zewnętrznego pola).

Paramagnetyki

(niesparowane elektrony – trwały moment magnetyczny).

Ferro-, antyferro- i ferrimagnetyki

(trwałe, uporządkowane momenty

magnetyczne).
Diamagnetyzm związany z obecnością zamkniętych powłok elektronowych
(sparowane elektrony) jest powszechną właściwością materii. Niektóre
substancje mają ponadto niesparowane elektrony, powodujące
występowanie trwałego momentu magnetycznego. Momenty magnetyczne
mogą być zorientowane przypadkowo i wówczas substancja jest
paramagnetyczna.
W przypadku uporządkowania trwałych momentów w obrębie płaszczyzn
krystalograficznych występuje ferro-, antyferro- lub ferrimagnetyzm.

paramagnetyki

ferromagnetyki

ferrimagnetyki

antyferromagnetyki

Klasyfikacja ciał stałych

ze względu na właściwości magnetyczne

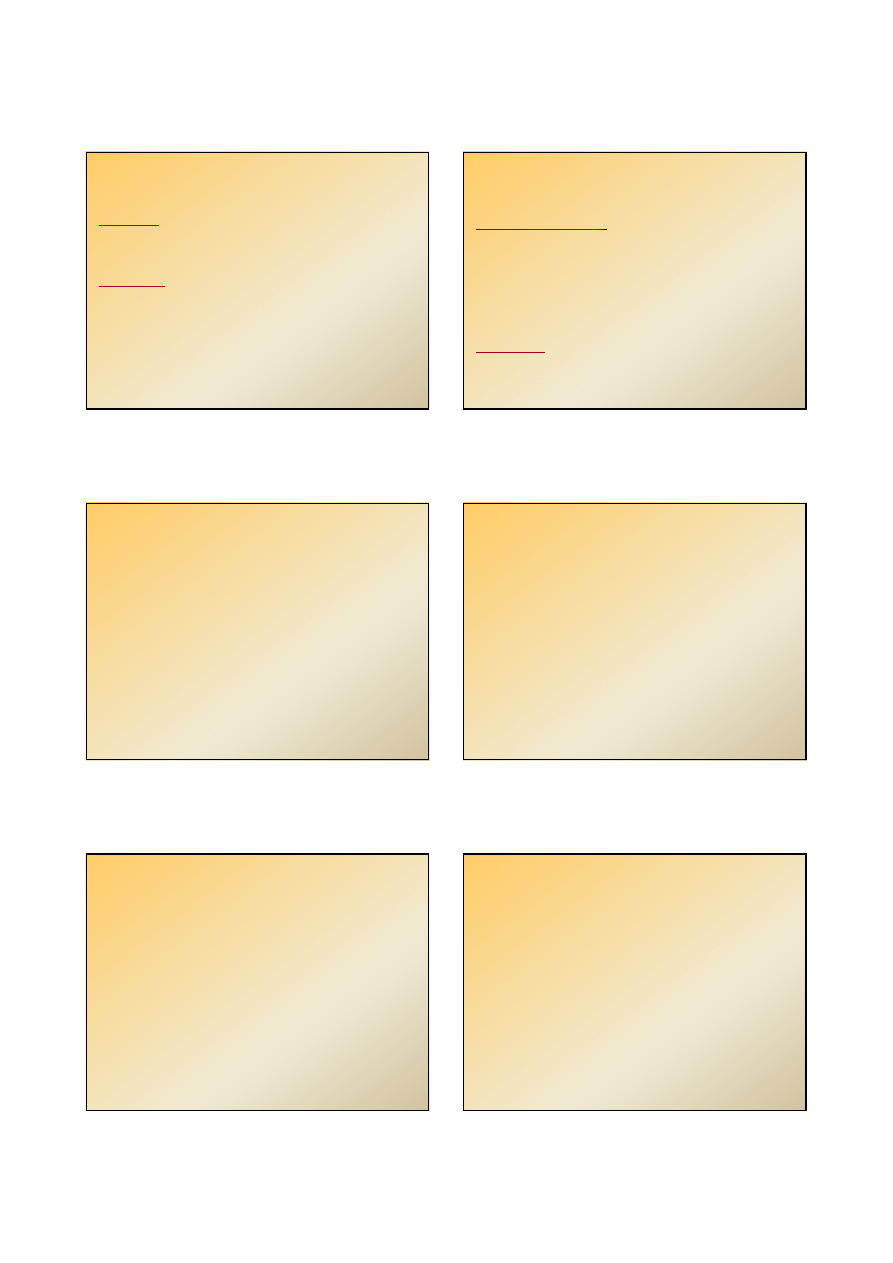
B – indukcja magnetyczna

,

tj. gęstość linii sił pola magnetycznego

Gęstość linii sił pola

w substancjach

diamagnetycznych

znajdujących się

w jednorodnym polu magnetycznym
jest

mniejsza niż w próżni

.

W paramagnetykach, ferro- i ferri-
magnetykach

umieszczonych

w zewnętrznym jednorodnym polu
magnetycznym

gęstość linii sił pola

jest

większa

niż w próżni.

B < B

vac

diamagnetyki

B = B

vac

B > B

vac

paramagnetyki
ferromagnetyki

Jednorodne pole magnetyczne

elektromagnes

pró bka

b

c

a

waga Gouy’a

diamagnetyki

paramagnetyki
ferromagnetyki

Diamagnetyki

są

wypychane

z niejednorodnego pola magnetycznego.

Paramagnetyki

są

wciągane

, a

ferromagnetyki silnie wciągane

w

niejednorodne pole magnetyczne.

Niejednorodne pole magnetyczne

Gdy substancja zostaje umieszczona w jednorodnym polu

magnetycznym H, gęstość linii sił pola w próbce (

indukcja

magnetyczna, B

) jest dana przez sumę H i członu 4

l, związanego z

samą próbką:

B = H + 4

l

gdzie

l

jest

momentem magnetycznym

próbki na jednostkę objętości.

Przenikalność magnetyczna P

i

podatność



są definiowane

równaniami:

P = B/H = 1 + 4



 = l /H

Podatność molowa



jest dana równaniem:

 = M/d

gdzie

M

jest masą mola, a

d

gęstością próbki.

Definicje…

2013-01-12

2

Alfabet grecki

Gdy substancja zostaje umieszczona w jednorodnym polu

magnetycznym H, gęstość linii sił pola w próbce (

indukcja

magnetyczna, B

) jest dana przez sumę H i członu 4

l, związanego z

samą próbką:

B = H + 4

l

gdzie

l

jest

momentem magnetycznym

próbki na jednostkę objętości.

Przenikalność magnetyczna P

i

podatność



są definiowane

równaniami:

P = B/H = 1 + 4



 = l /H

Podatność molowa



jest dana równaniem:

 = M/d

gdzie

M

jest masą mola, a

d

gęstością próbki.

Definicje…

ciało stałe



P

diamagnetyki
paramagnetyki
ferromagnetyki
antyferromagnetyki

-1

 10

-6

P<1

0 - 10

-2

P>1

10

-2

– 10

6

P>>1

0 – 10

-2

P>1

diamagnetyki -

P < 1

, a



i



małe i ujemne

paramagnetyki -

P > 1

, a



i



są dodatnie

Po umieszczeniu w jednorodnym polu magnetycznym liczba linii sił
przechodząca przez próbkę jest większa niż w próżni dla
paramagnetyków, a mniejsza dla diamagnetyków.
W konsekwencji

paramagnetyki są wciągane w pole magnetyczne

, a

diamagnetyki wypychane z pola

.

ferromagnetyki -

P >> 1

i obserwuje się duże wartości



i



.

Substancje te są silnie wciągane w pole magnetyczne. W
substancjach antyferromagnetycznych

P > 1

, a



i



są dodatnie.

Wartości



i



są porównywalne lub nieco mniejsze niż dla

paramagnetyków.

T

C

T

N

temperatura



Para-, ferro-

i antyferro-magnetyki

Ferromagnetyki

wykazują bardzo wysoką podatność magnetyczną

w niskich temperaturach, która spada coraz to szybciej w miarę
wzrostu temperatury. Powyżej temperatury zwanej temperaturą
Curie (T

C

) zachodzi przejście

ferromagnetyzm → paramagnetyzm

Antyferromagnetyki

wykazują wzrost



ze wzrostem temperatury

aż do krytycznej temperatury zwanej temperaturą Nėela. Powyżej
T

N

antyferromagnetyk wykazuje własności paramagnetyczne.

Zależność temperaturowa

pa

ra

m

ag

ne

ty

ki

an

ty

fe

rro

m

ag

ne

ty

ki

fer

ro

ma

gn

ety

ki

 = C/(T - )

1/



prawo Curie-Weissa

Prawo Curie i Curie – Weissa

Wiele paramagnetyków spełnia
prawo Curie, szczególnie w
wysokich temperaturach:

 = C/T

gdzie C jest stałą Curie.

Często lepszą zgodność z danymi
doświadczalnymi daje prawo Curie –
Weissa:

 = C/(T - θ)

gdzie θ jest stałą Weissa.

T

- θ

θ

Dla substancji ferro- i antyferromagnetycznych zależność
temperaturowa

 spełnia prawa Curie – Weissa dla T>T

c

lub T>T

N

W

paramagnetykach

są obecne niesparowane elektrony, których

momenty w zewnętrznym polu magnetycznym wykazują tendencję do
uporządkowanej orientacji.
W

ferromagnetykach

dipole magnetyczne ustawiają się równolegle już pod

nieobecność pola, dzięki kooperatywnym oddziaływaniom
pomiędzy spinami sąsiednich jonów w sieci krystalicznej.
Duże wartości

 odzwierciedlają tu równoległe

ustawienie dużej liczby spinów. Na ogół nie wszystkie spiny są równoległe
chyba, że zastosujemy bardzo wysokie pole magnetyczne i niskie
temperatury.
W

antyferromagnetykach

momenty magnetyczne są ustawione

antyrównolegle i znoszą się wzajemnie, stąd małe wartości

.

Resztkowe wartości

 są związane z zaburzeniami w

antyrównoległym ułożeniu spinów.

Dla wszystkich materiałów efekt rosnącej temperatury polega na

wzroście energii termicznej jonów i elektronów, prowadzącym do wzrostu
nieporządku strukturalnego, co osłabia efekt pola magnetycznego. Stąd dla
paramagnetyków

 zmniejsza się ze wzrostem temperatury zgodnie z

prawem Curie lub Curie – Weissa.

Dla ferro- i antyferromagnetyków wzrost temperatury wnosi

nieporządek do perfekcyjnego uporządkowania spinów. Dla
ferromagnetyków powoduje to gwałtowny spadek

 z rosnącą temperaturą.

W przypadku antyferromagnetyków następuje wzrost

 z temperaturą.

2013-01-12

3

Diamagnetyki.

Są to ciała stałe, w których wszystkie elektrony są

sparowane. Pod nieobecność zewnętrznego pola magnetycznego
diamagnetyki nie wykazują obecności trwałych dipoli magnetycznych.
W polu magnetycznym są w nich indukowane słabe dipole magnetyczne
skierowane przeciwnie w stosunku do zewnętrznego pola.

Paramagnetyki.

Są to ciała stałe wykazujące obecność niesparowanych

elektronów, z którymi związany jest trwały moment magnetyczny. Pod
nieobecność zewnętrznego pola magnetycznego dipole są skierowane
przypadkowo. W obecności pola magnetycznego występuje tendencja do
ustawiania się dipoli zgodnie z kierunkiem tego pola. Uporządkowanie na ogół
nie jest całkowite z powodu ruchów termicznych atomów. Stąd podatność
magnetyczna

, która jest dodatnia, zależy od temperatury zgodnie z prawem

Curie:

 = C/T

lub prawem Curie-Weissa:

 = C/(T- θ)

Podsumowanie właściwości

magnetycznych

Ferro-

i

antyferromagnetyki

.

W

tym

typie

magnetyków

występują

oddziaływania

pomiędzy

dipolowymi

momentami

magnetycznymi,

prowadzące

do

równoległego

lub

antyrównoległego

uporządkowania

dalekiego zasięgu. W pierwszym przypadku prowadzi to do wytworzenia
silnego wewnętrznego pola magnetycznego.
Powyżej temperatury Curie ferromagnetyki przechodzą w paramagnetyki –
energia termiczna jest większa od energii oddziaływań magnetycznych,
powodując zburzenie uporządkowania dipoli. Przejście jest odwracalne –
obniżenie temperatury poniżej T

C

przywraca uporządkowanie.

Dla

pewnych

substancji

korzystne

jest

uporządkowanie

antyferromagnetyczne. Powyżej temperatury Néela uporządkowanie zanika i
następuje przejście do paramagnetyzmu.

Ferrimagnetyzm

występuje, gdy obecne są dwa rodzaje dipoli magnetycznych

o różnej wielkości. Ich antyferromagnetycznemu uporządkowaniu towarzyszą
właściwości ferromagnetyczne.

Podsumowanie właściwości

magnetycznych

Własności magnetyczne są często wyrażane w terminach momentu
magnetycznego μ, ponieważ jest to parametr, który może być
związany bezpośrednio z liczbą niesparowanych elektronów.
Zależność między

 a μ wyraża się wzorem:

 = N μ

2

μ

B

2

/3kT

gdzie N jest liczbą Avogadro, μ

B

magnetonem Bohra, k stałą

Boltzmanna, a T temperaturą w skali Kelvina.
Po podstawieniu wartości liczbowych na N i k otrzymujemy:

μ = 2,83 (

 T)

½

μ

B

Podatność magnetyczna i moment magnetyczny, są często
wyznaczane przy pomocy wagi Gouy’a - w przypadku
paramagnetyków próbka jest wciągana w pole magnetyczne, co
objawia się pozornym wzrostem masy próbki po włączeniu pola.
Zmierzona podatność jest korygowana na różne czynniki, m. in. na
diamagnetyzm próbki i rurki na próbkę.

Moment magnetyczny

W skali atomowej źródłem magnetyzmu są niesparowane elektrony.

Właściwości magnetyczne niesparowanych elektronów pochodzą od spinu
elektronowego kwantowanego liczbą kwantową

s

i od momentu orbitalnego

kwantowanego liczbą kwantową

l

. Jednostką momentu magnetycznego jest

magneton Bohra:

μ

B

= BM = β = eh/4πmc = 9,27 x 10

-24

JT

-1

Składowa spinowa momentu magnetycznego pojedynczego elektronu wynosi:

μ

s

= g

s

[s(s+1)]

½

μ

B

gdzie g

s

= 2,0023 jest czynnikiem rozszczepienia spektroskopowego

swobodnego elektronu, a s = ½, co daje wartość momentu spinowego dla
pojedynczego elektronu równą μ

s

= 1,73 μ

B

.

Dla atomów i jonów zawierających więcej niż 1 niesparowany elektron,

całkowity moment spinowy wynosi:

μ

S

= g

S

[S(S+1)]

½

μ

B

gdzie S jest sumą spinowych liczb kwantowych poszczególnych
niesparowanych elektronów np. dla wysokospinowego jonu Fe

3+

, o 5

elektronach 3d, S = 5/2 i μ

S

= 5,92 μ

B

.

Ź

ródła magnetyzmu

Moment orbitalny związany jest w klasycznym ujęciu z ruchem elektronu
wokół jądra. Składowa orbitalna momentu magnetycznego pojedynczego
elektronu, opisywanego orbitalną liczbą kwantową l, wynosi:

μ

l

= g

l

[l(l+1)]

½

μ

B

Dla atomów i jonów zawierających więcej niż 1 niesparowany elektron,
całkowity moment orbitalny wynosi:

μ

L

= g

L

[L(L+1)]

½

μ

B

gdzie L jest sumą orbitalnych liczb kwantowych poszczególnych
niesparowanych elektronów, a g

l

= 1.

Spinowe i orbitalne składowe momentów magnetycznych ulegają
sprzężeniu według

mechanizmu Russela-Saundersa

, dając momenty

wypadkowe kwantowane liczbami kwantowymi L i S:

μ

(S+L)

= [4S(S+1) + L(L+1)]

½

μ

B

Wieloelektronowe liczby kwantowe L i S ulegają dalszemu sprzężeniu dając
całkowitą liczbę kwantową J i odpowiedni moment magnetyczny:

μ

J

= g

J

[J(J+1)]

½

μ

B

gdzie g

J

jest współczynnikiem Landego danym równaniem:

g

J

= 1 + [J(J+1)- L(L+1) + S(S+1)]/2J(J+1)

Ź

ródła magnetyzmu

Powyższe równania stosują się do wolnych atomów lub jonów.

Na ogół nie stosują się one do ciał stałych, gdyż orbitalny moment
magnetyczny jest w nich całkowicie lub częściowo zamrożony.

Efekt ten występuje szczególnie w przypadku, gdy pole elektryczne
otaczających atomów lub jonów ma niską symetrię, co może ograniczyć
orbitalny ruch elektronów.

Momenty magnetyczne obserwowane doświadczalnie są więc bardzo często
bliskie momentom ,,tylko spinowym” (spin only, s.o.).

Czynnik rozszczepienia spektroskopowego wynosi wówczas 2:

g

S

= 1 + [S(S+1) + S(S+1)]/2S(S+1) = 2, a

μ

s.o.

= g

S

[S(S+1)]

½

μ

B

, lub

μ

s.o.

= [n(n+2)]

½

μ

B

,

gdzie n – liczba niesparowanych elektronów.

Często występują dwa stany spinowe: „wysoko spinowy” i „nisko spinowy”.

Ź

ródła magnetyzmu

2013-01-12

4

Jon

Liczba

niesparowanych 

elektronów

μ

S (obliczone)

μ

S+L(obliczone)

μ

zmierzone

V

4+

1

1,73

3,00

1,8

V

3+

2

2,83

4,47

2,8

Cr

3+

3

3,87

5,20

3,8

Mn

2+

5

5,92

5,92

5,9

Cu

2+

1

1,73

3,00

1,7

Momenty magnetyczne / μ

B

Paramagnetyczne kompleksy

metali przejściowych

●

Metoda wagi Gouy`a pozwala na wyznaczenie zależności

 = f(T).

● Ze wzoru: μ = 2,83 (

 T)

½

μ

B

możemy obliczyć efektywny moment

magnetyczny.

● Z zależności:

μ

s.o.

= g

S

[S(S+1)]

½

μ

B

, lub

μ

s.o.

= [n(n+2)]

½

μ

B

obliczamy liczbę niesparowanych elektronów w atomie przy założeniu,
że jest to moment „tylko spinowy”.

Podstawy - Hans A. Betheg (1929) i John H. Van Vleck (1932).

- wiązanie pomiędzy centralnym kationem metalu przejściowego
a otaczającymi go ligandami jest wiązaniem jonowym

- rozpatruje wpływ pola ujemnych ligandów, traktowanych jako
ładunki punktowe, na energię orbitali d centralnego atomu
(jonu)

- pod wpływem tego oddziaływania następuje rozszczepienie
orbitali d na grupy o różnej energii zależnie od tego czy orbitale
d są skierowane wzdłuż osi x, y, z, czy też pomiędzy osiami

Teoria pola krystalicznego

x

x

y

y

z

z

d

d

d

xy

xz

y z

x

y

z

d

d

Z 2

X

2-Y 2

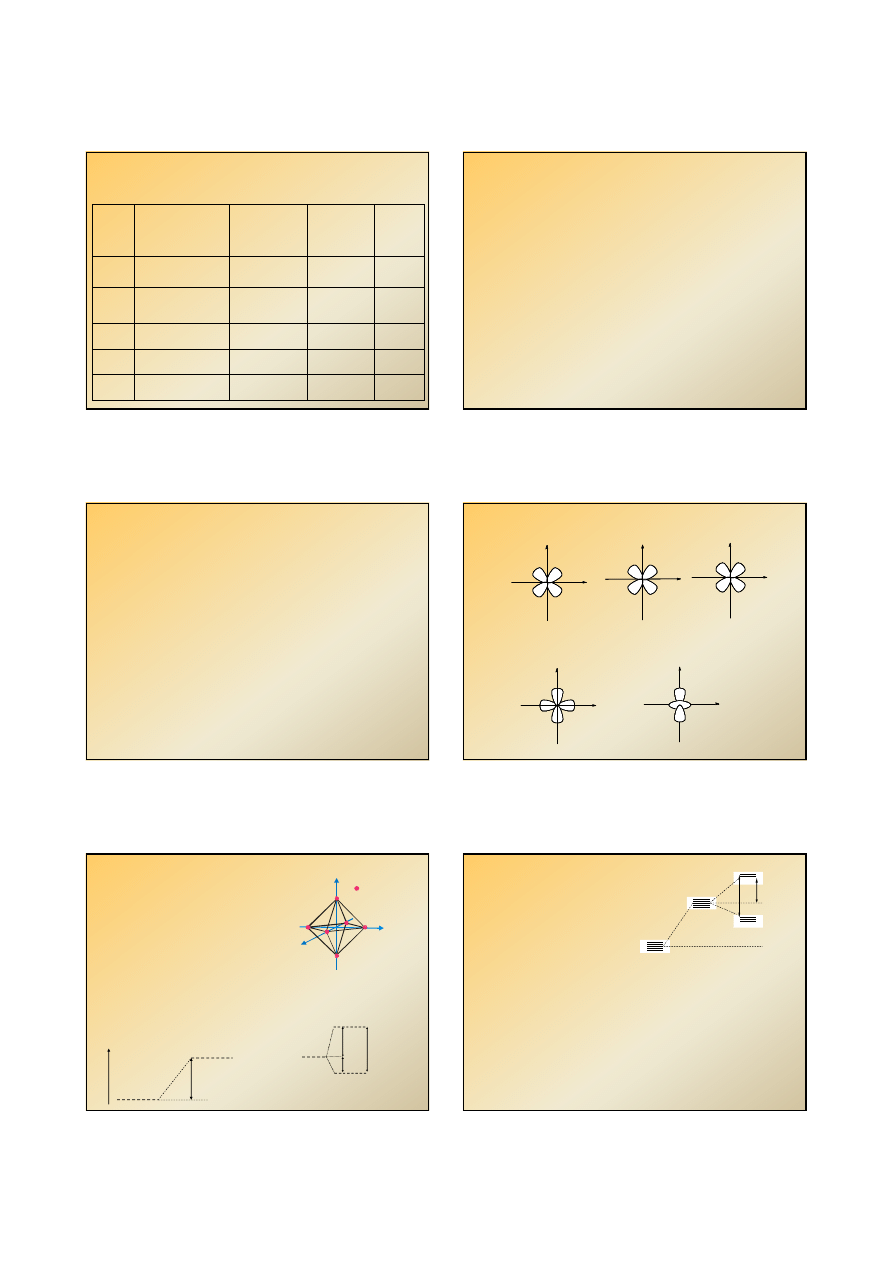
Kształty konturów orbitali d

pięciokrotnie zdegenerowany (bez pola ligandów)
poziom d ulega rozczepieniu na dwa podpoziomy:

e

g

–

dwukrotnie zdegenerowany poziom o wyższej energii

t

2g

–

trójkrotnie zdegenerowany poziom o niższej energii

e

g

atom w polu

sferycznym

E

0

d

n

t

2g

10Dq

6Dq

4Dq

atom swobodny atom w oktaedrycznym polu
ligandów

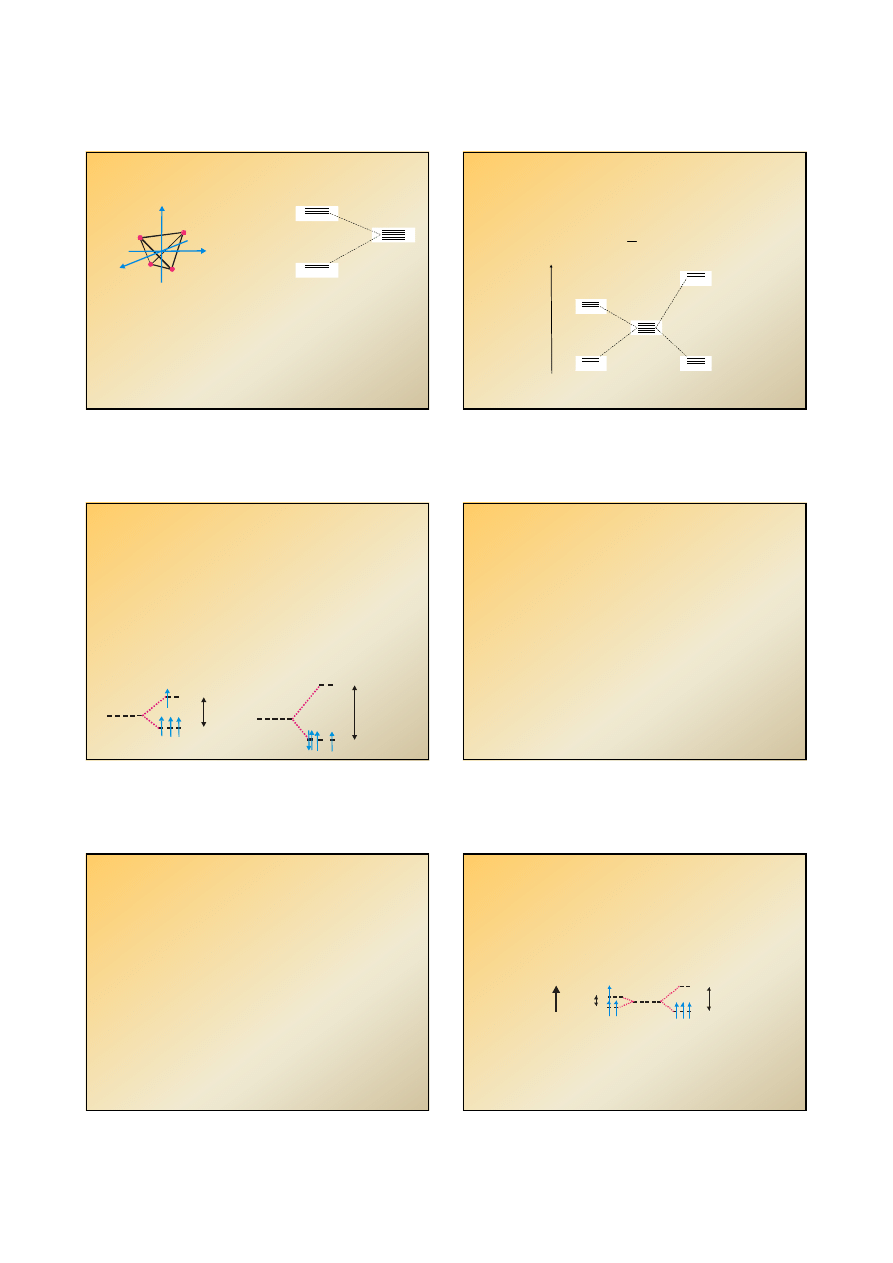
Teoria pola krystalicznego

x

y

z

ligandy

kompleksy
oktaedryczne

liczba koordynacji -

6

e

g

d’



+3/5

-2/5



t

2g

d

= 10Dq –

rozszczepienie

w polu krystalicznym

przykłady zmiany energii elektronów w polu krystalicznym:

1 elektron  zysk energii = 4Dq–energia stabilizacji

2 elektrony zysk energii = 24Dq-energia stabilizacji

6 elektronów zysk energii = 64Dq = 24Dq (

maksymalna

)

8 elektronów  zysk energii = 6  4Dq – 2  6Dq = 12Dq

10 elektronów  zysk energii = 6  4Dq – 4  6Dq = 0

2013-01-12

5

1.

Kolejność poziomów e i t

2g

odwrotna niż w przypadku kompleksów

oktaedrycznych (przyczyną jest to, iż ligandy zbliżają się z kierunków
leżących między osiami X,Y,Z).

2.

Energia rozczepienia w polu krystalicznym

dla kompleksów

tetraedrycznych

jest

znacznie

niższa

niż

dla

kompleksów

oktaedrycznych (na orbitale d atomu centralnego działa znacznie
mniejsza liczba ligandów )

kompleksy tetraedryczne

Teoria pola krystalicznego

x

y

z

liczba koordynacji -

4

atom w

oktaedrycznym

polu ligandów

atom w polu

sferycznym

okta

tetr

Dq

9

4

Dq



E

t

2

e

g

e

g

t

2g

sym. kulista

tetraedr

oktaedr

Rozszczepienie w polu

tetraedryczne i oktaedrycznym

1.

reguła wzrastającej energii

2. reguła Hunda

oczywiste są konfiguracje d

1

, d

2

, oraz d

3

wątpliwości zaczynają się od konfiguracji

d

4

możliwe są dwie konfiguracje:

(t

2g

)

3

(e

g

)

1

(t

2g-

)

4

4 elektrony niesparowane

2 elektrony niesparowane

konfiguracja wysokospinowa

konfiguracja niskospinowa

Zapełnianie orbitali

10 Dq(okta)

10 Dq(okta)

e

g

e

g

t

2 g

t

2g

l.k. = 6

l.k. = 6

4

3 d

Realizacja konfiguracji zależy od wartości rozszczepienia w polu
krystalicznym:

1. jeśli 10Dq < E

s

(energia sparowania elektronów) to tworzone są

kompleksy wysokospinowe

2. jeśli 10Dq > E

s

- powstają

kompleksy niskospinowe

Wartość energii rozszczepienia w polu krystalicznym

 (10Dq) jest

funkcją pola elektrycznego wytwarzanego przez ligandy (im
silniejsze pole tym większa wartość

).

Ligandy

ułożone

według

wyznaczonej

eksperymentalnie

wzrastającej wartości

 tworzą tzw.

szereg

szereg spektrochemiczny

spektrochemiczny::

I

-

<Br

-

<Cl

-

<F

-

<OH

-

<C

2

O

4

-

<H

2

O

O

2-

<NH

3

<NO

2

-

<<CN

-

wysokospinowe niskospinowe

Szereg spektrochemiczny

Wielkość rozczepienia w

polu krystalicznym :

1)

wartość  w kompleksach jonów danego okresu

przejściowego o tej samej wartościowości i z tymi samymi
ligandami jest w przybliżeniu stała (zmienia się w wąskich
granicach)

2)

wartość  w kompleksach tych samych ligandów szybko

rośnie ze wzrostem wartościowości kationu

3)

wartość  w kompleksach tych samych ligandów rośnie o

około 30% przy przejściu od jonu metalu jednego okresu
przejściowego do odpowiadającego mu jonu metalu

okresu

następnego

Cr

3+

:

1s

2

2s

2

p

6

3s

2

p

6

d

3

Dlaczego jony Cr

3+

wykazują preferencję do zajmowania

pozycji oktaedrycznych?

Energia

10 Dq(tetra)

10 Dq(okta)

e

g

e

t

2g

t

2

l.k. = 4

l.k. = 6

(CFSE)tetra

3,5 Dqokta

(CFSE)okta

12 Dqokta

= 2 x (6 Dqtetra) - 4 Dqtetra = 8 Dqtetra

8 Dqtetra x 4/9 =

= 3 x 4 Dqokta =

Energia stabilizacji jonów Cr

3+

w polu krystalicznym

(ang. Crystal Field Stabilization Energy)

2013-01-12

6

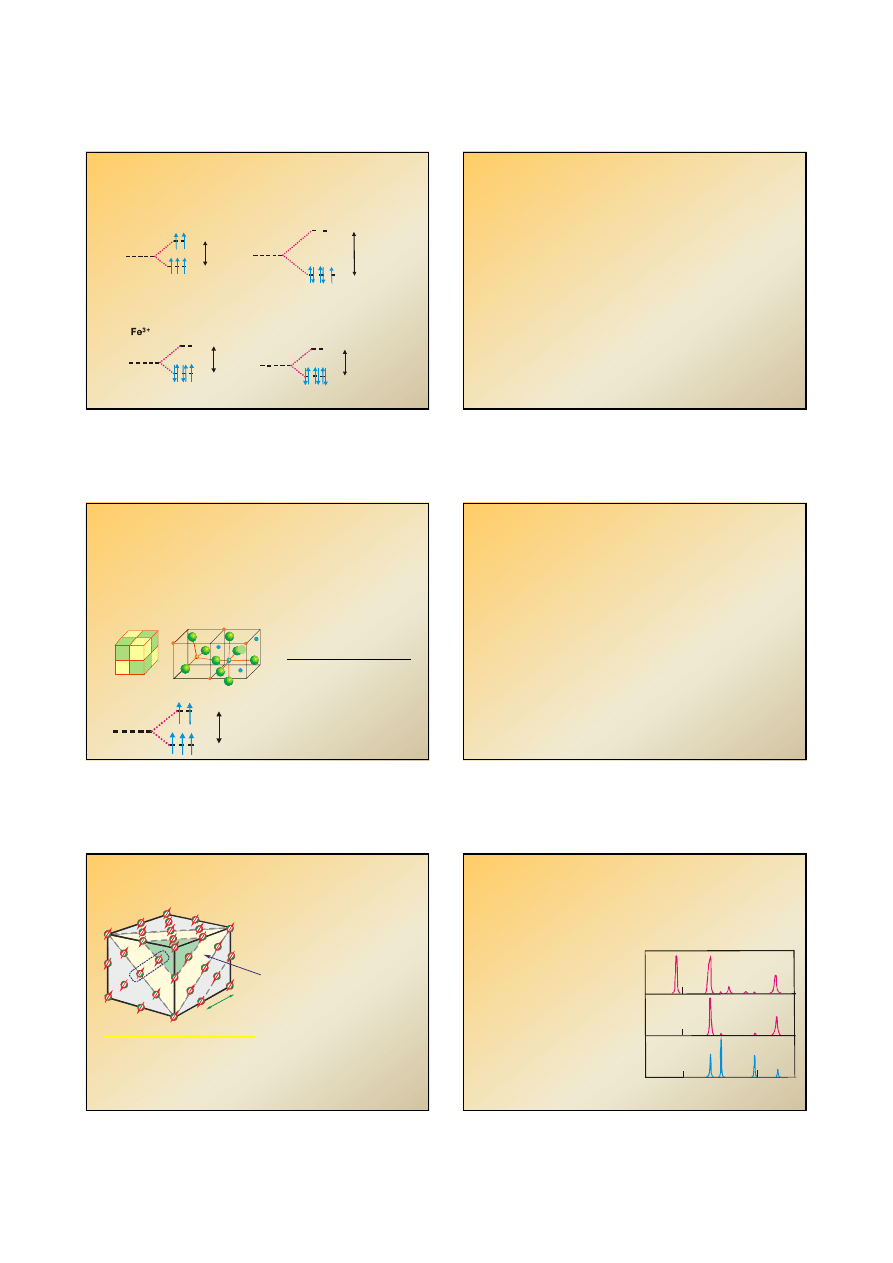
Kompleksy oktaedryczne wysoko- i nisko- spinowe

10 Dq(okta)

e

g

t

2g

l.k. = 6

wysoko-spinowy

nisko-spinowy

10 Dq(okta)

e

g

t

2g

l.k. = 6

np. d

5

, Fe

3+

Np. K

3

[FeF

6

]

Np.
K

3

[Fe(CN)

6

]

Różne stopnie utlenienia

10 Dq(okta)

10 Dq(okta)

e

g

e

g

t

2g

t

2g

l.k. = 6

l.k. = 6

diamagnetyczny

paramagnetyczny

Fe

2+

Przykłady

związki o ogólnym wzorze AB

2

O

4

– najczęściej

gdzie

A - metal z drugiej grupy układu okresowego lub metalem

przejściowym na drugim stopniu utlenienia,

B - metal z trzeciej grupy układu okresowego lub metalem

przejściowym na trzecim stopniu utlenienia.

Jony tlenkowe tworzą sieć

regularną o najgęstszym ułożeniu

, w

której występują

luki tetraedryczne

i

luki oktaedryczne

.

Komórka elementarna spinelu (8 AB

2

O

4

) obejmuje 32 jony tlenu, 64

luki tetraedryczne, z których 8 jest zajętych przez jony metalu, oraz
32 luki oktaedryczne, które są obsadzone w połowie.

spinel jest normalny

- jony M

2+

obsadzają luki tetraedryczne, a jony

M

3+

luki oktaedryczne

spinelu odwróconego

- połowa jonów M

3+

znajduje się w lukach

tetraedrycznych, a druga połowa wraz ze wszystkimi jonami M

2+

obsadza luki oktaedryczne, mówimy o strukturze

Spinele

4

3
2

2

O

B

A





- magnetyczne spinele,
- ważne z komercyjnych względów,
-MFe

2

O

4

, gdzie obok Fe

3+

występuje kation M

2+

, np. Fe

2+

, Ni

2+

, Cu

2+

.

Są to spinele częściowo lub całkowicie odwrócone, gdyż jon Fe

3+

o

konfiguracji d

5

nie ulega stabilizacji w pozycjach oktaedrycznych w

słabym polu krystalicznym ligandów tlenkowych. Duże jony M

2+

lokują

się w pozycjach oktaedrycznych, a Fe

3+

zostaje rozmieszczony

zarówno w lukach o symetrii tetraedrycznej jak oktaedrycznej.

A

B

A

B

O

2-

AB

2

O

4

A = Fe

2+

, Mn

2+

, Co

2+

, Zn

2+

B = Fe

3+

, Cr

3+

, Al

3+

, Mn

3+

luki T

d

64 1/8 8 8 A

spinel normalny [A]

T

[B

2

]

O

O

4

spinel odwrócony [B]

T

[AB]

O

O

4

10 Dq(okta)

e

g

t

2g

l.k. = 6

Fe

3+

Ferryty

Tlenki pierwszego szeregu przejściowego wykazują duże zróżnicowanie
własności w zależności od liczby atomowej i liczby elektronów d.

Tlenki

występujące

na

początku

pierwszego

szeregu

pierwiastków

przejściowych (Sc,

Ti, V, Cr

, Mn, Fe, Co, Ni, Cu) są

diamagnetyczne

(T

iO, VO,

CrO

). Elektrony d w tych tlenkach nie są zlokalizowane na indywidualnych

jonach M

2+

lecz zdelokalizowane na całą strukturę w częściowo zapełnionym

paśmie

t

2g

.

Nie

ma

magnetycznego

oddziaływania

pomiędzy

tymi

zdelokalizowanymi elektronami i w konsekwencji są to diamagnetyki i dobre
przewodniki elektryczności.

Dalsze tlenki w tym szeregu,

MnO, FeO, CoO i NiO

są

antyferromagnetyczne

w niskich temperaturach i przechodzą w paramagnetyki powyżej temperatury

Neela T

N

. W tych tlenkach elektrony d są zlokalizowane na poszczególnych

jonach M

2+

. Lokalizacja niesparowanych elektronów jest odpowiedzialna

zarówno za antyferromagnetyczne właściwości tych tlenków jak i za brak
przewodnictwa elektrycznego.

Tlenki metali przejściowych o

strukturze antyferromagnetycznej

(111)

a

MnO FeO CoO NiO

T

N

/

o

C -153 -75 -2 +250

Temperatura Neela wynosi
dla MnO -153

o

C (120 K),

dla FeO –75

o

C (198 K),

dla CoO -2

o

C (271 K),

a dla NiO 250

o

C (523 K).

Struktura jest taka sama w obu
zakresach temperatur, lecz np. NiO
poniżej 250

o

C ulega romboedrycznej

dystorsji.

W NiO zachodzi słaba kontrakcja
struktury

wzdłuż

jednej

z

trójkrotnych osi równoległych do
kierunku [111].

Podobna

kontrakcja

zachodzi

w

MnO, lecz np. w FeO przeciwnie,
struktura jest nieco wydłużona.

neutrony, 80 K

neutrony, 293 K

RTG, 293 K

a = 8,85 A

a = 4,43 A

a = 4,43 A

111

111

222

111

200

220

311

200

220

311

622

511

331

0

20

40

60

80

2Θ/

o

MnO

Struktury antyferromagnetyczne można badać metodą

dyfrakcji neutronów

.

Dwa

rodzaje

rozpraszania

uczestniczą

w

tak

otrzymanym

obrazie

dyfrakcyjnym:

rozpraszanie przez jądra atomowe

i przez

niesparowane

elektrony

. Pierwsze daje obraz podobny do dyfrakcji rentgenowskiej, choć

intensywności mogą być nieco różne.

W przypadku struktur

antyferromagnetycznych

występuje także

drugi typ rozpraszania powodujący
pojawienie się

dodatkowych linii

w

dyfraktogramie neutronowym.

Jest on skutkiem

kooperatywnego

oddziaływania

pomiędzy

niesparowanymi

elektronami

, co może powodować

powstanie nadstruktury.

Ponadto, zachodzi

silne rozpraszanie

neutronów

przez niesparowane elektrony,

podczas gdy promienie rentgenowskie nie
ulegają takiemu rozpraszaniu.

Dyfrakcja neutronów