Temat: Wyznaczanie ciepła właściwego ciał stałych.

Teoria kinetyczno - molekularna budowy materii przyjmuje, ze ciała zbudowane są z atomów lub cząstek. Elementy tych ciał znajdują się w ciągłym ruchu. Do określenia położenia cząstki potrzebna jest minimalna liczba współrzędnych czyli tzw. Liczba stopni swobody. Zasada ekwipatrycji energii głosi, że na każdy stopień swobody cząsteczki gazu przypada średnio ta sama ilość energii równa:

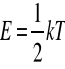
gdzie:

E - średnia wartość energii przypadająca na stopień swobody

k - stała Boltzmanna

T - temperatura w skali Kelvina

Wzrostowi energii kinetycznej towarzyszy wzrost temperatury, dlatego definiujemy ją jako miarę energii kinetycznej przypadającej na jeden stopień swobody.

Sumaryczną energię wszystkich cząstek nazywać będziemy energią wewnętrzną. Energia ta może być przekazywana między dwoma ciałami w kierunku malejącej temperatury. Ilość energii, którą pobiera jednostka masy ciała na podgrzanie o jeden stopień K nazywa się ciepłem właściwym. Z tej definicji wynika, że dowolna masa m przy ogrzaniu o dowolny przyrost temperatury
pobiera tej energii:

gdzie:

Q - ilość ciepła pobranego

c - ciepło właściwe

m - masa ciała

Ciepłem nazywamy energię przepływającą między ciałami w wyniku różnicy temperatur. W każdej wymianie ciepła biorą udział co najmniej dwa ciała lub układ ciał. Prawo bilansu cieplnego głosi, że w układzie izolowanym termicznie ilość ciepła oddanego przez jedno ciało jest równa ilości ciepła pobranego przez inne ciało układu.

Ciepło pobrane przez kalorymetr i wodę oblicza się w następujący sposób:

gdzie:

- odpowiednio ciepło właściwe wody i kalorymetru

- temperatura końcowa i początkowa

- masa wody i kalorymetru

Z podanego wyrażenia obliczamy ciepło oddane:

Prawo bilansu cieplnego pozwala porównać prawe strony tych równań.

Opis ćwiczenia:

1. Ważymy część wewnętrzną kalorymetru

2. Część wewnętrzną kalorymetru napełniamy do połowy wodą i ponownie ważymy

3. Ogrzewamy badane ciało

4. Ciało ogrzane wkładamy do kalorymetru

5. Przeprowadzamy pomiar temperatur

6. Wykreślamy wykres zależności temperatury od czasu

7. Wyznaczamy na wykresie szukane temperatury
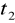
   i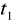
   

Tabele pomiarowe:

Lp.	Masa kalorymetru [g]	Masa kalorymetru i wody [g]	Masa badanego ciała [g]
1	63,90	210,00	120,00 - Cu
2	63,90	214,70	36,00 -Al.
3	63,90	215,75	110,75 - Fe

Dla ciała 1:

1. zmiany temperatury wody w czasie:

Czas	0	30	60	90	120	150	180	210	240	270	300
Temperatura	22,0	22,1	22,1	22,1	22,2	22,2	22,2	22,2	22,2	22,2	22,2

2. zmiany temperatury ciała w czasie:

Czas	0	15	30	45	60	75	90	105	120	135	150
Temperatura	22,2	22,6	24,5	25,9	26,0	26,0	26,0	26,0	26,0	26,0	26,0
Czas	165	180	195	210	225	240	255	270	285	300
Temperatura	26,0	26,0	26,0	26,0	26,0	26,0	26,0	26,0	26,0	26,0

Dla ciała 2:

1. zmiany temperatury wody w czasie:

Czas	0	30	60	90	120	150	180	210	240	270	300
Temperatura	22,3	22,3	22,3	22,3	22,4	22,4	22,4	22,4	22,4	22,4	22,4

2. zmiany temperatury ciała w czasie:

Czas	0	15	30	45	60	75	90	105	120	135	150
Temperatura	22,4	24,9	25,1	25,4	25,4	25,4	25,4	25,4	25,4	25,4	25,4
Czas	165	180	195	210	225	240	255	270	285	300
Temperatura	25,4	25,4	25,4	25,4	25,4	25,4	25,4	25,4	25,4	25,4

Dla ciała 3:

1. zmiany temperatury wody w czasie:

Czas	0	30	60	90	120	150	180	210	240	270	300
Temperatura	22,2	22,1	22,1	22,1	22,1	22,1	22,1	22,1	22,1	22,1	22,1

2. zmiany temperatury ciała w czasie:

Czas	0	15	30	45	60	75	90	105	120	135	150
Temperatura	22,2	24,3	24,7	25,4	25,5	25,7	25,8	25,8	25,9	26,0	26,0
Czas	165	180	195	210	225	240	255	270	285	300
Temperatura	26,1	26,1	26,1	26,1	26,2	26,2	26,2	26,2	26,2	26,2

Temperatury badanych ciał w chwili wkładania do kalorymetru wynosiły :

-aluminium T_Al = 90 °C

-miedź T_Cu= 90 °C

-żelazo T_Fe= 90 °C

Dokładności pomiarowe:

Obliczenia:

Ciepło właściwe poszczególnych ciał możemy obliczyć ze wzorów:

Ciepło właściwe aluminium :

Ciepło właściwe miedzi i żelaza :

Gdzie : - m_Al , m_Cu , m_Fe - masy badanych ciał

- m_w , c_w - masa i ciepło właściwe wody

- m_k - masa kalorymetru

- t₁ , t₂ , t₃ - temperatury odpowiednio : początkowa układu woda - kalo- rymetr ; końcowa całego układu (woda , kalorymetr , badane ciało) ; początkowa badanego ciała .

Ciało:	1 - Miedź	2 - Aluminium	3 - Żelazo
Ciepło właściwe: [J/kgK]	340	888	402

Dyskusja błędów:

1. Aluminium

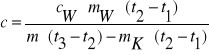
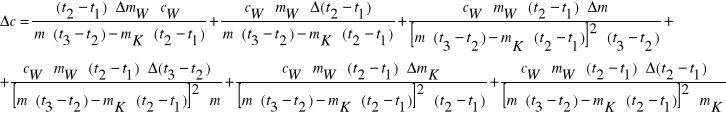
2. Żelazo i Miedź

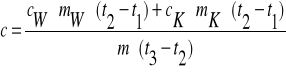
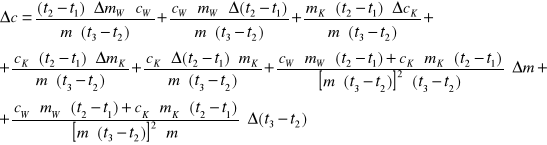
Ciało:	1 - Miedź	2 - Aluminium	3 - Żelazo
Błąd: [J/kgK]	19,4	59,5	22,0

1. Ciało I - Miedź

2. Ciało II - Aluminium

3. Ciało III - Żelazo

Wnioski :

Uzyskane wartości ciepła właściwego są dość bliskie wartościom odczytanym z tablic, z wyjątkiem żelaza, czego przyczyną mogło być to, iż badanym ciałem nie było czyste żelazo lub był to jakiś stop. Sugeruje to dość dobrą dokładność tej metody na miarę warunków.

Ponadto na błędy pomiarów mogły wpłynąć następujące czynniki :

- ochłodzenie się badanego ciała przy jego przenoszeniu z cylindra do kalorymetru ,

- trudność w jednoczesnym wychwyceniu czasu i temperatury na odcinku gwałtownego skoku temperatury ,

• niedokładności w wyznaczeniu temperatur t₁ i t₂ spowodowana trudnością dobrania prostej dzielącej odcinek charakterystyki , odpowiadający wymianie ciepła badanego ciała z układem woda-kalorymetr , na dwa równe sobie pola .

• brak ciągłego mieszania wody w kalorymetrze.

1

1

---