Wyznaczenie ciepła właściwego
ciał stałych
przy użyciu kalorymetru
Ćwiczenie nr 26
Opis teoretyczny
Temperatura - jest to wielkość skalarna, będąca właściwością wszystkich układów termodynamicznych. Wielkość ta opisuje ciepłotę danego ciała.
Ciepło - jest energią, która przenosi się między układem i jego otoczeniem (lub między ciałem a ciałem) jedynie w wyniku różnicy temperatur. Jest związane ze zmianą energii ruchu nieuporządkowanego cząsteczek. Pomiarami ilości ciepła zajmuje się kalorymetria. Jest to dziedzina fizyki doświadczalnej, oparta na poniższych zasadach:
Ilość ciepła
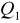
oddanego przez badane ciało jest równa ilości ciepła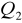
pobranej przez otoczenie (lub inne ciała).Ilość ciepła pobrana przez ciało ogrzewane jest równa ilości ciepła oddanej w czasie stygnięcia (w tym samym zakresie temperatur), jeśli proces zachodzi w odwrotnym kierunku przez te same punkty pośrednie.
Ilość ciepła pobrana lub oddana przez ciało jednorodne jest proporcjonalna do jego masy, a przy niewielkich zmianach temperatury - także do przyrostu temperatury
![]()
![]()
Pojemność cieplna - jest to ilość ciepła dostarczana ciału przy podwyższaniu temperatury o 1 stopień Celsjusza. Z pojęciem tym wiąże się inne - ciepło właściwe. Jest to pojemność cieplna przypadająca na jednostkę masy.
Klasyczna teoria ciepła właściwego oparta jest na zasadzie ekwipartycji energii, która mówi, że gdy liczba punktów materialnych jest bardzo duża i obowiązuje mechanika newtonowska, wtedy wszystkie rodzaje energii (kinetyczna ruchu postępowego, rotacji i oscylacji oraz potencjalna drgań atomów) mają tą samą wartość średnią, zależną wyłącznie od temperatury. Innymi słowy, dostępna energia zależy wyłącznie od temperatury i rozkłada się w równych porcjach na wszystkie sposoby, w jakie cząsteczki mogą ją absorbować. Każdy „taki sposób” nazywany jest stopniem swobody. Zgodnie z tą zasadą średnia energia ruchu cieplnego przypadająca na jeden stopień swobody wynosi k![]()
T/2. Dla gazu doskonałego mamy więc:
- gaz jednoatomowy C = 3RT/2 ; - dwuatomowy C = 5RT/2 ; - wieloatomowy C = 6RT/2.
Energia wewnętrzna ciał stałych (część zależna od temperatury) określona jest poprzez drgania węzłów sieci krystalicznej.
W 1819 roku Dulong i Petit zauważyli, że ciepło atomowe wszystkich pierwiastków w stanie stałym (poza węglem, borem, krzemem) jest w przybliżeniu jednakowe i wynosi 6cal/gramoatom![]()
K=25.14J/mol![]()
K. Sieć krystaliczna ciał jednoatomowych i N węzłach posiada 3N stopni swobody, a więc ciepło atomowe wynosi 3Nk.
Pojemność cieplna jak i ciepło właściwe nie są stałe, ale zależne od położenia przedziału temperatur.
Jednostka ciepła - ilość ciepła dostarczona aby ogrzać jeden kilogram wody od temperatury 14,5 ![]()
do 15,5 ![]()
- nosi nazwę jednej kilokalorii (kcal). Używa się także jako jednostki ciepła kalorii (cal = ![]()
kcal).
![]()
![]()
![]()
- pojemność cieplna ![]()
- ciepło właściwe w dowolnej temperaturze
![]()
- ciepło właściwe (średnie w wybranym przedziale temperatur)
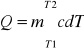
- ciepło potrzebne ciału o masie m. i cieple właściwym c, aby podnieść jego temperaturę od T1 do T2
Zasada zachowania energii w odniesieniu do ciepła (bilans cieplny) - wymiana energii tylko w postaci ciepła między ciałami o różnych temperaturach. Aby zaistniała zasada zachowania energii układ musi być odizolowany. Dość dobrym przykładem takiego układu jest kalorymetr.
Wymiana ciepła w kalorymetrze trwa określoną ilość czasu - temperatura zmienia się stopniowo. Aby przybliżyć rzeczywisty {linia ciągła} przebieg wymiany ciepła do idealnego {przerywana} (tj. nieskończenie krótki czas wymiany ciepła) używa się metody interpolacji.
Metodą posługujemy się aby wyznaczyć temperaturę wody początkową T0 i końcową Tk.
Badane ciało o masie m i temperaturze t oddaje kalorymetrowi z wodą ciepło:
![]()
.
Woda w kalorymetrze i kalorymetr pobiorą ciepło:
![]()
(gdzie ![]()
odpowiednio ciepła właściwe wody i kalorymetru).
Zgodnie z zasadami kalorymetrii, ciepła te równają się, a dzięki temu możemy wyliczyć ciepło właściwe badanego ciała ![]()
:
![]()
.
Przebieg doświadczenia i obliczenia
Wykonywanie ćwiczenia rozpoczęliśmy od dokładnego zważenia badanych ciał i kalorymetru wraz z mieszadełkiem. Po napełnieniu kalorymetru wodą i ponownym jego zważeniu wyznaczyliśmy masę wody. Przez 5 minut przed wrzuceniem ciała (umieszczonego już w ogrzewaczu parowym) do kalorymetru dokonywaliśmy pomiaru temperatury w 30-sekundowych odstępach czasu. Po szybkim przeniesieniu badanego ciała z ogrzewacza do kalorymetru kontynuowaliśmy pomiar temperatury jeszcze przez 10 minut. Postępowanie było powtórzone dla pozostałych dwóch ciał.
Ciepło właściwe obliczamy ze wzoru:
![]()
![]()
Rachunki można wykonywać w ![]()
, gdyż przy dzieleniu skracają się różnice temperatur.
Temperaturę ciała odczytujemy na podstawie ciśnienia atmosferycznego, które wynosi 754,4 mmHg. Temperatura wrzenia wody przy takim ciśnieniu wynosi t=99,8°C, która jest równa temperaturze ciała w momencie umieszczania w kalorymetrze
![]()
[kg] - masa kalorymetru z mieszadełkiem
![]()
[J/kgK] - ciepło wł. kalorymetru
![]()
[J/kgK] - ciepło właściwe wody
Temperaturę początkową T0 i końcową Tk odczytujemy z wykresów (Rysunki 1,2,3).
Obliczenia dla ciała 1
![]()
[kg] - masa ciała 1 ![]()
[kg] - masa wody dla doświadczenia 1
![]()
- temperatura początkowa ![]()
- temperatura końcowa
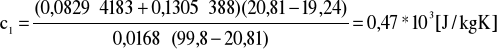
Obliczenia dla ciała 2
![]()
[kg] - masa ciała 2 ![]()
[kg] - masa wody dla doświadczenia 2
![]()
- temperatura początkowa ![]()
- temperatura końcowa
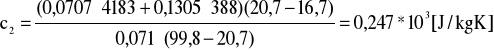
Obliczenia dla ciała 3
![]()
[kg] - masa ciała 3 ![]()
[kg] - masa wody dla doświadczenia 3
![]()
- temperatura początkowa ![]()
- temperatura końcowa
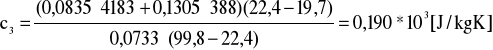
Analiza błędów
Rachunek błędu wykonujemy metodą różniczki zupełnej.
![]()
Dla ułatwienia obliczeń przyjmuję Y=Tk-T0, pamiętając, że ![]()
oraz X= t - Tk i ![]()
![]()
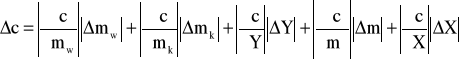
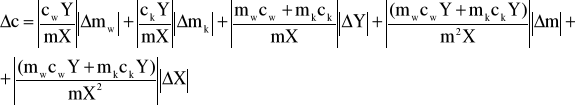
Obliczenia wykonywałem w Excelu
Błąd dla ciała 1:
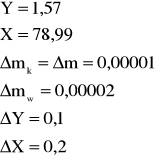
![]()
- błąd bezwzględny;
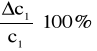
13% - błąd względny.
Błąd dla ciała 2:
ΔY=4
![]()
ΔX=79,1
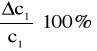
5,2% - błąd względny.
Błąd dla ciała 3:
ΔY=2,7
![]()
ΔX=77,4
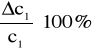
7,6% - błąd względny.
UWAGA: Wszystkie błędy ![]()
!
Wnioski:
W naszym doświadczeniu obliczyliśmy ciepło właściwe dla trzech ciał stałych. Jednakże biorąc pod uwagę analizę błędów, to można powiedzieć, iż błąd wyznaczenia ciepła właściwego jest znaczny - 10%. We wszystkich trzech doświadczeniach główną odpowiedzialnością za błąd można obarczyć niedokładność pomiaru temperatury największy składnik sumy różniczek). Umieszczenie ciała 1 (bardzo lekkiego w porównaniu z pozostałymi) w kalorymetrze spowodowało mały skok temperatury (zaledwie 0,7![]()
) co przy dokładności mierzenia 0,1![]()
skutkuje dużym błędem wyliczonego ciepła właściwego.
Mimo to, że wielkość błędów sugeruje, iż uzyskany wynik jest dobrym przybliżeniem wartości rzeczywistych należy pamiętać o pewnych założeniach. Po pierwsze uznaliśmy kalorymetr za układ w którym zachodzi wymiana energii jedynie między ciałem i wodą. Jest to niestety idealizacja - część ciepła „ucieka” do otoczenia. Po drugie temperaturę początkową ciała przyjęliśmy jako tablicową temperaturę wrzenia wody w ogrzewaczu parowym. Mimo wielkich starań czas przenoszenia ciała z ogrzewacza do kalorymetru nie był nieskończenie krótki. Skutkiem tego jest minimalne ochłodzenie ciała.
Wady tej metody wyznaczania ciepła właściwego nie skreślają jej jednak jako dobrej - tym bardziej, że w odpowiednich warunkach osiągane wyniki mogą być dokładniejsze.
Porównując nasze wyniki z danymi tablicowymi, można stwierdzić, co to były za ciała. Pierwsze ciało ma porównywalną wartość ciepła właściwego (w granicach błędu) z cyną, której wartość wynosi c=384 [J/kg*K]. Drugie ciało jest wykonane ze srebra. Ciepło właściwe wynosi c=234[J/kg*K]. Natomiast trzecie ciało, według mnie, jest wykonane z platyny (ciepło właściwe c=136[J/kg*K]. Jednakże patrząc na wykres trzeci można powiedzieć, iż doświadczenie to wykonane było nie do końca poprawnie i dlatego nie jestem pewien, iż ciało trzecie jest z platyny.
Można także dodać, iż najdokładniej wykonane zostało przeprowadzone doświadczenie w przypadku drugiego ciała. Zmieniliśmy tam metodę działania i zwiększyliśmy częstotliwość odczytywania temperatury (odczytywaliśmy ją co kilkanaście sekund na początku po wrzuceniu ciała). Metoda ta pozwala na dokładniej sporządzić wykres i dokładniej odczytać temperaturę początkową i końcową.
1
4
Marcin Grześczyk
I rok „bis” - Fizyka
17.12.1999
dr T. Biernat
![]()
![]()
![]()
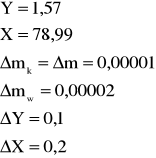
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
SPR26, Studia, Pracownie, I pracownia, 26 Wyznaczanie ciepła właściwego ciał stałych metodą kaloryme
26 Wyznaczanie ciepła właściwego ciał stałych metodą kalorymetryczną G Szcześniak
Wyznaczanie ciepla wlasciwego cial stalych metoda kalorymetryczna
Laboratorium Podstaw Fizyki spr( Wyznaczanie ciepła właściwego ciał stałych metodą kalorymetryczną
wyznaczanie Ciepła właściwego ciał stałych - 1
Wyznaczanie ciepła właściwego ciał stałych, Automatyka i Robotyka Rok I
Wyznaczanie ciepła właściwego ciał stałych, Automatyka i Robotyka Rok I
WYZNACZANIE ZALEZNOSCI CIEPLA WLASCIWEGO CIAL STALYCH OD TEMPERATURY 2
wyznaczanie ciepła właściego ciał stałych, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza la
INSTRUKCJE, cw26, WYZNACZANIE CIEPŁA WŁAŚCIWEGO CIAŁ STAŁYCH
WYZNACZANIE CIEPŁA WŁAŚCIWEGO CIAŁ STAŁYCH 2
WYZNACZANIE CIEPŁA WŁAŚCIWEGO CIAŁ STAŁYCH
,Laboratorium podstaw fizyki, WYZNACZANIE ZALEZNOSCI CIEPLA WLASCIWEGO CIAL STALYCH OD TEMPERATURYx
,laboratorium podstaw fizyki,WYZNACZANIE ZALEZNOSCI CIEPLA WLASCIWEGO CIAL STALYCH OD TEMPERATURY
Wyznaczanie zależności ciepła właściwego ciał stałych od temperatury
Wyznaczenie ciepła właściwego ciał stałych
więcej podobnych podstron