Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 1.
Wykonujemy rzuty symetryczną kością do gry do chwili uzyskania drugiej „szóstki”.
Niech Y oznacza zmienną losową równą liczbie rzutów, w których uzyskaliśmy inne
wyniki niż „szóstka”, a X zmienną losową równą liczbie rzutów, w których
uzyskaliśmy „jedynkę”. Oblicz
)
4
|
(
=
−
X
X
Y
E
.
(A) 12
(B) 14
(C) 16
(D) 18
(E) 20
1
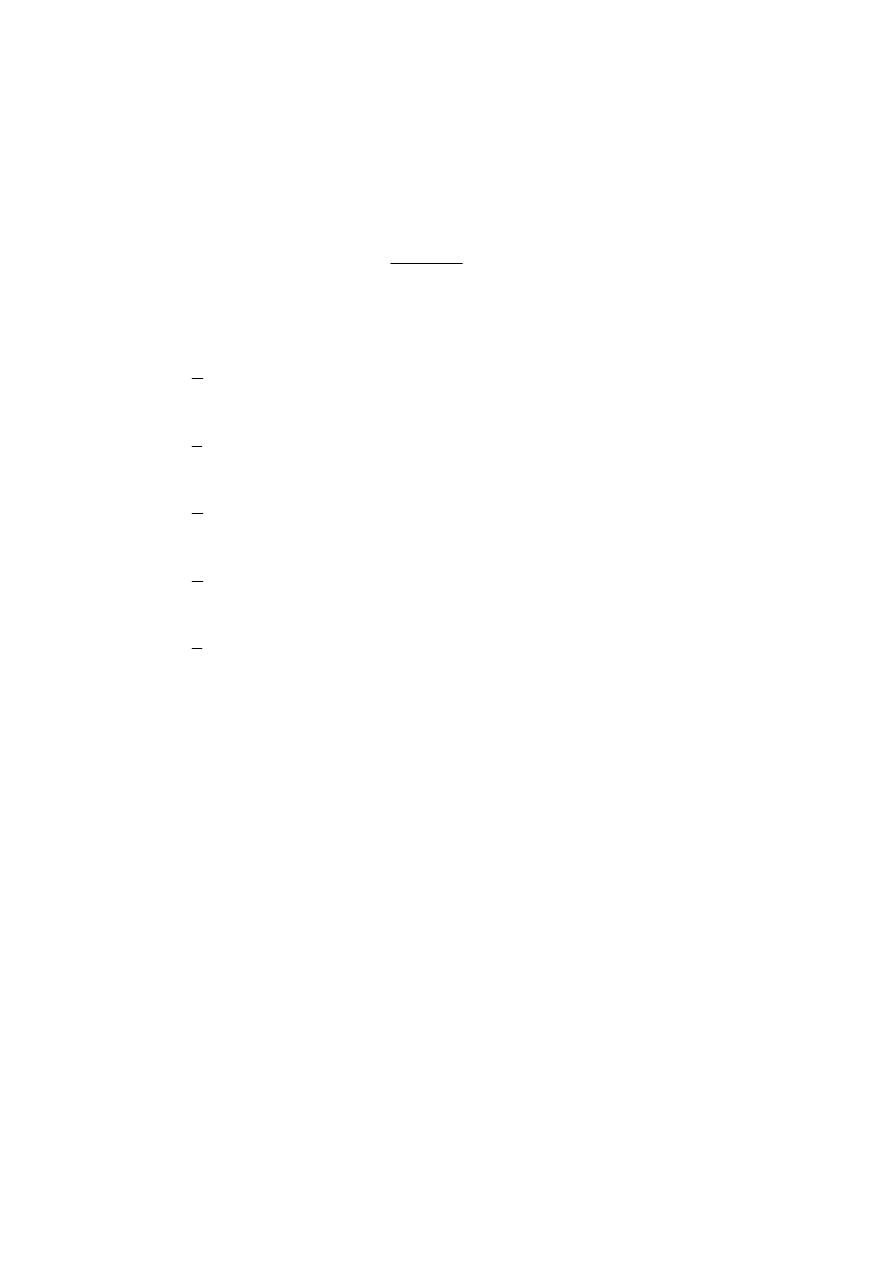
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 2.
Niech
będą niezależnymi zmiennymi losowymi, przy czym
ma
rozkład Pareto(1,1) a
mają jednakowy rozkład Pareto (1,2). Oblicz
4
3
2
1
,
,
,
X
X
X
X
X
1
X
4
3
2
,
,
X
X
))
,
,
(
max
)
,
,
(
min
(
4
3
2
1
4
3
2
X
X
X
X
X
X
X
P
<
<
.
Rozkład Pareto
)
,
(
θ
λ
jest rozkładem o gęstości
≤
>
+
=
+
.
0
gdy
0
0
gdy
)
(
)
(
1
x
x
x
x
f
θ
θ
λ
θ
λ
(A)
5
2
(B)
3
1
(C)
2
1
(D)
3
2
(E)
5
3
2
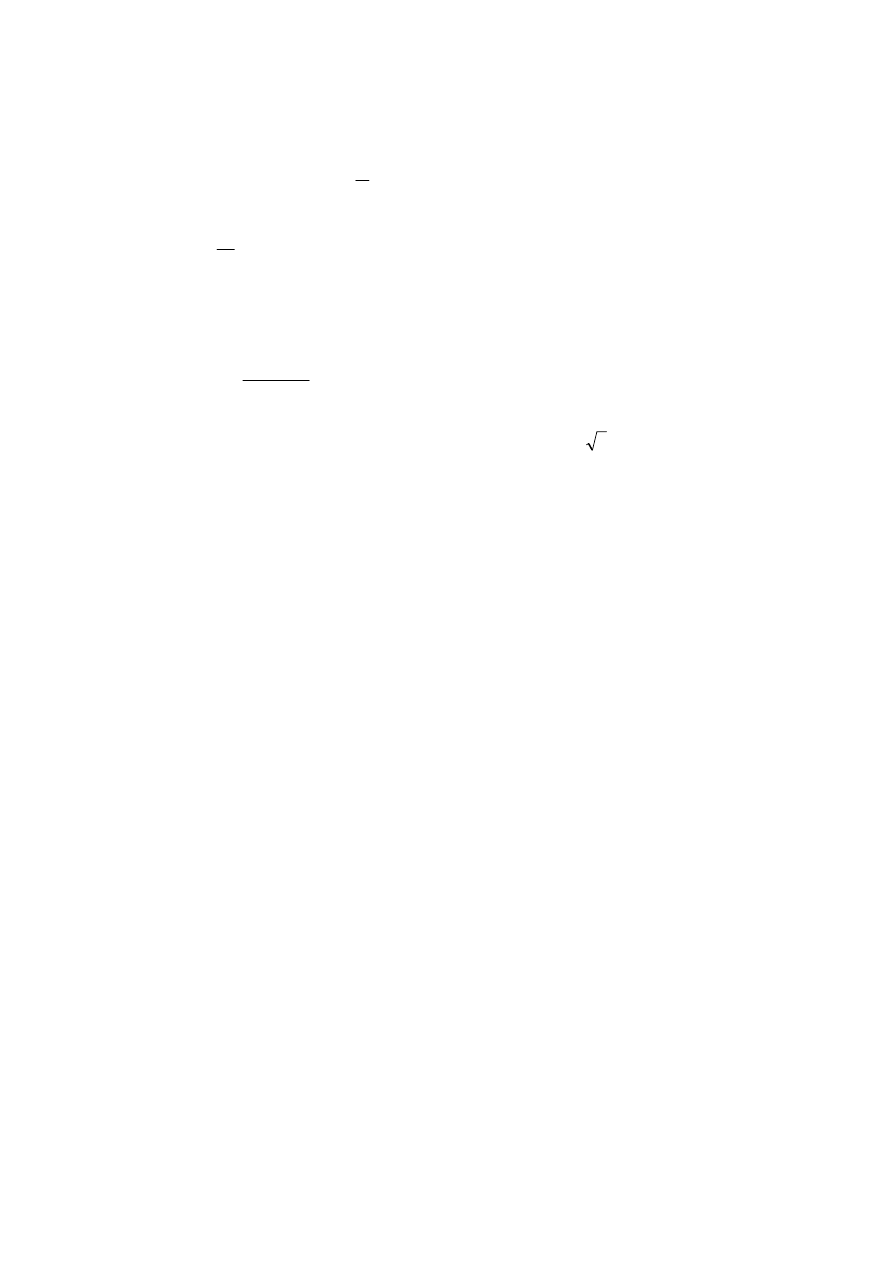
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 3.
Niech będzie dwuwymiarową zmienną losową o funkcji gęstości
)
,
(
Y
X
<
+
>
>
=
przypadku.
przeciwnym
w
0
1
i
0
i
0
gdy
4
)
,
(
2
2
y
x
y
x
y
x
f
π
Niech
X
Y
Z
=
i V
. Wtedy łączny rozkład zmiennych Z, V jest taki, że
2
2
Y
X
+
=
(A)
1
=
EZ
(B) funkcja
gęstości rozkładu brzegowego zmiennej
Z wyraża się wzorem
)
1
(
2
)
(
2
z
z
g
+
=
π
dla
)
,
0
(
+∞
∈
z
(C)
mediana rozkładu brzegowego zmiennej Z jest równa 3
(D) zmienne
Z i V są zależne
(E) funkcja
gęstości rozkładu brzegowego zmiennej V wyraża się wzorem
dla v
3
4
)
(
v
v
g
V
=
)
1
,
0
(
∈
3
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 4.
Niech
będą zmiennymi losowymi o rozkładzie normalnym
każda i Y
zmiennymi losowymi o rozkładzie normalnym
każda.
Wszystkie zmienne są niezależne. Hipotezę
m
X
X
X
,
,
,
2
1
K
n
Y
Y
,
,
,
2
1
K
)
,
(
2
1
σ
µ
N
)
2
σ
,
(
2
µ
N
2
1
0
:
µ
µ
=
H
przy alternatywie
2
1
:
1
µ
µ
>
X
X
X
,
,
,
2
1
K
0
H
H
weryfikujemy w następujący sposób. Zliczamy liczbę S elementów w
próbce
większych od wszystkich elementów próbki Y
.
Hipotezę
odrzucamy, gdy
, gdzie s jest wartością krytyczną. Przypuśćmy,
że m=7 i n=8. Podaj rozmiar testu, gdy s=2.
m
n
Y
Y
,
,
,
2
1
K
s
S
≥
(A)
0,15
(B) 0,10
(C) 0,20
(D)
0,05
(E)
0,25
4
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 5.
Niech
będą niezależnymi zmiennymi losowymi z rozkładu o gęstości
n
X
X
X
,
,
,
2
1
K
∉
∈
=
).
1
;
0
(
gdy
0
)
1
;
0
(
gdy
2
)
(
x
x
x
x
f
θ
Niech
∏
=
=
n
i
n
i
n
X
1
1
T
.
Które z poniższych stwierdzeń jest prawdziwe?
(A)
023
,
0
}
2
)
{(
lim
5
,
0
5
,
0
=
>
−
−
−
∞
→
e
n
e
T
P
n
n
(B)
023
,
0
}
2
|
{|
lim
5
,
0
5
,
0
=
>
−
∞
→
e
n
e
T
P
n
n
(C)
1
}
{
lim
5
,
0
=
<
−
∞
→
e
T
P
n
n
(D)
046
,
0
}
|
{|
lim
5
,
0
5
,
0
=
>
−
−
−
∞
→
e
n
e
T
P
n
n
(E)
1
}
{
lim
5
,
0
=
>
∞
→
e
T
P
n
n
5
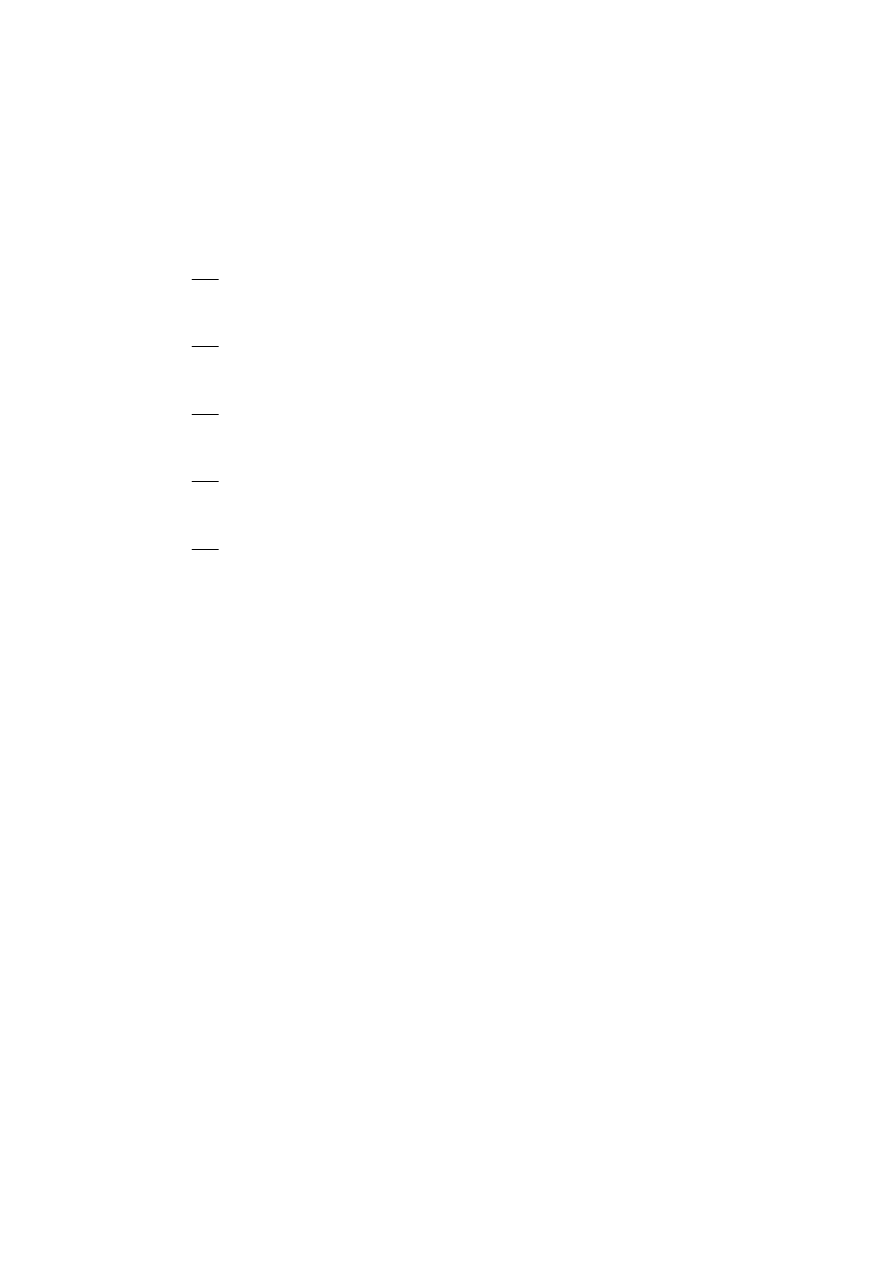
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie 6.
Ustawiamy w ciąg 6 elementów typu a i 9 elementów typu b. Wszystkie ciągi są
jednakowo prawdopodobne. Serią nazywamy ciąg elementów jednego typu, przed i za
którym występuje element drugiego typu, na przykład w ciągu : aaabbbbaabbbbba
jest 5 serii (3 serie elementów typu a i 2 serie elementów typu b). Oblicz
prawdopodobieństwo, że w ciągu będzie 6 serii.
(A)
143
8
(B)
143
96
(C)
143
16
(D)
143
48
(E)
143
24
6
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie
7.
Niech
będą niezależnymi zmiennymi losowymi, przy czym zmienne
losowe
i
mają rozkład Weibulla o gęstości
n
m
X
X
X
+
,
,
,
2
1
K
i
X
m
K
,
2
,
1
=
≤
>
=
−
0
gdy
0
0
gdy
2
)
(
x
x
e
x
x
f
x
θ
θ
θ
a
, i
i
X
n
m
m
m
+
+
+
=
,
,
2
,
1
K
są zmiennymi losowymi o rozkładzie Weibulla o
gęstości
≤
>
=
−
0
gdy
0
0
gdy
)
(
2
x
x
e
x
x
g
x
θ
θ
θ
,
gdzie
0
>
θ
jest nieznanym parametrem. Jeśli
5
=
= n
m
, to błąd średniokwadratowy
estymatora największej wiarogodności wyznaczonego na podstawie próby
jest równy
n
m
X
X
+
,
1
X
,
,
2
K
(A)
2
3
2
θ
(B)
2
3
1
θ
(C)
2
θ
(D)
2
9
1
θ
(E)
2
6
1
θ
7
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie
8.
Niech
będą zmiennymi losowymi o rozkładzie Pareto
a
będą zmiennymi losowymi o rozkładzie Pareto
(
, gdzie
a
są
nieznanymi parametrami. Wszystkie zmienne są niezależne. Na poziomie ufności
n
X
X
X
,
,
,
2
1
K
m
Y
,
K
)
,
1
(
1
a
0
2
>
a
Y
Y
,
,
2
1
)
,
1
2
a
,
1
α
−
1
budujemy przedział ufności dla ilorazu parametrów
]
,
[
cT
dT
2
1
a
a
na podstawie
estymatora największej wiarogodności T tego ilorazu w ten sposób, że
2
)
(
)
(
2
1
,
2
1
,
2
1
2
1
α
=
>
=
<
a
a
dT
P
a
a
cT
P
a
a
a
a
.
Jeśli 1
,
0
=
α
i m=4 i n=5, to przedział ufności ma długość
(A) 3,02T
(B) 2,77T
(C) 6,06T
(D) 5,03T
(E) 4,42T
Uwaga:
Rozkład Pareto (
)
,
θ
λ
jest rozkładem o gęstości
≤
>
+
=
+
0
gdy
0
0
gdy
)
(
)
(
1
x
x
x
x
f
θ
θ
λ
θ
λ
8
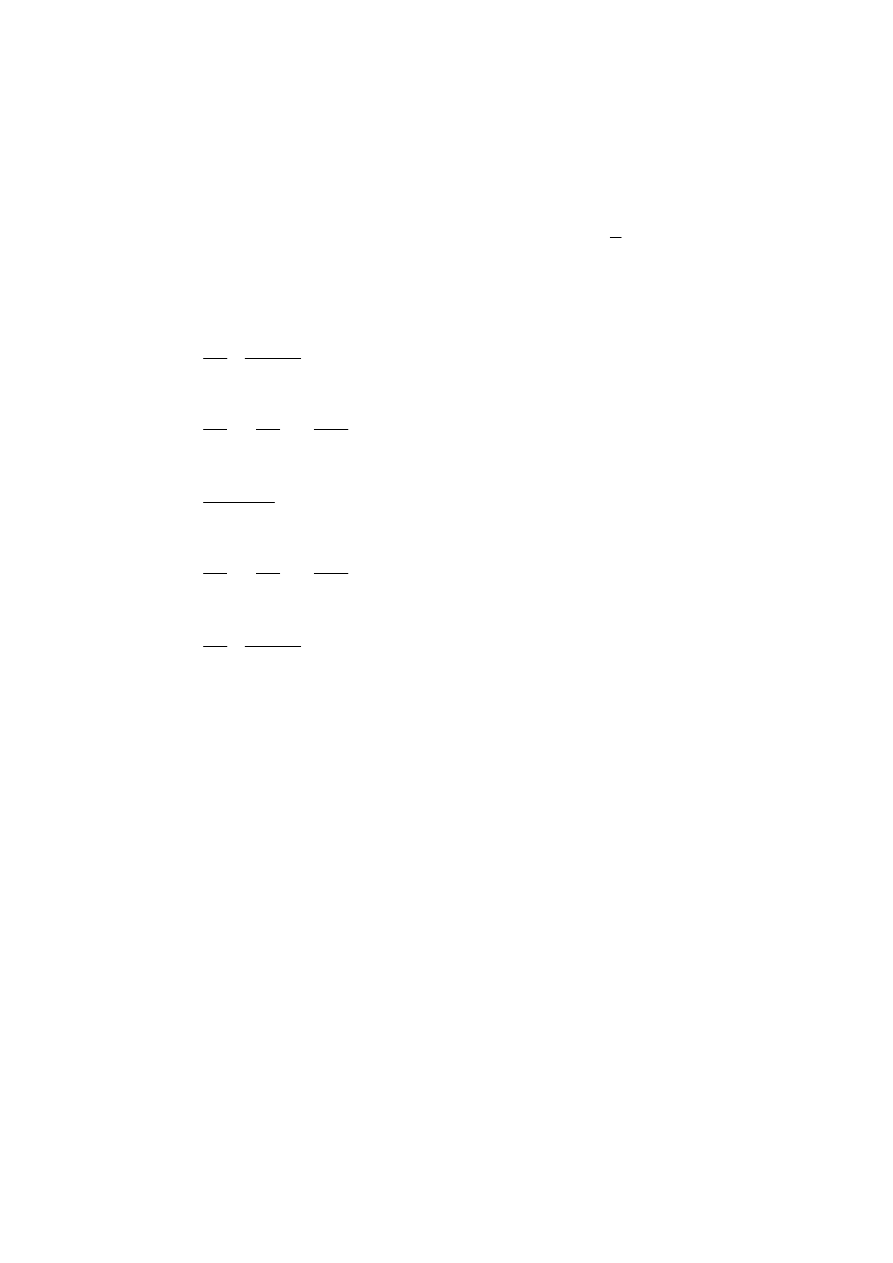
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie
9.
Zmienne losowe
mają jednakową wartość oczekiwaną
n
X
X
X
,
,
,
2
1
K
µ
, jednakową
wariancję
i współczynnik korelacji
2
σ
ρ
=
)
,
(
j
i
X
X
Corr
dla
j
i
≠ . Zmienne losowe
są nawzajem niezależne oraz niezależne od zmiennych losowych
i mają rozkłady postaci
n
Z
,
n
X
,
Z
Z
,
,
2
1
K
X
X
,
,
2
1
K
2
1
=
)
1
=
(
)
0
(
=
=
i
i
Z
P
Z
P
. Oblicz wariancję
zmiennej losowej
.
∑
=
n
i
i
i
X
Z
1
(A)
)
(
4
)
1
(
2
2
2
2
µ
ρσ
σ
−
−
+
n
n
n
(B)
−
+
+
ρ
σ
µ
4
1
1
2
4
2
2
n
n
n
(C)
4
2
2
2
σ
µ
+
n
(D)
−
+
+
ρ
σ
µ
2
1
1
2
4
2
2
n
n
n
(E)
)
(
4
)
1
(
2
2
2
2
µ
ρσ
σ
+
−
+
n
n
n
9
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
Zadanie
10.
Niech
będą niezależnymi zmiennymi losowymi. Zmienne
mają rozkłady wykładnicze o wartości oczekiwanej 1, zmienne losowe
mają rozkłady wykładnicze o wartości oczekiwanej 2. Warunkowy
rozkład zmiennej losowej N przy danym
K
K
,
,
,
,
,
,
,
2
1
2
1
Y
Y
X
X
N
K
,
2
,
1
=
K
,
2
,
1
, i
X
i
,
=
i
Y
i
λ
=
Λ
jest rozkładem Poissona o wartości
oczekiwanej
λ
. Rozkład brzegowy zmiennej
Λ jest rozkładem gamma o gęstości
≤
>
=
−
0
gdy
0
0
gdy
16
)
(
4
λ
λ
λ
λ
λ
e
f
.
Niech
=
>
=
=
>
=
∑
∑
=
=
0
gdy
0
0
gdy
i
0
gdy
0
0
gdy
1
1
N
N
Y
T
N
N
X
S
N
i
i
N
i
i
Oblicz współczynnik korelacji
.
)
,
( T
S
Corr
(A)
0
(B)
15
2
(C)
2
1
(D)
9
4
(E)
9
5
10
Prawdopodobieństwo i statystyka
17.01.2005 r.
___________________________________________________________________________
11
Egzamin dla Aktuariuszy z 17 stycznia 2005 r.
Prawdopodobieństwo i statystyka
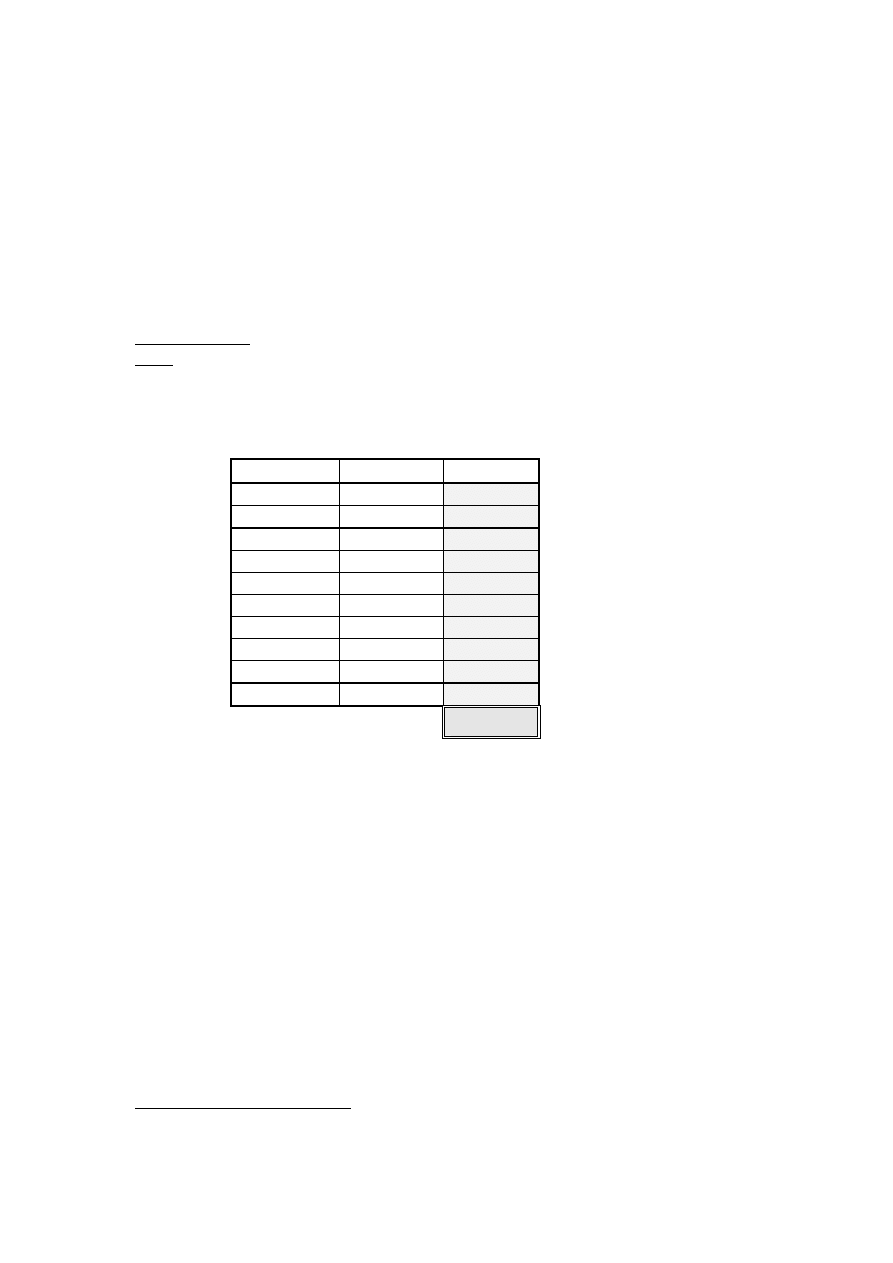
Arkusz odpowiedzi
Imię i nazwisko : ........................... K L U C Z O D P O W I E D Z I ...........................
Pesel ...........................................
Zadanie nr
Odpowiedź Punktacja
1 A
2 A
3 B
4 C
5 D
6 C
7 E
8 A
9 D
10 E
*
Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.
♦
Wypełnia Komisja Egzaminacyjna.