W
Y
T
R
Z
Y
M
A
Ł
O
Ś
Ć
M
A
T
E
R
IA
Ł
Ó
W
–
W
Y
K
Ł
A
D
2
2
2
2
.1
J
e
d
n
o
c
z
e
s
n
e
z
g
in
a
n
ie
i
r
o
z
c
ią
g
a
n
ie
(
lu
b
ś
c
is
k
a
n
ie
)
p
rę
tó
w
p
ro
s
ty
c
h
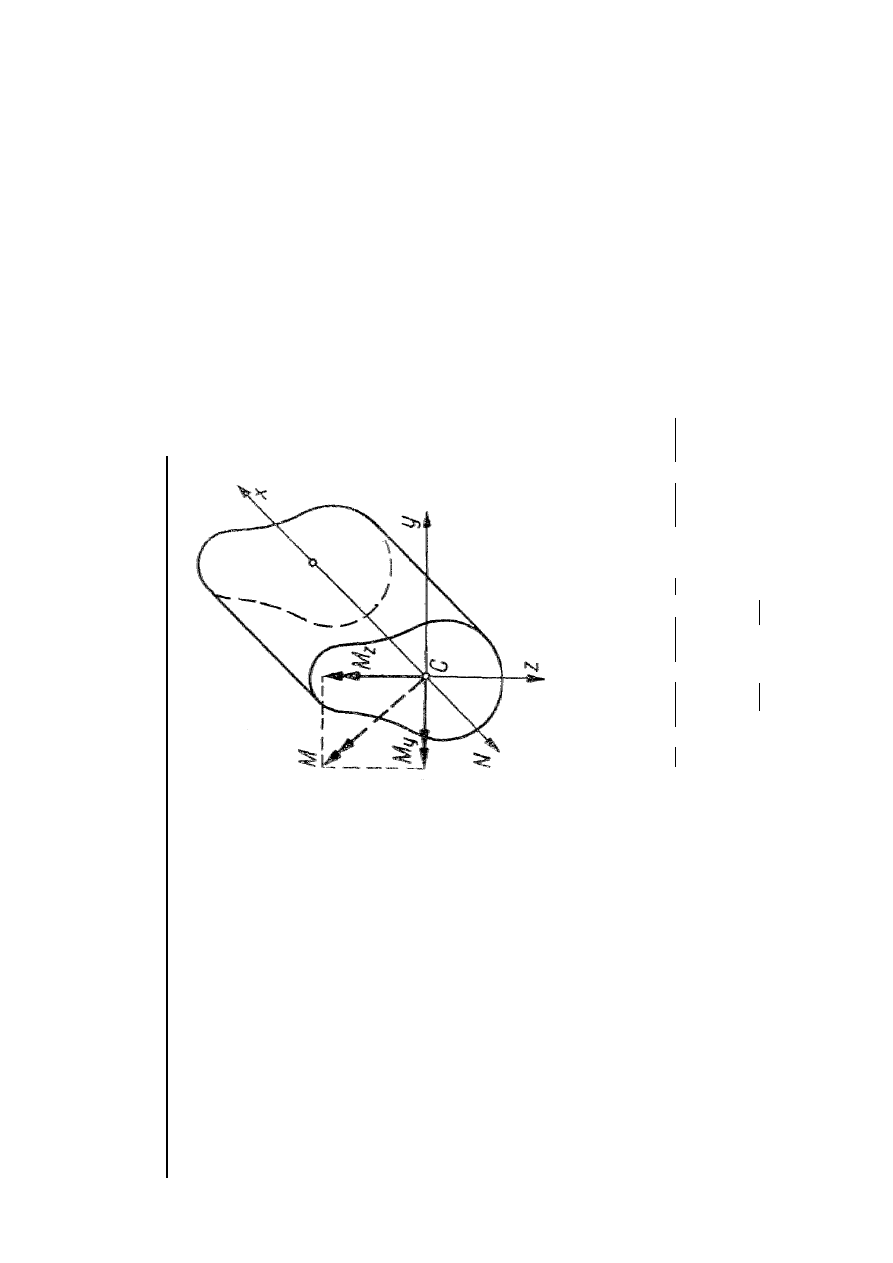
R
y
s
.2
2
.1
P
rę
t
z
g
in
a
n
y
i
r
o
z
c
ią
g
a
n
y
W
z
ó
r
n
a
n
a
p
rę
ż
e
n
ia
n
o
rm
a
ln
e
w
p
rz
y
p
a
d
k
u
p
rę
ta
o
b
c
ią
ż
o
n
e
g
o
j
a
k
n
a
r
y
s
.2
2
.1
−
+
=
−
+
=
2
2
1
z
z
y
y
z
z
y
y
i
y
M
i
z
M
N
A
J
y
M
J
z
M
A
N
σ
(2
2
.1
)
g
d
z
ie
p
ro
m
ie
n
ie
b
e
z
w
ła
d
n
o
ś
c
i
w
z
g
lę
d
e
m
o
s
i
A
J
i
y
y
=
2
,
A
J
i
z
z
=
2
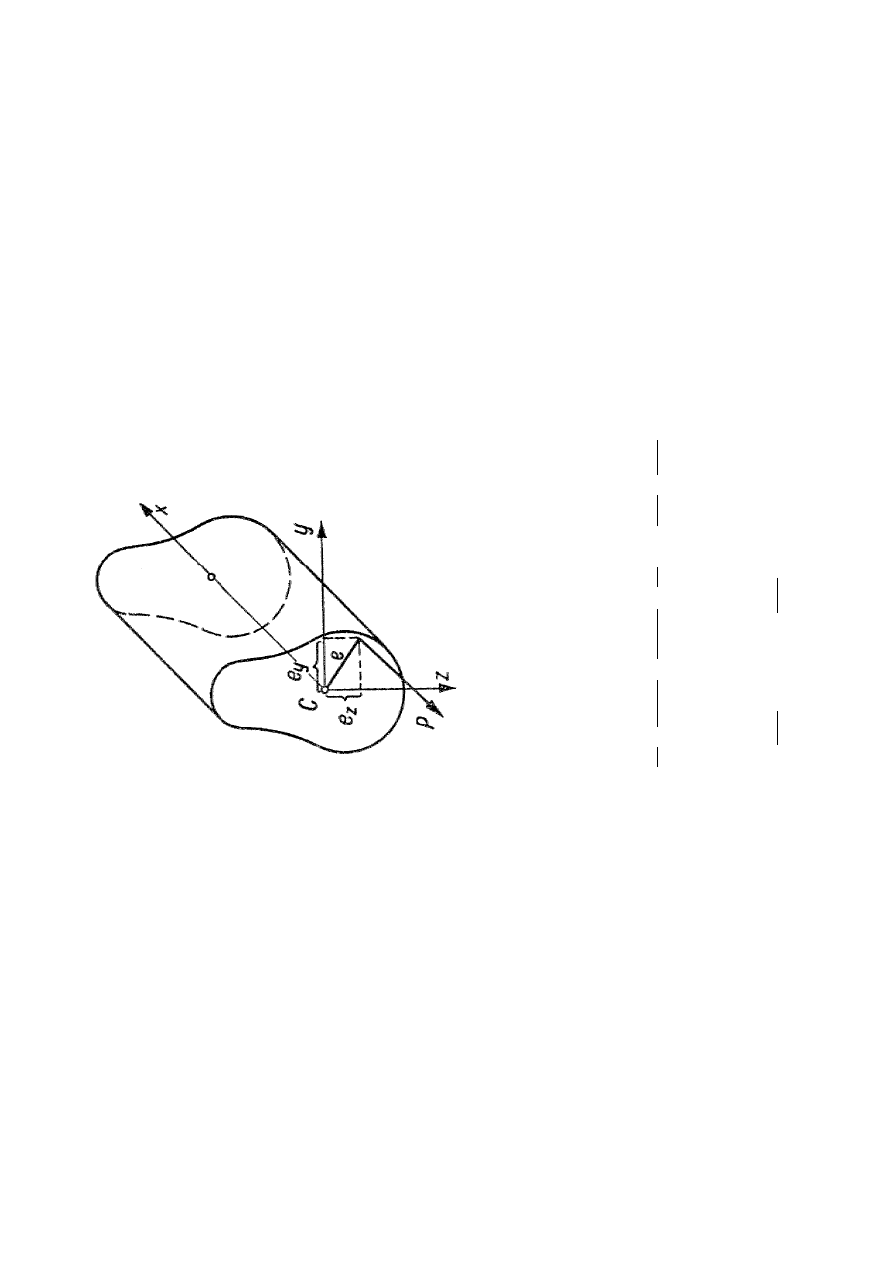
R
y
s
.2
2
.2
P
rz
y
p
a
d
e
k
m
im
o
ś
ro
d
o
w
e
g
o
r
o
z
c
ią
g
a
n
ia
P
rz
e
n
o
s
z
ą
c
s
iłę
P
d
o
ś
ro
d
k
a
c
ię
ż
k
o
ś
c
i
m
o
m
e
n
ty
z
g
in
a
ją
c
e
o
k
re
ś
lo
n
e
s
ą
w
z
o
ra
m
i
z
y
Ne
M
=
,
y
z
Ne
M
−
=
(2
2
.2
)
N
a
p
rę
ż
e
n
ia
n
o
rm
a
ln
e
w
p
rz
e
k
ro
ju
o
k
re
ś
la
z
a
le
ż
n
o
ś
ć
+
+
=
+
+
=
2
2
1
z
y
y
z
z
y
y
z
i
y
e
i
z
e
A
N
J
y
Ne
J
z
Ne
A
N
σ
(2
2
.3
)
J
e
ś
li
o
k
re
ś
lo
n
a
j
e
s
t
s
iła
o
s
io
w
a
i
m
o
m
e
n
ty
z
g
in
a
ją
c
e
t
o
m
o
ż
n
a
o
d
w
ro
tn
ie
o
b
lic
z
y
ć
m
im
o
ś
ro
d
y
N
M
e
z
y
−
=
;
N
M
e
y
z
−
=
(2
2
.4
)
E
k
s
tr
e
m
a
ln
e
n
a
p
rę
ż
e
n
ia
n
o
rm
a
ln
e
w
y
s
tą
p
ią
w
p
u
n
k
ta
c
h
p
rz
e
k
ro
ju
n
a
jb
a
rd
z
ie
j
o
d
d
a
lo
n
y
c
h
o
d
o
s
i
o
b
o
ję
tn
e
j.
P
o
ło
ż
e
n
ie
o
s
i
o
b
o
ję
tn
e
j
m
o
ż
n
a
o
k
re
ś
lić
z
e
w
z
o
ru
(
2
2
.3
)
p
rz
y
ró
w
n
u
ją
c
n
a
p
rę
ż
e
n
ia
d
o
z
e
ra
.
R
ó
w
n
a
n
ie
o
s
i
o
b
o
ję
tn
e
j:
0
1
2
2
=
+
+
z
o
y
y
o
z
i
y
e
i
z
e
(2
2
.5
)
g
d
z
ie
o
o
z
y
,
-
w
s
p
ó
ó
łr
z
ę
d
n
e
p
u
n
k
tó
w
o
s
i
o
b
o
ję
tn
e
j
R
ó
w
n
a
n
ie
o
s
i
o
b
o
ję
tn
e
j
m
o
ż
n
a
t
a
k
ż
e
p
rz
e
d
s
ta
w
ić
w
p
o
s
ta
c
i
ró
w
n
a
n
ia
o
d
c
in
k
o
w
e
g
o
1
2
2
=
−
+
−
z
y
o
y
z
o
e
i
z
e
i
y
(2
2
.6
)
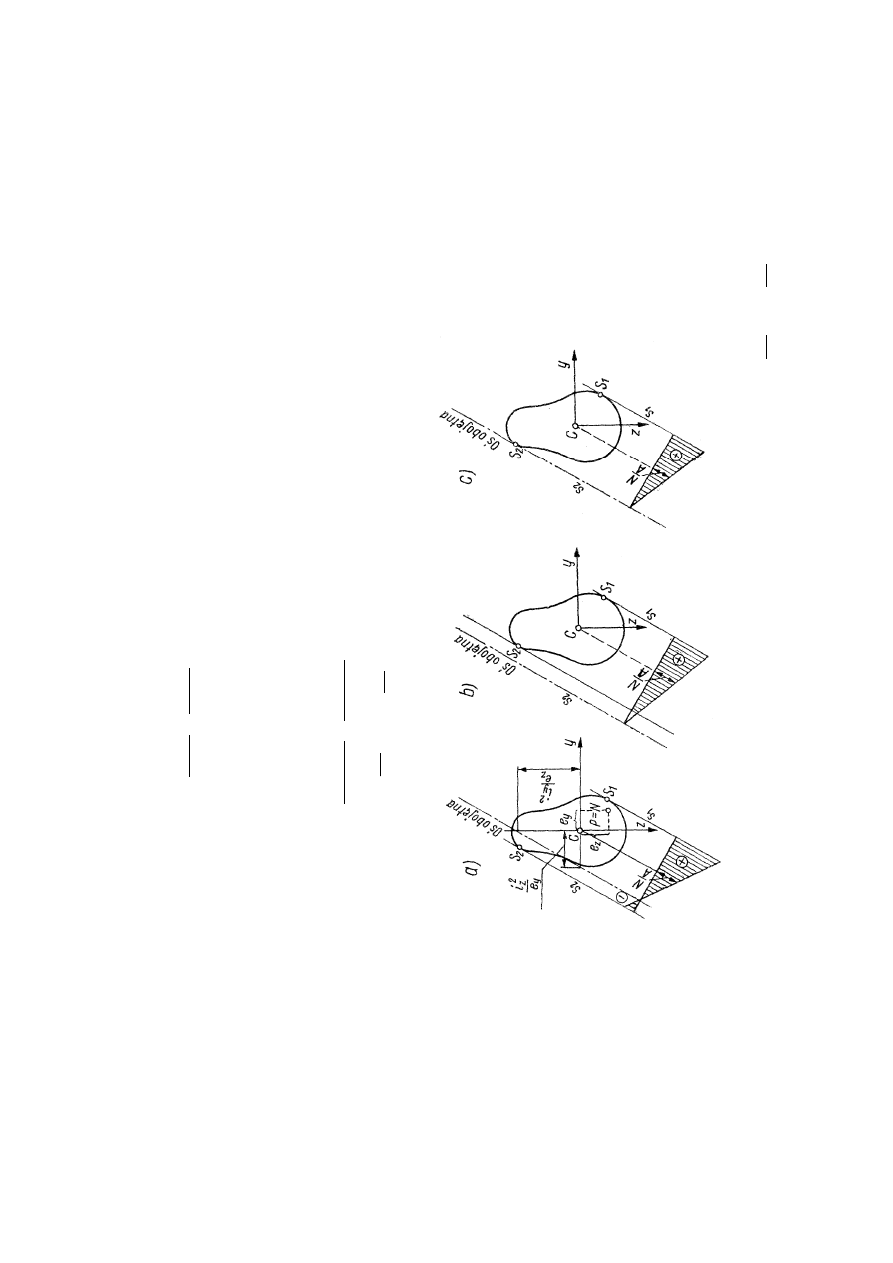
R
y
s
.2
2
.3
P
o
ło
ż
e
n
ie
o
s
i
o
b
o
ję
tn
e
j
w
z
a
le
ż
n
o
ś
c
i
o
d
w
a
rt
o
ś
c
i
w
y
ra
ż
e
ń
−
y
z
e
i
2
,
−
z
y
e
i
2
W
p
rz
e
k
ro
ja
c
h
b
is
y
m
e
tr
y
c
z
n
y
c
h
e
k
s
tr
e
m
a
ln
e
n
a
p
rę
ż
e
n
ia
n
o
rm
a
ln
e
w
y
s
tę
p
u
ją
w
n
a
ro
ż
a
c
h
i
z
b
ę
d
n
e
j
e
s
t
p
o
s
z
u
k
iw
a
n
ie
o
s
i
o
b
o
ję
tn
e
j:
+
±
=
+
±
=
z
y
y
z
z
z
y
y
extr
W
e
W
e
A
N
W
M
W
M
A
N
1
σ
(2
2
.7
)
P
rz
y
k
ła
d
o
w
o
d
la
p
rz
e
k
ro
ju
p
ro
s
to
k
ą
tn
e
g
o
b
ę
d
z
ie
bh
A
=
,
6
2
bh
W
y
=
,
6
2
hb
W
z
=
+
±
=
b
e
h
e
A
N
y
z
extr
6
6
1
σ
(2
2
.8
)
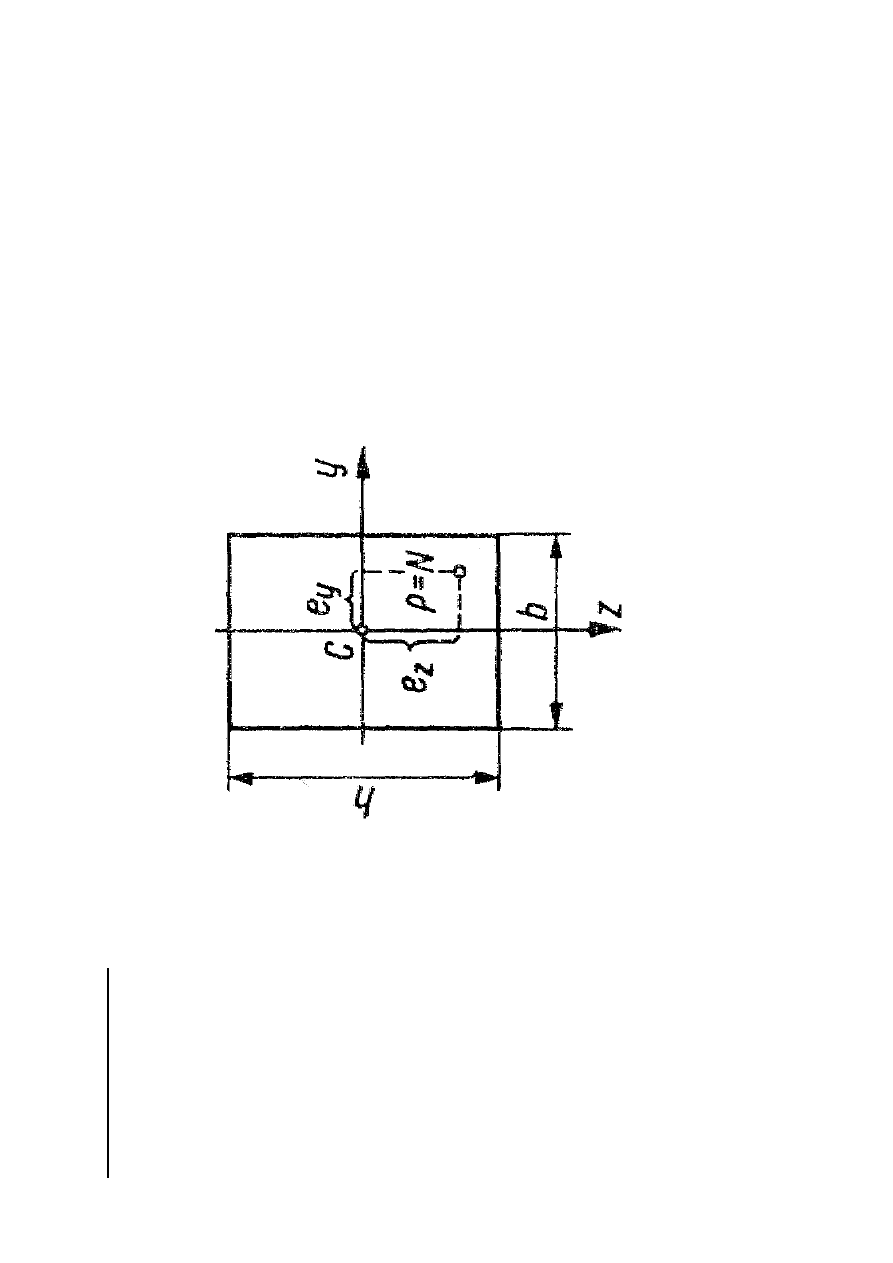
2
2
.2
R
d
z
e
ń
p
rz
e
k
ro
ju
R
d
z
e
n
ie
m
p
rz
e
k
ro
ju
n
a
z
y
w
a
s
ię
m
ie
js
c
e
g
e
o
m
e
tr
y
c
z
n
e
p
u
n
k
tó
w
p
o
ło
ż
e
n
ia
s
iły
P
,
d
z
ia
ła
ją
c
e
j
ró
w
n
o
le
g
le
d
o
o
s
i
p
rę
ta
,
w
y
w
o
łu
ją
c
e
j
n
a
p
rę
ż
e
n
ia
n
o
rm
a
ln
e
j
e
d
n
e
g
o
z
n
a
k
u
R
y
s
.2
2
.4
P
o
ło
ż
e
n
ie
s
iły
P
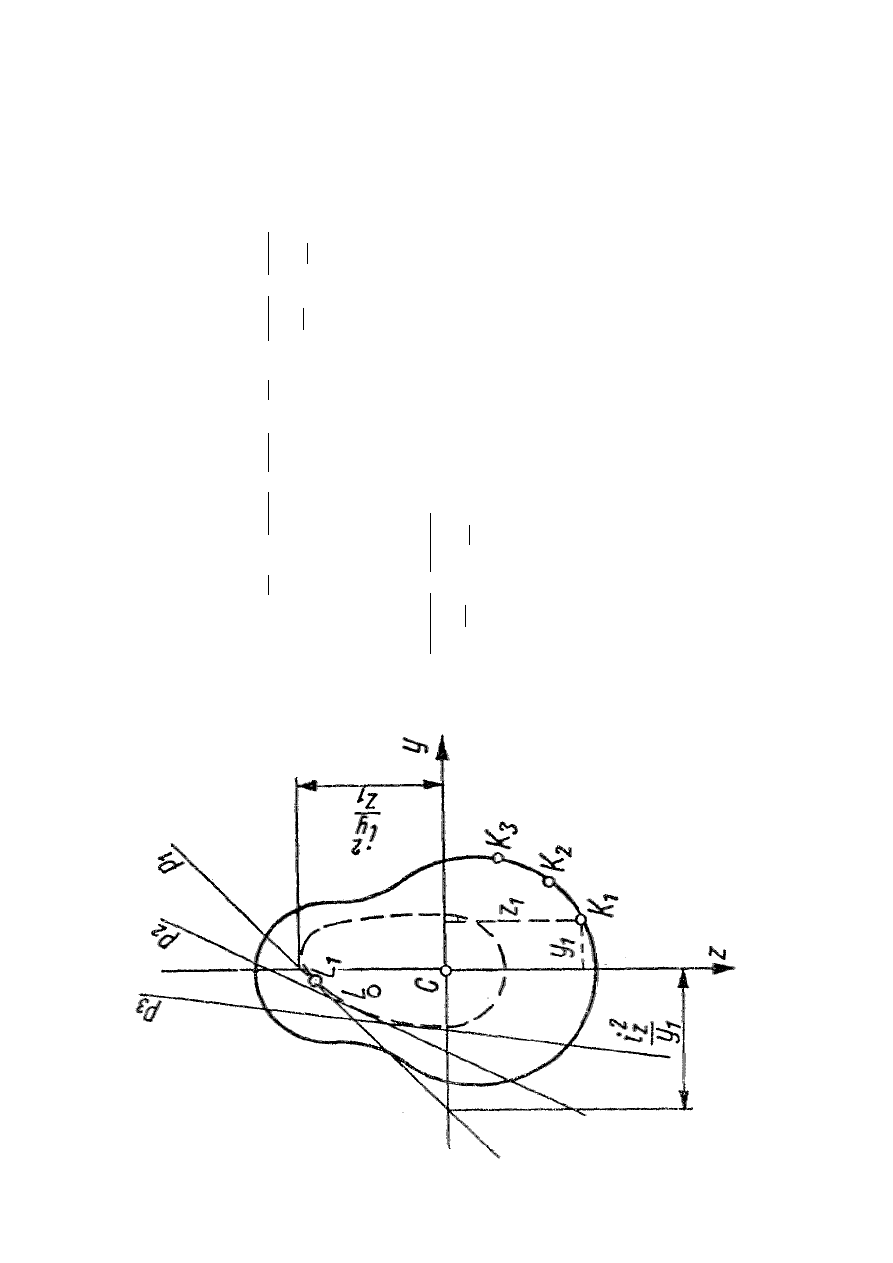
N
a
p
rę
ż
e
n
ie
n
o
rm
a
ln
e
w
p
u
n
k
c
ie
1
K
+
+
=
+
+
=
1
2
1
2
2
1
2
1
1
1
1
z
i
e
y
i
e
A
N
i
z
e
i
y
e
A
N
y
z
z
y
y
z
z
y
K
σ
(2
2
.9
)
M
ie
js
c
e
g
e
o
m
e
tr
y
c
z
n
e
p
u
n
k
tó
w
g
d
z
ie
n
a
p
rę
ż
e
n
ie
0
=
σ
1
1
2
1
1
2
1
=
−
+
−
z
i
e
y
i
e
y
z
z
y
(2
2
.1
0
)
g
d
z
ie
1
1
,
z
y
e
e
-
w
s
p
ó
łr
z
ę
d
n
e
p
u
n
k
tó
w
s
z
u
k
a
n
e
j
lin
ii
–
p
ro
s
ta
1
p
O
b
w
ie
d
n
ia
p
ro
s
ty
c
h
tw
o
rz
y
k
rz
y
w
ą
lu
b
ła
m
a
n
ą
lin
ię
z
a
m
k
n
ię
tą
o
g
ra
n
ic
z
ją
c
ą
r
d
z
e
ń
p
rz
e
k
ro
ju
R
y
s
.2
2
.5
P
o
s
z
u
k
iw
a
n
ie
r
d
z
e
n
ia
p
rz
e
k
ro
ju
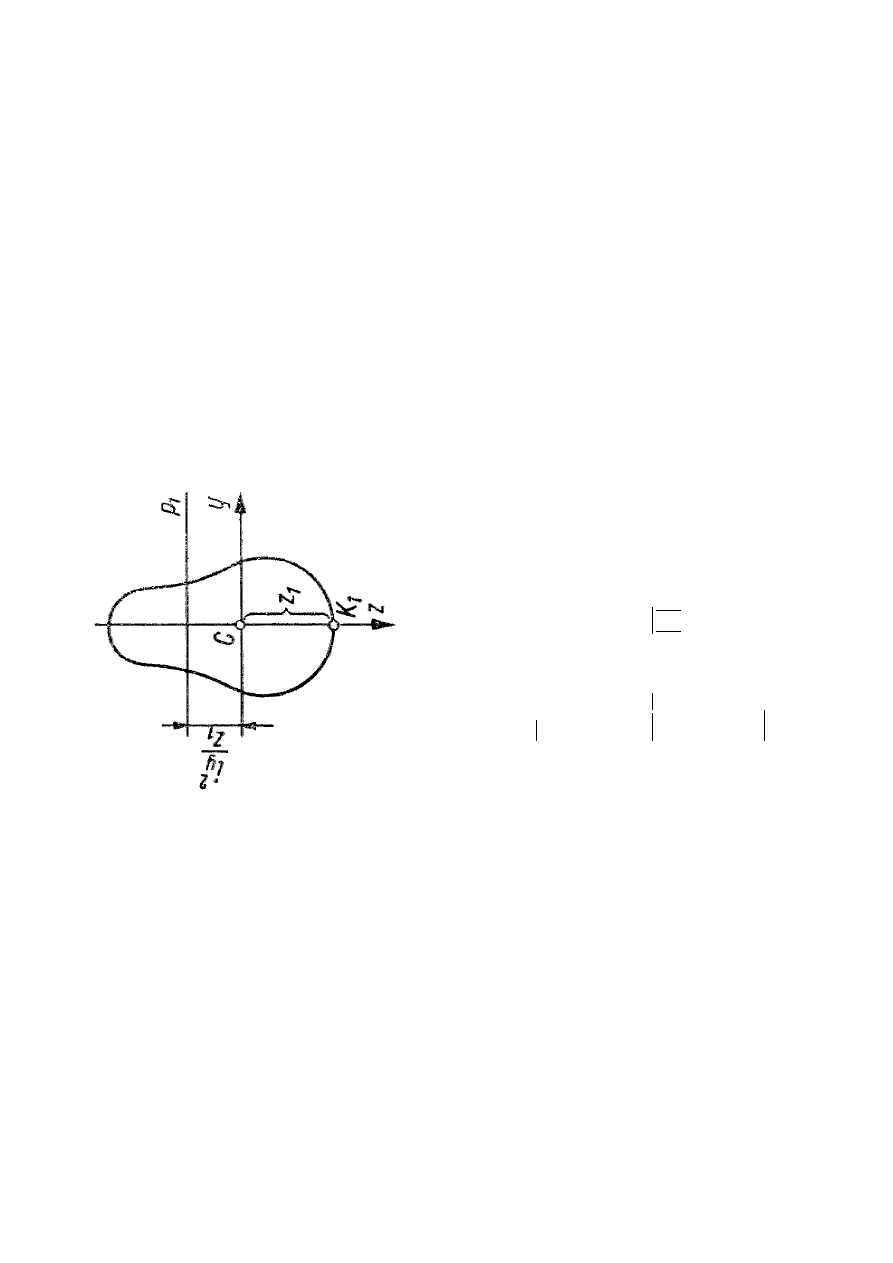
R
y
s
.2
2
.6
S
z
c
z
e
g
ó
ln
y
p
rz
y
p
a
d
e
k
p
o
ło
ż
e
n
ia
p
u
n
k
tu
1
K
J
e
ś
li
p
u
n
k
t
1
K
le
ż
y
n
a
j
e
d
n
e
j
z
o
s
i
g
łó
w
n
y
c
h
w
ó
w
c
z
a
s
1
2
1
z
i
e
y
z
−
=
(2
2
.1
1
)
J
e
ś
li
p
o
n
a
d
to
p
u
n
k
t
1
K
j
e
s
t
n
a
jb
a
rd
z
ie
j
o
d
d
a
lo
n
y
m
p
u
n
k
te
m
p
rz
e
k
ro
ju
b
ę
d
z
ie
A
z
J
e
y
z
1
1
1
−
=
o
ra
z
y
y
W
z
J
=
1
(2
2
.1
2
)
O
s
ta
te
c
z
n
ie
A
W
e
y
z
±
=
1
(2
2
.1
3
)
W
n
io
s
k
i
o
g
ó
ln
e
:
•
J
e
ś
li
k
o
n
tu
r
p
rz
e
k
ro
ju
j
e
s
t
w
ie
lo
b
o
k
ie
m
w
y
p
u
k
ły
m
,
to
i
r
d
z
e
ń
p
rz
e
k
ro
ju
j
e
s
t
w
ie
lo
b
o
k
ie
m
•
K
a
ż
d
e
m
u
w
ie
rz
c
h
o
łk
o
w
i
rd
z
e
n
ia
o
d
p
o
w
ia
d
a
b
o
k
k
o
n
tu
ru
p
rz
e
k
ro
ju
,
a
k
a
ż
d
e
m
u
b
o
k
o
w
i
rd
z
e
n
ia
o
d
p
o
w
ia
d
a
w
ie
rz
c
h
o
łe
k
k
o
n
tu
ru
p
rz
e
k
ro
ju
•
W
p
rz
y
p
a
d
k
u
g
d
y
k
o
n
tu
r
p
rz
e
k
ro
ju
je
s
t
w
ie
lo
b
o
k
ie
m
w
k
lę
s
ły
m
(l
u
b
k
rz
y
w
ą
w
k
lę
s
łą
)
p
rz
y
w
y
z
n
a
c
z
a
n
iu
rd
z
e
n
ia
p
rz
e
k
ro
ju
n
a
le
ż
y
o
b
ie
ra
ć
p
u
n
k
ty
n
a
z
a
s
tę
c
z
y
m
k
o
n
tu
rz
e
p
rz
e
k
ro
ju
b
ę
d
ą
c
y
m
w
ie
lo
b
o
k
ie
m
w
y
p
u
k
ły
m
(
ry
s
.2
2
.7
)
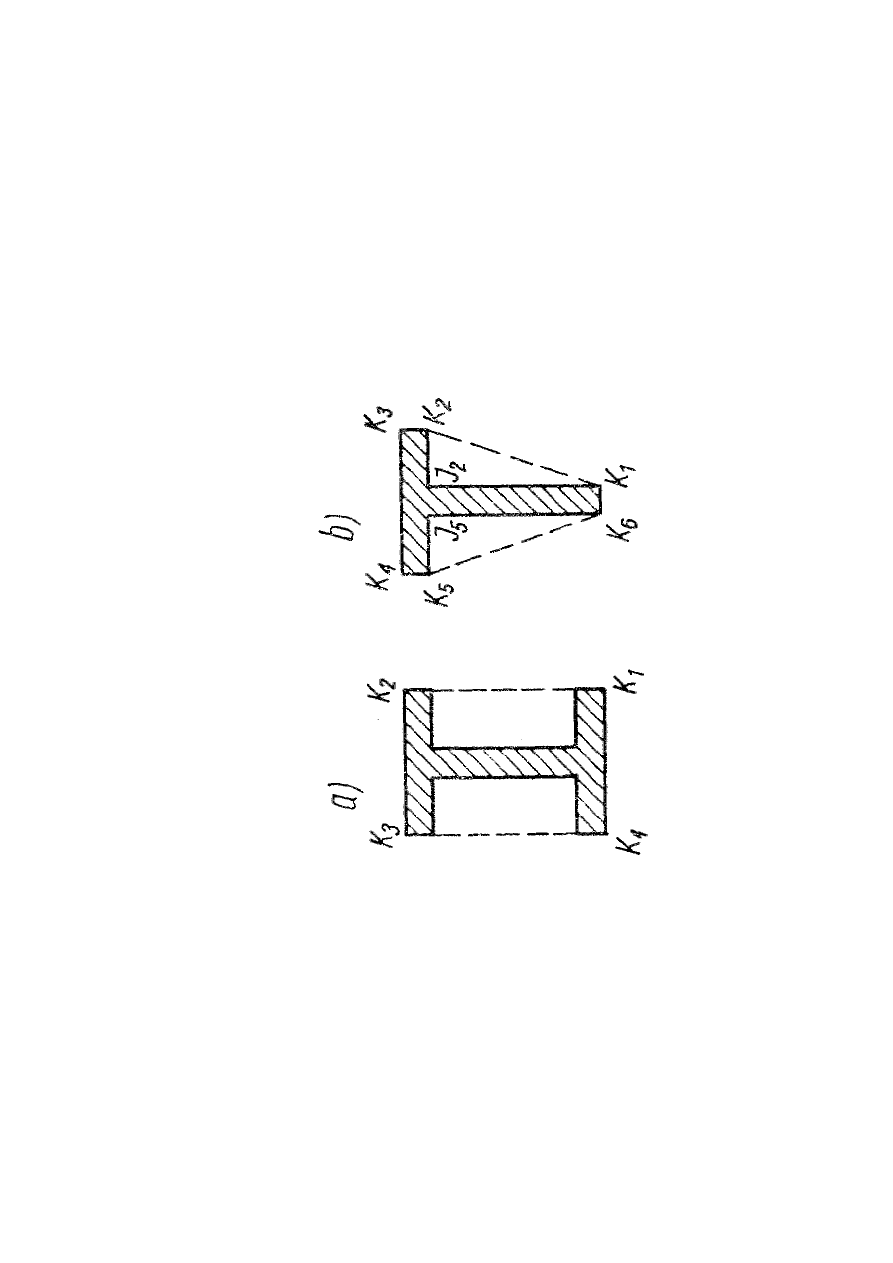
R
y
s
.2
2
.7
Z
a
s
tę
p
c
z
y
k
o
n
tu
r
p
rz
e
k
ro
jó
w
o
k
o
n
tu
rz
e
w
k
lę
s
ły
m
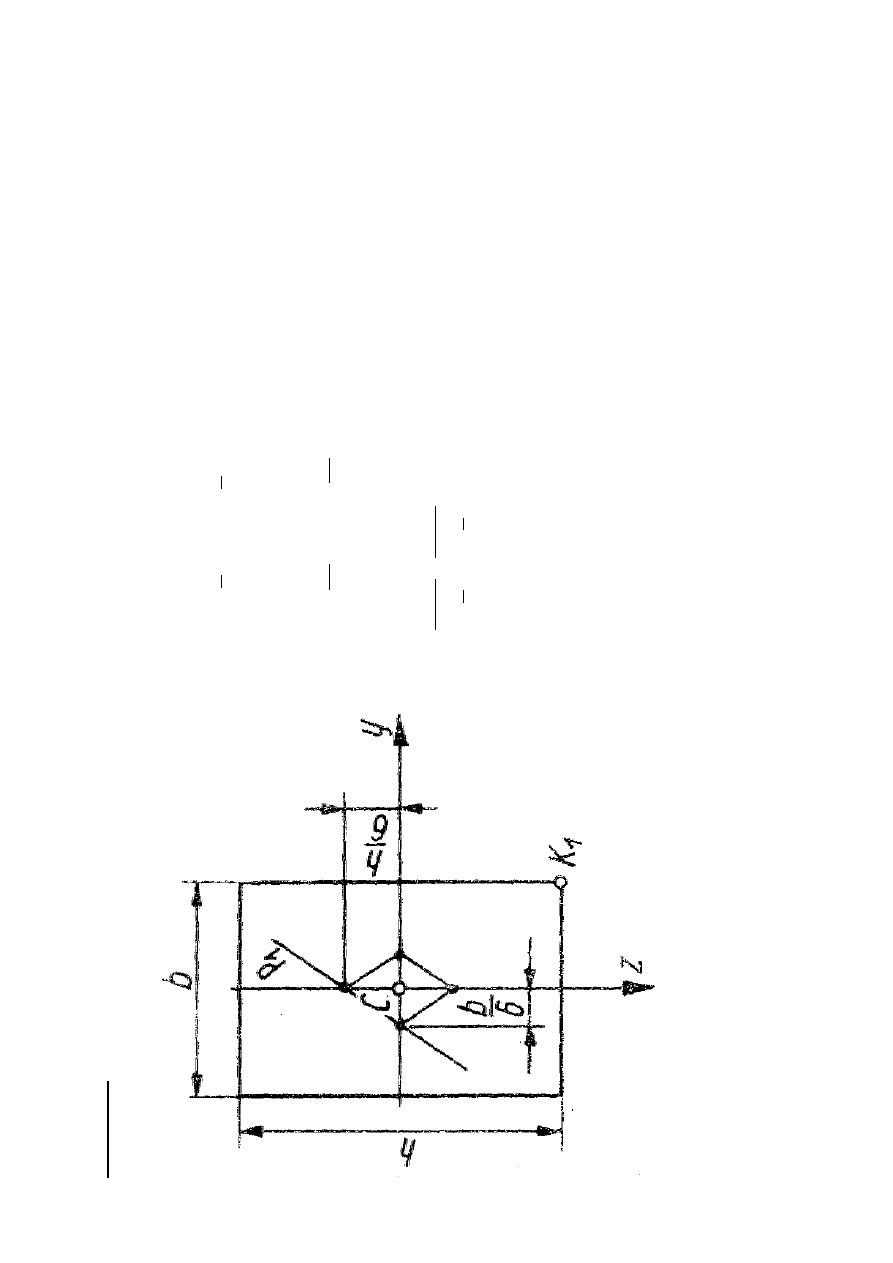
P
rz
y
k
ła
d
y
Z
n
a
le
ź
ć
r
d
z
e
ń
p
rz
e
k
ro
ju
p
ro
s
to
k
ą
tn
e
g
o
W
s
p
ó
łr
z
ę
d
n
e
p
u
n
k
tu
w
j
e
d
n
y
m
z
w
ie
rz
c
h
o
łk
ó
w
2
1
b
y
=
,
2
1
h
z
=
P
ro
m
ie
n
ie
b
e
z
w
ła
d
n
o
ś
c
i
d
la
p
ro
s
to
k
ą
ta
12
2
2
h
i
y
=
,
12
2
2
b
i
z
=
R
ó
w
n
a
n
ie
r
d
z
e
n
ia
1
6
6
1
1
=
−
+
−
h
e
b
e
z
y
J
e
s
t
to
r
ó
w
n
a
n
ie
o
d
c
in
k
o
w
e
p
ro
s
te
j
1
p
Z
u
w
a
g
i
n
a
s
y
m
e
tr
ię
p
rz
e
k
ro
ju
w
z
g
lę
d
e
m
o
b
u
o
s
i
p
o
z
o
s
ta
łe
b
o
k
i
m
o
ż
n
a
w
y
k
re
ś
lić
b
e
z
o
b
lic
z
e
ń
.
R
d
z
e
ń
m
a
k
s
z
ta
łt
r
o
m
b
u
.
R
y
s
.
2
2
.8
R
d
z
e
ń
p
rz
e
k
ro
ju
p
ro
s
to
k
ą
tn
e
g
o
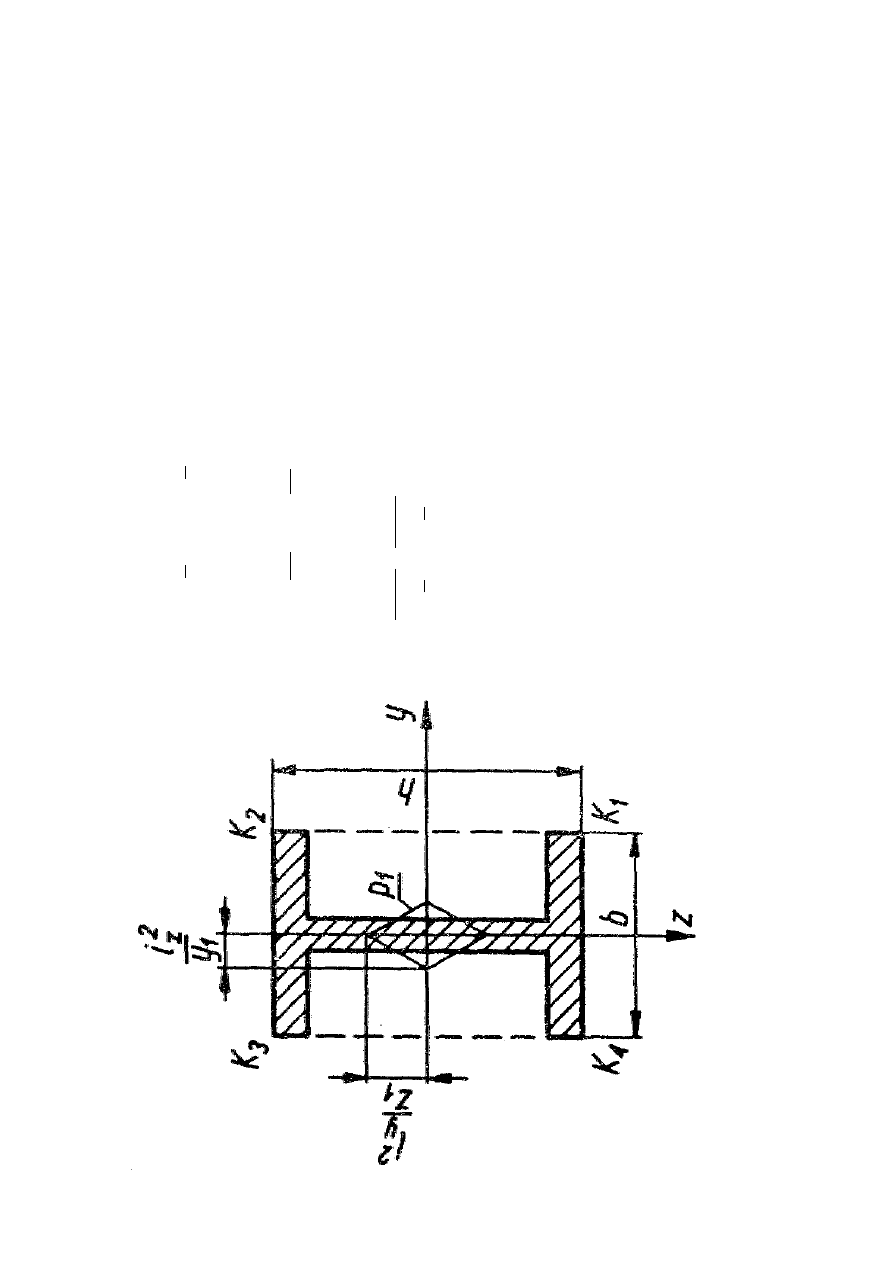
Z
n
a
le
ź
ć
r
d
z
e
ń
p
rz
e
k
ro
ju
d
w
u
te
o
w
e
g
o
W
s
p
ó
łr
z
ę
d
n
e
p
u
n
k
tu
w
j
e
d
n
y
m
z
w
ie
rz
c
h
o
łk
ó
w
2
1
b
y
=
,
2
1
h
z
=
P
ro
m
ie
n
ie
b
e
z
w
ła
d
n
o
ś
c
i
d
w
u
te
o
w
n
ik
a
A
J
i
y
y
=
2
,
A
J
i
z
z
=
2
R
ó
w
n
a
n
ie
r
d
z
e
n
ia
1
6
6
1
1
=
−
+
−
h
e
b
e
z
y
J
e
s
t
to
r
ó
w
n
a
n
ie
o
d
c
in
k
o
w
e
p
ro
s
te
j
1
p
Z
u
w
a
g
i
n
a
s
y
m
e
tr
ię
p
rz
e
k
ro
ju
w
z
g
lę
d
e
m
o
b
u
o
s
i
p
o
z
o
s
ta
łe
b
o
k
i
m
o
ż
n
a
w
y
k
re
ś
lić
b
e
z
o
b
lic
z
e
ń
.
R
d
z
e
ń
m
a
k
s
z
ta
łt
r
o
m
b
u
.
R
y
s
.2
2
.9
R
d
z
e
ń
p
rz
e
k
ro
ju
d
w
u
te
o
w
e
g
o
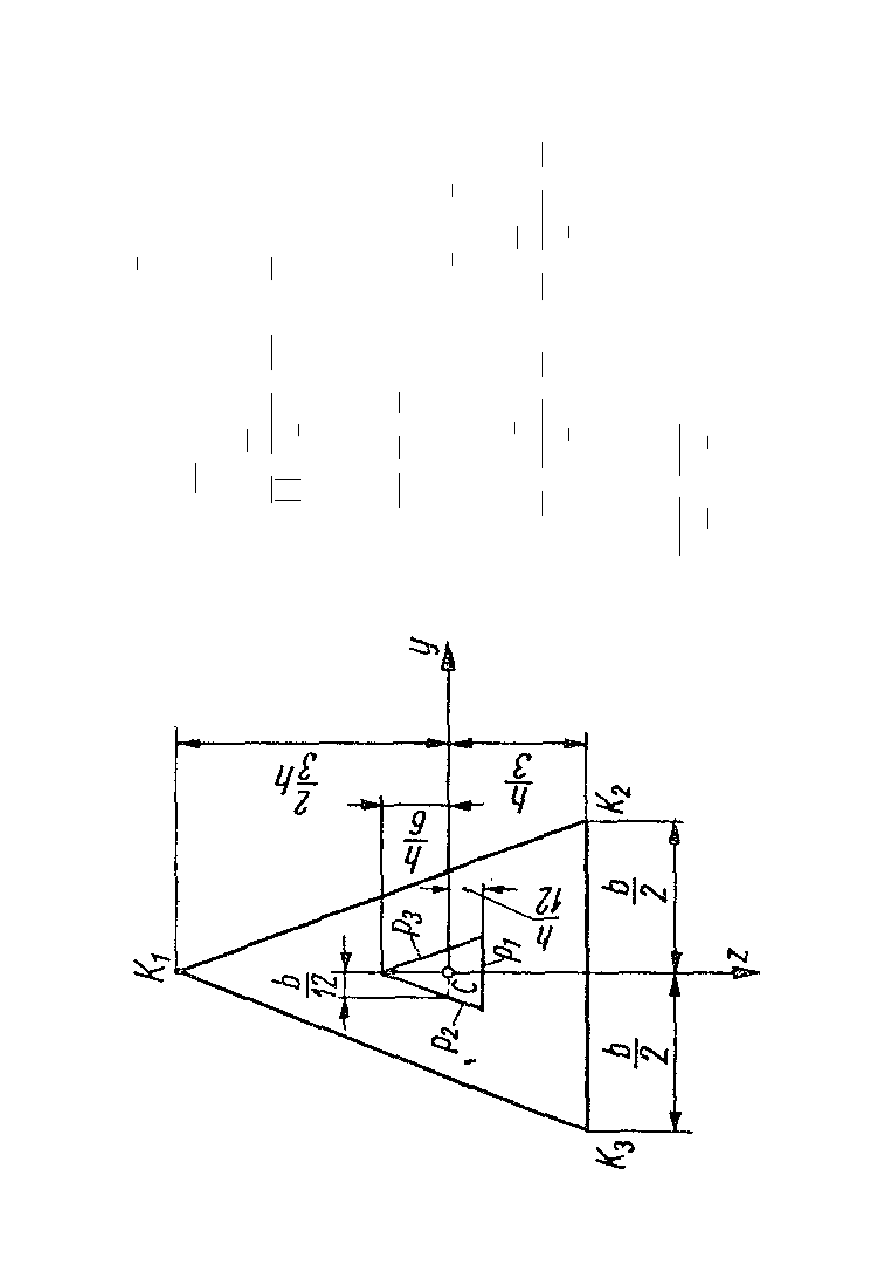
Z
n
a
le
ź
ć
r
d
z
e
ń
p
rz
e
k
ro
ju
o
k
s
z
ta
łc
ie
t
ró
jk
ą
ta
r
ó
w
n
o
ra
m
ie
n
n
e
g
o
D
la
p
u
n
k
tu
1
K
o
w
s
p
ó
łr
z
ę
d
n
e
j
h
z
3
2
1
−
=
b
ę
d
z
ie
A
W
e
y
z
+
=
1
g
d
z
ie
24
3
2
36
1
2
3
1
bh
h
bh
z
J
W
y
y
=
=
=
,
2
bh
A
=
R
ó
w
n
a
n
ie
p
ro
s
te
j
1
p
12
2
:
24
2
1
h
bh
bh
e
z
=
=
D
la
p
u
n
k
tu
2
K
o
w
s
p
ó
łr
z
ę
d
n
y
c
h
2
2
b
y
=
,
3
2
h
z
=
b
ę
d
z
ie
24
2
1
12
2
2
2
3
2
b
bh
b
h
A
J
i
z
z
=
=
=
,
18
2
1
36
1
2
3
2
h
bh
bh
A
J
i
y
y
=
=
=
R
ó
w
n
a
n
ie
p
ro
s
te
j
2
p
1
6
12
2
2
=
−
+
−
h
e
b
e
z
y
R
y
s
.2
2
.1
0
R
d
z
e
ń
p
rz
e
k
ro
ju
t
ró
jk
ą
tn
e
g
o
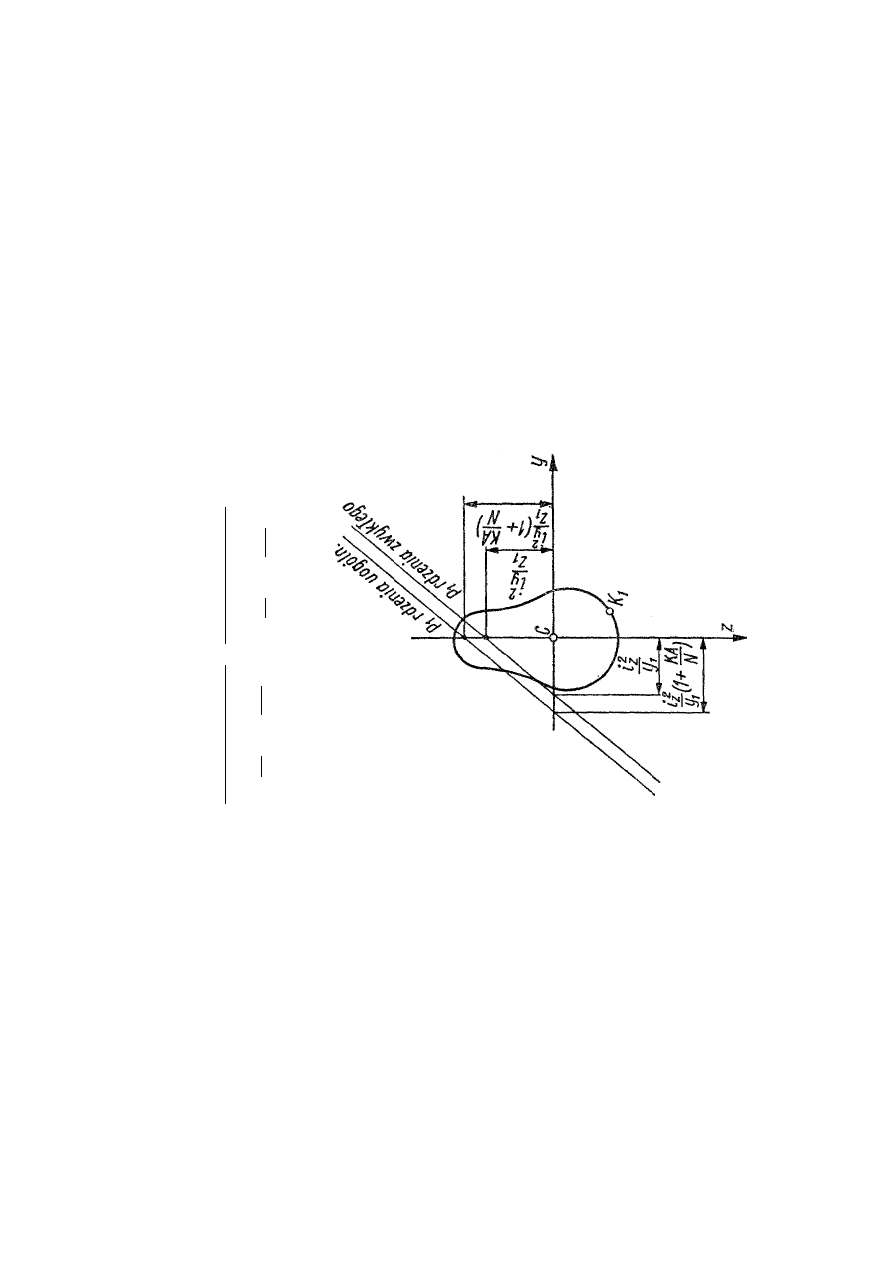
U
o
g
ó
ln
io
n
y
rd
z
e
ń
p
rz
e
k
ro
ju
–
m
ie
js
c
e
g
e
o
m
e
tr
y
c
z
n
e
p
u
n
k
tó
w
p
o
ło
ż
e
n
ia
s
iły
P
,
n
ie
w
y
w
o
łu
ją
c
e
j
n
a
p
rę
ż
e
ń
n
o
rm
a
ln
y
c
h
p
rz
e
c
iw
n
e
g
o
z
n
a
k
u
n
iż
s
iła
P
,
w
ię
k
s
z
y
c
h
o
d
o
k
re
ś
lo
n
e
j
w
a
rt
o
ś
c
i
K
.
R
ó
w
n
a
n
ie
r
d
z
e
n
ia
u
o
g
ó
ln
io
n
e
g
o
1
1
1
1
2
1
2
=
+
−
+
+
−
N
KA
z
i
e
N
KA
y
i
e
y
z
z
y
(2
2
.1
4
)
R
y
s
.2
2
.1
1
O
k
re
ś
la
n
ie
r
d
z
e
n
ia
u
o
g
ó
ln
io
n
e
g
o
Wyszukiwarka
Podobne podstrony:
14 5id 15201 Nieznany (2)
5366 Ref 22 id 41421 Nieznany (2)
08 5id 7231 Nieznany
03 5id 4121 Nieznany
2015 04 09 08 21 22 01id 28638 Nieznany (2)
G2 PB 02 B Rys 3 22 id 185421 Nieznany
2 modul 5id 20554 Nieznany (2)
1 5id 8373 Nieznany (2)
19 5id 18138 Nieznany (2)
05 5id 5463 Nieznany (2)
01 1995 22 26id 3046 Nieznany
IMG 22 id 210963 Nieznany
2 22 stopy niklu Nieznany
22 8id 29427 Nieznany
20 5id 21239 Nieznany (2)
13 5id 14366 Nieznany (2)
Materialy do Wykladu 22 11 13 i Nieznany
06 5id 6114 Nieznany (2)
5id 1085 Nieznany (2)
więcej podobnych podstron