1

Laboratorium z Hydrauliki i Hydrologii – Kierunek Budownictwo inż – sem. V
Politechnika Gdańska
Katedra Hydrotechniki
WILIŚ

Przepływ wody w przewodach zamkniętych (Re+R)

oraz w ośrodku porowatym (Sz)

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z wybranymi zjawiskami hydraulicznymi oraz z

podstawami teoretycznymi i sposobami prowadzenia obliczeń hydraulicznych w przypadku zagadnień
związanych z przepływem wody w rurociągach (przepływ pod ciśnieniem) oraz dla przepływu w
ośrodku porowatym (filtracja).

W ujęciu szczegółowym ćwiczenie ma na celu:

− zapoznanie z pojęciami ruchu laminarnego i turbulentnego oraz znaczeniem liczby Reynoldsa w

obliczeniach hydraulicznych, a także wizualizację obu kategorii ruchów i wyznaczenie krytycznej
wartości liczby Reynoldsa (część I - Re),

− zapoznanie z problemem strat energii mechanicznej przy przepływie pod ciśnieniem w rurociągu

oraz doświadczalne wyznaczenie współczynników oporu dla wybranego fragmentu rurociągu na
stanowisku pomiarowym (część II - R),

− doświadczalne wyznaczenie układu zwierciadła wody przesączającej się przez zaporę ziemną (nasyp

drogi lub linii kolejowej, wał przeciwpowodziowy itp.) przy wykorzystaniu urządzenia
szczelinowego oraz sprawdzenie wpływu uproszczenia polegającego na traktowaniu ruchu
ustalonego płaskiego jako ruchu ustalonego jednowymiarowego (zał. Dupuita) (część III – Sz).

2. Wprowadzenie

Część I. (Re). Ruch laminarny i turbulentny. Liczba Reynoldsa.

W wielu zagadnieniach hydromechaniki i hydrauliki związanych z przepływem cieczy lepkiej,

ważną rolę odgrywa określenie rodzaju ruchu, w jakim znajduje się ciecz. Jedną z podstawowych
klasyfikacji jest podział na ruch laminarny i turbulentny.

W ruchu laminarnym, zwanym także ruchem uwarstwionym, ciecz porusza się wzdłuż

regularnie, płynnie ułożonych warstw (rys. 1a,b), między którymi nie następuje makroskopowe
mieszanie elementów płynu (elementy z poszczególnych warstw nie wykonują ruchów poprzecznych).
Ruch taki możliwy jest przy spełnieniu pewnych warunków, z których podstawowym jest
odpowiednio niska prędkość przepływu. Jeśli jednak prędkość jest dostatecznie duża, elementy płynu

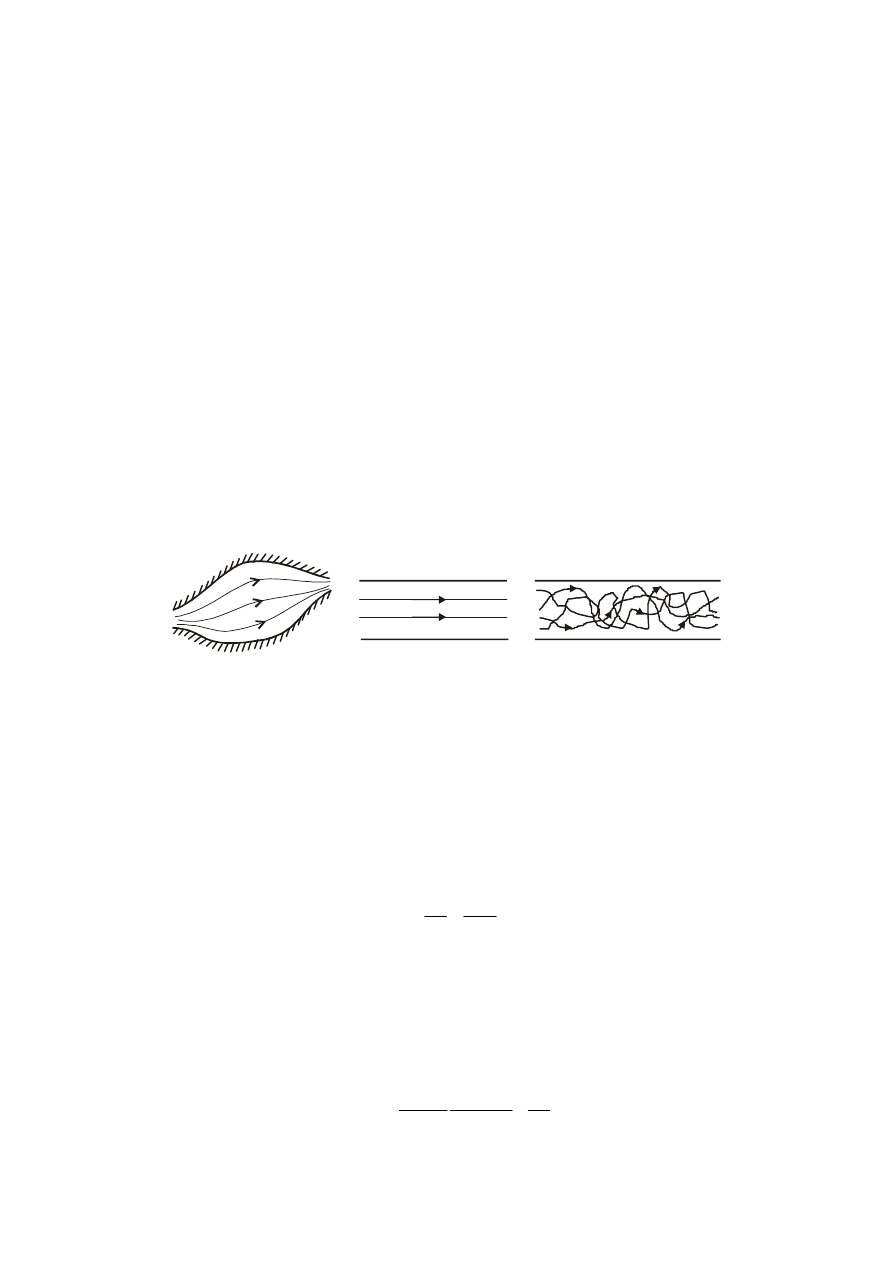
2

oprócz przemieszczenia w głównym kierunku przepływu zaczynają wykonywać również ruchy
poprzeczne, wskutek czego dochodzi do wzajemnego mieszania się warstw cieczy. Te poprzeczne
ruchy cząsteczek nazywane są fluktuacjami turbulentnymi, a ruch określany jest mianem
turbulentnego lub burzliwego (rys. 1c). Znajomość rodzaju ruchu cieczy ma istotne znaczenie
praktyczne. Umożliwia nie tylko jakościowy opis zachowania się elementów cieczy, ale także stanowi
podstawę przy wyborze ogólnej wersji równań ruchu. Z zadań technicznych jako przykład można
podać określanie zależności między wysokością strat energii mechanicznej a prędkością przepływu (w
przypadku ruchu laminarnego wysokość strat jest proporcjonalna do prędkości w potędze pierwszej,
zaś dla ruchu turbulentnego

− w potędze drugiej). Ponadto znajomość rodzaju ruchu umożliwia

między innymi jakościowy opis profilu prędkości w przekroju strumienia oraz szacowanie liczbowej
wartości niektórych współczynników, np. współczynnika de Saint-Venanta.

W przeważającej części zagadnień praktycznych, w przypadku przepływu cieczy w

rurociągach i kanałach otwartych mamy do czynienia z ruchem turbulentnym. Ruch laminarny może
wystąpić tylko przy bardzo małych prędkościach oraz/albo w strumieniach o bardzo małych
wymiarach geometrycznych, rzadko obserwowanych w praktycznych zagadnieniach przepływu pod
ciśnieniem, a jeszcze trudniejszych do zrealizowania w przypadku kanałów otwartych. Natomiast jest
on powszechnie obserwowany podczas przepływu cieczy przez ośrodki porowate.

b) c)

a)

Rys. 1. Układ trajektorii ruchu cząstek w ruchu: a) laminarnym, b) laminarnym w przewodzie

o ściankach równoległych, c) turbulentnym w przewodzie o ściankach równoległych

Pojęcie liczby Reynoldsa. Krytyczna liczba Reynoldsa

Kryterium umożliwiającym określenie rodzaju ruchu cieczy jest tzw. liczba Reynoldsa (Re),

będąca bezwymiarowym wyrażeniem postaci

µ

ρ

ν

UL

UL

Re

=

=

(1)

w którym U jest prędkością reprezentatywną (charakterystyczną, typową, przeciętną) dla badanego
zjawiska, L jest reprezentatywnym wymiarem liniowym,

ρ

jest gęstością cieczy, zaś

ν

oraz

µ

są

odpowiednio kinematycznym i dynamicznym współczynnikiem lepkości, przy czym

µ

=

ρ ν

.

Zarówno

ρ

jak i

µ

zależne są od temperatury i dla wody o temperaturze z zakresu 0 – 40

0

C mogą być

wyznaczone ze wzorów:

(

)

⎥⎦

⎤

⎢⎣

⎡

+

+

−

−

=

3

2

)

2

.

67

(

)

283

(

57

.

503

4

1000

m

kg

t

t

t

ρ

(2)

3

oraz

⎥⎦

⎤

⎢⎣

⎡ ⋅

+

+

=

2

2

000221

.

0

0337

.

0

1

m

s

N

t

t

o

µ

µ

(3)

gdzie t – jest temperaturą w

o

C, zaś

µ

o

jest dynamicznym współczynnikiem lepkości dla temperatury

0

o

C, który dla wody wynosi

µ

o

= 0.00179 [N s/m

2

].

Dla przepływu pod ciśnieniem w rurociągu o przekroju kołowym za L przyjmuje się średnicę

rurociągu d, zaś U jest równe średniej prędkości w przekroju poprzecznym rurociągu v:

µ

ρ

ν

d

d

v

v

Re

=

=

(4)

Liczba Reynoldsa określa stosunek sił bezwładności do sił lepkości (sił tarcia wewnętrznego

cieczy). Im większa jest jej wartość, tym siły lepkości odgrywają mniejszą rolę w ruchu cieczy, a
cząsteczki mogą łatwiej przemieszczać się w kierunkach poprzecznych do głównego kierunku
przepływu. Ogólnie, jeśli Re jest mniejsza od pewnej wartości granicznej to ruch jest laminarny,
natomiast w przeciwnym przypadku ruch jest turbulentny. Ta graniczna wartość liczby Re, przy
której ruch zmienia charakter z laminarnego w turbulentny lub odwrotnie, nosi nazwę krytycznej
liczby Reynoldsa

(Re

kr

). Należy zwrócić uwagę, że krytyczna liczba Reynoldsa przyjmuje różne

wartości w zależności od rodzaju badanego zjawiska. Przejście z ruchu laminarnego w turbulentny
realizuje się przy innej wartości wyrażenia w przypadku przepływów w rurociągu, przy innej dla
przepływu w kanałach i jeszcze innej dla przepływu cieczy w ośrodku porowatym.

W przypadku rurociągów wykazano doświadczalnie (doświadczenie Osborne’a Reynoldsa,

1883 r.), że przejście z ruchu laminarnego w turbulentny może wystąpić w relatywnie szerokim
zakresie liczb Re. Najmniejszą wartością Re, określoną wg (4), przy której można zaobserwować to
przejście jest wartość 2320. Jest to tzw. dolna krytyczna liczba Reynoldsa (Re

kr d

). Poniżej tej wartości

zawsze

obserwuje się ruch laminarny. Jeśli jednak prędkość cieczy poruszającej się początkowo

ruchem laminarnym będzie stopniowo wzrastała w sposób bardzo delikatny (łagodny), a w czasie
trwania eksperymentu nie wystąpią nawet drobne zewnętrzne zakłócenia, przejście z ruchu laminarnego
w turbulentny może nastąpić później, przy większej wartości liczby Reynoldsa. Maksymalna wartość
liczby Reynoldsa, przy której może nastąpić przejście z ruchu laminarnego w turbulentny nosi nazwę
górnej krytycznej liczby Reynoldsa (

Re

kr g

) (rys. 2) i wynosi ok. 50000. Strefa pomiędzy wartościami

Re

kr d

= 2320 a Re

kr g

= 50000 nosi nazwę strefy przejściowej. W praktyce jednak zaledwie niewielkie

zakłócenie zewnętrzne w strefie przejściowej powoduje utratę laminarnego charakteru przepływu, a raz
wytworzony ruch turbulentny przy liczbach Reynoldsa większych niż 2320 utrzymuje się już w sposób
trwały.

Z kolei jeśli doświadczenie prowadzone jest w sposób odwrotny, to znaczy następuje

stopniowe zmniejszanie prędkości przepływu, a co za tym idzie

− wartości liczby Re, począwszy od

poziomu przekraczającego 50000 aż do liczb mniejszych niż 2320, obserwacje dowodzą, że dla
wartości liczb Re powyżej 2320 nie można zaobserwować ruchu laminarnego, nawet jeśli występował
on przy tej wartości Re przy zwiększaniu prędkości przepływu. Potwierdza to poprzednie
stwierdzenie, że powyżej wartości Re = 2320 raz wywołany ruch turbulentny nie może już przejść w
ruch laminarny. Dopiero przy Re = 2320 następuje przejście w ruch laminarny, który utrzymuje się

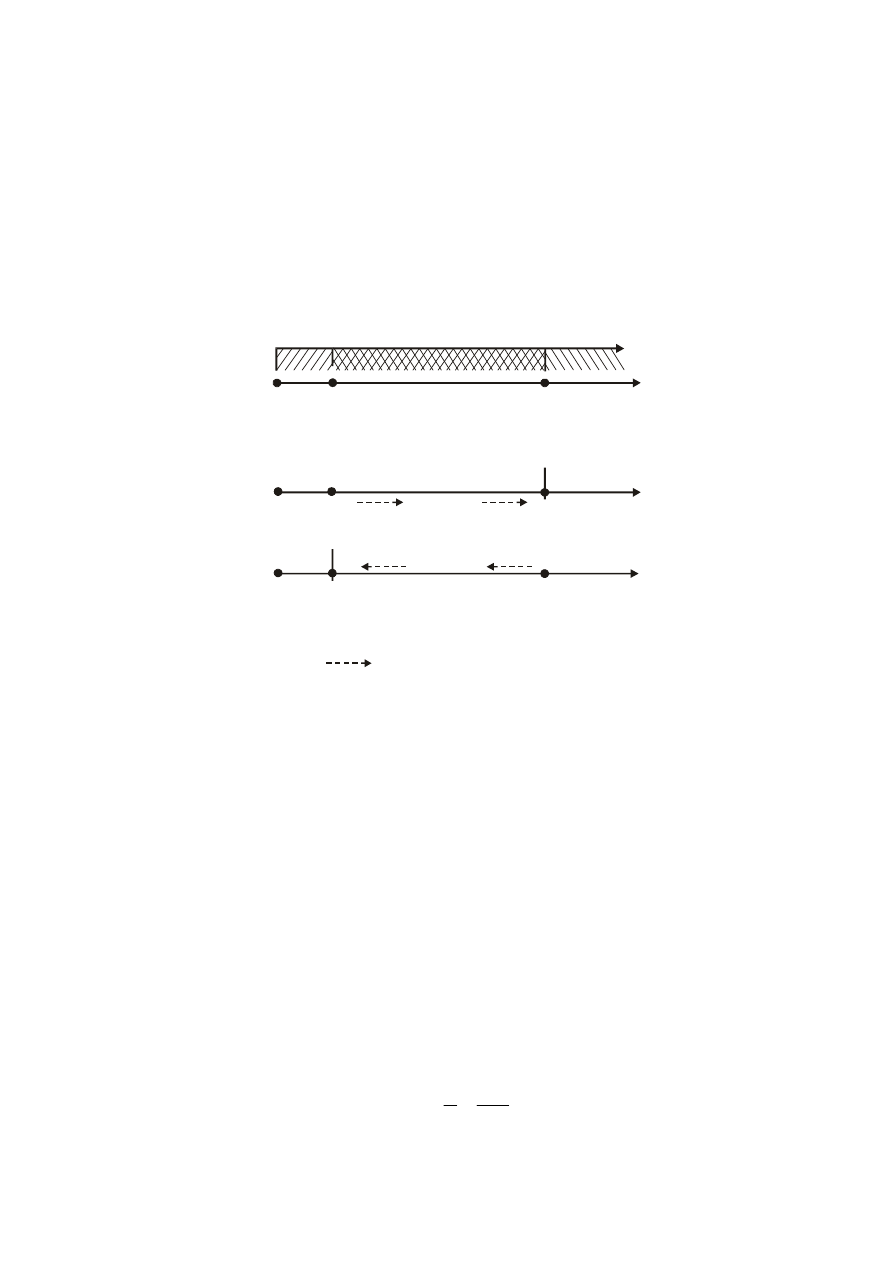
4

także poniżej tej wartości liczby Reynoldsa. Wpływ sposobu prowadzenia doświadczenia na rodzaj
ruchu obserwowanego w strefie przejściowej przedstawia rys. 2b.
Ze względu na fakt, że ruch laminarny w strefie przejściowej jest niestabilny, w przypadkach
praktycznych za ostateczną wartość krytycznej liczby Reynoldsa przyjmuje się 2320. W pierwszej
części ćwiczenia laboratoryjnego dąży się do powtórzenia obserwacji przeprowadzonych przez
Reynoldsa i wyznaczenia wartości krytycznej Re dla przepływu pod ciśnieniem w przewodzie o
przekroju kołowym.

strefa ruchu
laminarnego

strefa przejściowa

strefa ruchu
turbulentnego

~50 000

wartość Re

Re

kr g

Re

kr d

0 ~2300

a)

Re

kr d

Re

kr d

Re

kr g

Re

kr g

b)

ruch
laminarny

ruch laminarny

ruch turbulentny

ruch turbulentny

wartość Re

wartość Re

kierunek prowadzenia doświadczenia

Rys. 2. Interpretacja dolnej i górnej krytycznej liczby Reynoldsa:

a) strefy występowania ruchu laminarnego i turbulentnego; b) przejście z ruchu

laminarnego w turbulentny i odwrotnie

Część II. (R). Opory ruchu w rurociągach

Przy obliczeniach hydraulicznych przewodów pod ciśnieniem najczęściej stosuje się

układ równań złożony z równania ciągłości:

Q

= v F = const.

(5)

oraz równania Bernoulliego.

Miarą energii mechanicznej strumienia przepływającej cieczy jest wartość tzw. trójmianu

Bernoulliego:

g

p

z

B

2

2

v

α

γ

+

+

=

(6)

5

w którym B jest wartością energii mechanicznej wyrażonej w jednostkach wysokości słupa cieczy, z
jest wzniesieniem środka ciężkości przekroju poprzecznego strumienia ponad przyjętym poziomem
porównawczym, p jest ciśnieniem, v – średnią prędkością strumienia, a

α

jest tzw. współczynnikiem

de Saint Venanta.

Równanie Bernoulliego, określające przemiany energetyczne przy przepływie cieczy przez

przewód zamknięty, dla wybranego odcinka przewodu, ograniczonego przekrojami 1 i 2 przyjmuje
postać:

B

1

= B

2

+ h

str 1-2

(7a)

czyli:

2

1

2

2

2

2

2

2

1

1

1

1

2

2

−

+

+

+

=

+

+

str

h

g

p

z

g

p

z

v

v

α

γ

α

γ

(7b)

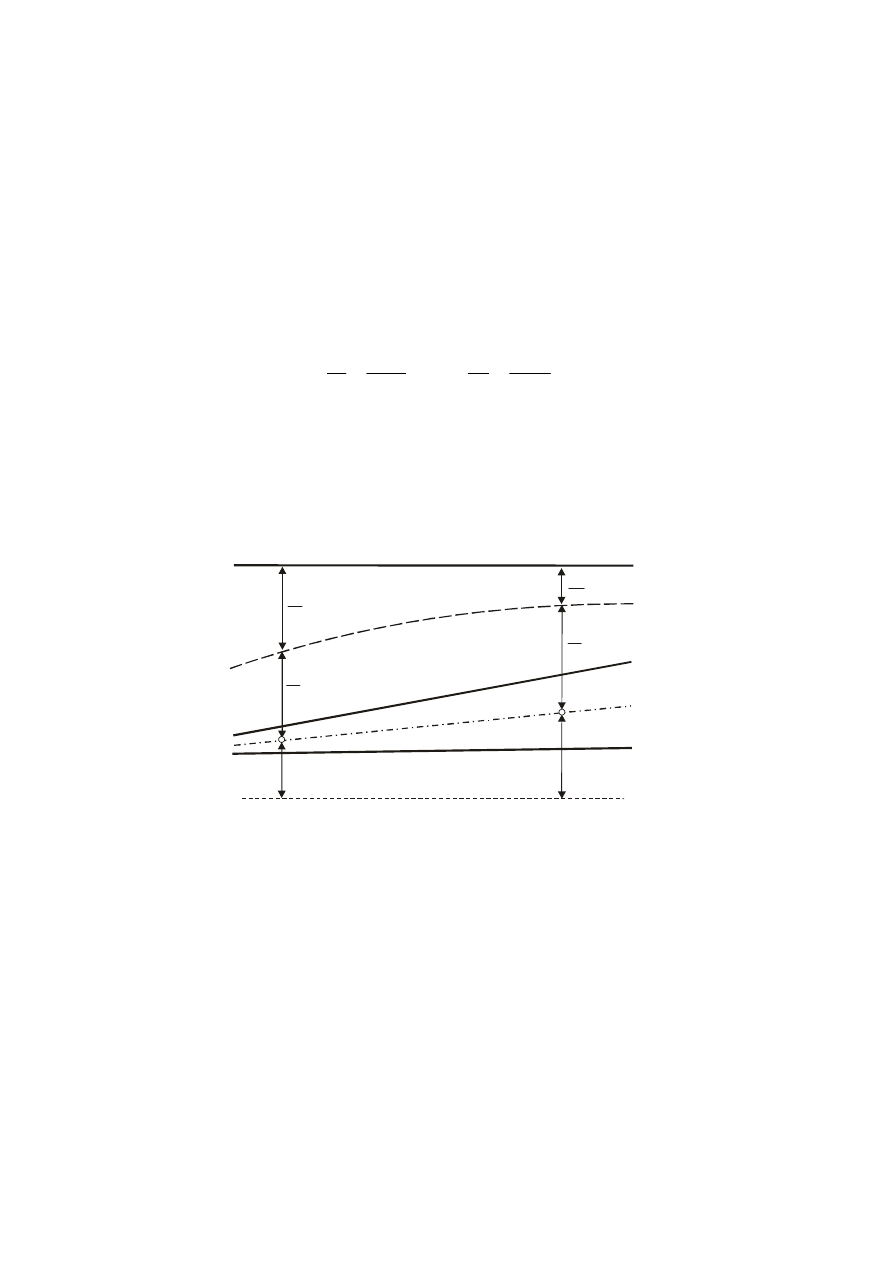
Oznacza to, że w trakcie przepływu cieczy możliwe są wzajemne przemiany form energii
mechanicznej – potencjalnej w kinetyczną i odwrotnie (np. na skutek zmiany geometrii przewodu), a
ponadto część energii mechanicznej cieczy jest tracona na pokonanie oporów tarcia przy przepływie,
co określane jest stratami energii mechanicznej lub stratami hydraulicznymi h

str

(rys. 3).

linia energii
dla cieczy nielepkiej

linia ciśnienia

v
2g

2

1

poziom porównawczy

p

g

ρ

p

g

ρ

1

2

1

2

v

2g

2

2

z

1

z

2

Rys. 3. Interpretacja graficzna równania Bernoulliego dla cieczy nielepkiej.

Wśród strat energii mechanicznej wyróżnia się straty na długości, zwane też stratami

liniowymi

(spowodowane tarciem wewnętrznym cieczy wzdłuż odcinków o regularnym przebiegu

linii prądu, głównie w pobliżu ścianek) oraz straty miejscowe lub inaczej lokalne (spowodowane
tarciem wewnętrznym cieczy wzdłuż odcinków o nieregularnym, skomplikowanym przebiegu linii
prądu, co z reguły wywołane jest przez lokalnie umieszczone przeszkody, np. zawory, kolanka itp.).

Straty na długości

Wysokość liniowych strat energii przy przepływie zależna jest od szeregu czynników, przede

wszystkim od rodzaju przepływającej cieczy, prędkości jej przepływu, rodzaju ruchu panującego w
przewodzie (ruch laminarny lub turbulentny), geometrii przewodu (długości przewodu, kształtu i
wymiarów przekroju poprzecznego) oraz chropowatości wewnętrznej powierzchni rury. Najczęściej

6

stosowanym wzorem umożliwiającym określenie wysokości strat energii w przewodzie kołowym o
stałej średnicy d i długości L jest formuła Darcy’ego-Weisbacha:

g

d

L

h

str

2

2

v

λ

=

(8)

w której v jest średnią prędkością przepływu strumienia, g – przyspieszeniem ziemskim, zaś

λ

jest

współczynnikiem oporów liniowych

, uwzględniającym wpływ pozostałych czynników na wysokość

strat energii. Warto podkreślić, że wzór Darcy’ego-Weisbacha nie jest jedynym wzorem, jaki określa
opory na długości, jednakże w przypadku przepływu cieczy pod ciśnieniem jest niewątpliwie jednym
z najczęściej stosowanych.

Podstawowym problemem związanym z zastosowaniem formuły (8) do wyznaczenia

wysokości strat liniowych jest poprawne określenie wartości współczynnika oporów liniowych

λ

,

który – jak już wspomniano – uwzględnia wpływ rodzaju ruchu i chropowatości materiału przewodu
na wysokość strat energii.

Z technicznego punktu widzenia każdy materiał, z którego wykonany jest przewód, wykazuje

pewną chropowatość. Zależy ona nie tylko od wysokości nierówności na ściance, czyli wzniesień i
wgłębień na wewnętrznej powierzchni rury, ale także od kształtu i rozmieszczenia tych nierówności.
Jest więc ona związana zarówno z rodzajem materiału jak i stopniem jego zużycia (np. korozja
przewodów). Za miarę chropowatości przyjmuje się pewną wartość k (wyrażaną w milimetrach), która
określa średnią wysokość nierówności na powierzchni przewodu, z uwzględnieniem
nierównomierności ich rozmieszczenia. Wielkość k nazywana jest chropowatością bezwzględną.
Orientacyjne jej wartości można znaleźć w odpowiednich tabelach. Przykładowo, dla nowych rur
stalowych k może być mniejsze od 0,1 mm, podczas gdy dla skorodowanych rur żeliwnych z
inkrustacjami może osiągać wartość nawet do 3 mm. W przypadku rur wykonanych z nowych
materiałów (np. kolejnych odmian tworzyw sztucznych), szacunkowa wartość k powinna być
podawana przez ich producenta.

Jak wykazała praktyka, w przypadku przepływu cieczy chropowatość bezwzględna nie jest

wystarczającą miarą, umożliwiającą ocenę wpływu rodzaju materiału na parametry przepływu. Ta sama
wysokość nierówności na powierzchni przewodu może mieć istotne znaczenie w przypadku przewodów o
małych wymiarach przekroju poprzecznego, a z kolei może być zaniedbywalna przy wielkośrednicowych
rurociągach. Za miarodajną uznaje się zatem tzw. chropowatość względną, czyli odniesioną do liniowego
wymiaru charakteryzującego przekrój poprzeczny rurociągu. W przypadku rur kołowych chropowatość
względna

ε

najczęściej określana jest jako

d

k

=

ε

(9)

gdzie d jest średnicą rury.

Podsumowując więc powyższe rozważania można stwierdzić, że współczynnik oporów

liniowych

λ

jest funkcją dwóch wielkości – liczby Reynoldsa (charakteryzującej rodzaj ruchu) i

chropowatości względnej

λ

= f(Re,

ε

) (10)

7

a postać tej formuły zależy od wartości liczby Re, inna jest więc dla ruchu laminarnego, inna w strefie
przejściowej, jeszcze inna dla ruchu turbulentnego.

Badania oporów w zależności od Re i

ε

jako jeden z pierwszych prowadził Nikuradse.

Sztuczną chropowatość przewodu imitował on ziarnami piasku przyklejanymi na wewnętrznej
powierzchni rury. W rezultacie jego badań powstał wykres przedstawiający relację (10) w pełnym
zakresie liczb Reynoldsa, który to ze względu na charakterystyczny kształt określany jest często „harfą
Nikuradsego”. Dalsze badania, już dla naturalnej chropowatości przewodów, prowadzili m.in.
Colebrook i White, a później także Moody, Walden i inni. W rezultacie powstała kolejna wersja
wykresu, zwana wykresem Colebrooka i White’a lub wykresem Moody’ego (rys. 4). Z tego ostatniego
można – dla znanej wartości Re oraz danej chropowatości względnej odczytać wartość

λ.

Jeśli jednak

istnieje taka możliwość, lepszym sposobem określenia współczynnika oporów liniowych jest
wyznaczenie go na drodze eksperymentalnej.

10 2 10 10 10 10 10 10

3

3

4

5

6

7

8

.

λ

λ

0,080

0,072

0,064
0,056
0,048
0,040

0,036

0,032

0,028
0,024

0,04

0,03
0,02

0,01

0,006

0,002

0,001

0,0004

0,0001

0,00001

0,020

0,016

0,012

0,010

0,008

=

64 Re

strefa ruchu

laminarnego

strefa

przejściowa

strefa dobrze rozwniętego ruchu

turbulentnego (strefa "kwadratowego

prawa oporu")

k/d=

przewody
gładkie

Re

kr

Re

Rys. 4. Wykres zależności między współczynnikiem oporów liniowych

λ, liczbą Reynoldsa Re

i chropowatością względną

ε wg Colebrooka i White’a

Lokalne straty energii

Miejscowe opory przy przepływie związane są z lokalnie występującymi „przeszkodami”,

takimi jak zmiany średnic przewodu (gwałtowne lub łagodne – rys. 5a,b) zmiany kierunku
przepływu

(np. kolanka – rys. 5c, załamania przewodu), trójniki (a także czwórniki, rozdzielacze itp.),

armatura zamontowana na przewodzie

(regulacyjna – np. wszelkiego typu zawory, zasuwy, kurki,

pomiarowa– np. wodomierze itp.), wloty ze zbiornika do rurociągu i z rurociągu do zbiornika i inne.

Mimo znacznego zróżnicowania typu przeszkody, a co za tym idzie – lokalnego charakteru

przepływu (tzn. układu linii prądu w obrębie przeszkody, ewentualnego powstawania stref zawirowań,

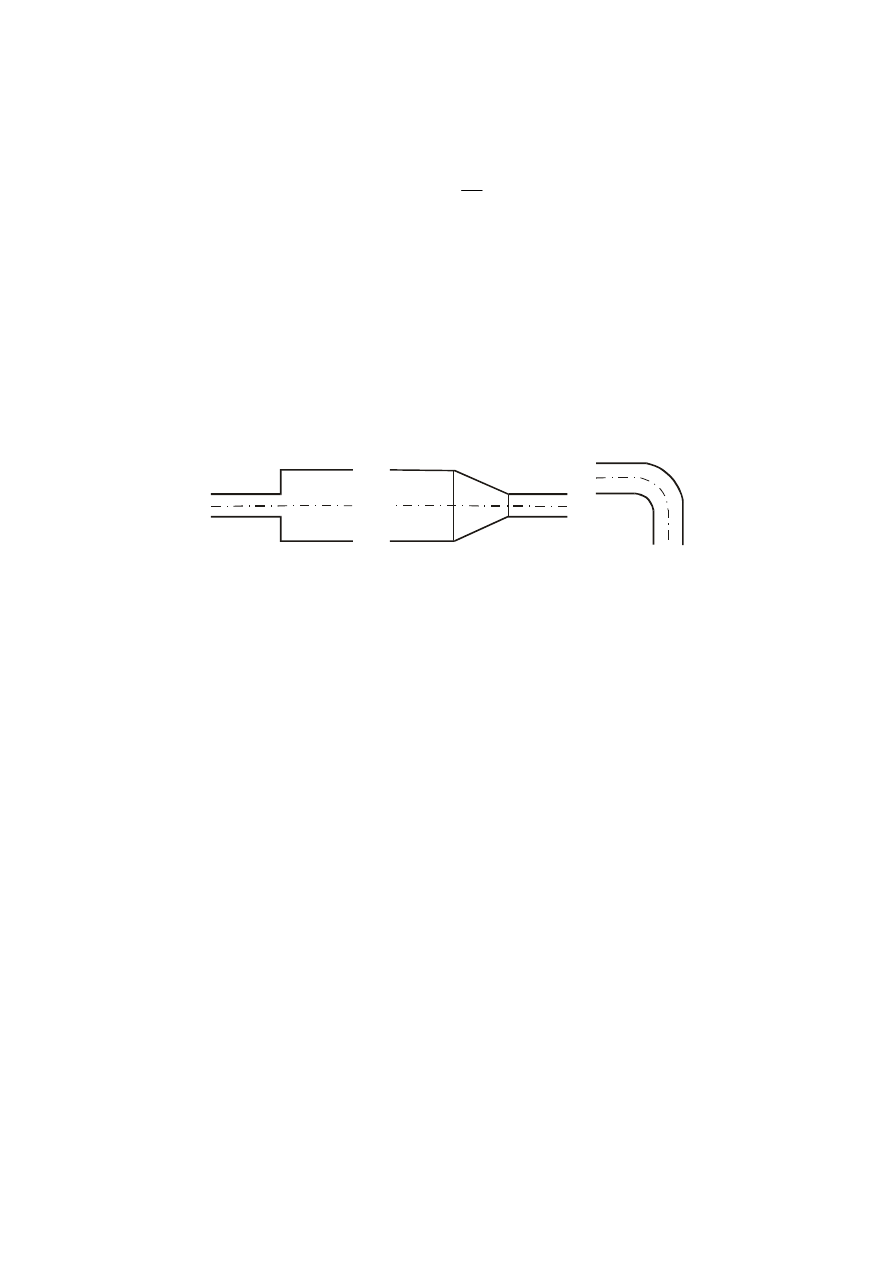
8

lokalnego wzrostu prędkości itp.), miejscowe straty energii obliczane są ze stosunkowo prostego
wzoru, jednakowego dla wszystkich typów przeszkody:

g

h

str

2

2

v

ζ

=

(11)

w którym

ζ

jest współczynnikiem oporów lokalnych, zależnym od typu przeszkody. Ze względu na

fakt, iż w przypadku niektórych kształtek następuje zmiana średniej prędkości przepływu (np. przy
rozszerzeniu przewodu), najczęściej przyjmuje się, że prędkość występująca w formule (11) oznacza
prędkość za przeszkodą, i dla takiego założenia wyznaczane są wartości współczynników oporu.
Możliwe jest również odnoszenie współczynnika strat lokalnych do prędkości przed przeszkodą. Przy
podawaniu wartości

ζ

informacja ta musi być jednak wyraźnie zaznaczona.

a)

b)

c)

Rys. 5. Przykłady kształtek powodujących lokalne straty energii mechanicznej:

a) gwałtowne rozszerzenie przewodu, b) łagodne zwężenie przewodu (konfuzor), c) kolanko 90

°

W

większości przypadków, w tym w przeważającej części zagadnień projektowych, wartości

współczynników oporów lokalnych określane są na podstawie tabel i ewentualnie danych producenta
kształtek. Zależą one od typu przeszkody i od jej cech specyficznych: np. w przypadku zmiany
powierzchni przekroju – od średnicy przewodu przed i za kształtką, dla zaworów – od rodzaju zaworu,
niekiedy od jego średnicy i stopnia otwarcia itp. Warto natomiast zwrócić uwagę, że współczynniki
przyjmowane na podstawie tabel (współczynniki teoretyczne) nie zależą od prędkości przepływu.
Oznacza to, że – zgodnie z (11) – wysokość strat energii na oporze lokalnym jest proporcjonalna do
kwadratu prędkości strumienia cieczy, co jest charakterystyczne dla ruchu turbulentnego. Z
praktycznego punktu widzenia jest to założenie słuszne, gdyż w typowych instalacjach i sieciach
mamy zawsze do czynienia z ruchem turbulentnym. Nie mniej jednak z formalnego punktu widzenia
należy wziąć pod uwagę także przypadki mniej typowe, w których wystąpi ruch laminarny lub
turbulentny w strefie przejściowej, a wówczas wartości współczynników podawane w tabelach mogą
znacznie odbiegać od rzeczywistych.

Przedstawiane w literaturze i podane wyżej sposoby określania współczynników oporów są w

większości przypadków wystarczające do typowych obliczeń inżynierskich. Jako załącznik do
instrukcji zamieszczono tabelę z typowymi wartościami współczynników oporów lokalnych (Zał.1.).
Podobnie jak w przypadku strat na długości, lepszą metodą prawidłowego wyznaczenia
współczynników oporów lokalnych jest metoda eksperymentalna dla konkretnej analizowanej
kształtki.

9

W ćwiczeniu zostanie przeprowadzone eksperymentalne wyznaczenie współczynników oporów
liniowych i lokalnych dla wybranego fragmentu rurociągu.

Określenie współczynnika oporu metodą doświadczalną

Wyznaczenie

współczynnika oporów lokalnych lub liniowych metodą laboratoryjną przebiega

w stosunkowo prosty sposób. Badaną kształtkę lub odcinek rury umieszcza się w przewodzie o znanej
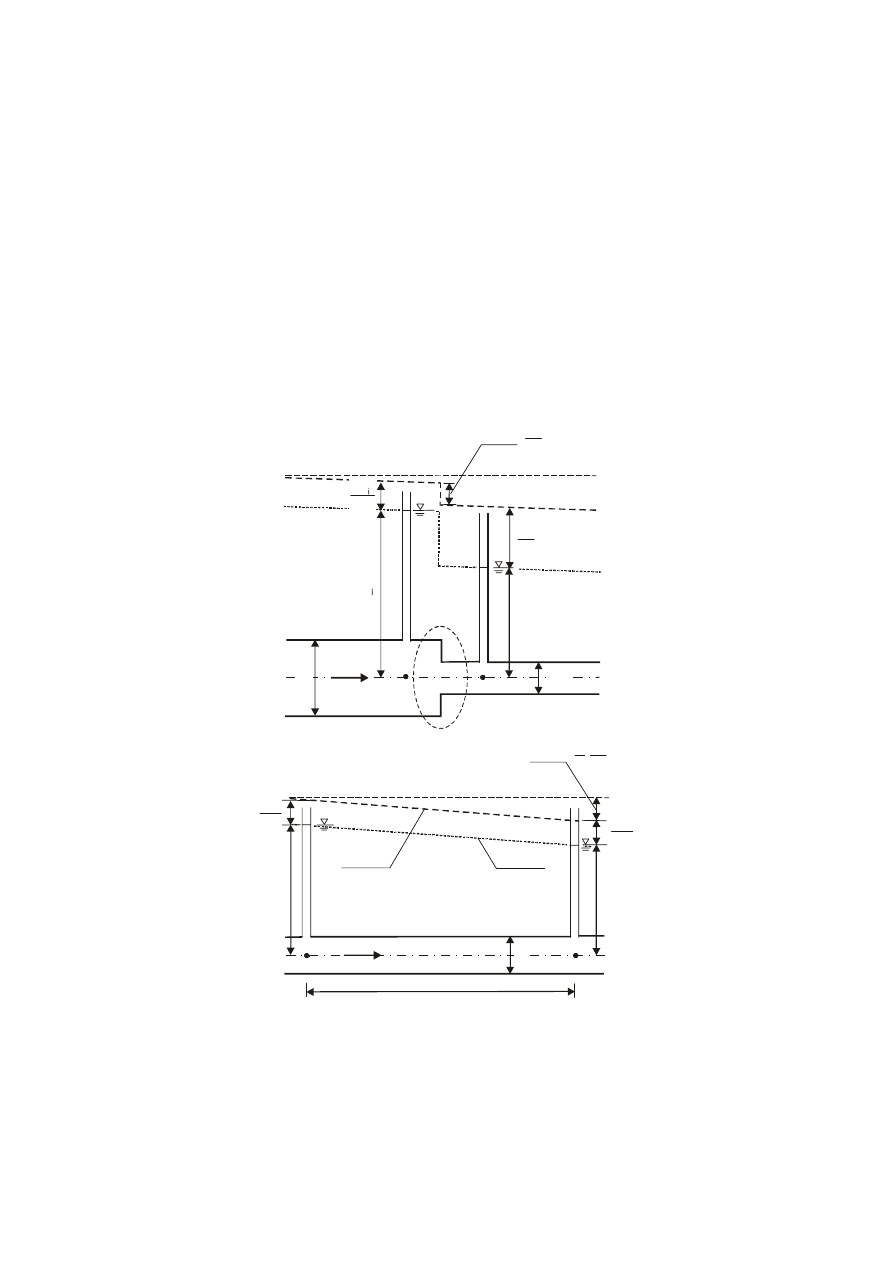
geometrii. W przekrojach i oraz i + 1 na końcach analizowanego wycinka rurociągu (czyli przed i za
kształtką lub na początku i końcu badanego odcinka rury – rys. 6a,b) montuje się piezometry (cienkie
przezroczyste rurki umożliwiające obserwację poziomu zwierciadła wody) lub inne urządzenia do
pomiaru ciśnienia.

i

i

i+1

i+1

h

h

Q

Q

d

i

d

i+1

i

2

v

2g

i+1

2

i+1

v

2g

2

2

i+1

i

v

v

2g

2g

h =

ζ

h =

λ

2

i+1

v

2g

2

v

2g

str

str

linia

ciśnienia

linia
ciśnienia

linia

energii

linia

energii

linia energii

dla cieczy nielepkiej

linia energii

dla cieczy nielepkiej

α

α

ζ

α

α

h

h

L

d

d

L

λ

a)

b)

Rys. 6. Schemat obliczeniowy do określania współczynnika oporów:

a) lokalnych, b) na długości

Po uruchomieniu zasilania następuje przepływ cieczy, którego natężenie Q należy pomierzyć, tak by
na tej podstawie określić prędkości przepływu w przewodzie (korzystając z zależności (5)). Dla

10

przekrojów i oraz i+1 określa się odpowiadające im wysokości energii mechanicznej, wyrażone
wartościami trójmianu Bernoulliego B

i

i B

i+1

zgodnie z (6). Różnica tych wartości pozwala ocenić

wysokość strat energii między przekrojami i oraz i + 1:

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

=

−

=

+

+

+

+

g

p

z

g

p

z

B

B

h

i

i

i

i

i

i

i

i

str

2

2

2

1

1

1

2

1

v

v

α

γ

α

γ

(12)

co dla z

i

= z

i+1

oraz przy zastosowaniu piezometrów jako urządzeń do pomiaru ciśnienia, prowadzi do

formuły:

(

)

g

h

g

h

g

h

h

i

i

i

i

i

i

str

2

2

2

2

1

2

2

1

1

2

+

+

+

−

+

∆

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

=

v

v

v

v

α

α

α

(13)

gdzie

∆h jest odczytaną różnicą poziomów zwierciadeł cieczy w piezometrach. Znając wysokość strat

na badanym odcinku, możemy z formuł (8) lub (11) wyznaczyć poszukiwaną wartość współczynnika
oporów.

Część III. (Sz).Modelowanie filtracji przez zaporę ziemną

Ruch wody w ośrodku porowatym zwany jest również przepływem filtracyjnym albo krócej

filtracją. Ośrodek porowaty składa się materiału tworzącego szkielet gruntowy oraz wolnych
przestrzeni (zwanych przestrzenią porową), tworzących skomplikowany system kanalików i połączeń,
którymi może płynąć woda. Ośrodki porowate możemy podzielić na naturalne i sztuczne. Naturalne
struktury wodonośne tworzące ośrodek porowaty wynikają ze skomplikowanej budowy geologicznej,
która kształtuje stosunki hydrogeologiczne. Do systemów sztucznych należą między innymi filtry,
złoża jonitów, węgla aktywnego.

Jednym z podstawowych parametrów charakteryzujących filtracyjne własności ośrodka jest

porowatość

. Współczynnik porowatości objętościowej (współczynnik porowatości) definiowany

jest jako graniczna wartość stosunku objętości porów

∆V

p

w ośrodku porowatym do objętości całej

próbki ośrodka

∆V:

V

V

n

p

g

V

V

∆

∆

=

∆

→

∆

lim

(14)

gdzie

∆V

g

jest tzw. objętością graniczną. Wynika ona z konieczności dobrania odpowiednio

dużej objętości próbki

∆V, tak aby uniknąć efektów mikroskalowych (zbyt mała objętość

może w całości obejmować ziarna szkieletu gruntowego albo przestrzeń porową i w takim
przypadku współczynnik porowatości przyjmowałby wartość 0 albo 1). Objętość graniczna
∆V

g

określa więc minimalną objętość próbki przy której współczynnik porowatości nie

zmienia się znacząco w funkcji wielkości próbki. Nie wszystkie jednak przestrzenie porowe
umożliwiają przepływ wody. Mogą one być na przykład odizolowane od globalnej struktury
kanalików. Z kolei w innej części przestrzeni porowej, zdolnej do prowadzenia wody ze
względu na ich drożność, przepływ mogą uniemożliwiać siły adhezji. Dlatego też w filtracji

11

bierze udział tylko część przestrzeni porowej zwana objętością efektywną

∆V

e

.

Współczynnik porowatości efektywnej n

e

definiowany jest następująco:

V

V

n

e

g

V

V

e

∆

∆

=

∆

→

∆

lim

(15)

Prędkość filtracji

Jak już wspomniano, decydującą rolę w ruchu cieczy odgrywa układ kanalików przestrzeni

porowej. Linie prądu przepływu rzeczywistego mają bardzo skomplikowany kształt. Jednakże podczas
przepływu woda przemieszcza się w określonym kierunku zgodnie z działającymi czynnikami
wymuszającymi przepływ (spadek ciśnienia, siła ciężkości). Z uwagi na fakt, iż prędkość przepływu w
poszczególnych kanalikach jest praktycznie niemożliwa do określenia, do obliczeń przyjmuje się
uproszczenie polegające na przyjęciu „uśrednionej” prędkości przepływu zwanej prędkością filtracji.
Prędkość filtracji jest to zatem pewna fikcyjna prędkość, z jaką płynęłaby dana ilość wody, gdyby
przepływ odbywał się w całej objętości, a nie tylko w przestrzeni porów (czyli tak, jakby z gruntu
usunięto wszystkie ziarna, nie zmieniając wydatku). Z definicji prędkość filtracji (prędkość
Darcy’ego) jest wynikiem całkowania pola prędkości w objętości

∆V i podzieleniu całki przez ∆V.

( )

∫

∆

∆

∆

=

V

f

V

d

V

v

v

1

(16)

Wielkość v

f

określana jest również jako wydatek jednostkowy (strumień jednostkowy,,

strumień Darcy’ego), ponieważ określa wydatek cieczy z uwzględnieniem kierunku jej ruchu przez
jednostkowe pole powierzchni prostopadłe do tego kierunku.

W rzeczywistości jednak ciecz przepływa tylko przez przestrzenie między ziarnami szkieletu

gruntowego, a zatem rzeczywista uśredniona prędkość przepływu przez grunt, tzw. prędkość porowa
określona jest relacją:

( )

∫

∆

∆

∆

=

V

p

p

V

d

V

v

v

1

(17)

Prędkość filtracji i prędkość porową łączy następująca zależność:

e

f

p

n

v

v

=

(18)

Prawo Darcy’ego

Przy rozwiązywaniu problemów dotyczących filtracji zasadniczą rolę odgrywa podstawowe

prawo filtracji, sformułowane przez Henry’ego Darcy w 1856 roku w efekcie badań piaskowych
filtrów wodociągowych miasta Dijon (Francja). Darcy stwierdził, iż strumień jednostkowy wody
przepływający przez grunt (prędkość filtracji) jest wprost proporcjonalny do spadku hydraulicznego

I,

czyli różnicy wysokości piezometrycznych

∆

ϕ

na dystansie

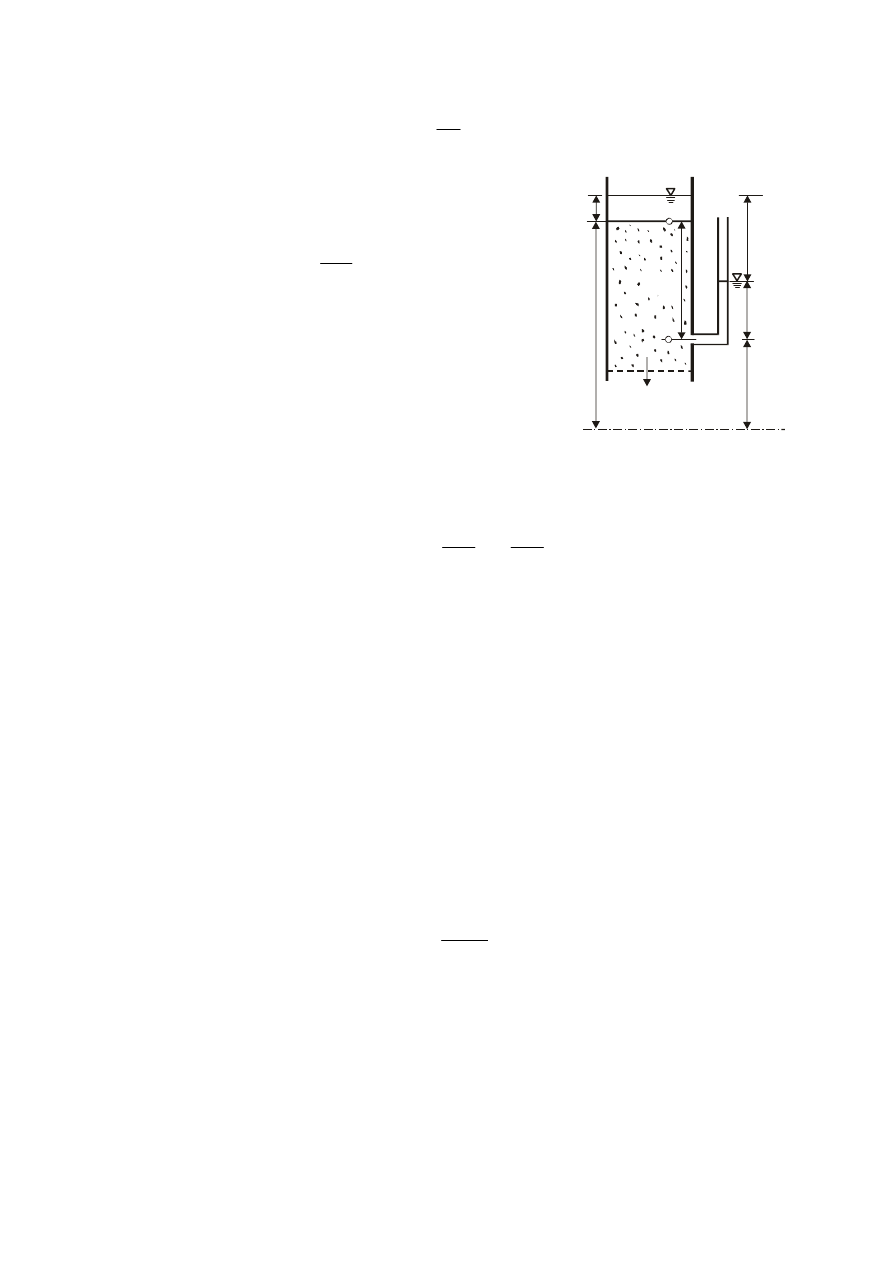
∆L na którym ta różnica występuje (rys.

7):

12

I

K

L

K

f

⋅

=

∆

∆

=

ϕ

v

(19)

gdzie

ϕ

oznacza wysokość linii ciśnień (wysokość piezometryczną)

równą sumie wysokości położenia

z i ciśnienia h (wysokości

zwierciadła wody w piezometrze):

h

z

g

p

z

+

=

⋅

+

=

ρ

ϕ

(20)

Jest to trójmian Bernoulliego uproszczony przez odrzucenie członu
v

2

/2g, ze względu na małą wartość prędkości v.

Wielkość K jest współczynnikiem proporcjonalności

zwanym współczynnikiem przewodności hydraulicznej lub też
współczynnikiem filtracji

. Jednostka współczynnika filtracji

odpowiada jednostce prędkości. Jego wartość uzależniona jest od
własności ośrodka porowatego (

n – współczynnik porowatości, d

m

–

średnica miarodajna) oraz od własności fizycznych przesączającej
się cieczy (

ρ

– gęstość,

µ

– dynamiczny współczynnik lepkości)

µ

ρ

µ

ρ

g

k

g

d

n

c

K

m

⋅

⋅

=

⋅

⋅

⋅

⋅

=

2

(21)

gdzie

k [m

2

] jest współczynnikiem przepuszczalności (współczynnik Darcy’ego) uzależnionym tylko

od własności ośrodka porowatego.
Powyższa relacja nie pozwala na określenie liczbowej wartości współczynnika Darcy’ego i
tym samym współczynnika filtracji, ponieważ została przedstawiona z dokładnością do stałej

c.

Dlatego też współczynnik filtracji wyznacza się w rzeczywistości doświadczalnie (laboratoryjnie albo
w warunkach polowych) lub też przy użyciu uproszczonych wzorów teoretycznych.

Prawo Darcy’ego podlega pewnym ograniczeniom. Aby możliwy był przepływ wody,

niezbędne jest przekroczenie minimalnej wartości gradientu wysokości piezometrycznej. To „dolne
ograniczenie” prawa Darcy’ego związane jest z działaniem sił adhezji. W praktyce inżynierskiej
utrudnienie stanowi „górne ograniczenie” prawa Darcy’ego, co związane jest z pojawieniem się ruchu
turbulentnego przy większych prędkościach przepływu. Informacji o tym, czy rozważany przepływ ma
charakter laminarny czy turbulentny, dostarcza liczba Reynoldsa, która dla przepływu przez ośrodek
porowaty definiowana jest najczęściej jako

ν

e

f

d

⋅

=

v

Re

(22)

W powyższym wzorze

d

e

oznacza średnicę efektywną ziaren, która określa średnicę ziaren kulistych

fikcyjnego gruntu idealnie jednorodnego, który wykazuje taką samą przepuszczalność i stawia taki
sam opór przepływającej wodzie jak grunt rzeczywisty. Średnica efektywna zwykle wynosi

d

10

,

co

oznacza średnicę ziaren, które wraz z mniejszymi stanowią 10% ciężaru badanej próbki gruntu.

Krytyczna liczba Reynoldsa w przypadku ruchu filtracyjnego wynosi w przybliżeniu 5

Wartości powyższe stanowią górne ograniczenie stosowalności liniowego prawa Darcy’ego. Ze
względu na wspomniane wcześniej „ograniczenie dolne” związane z działaniem sił adhezji,

1

2

poziom porównawczy

v

z

h

f

1-2

1

1

∆ϕ

1-2

∆L

h

2

2

z

Rys. 7. Idea doświadczenia

Darcy’ego

13

ostatecznie można uznać, że zakres stosowalności prawa Darcy’ego ogranicza się do przedziału liczb
Reynoldsa

〈1,5〉.

Filtracja przez zaporę ziemną

Rozwiązania zagadnień filtracyjnych w większości przypadków ograniczają się do problemów

ustalonych w czasie. Cząsteczki wody poruszające się w ośrodku gruntowym przebywają bardzo
skomplikowaną drogę. Dlatego też w ogólnym przypadku prędkości cząsteczek wody są różne w
różnych punktach badanego obszaru przepływu. Taki rodzaj ruchu jest określamy mianem ruchu
niejednostajnego

*

. Aby możliwe było opisanie ruchu krążącej wody w ośrodku porowatym

równaniami fizyki matematycznej wprowadzono pojęcie prędkości filtracji v

f

, która (będąc wielkością

fikcyjną) w pewnym uproszczeniu pozwala rozwiązać zagadnienia praktyczne. W trójwymiarowym,
ustalonym przypadku ruchu wód gruntowych w każdym punkcie obszaru filtracji zmieniają się
prędkość i potencjał filtracyjny

ϕ

uzależniony od ciśnienia

p. W celu rozwiązania należy zatem

znaleźć 4 niewiadome:

)

,

,

(

z

y

x

v

x

f

,

)

,

,

(

z

y

x

v

y

f

,

)

,

,

(

z

y

x

v

z

f

oraz

)

,

,

(

z

y

x

p

lub

)

,

,

(

z

y

x

ϕ

.

Przesączanie wody przez zaporę ziemną jest w istocie rzeczy zagadnieniem dwuwymiarowym

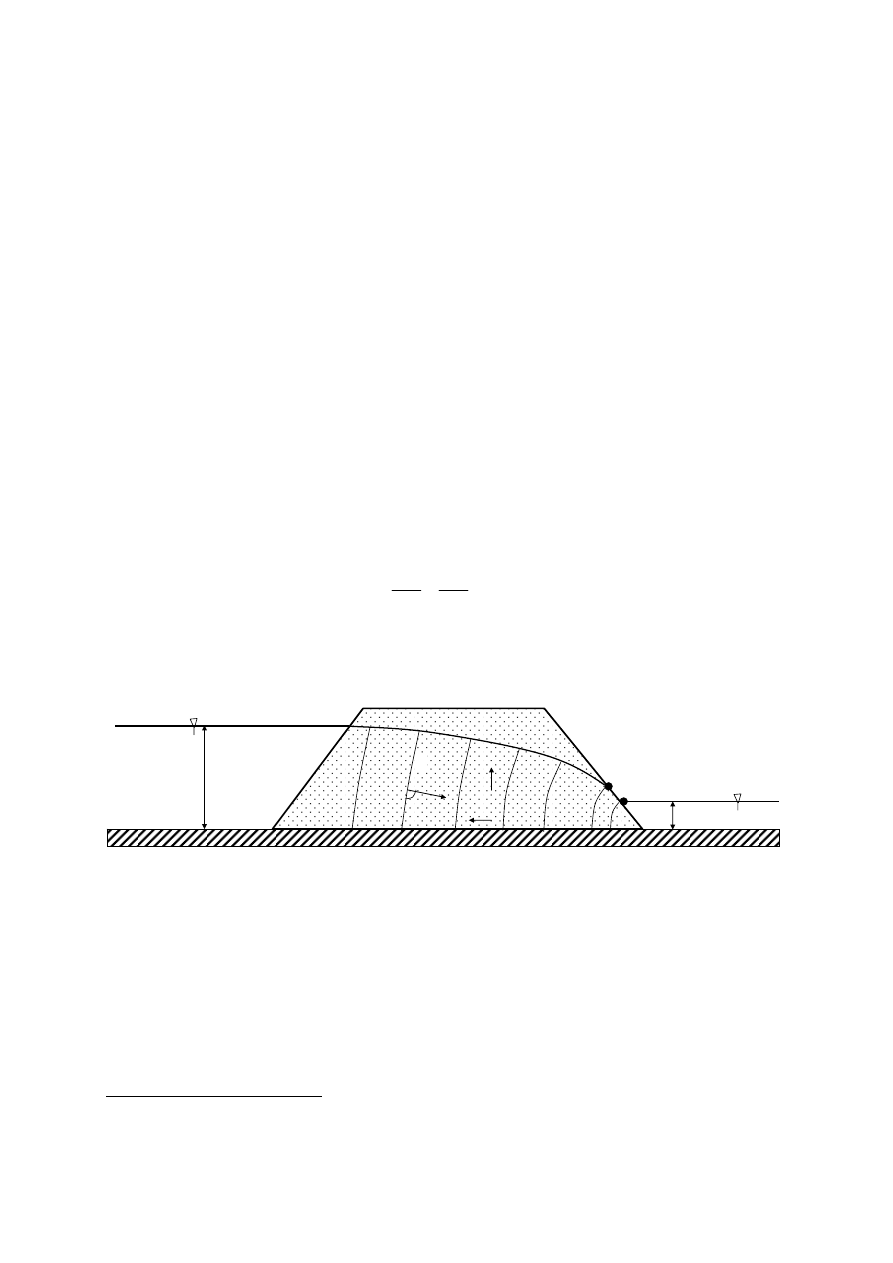
(rys. 8). Woda przepływa wzdłuż linii prądu ograniczonych dolną nieprzepuszczalną powierzchnią
oraz linią swobodnego zwierciadła wody, zwaną krzywą depresji. Jak widać na rys. 8, linie prądu nie
są wzajemnie równoległe do siebie. W równaniu opisującym przesączanie wody przez zaporę ziemną,
zwanym równaniem Laplace’a (8) nie występuje współczynnik filtracji:

0

2

2

2

2

=

∂

∂

+

∂

∂

z

x

ϕ

ϕ

(23)

Stwierdzić zatem można iż kształt krzywej depresji nie jest tu uzależniony od warunków

filtracyjnych gruntu.

i

ϕ

W

1

W

2

H

h

0

x

z

v

Rys. 8. Rzeczywisty schemat przesączania wody przez groblę ziemną

lub oleju przez szczelinę urządzenia szczelinowego

Równaniem formalnie identycznym z (23) opisuje powolny przepływ cieczy (korzystnie, jeśli ma ona
dużą lepkość) pomiędzy dwiema sztywnymi powierzchniami. Jeżeli zatem przepływ wody w gruncie
zastąpimy (w ramach laboratoryjnego modelowania zjawiska) przepływem oleju w pionowej
szczelinie między dwiema płaskimi płytami, to otrzymamy analogiczny kształt krzywej depresji,
wynikający z formalnie identycznych równań i warunków brzegowych. Należy podkreślić, iż istnieje

*

Ruch, w którym współrzędne wektora prędkości nie zmieniają się w przestrzeni nazywamy ruchem

jednostajnym. Przykładem jednostajnego ruchu wody w gruncie jest przepływ wody w kolumnie filtracyjnej, na
podstawie którego doświadczalnie określa się współczynnik filtracji gruntu (F)

14

pewna maksymalna szerokość szczeliny, przy której zjawiska przepływu w szczelinie będą
wykazywać analogię do filtracji wody w gruncie. Szerokość szczeliny wynika z kryterium Reynoldsa
wyrażonego równymi wartościami liczby Reynoldsa modelu i przepływu rzeczywistego.
Omówiony

wyżej typ zadania dwuwymiarowego, opisanego równaniem (23), jest dość

złożony. W celu jego uproszczenia często możemy wykorzystać pewną regularność przepływu. Jeżeli
mianowicie krzywizny linii prądu nie są znaczne, to możemy pominąć zmienność prędkości w
poprzek strumienia i posłużyć się prędkością średnią v

f

. Innymi słowy – możemy wtedy potraktować

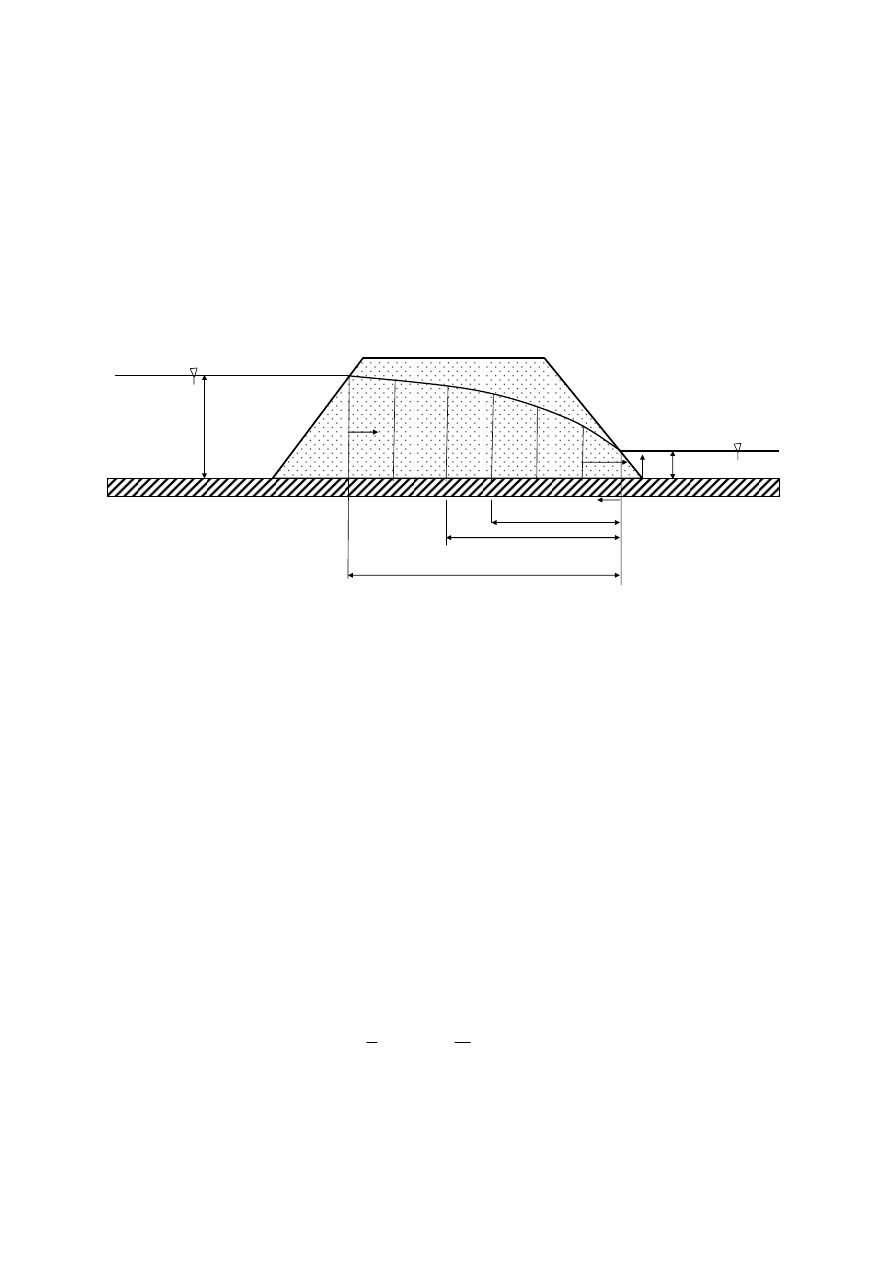
ruch płaski (dwuwymiarowy) jako ruch jednowymiarowy. Jest to istota założenia Dupuita, który
zaproponował jego stosowanie w roku 1857 (rys. 9).

L

H

h

0

s

h

s

1

s

h

h

1

v

f

v

f

Rys. 9. Schemat przesączania wody przez groblę ziemną wynikający z uproszczenia Dupuita

Dodatkowym

elementem

wynikającym z tego założenia jest pominięcie w obliczeniach tzw.

obszaru wysączania

zwanego inaczej zeskokiem hydraulicznym (rys. 8). Porównując krzywą

depresji z obliczoną przy uwzględnieniu założenia Dupuita z krzywą rzeczywistą, widać że krzywa
depresji łączy się bezpośrednio z punktem W

2

podczas gdy krzywa rzeczywista zwilża krawędź grobli

na odcinku pomiędzy punktami W

1

, W

2

.

Jest to efekt zdecydowanej niejednostajności ruchu w tym

rejonie, ponieważ w rzeczywistości ciśnienie piezometryczne poniżej punktu W

1

musi być większe,

niż poniżej punktu W

2

. Wynika to z prostopadłości linii prądu do „zakrzywionych” linii potencjału

piezometrycznego. Tak więc strefa wysięku wód gruntowych ograniczona punktami W

1

, W

2

przy

uproszczonych obliczeniach nie występuje. W rzeczywistych warunkach w strefie wysięku może
dochodzić do powolnego wynoszenia materiału gruntowego. Proces ten zwiększa się wraz ze
zwiększaniem potencjału filtracyjnego wynikającego z podnoszenia się wód powierzchniowych.
Podobnie wynoszenie materiału gruntowego następuje pod drogami w rejonach gdzie występuje
znaczna różnica poziomów zwierciadła wód gruntowych po przeciwległych stronach drogi.

Po uwzględnienia założenia Dupuita można uzyskać analityczne wyznaczenie wydatku oraz

kształtu krzywej depresji. W wyniku rozdzielenia zmiennych i całkowania otrzymamy postać:

(

)

(

)

s

s

K

q

h

h

−

=

−

1

2

1

2

2

1

, (24)

w której

s oznacza współrzędną liczoną wzdłuż kierunku przepływu. Po uwzględnieniu warunków

brzegowych:

15

H

h

L

s

h

h

s

=

⇒

=

=

⇒

=

0

0

wydatek jednostkowy (na 1mb grobli) określony jest następującą zależnością.:

(

)

2

0

2

2

h

H

L

K

q

−

=

, (25)

w której K jest współczynnikiem filtracji.
Rzędną h krzywej depresji wyznaczyć można z zależności (24) po uwzględnieniu warunku
brzegowego

H

h

L

s

=

⇒

=

:

(

)

L

s

h

H

h

h

⋅

−

+

=

2

0

2

2

0

(26)

Formuła (26) potwierdza, iż kształt krzywej depresji nie zależy od współczynnika filtracji. Dla danych
h

0

, H, oraz L kształt ten jest taki sam bez względu na rodzaj gruntu.

3. Schematy stanowisk pomiarowych i przebieg pomiarów

Część I. Wyznaczenie krytycznej liczby Reynoldsa

Schemat stanowiska pomiarowego

Ćwiczenie wykonywane jest na stanowisku o konstrukcji przedstawionej na rys. ????,

zbliżonej do konstrukcji stanowiska badawczego Reynoldsa.

Stanowisko pomiarowe składa się z następujących elementów:

•

zbiornika zasilającego

, zaopatrzonego w zawór doprowadzający wodę do zbiornika, krawędź

przelewową, która umożliwia utrzymanie ustalonych warunków przepływu oraz zawór spustowy;

•

dwóch przewodów o przekroju kołowym

, wykonanych ze szkła organicznego, umożliwiającego

prowadzenie obserwacji, wyprowadzonych ze zbiornika zasilającego i zakończonych zaworami
umożliwiającymi regulację natężenia przepływu;

•

zbiorniczków z barwnikiem,

wraz z przewodami doprowadzającymi barwnik do przewodów,

wyposażonych w zawory umożliwiające regulację natężenia dopływu barwnika;

oraz urządzeń pomocniczych:

•

naczynia do pobierania wody wypływającej z przewodów w celu pomiaru natężenia przepływu;

•

cylindra miarowego do precyzyjnego określania ilości pobranej wody;

•

stopera;

•

termometru do określenia temperatury przepływającej cieczy;

•

urządzeń odpływowych.

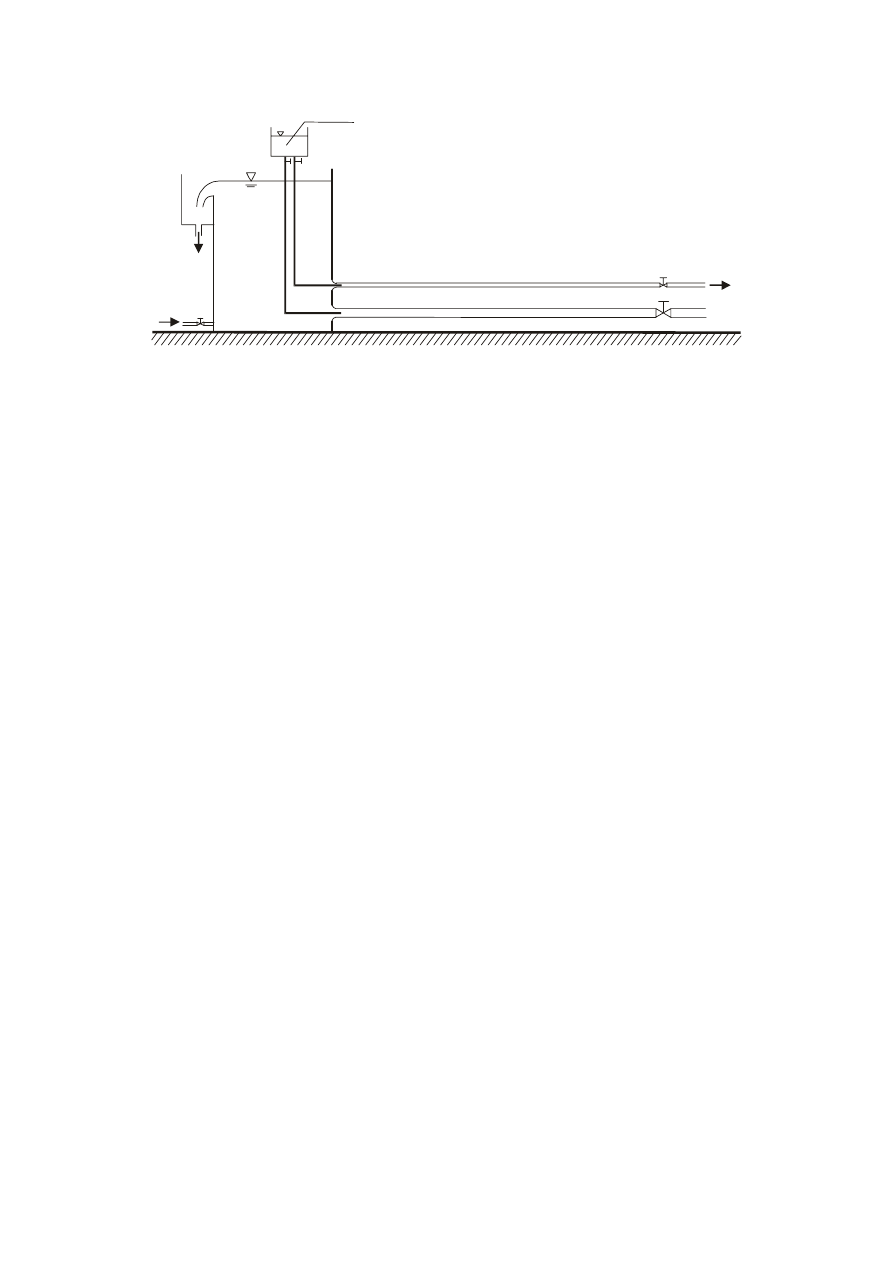
16

d=10 mm

d=14 mm

Q

barwnik

Z1

Z2

Z3

Rys. 10. Schemat stanowiska do wyznaczenia dolnej krytycznej liczby Reynoldsa

Przebieg doświadczenia

W

ćwiczeniu dla jednego z dwóch przewodów należy wywołać przejście z ruchu laminarnego

w turbulentny, a w dalszej kolejności przejście odwrotne - z ruchu turbulentnego w laminarny i w
każdym przypadku określić wartość krytycznej liczby Reynoldsa.

Czynności przygotowawcze

W pierwszym etapie wykonywania ćwiczenia należy:

1) otworzyć zawór doprowadzający wodę do zbiornika zasilającego Z1 tak, aby uruchomić

przelew. Uwaga: woda powinna przelewać się przez krawędź przelewową w zbiorniku
zasilającym w ciągu całego czasu wykonywania ćwiczenia. Należy zatem odpowiednio często
kontrolować krawędź przelewową, a w razie potrzeby zwiększyć ilość cieczy dopływającej do
zbiornika zaworem Z1. W przeciwnym razie może nastąpić opróżnianie zbiornika, a warunki
przepływu nie będą ustalone;

Obserwacja przejścia z ruchu laminarnego w turbulentny

W tym celu należy:

2) wywołać przepływ w jednym z przewodów, poprzez delikatne otwarcie zaworu regulacyjnego

na jego końcu (Z2). Ustawić małe natężenie przepływu w przewodzie;

3) doprowadzić barwnik do przewodu przez otwarcie zaworu znajdującego się w przewodzie

doprowadzającym (Z3); zaobserwować cienką strugę barwnika w przewodzie, świadczącą o
przepływie laminarnym. W razie potrzeby skorygować ilość barwnika doprowadzanego do
przewodu;

4) delikatnie zwiększając stopniowo prędkość przepływu w przewodzie (poprzez regulację

przepływu zaworem na końcu przewodu Z2), zaobserwować możliwie dokładnie moment
przejścia ruchu laminarnego w turbulentny

. W momencie zaobserwowania zmiany charakteru

ruchu należy przerwać manipulowanie przy zaworze regulacyjnym;

5) zakręcić dopływ barwnika;
6) dwukrotnie metodą objętościową dokonać pomiaru natężenia przepływu (poprzez pomiar

czasu przepływu określonej ilości wody, pobieranej za pomocą podstawionego naczynia;

17

każdorazowo przelać zawartość naczynia do cylindra miarowego i dopiero wówczas odczytać
objętość);

7) dokonać pomiaru temperatury cieczy w zbiorniku zasilającym;

Obserwacja przejścia z ruchu turbulentnego w laminarny

W tym celu należy:

8) ustawić duże natężenie przepływu w przewodzie;
9) doprowadzić barwnik do przewodu;

10) zmniejszając prędkość przepływu w przewodzie zaobserwować możliwie dokładnie moment

przejścia ruchu turbulentnego w laminarny

;

11) zakręcić dopływ barwnika;
12) dwukrotnie metodą objętościową dokonać pomiaru natężenia przepływu;
13) dokonać pomiaru temperatury cieczy w zbiorniku zasilającym;
14) zakręcić zawór na końcu przewodu.

Uwaga

: obserwacji charakteru ruchu cieczy w przewodzie należy dokonywać w obszarze w pełni

ukształtowanego profilu prędkości, tj. w odległości L

w

≥ 30 d od wlotu przewodu, gdyż zaburzenia

powstające w strefie wlotu ze zbiornika do przewodu mogą prowadzić do mylnej oceny charakteru
przepływu.

Opracowanie wyników pomiarów

W opracowaniu wyników eksperymentu należy:

1) na podstawie pomierzonej temperatury określić współczynnik lepkości cieczy (przy wykorzystaniu

wzorów (2) i (3));

2) na podstawie pomierzonych dwukrotnie czasów

t i objętości przepływającej cieczy V określić

dwukrotnie natężenie przepływu, zgodnie z zależnością:

t

V

Q

=

Wynik uśrednić;
3) na podstawie wyznaczonego natężenia przepływu i znanej średnicy przewodu określić prędkość

przepływu cieczy w przewodzie (zgodnie z relacją (5));

4) określić wartość krytycznej liczby Reynoldsa dla każdej zmiany rodzaju ruchu (korzystając ze

wzoru (4)).

Wyniki zebrać tabeli (tab. 1).

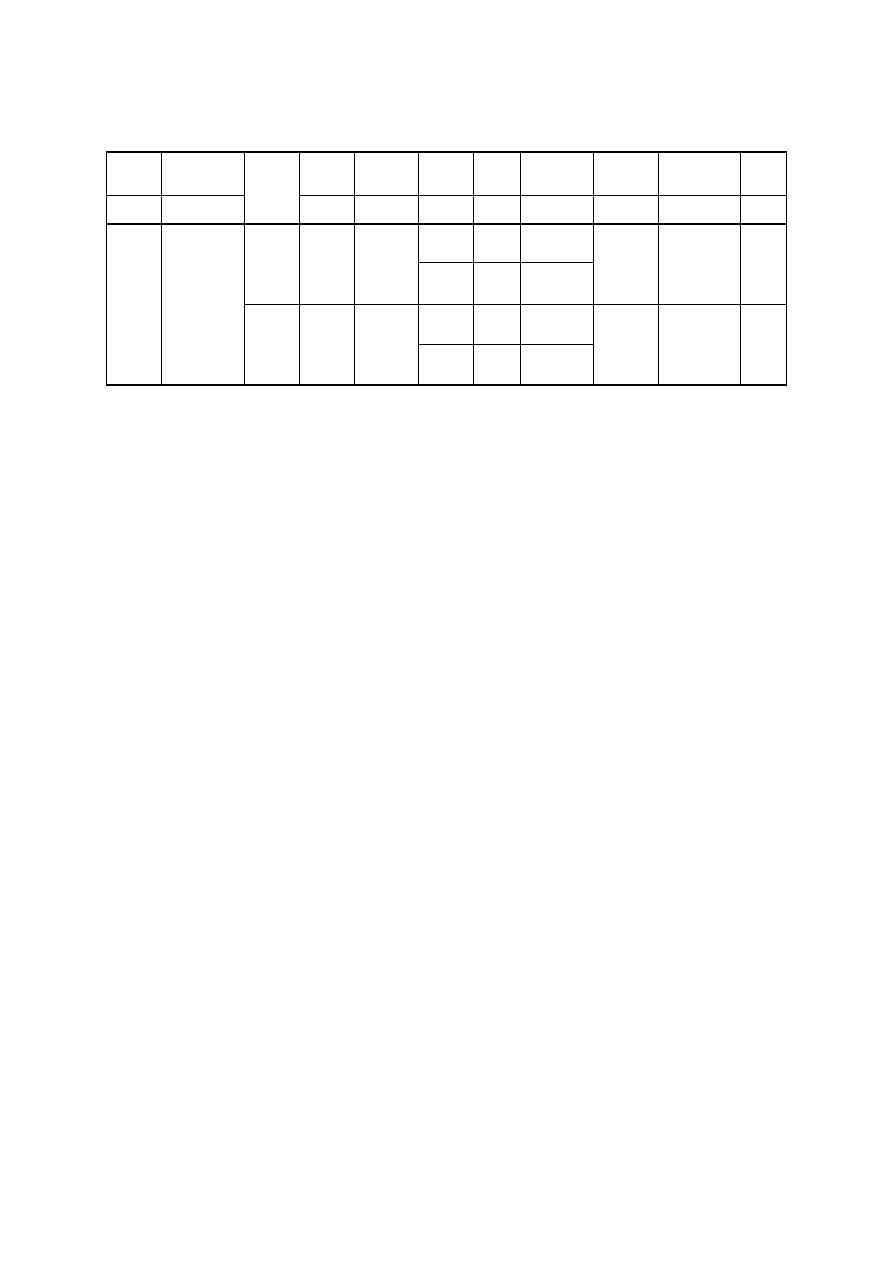
18

Tabela 1

Tabela pomiarowo-obliczeniowa do wyznaczenia krytycznej liczby Reynoldsa

d

F=

πd

2

/4

T

ν

V t Q=V/t Q

śr

v=Q

śr

/F Re

[cm] [cm

2

]

Obserwo

wan

e

zja

w

is

ko

[

°C]

[cm

2

/s] [cm

3

] [s] [cm

3

/s] [cm

3

/s] [cm/s] [

−]

laminarny

→

turbulentny

turbulentny

→

laminarny

Część II. (R). Opory ruchu w rurociągach

Schemat stanowiska pomiarowego
Pomiary II części ćwiczenia prowadzone są dla wybranego (określonego przez prowadzącego
ćwiczenia) odcinka rurociągu przedstawionego na rys. 11. W skład stanowiska pomiarowego
wchodzą:

•

zbiornik górny

wraz z przewodami zasilającymi rurociąg i przelewem umożliwiającym

utrzymanie stałego poziomu wody w zbiorniku,

•

rurociąg pomiarowy

, złożony z odcinków przewodów wykonanych z różnych materiałów (stal

ocynkowana, miedź, polipropylen), połączonych szeregiem różnorodnych kształtek (kolanek,
zmian średnic rury, złączek), umieszczony na poziomym stole pomiarowym,

•

zestaw 36 piezometrów, ponumerowanych od 0 do 35, podłączonych w charakterystycznych
punktach przewodu i umieszczonych na zbiorczej tablicy ułatwiającej odczyt (piezometr nr 0
wskazuje położenie zwierciadła wody w zbiorniku górnym i służy jako piezometr porównawczy),

•

wodomierz

, umożliwiający pomiar objętości przepływającej cieczy,

•

zawór regulacyjny

, pozwalający na regulację natężenia przepływu przez rurociąg,

•

zbiornik dolny

, do którego odprowadzana jest woda wypływająca z rurociągu,

•

pompa

, wraz z przewodem ssawnym i tłocznym, łączącymi zbiornik dolny i zbiornik górny,

umożliwiająca pracę systemu w układzie zamkniętym.

Przebieg doświadczenia

W tej części doświadczenia należy:
1) otworzyć zawór regulacyjny na końcu rurociągu i ustalić żądany przepływ (w konsultacji z

prowadzącym ćwiczenie);

2) dwukrotnie określić natężenie przepływu, mierząc za pomocą stopera czas przepływu ustalonej

objętości cieczy przez wodomierz. Wyniki zanotować w tab. 2. Objętość należy tak dobrać, by czas

19

zasilanie

1

2

3

4

9

10

11

18

19

20

17

16

24

25

26

27

28

35

34

odpływ

5

6

7

8

12

13

14

15

21

22

23

31

30

29

32

33

OC

OC

OC

OC

Cu

Cu

Cu

Cu

Cu

PP

PP

PP

PP

PP

-0.44-

-1.37-

-2.89-

-2.73-

-1.32-

-0.59-

-0.39-

-0.62-

-2.81-

-2.76-

-1.40-

-2.48-

-0.59-

-0.63-

1
2

3
4

1
2

1
2

1
2

1
2

3
4

1
2

3
4

22

22/15

20/25

25/50

50/25

32/25

20/15

35/22

22/35

20/32

1

1

26

1
2

3

4

50/25

Oznaczenia:

PP - rura z polipropylenu

Cu - rura miedziana

OC - rura stalowa ocynkowana

- 1.40 - - długość przewodu w metrach

zawór

wodomierz

zmiana średnicy rury

kolanko

śrubunek

piezometr

- zmiana średnicy rury

(wymiary w calach)

- zmiana średnicy rury

(wymiary w milimetrach)

Zestawienie średnic nominalnych i wewnętrznych rur

rury ocynkowane

1

2

1
2

3
4

“

“

“

1

φ

φ

φ

φ

φ

φ

15 mm

21 mm

41 mm

średnica

nominalna

średnica
wewnętrzna

rury miedziane

20 mm

13 mm

32 mm

φ

φ

φ

φ

φ

φ

średnica

nominalna

średnica

wewnętrzna

15

22

35

rury z polipropylenu

21 mm

13 mm

16.5 mm

43 mm

φ

φ

φ

φ

φ

φ

φ

φ

średnica

nominalna

średnica
wewnętrzna

25

32

20

50

Rys.11. Schemat rurociągu w ćwiczeniu R

20

pomiaru nie był krótszy niż 5 minut; (

Uwaga: Tabela 2 oraz przedstawiona w dalszej części instrukcji

tabela 3 są przygotowane dla kompletnych pomiarów dla wszystkich 35 piezometrów. W ćwiczeniu
należy wypełnić tylko te fragmenty tabel, które odpowiadają wybranemu odcinkowi rurociągu).

3) określić położenia zwierciadeł wody w kolejnych piezometrach na wybranym odcinku (wskazanym

przez prowadzącego ćwiczenia). Poziomy te określa się korzystając z umieszczonej na tablicy
podziałki, pamiętając, że zgodnie z tą podziałką wartość odczytu wzrasta w miarę przesuwania się
w dół, a zatem wskazuje ona obniżenie zwierciadła wody w stosunku do poziomu zerowego,
umieszczonego na górze tablicy. Wyniki zanotować w tab. 2;

4) pomierzyć temperaturę wody w zbiorniku dolnym w celu określenia liczb Reynoldsa i charakteru

przepływu.
Pomiary z punktów 2) do 4) powtórzyć dla innego natężenia przepływu wody przez rurociąg.
Przepływy każdorazowo zmienia się za pomocą zaworu regulacyjnego na końcu rurociągu.

Opracowanie wyników pomiarów

Dla każdego z dwóch natężeń przepływu należy:
1) na podstawie pomiaru czasu i objętości określić wydatek, wartości uzyskane z dwukrotnych

pomiarów uśrednić (tab. 2);

2) dla każdego z przepływów na podstawie odczytów z piezometrów określić różnice poziomów

zwierciadeł cieczy

∆h w kolejnych piezometrach na wybranych odcinkach (tab. 3); (uwaga: dla

każdego przepływu należy przygotować oddzielną tab.3)

3) obliczyć prędkości przepływu na analizowanych przekrojach rurociągu, korzystając z równania

ciągłości (5);

4) obliczyć wysokości strat energii mechanicznej w wybranych przekrojach na analizowanych

odcinkach rurociągu, korzystając z formuły (13). Do obliczeń przyjąć wartość

α

=1.

5) określić wartości współczynników oporów, odpowiadających kolejnym odcinkom rurociągu (z

formuł (8) lub (11), zależnie od typu oporu);

6) określić liczbę Reynoldsa dla analizowanych odcinków rurociągu (tab. 3) i określić charakter

panującego tam ruchu;

7) dla wybranych odcinków rurociągu oszacować teoretyczne wartości współczynników oporu. W

przypadku współczynnika

λ

skorzystać z wykresu Colebrooka-White’a, natomiast w przypadku

oporów lokalnych – z zał.1.

21

Tabela 2

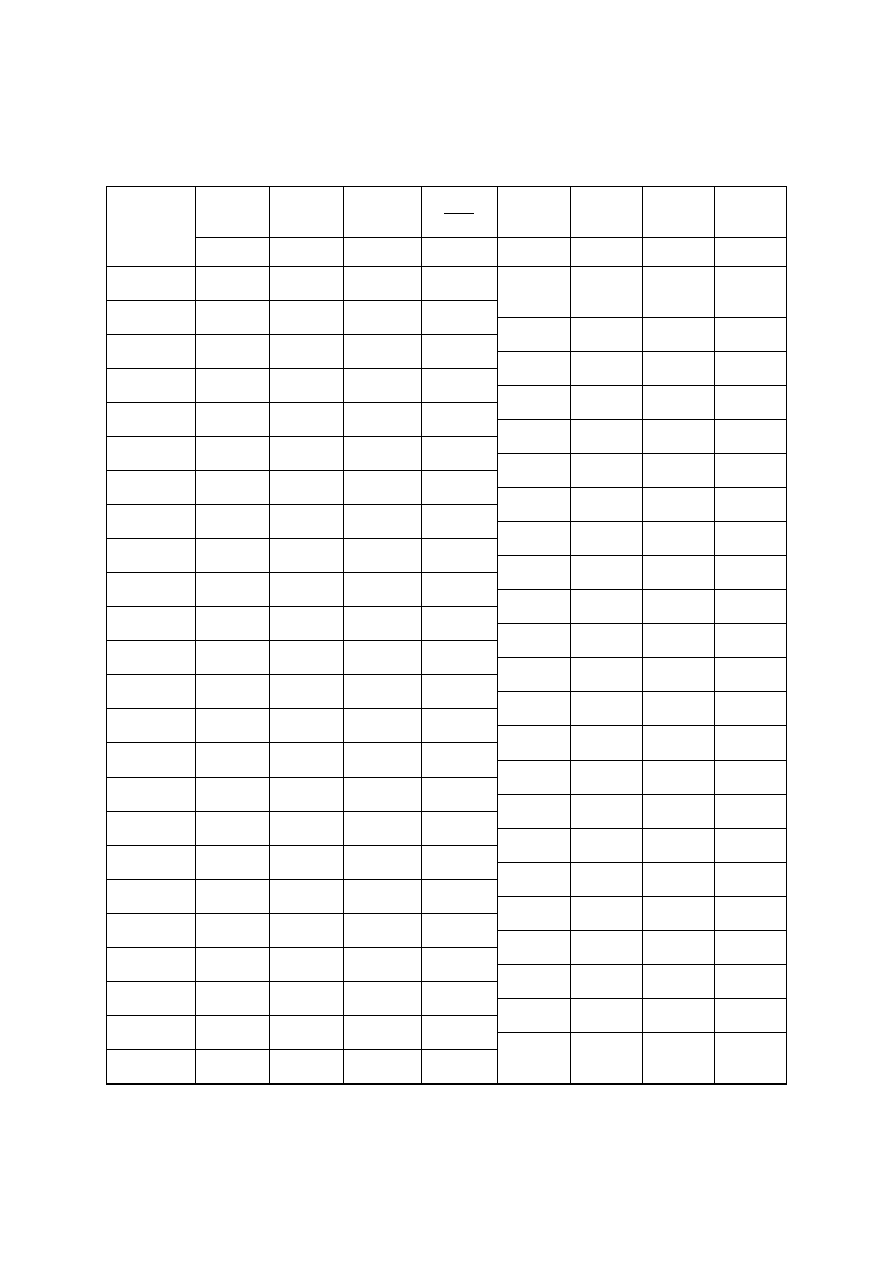
Wyniki pomiarów i obliczeń wydatku i położenia zwierciadła wody w piezometrach

Pomiar wydatku

Obniżenie zwierciadła wody w piezometrach [cm]

V

t

Q

Q

śr

Nr

pomiaru

[dm

3

]

[s]

[dm

3

/s] [dm

3

/s]

Odczyt

0 1 2 3 4 5 6 7 8 9 10 11 12 13

14

1

2

1

średnio

1

2

2

średnio

cd. tab. 2

Obniżenie zwierciadła wody w piezometrach [cm]

Nr

pomiaru

15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

1

2

22

Tabela 3

Wyniki obliczeń współczynników oporu przy przepływie w rurociągu

Q = ..................... [dm

3

/s], T = ....................... [

°C],

α = ......................... [– ]

d

i

v

i

Re

i

2g

αv

2

i

∆h

h

str

ζ

λ

Nr

piezometru

i

[cm] [cm/s] [

−]

[cm] [cm] [cm] [

−] [−]

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

23

cd. tab. 3

24

25

26

27

28

29

30

31

32

33

34

35

T – temperatura wody
α – współczynnik de Saint Venanta
∆h – różnica poziomów wody w kolejnych piezometrach
h

str

– wysokość strat energii między kolejnymi piezometrami

Część III. (Sz).Modelowanie filtracji przez zaporę ziemną

Schemat stanowiska pomiarowego i przebieg doświadczenia

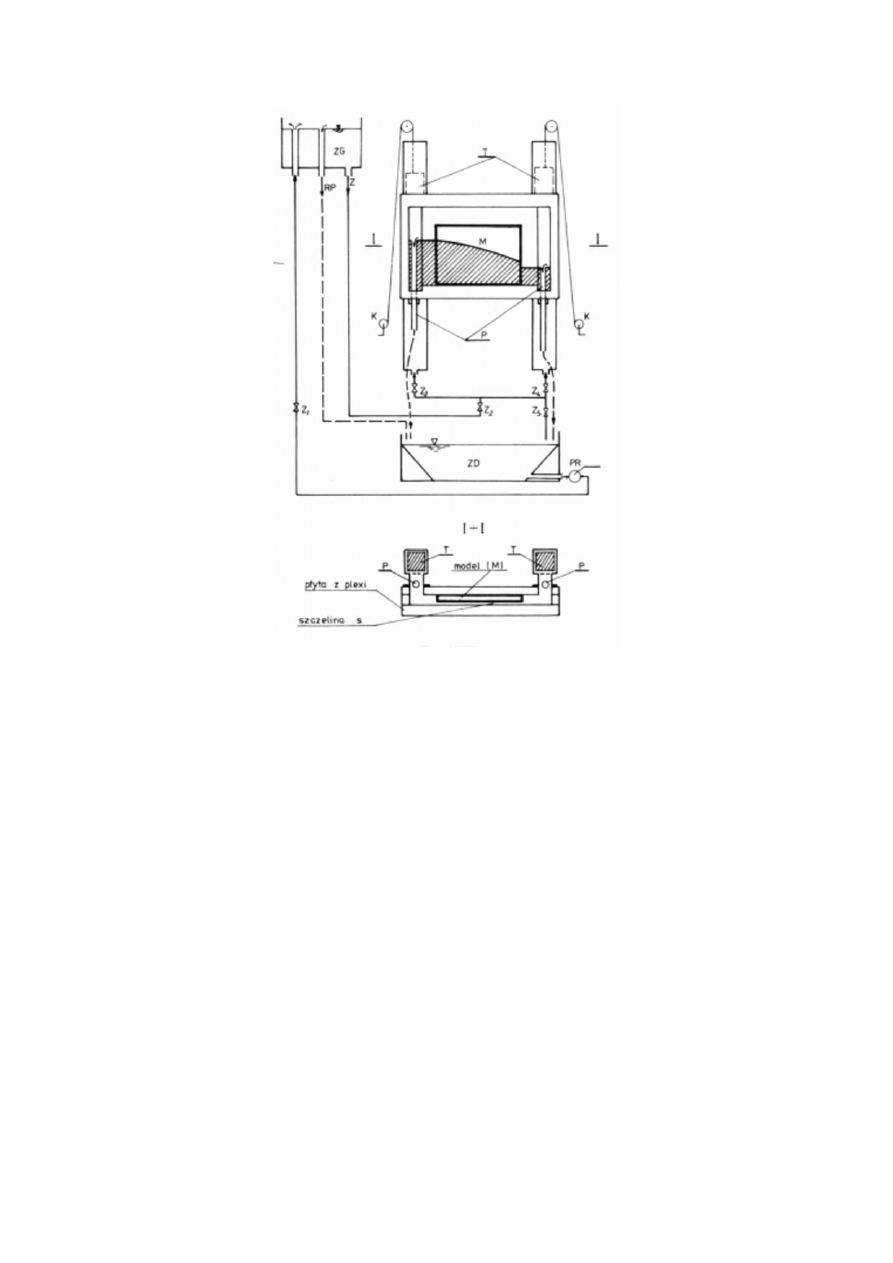
Stanowisko laboratoryjne (rys.12) tworzy model budowli piętrzącej np. grobli.

Pomiędzy dwoma płytami plexi możliwy jest przepływ oleju maszynowego. Szerokość
szczeliny została tak dobrana, aby bezwymiarowy współczynnik Reynoldsa spełniał
kryterium ruchu laminarnego w szczelinie. Zbiornika górny (ZG) napełniany jest pompą
ręczną przy otwartym zaworze (Z1). Nadmiar oleju w zbiorniku górnym przelewa się
rurociągiem powrotnym (RP). Doprowadzenie oleju do szczeliny odbywa się poprzez zawory
(Z2,Z3 i Z4). Poziom zwierciadła oleju po oby stronach grobli ustala się ręcznie ruchomymi
przelewami (P), poprzez ruch korb (K). Nadmiar oleju spływa do zbiornika dolnego (ZD).
Wszystkie ustawienia modelu wykonuje pracownik techniczny albo prowadzący zajęcia

.

Dla ustalonych warunków przepływu, zgodnie z rys. 9, należy odczytać wysokości
zwierciadła cieczy (h

0

oraz H) oraz długość rzutu zwierciadła wody w szczelinie na kierunek

poziomy (odległość L). Następnie dla 11 punktów odczytać odległość (s) oraz wysokość
zwierciadła cieczy (h

pom

).

24

Rys.12. Schemat stanowiska pomiarowego do ćwiczenia Sz.

Opracowanie wyników pomiarów

Dla każdego z punktów, w którym wykonano pomiary h

pom

, należy obliczyć wysokość

zwierciadła wody h

obl

(korzystając z relacji (26)), a następnie ocenić różnicę bezwzględną i

względną pomiarów i obliczeń. Wyniki pomiarów i obliczeń y zamieścić w tab. 4.

Dodatkowo należy sporządzić rysunek (z zachowaniem skali) odzwierciedlający

kształt zapory (grobli), warunki hydrauliczne po obu stronach zapory oraz układ teoretyczny i
rzeczywisty zwierciadła wody wewnątrz zapory.

25

Tab. 4

h

0

............... cm, H …………. cm, L …………. cm

Lp. odległość Wysokość zwierciadła cieczy

cm

Różnica bezwzględna

cm

Różnica względna

%

s h

pom

h

obl

obl

pom

h

h

h

−

=

∆

pom

h

h

∆

1 0

h

0

=

2

3

4

5

6

7

8

9

10

11 L=

H=

H=

0

0

4. Zawartość sprawozdania

Sprawozdanie powinno zawierać:

•

cel i zakres ćwiczenia;

•

krótki

wstęp teoretyczny dotyczący wszystkich części ćwiczenia;

•

opis poszczególnych części doświadczenia;

•

schematy stanowisk pomiarowych i krótki opis przebiegu pomiarów;

•

tabele z wynikami pomiarów i obliczeń;

•

przykłady obliczeń z przeliczeniem jednostek;

•

rysunek

układu linii ciśnienia i linii energii pomiędzy dwoma wybranymi piezometrami na

badanym odcinku rurociągu (o ile zaleci to prowadzący zajęcia);

•

rysunek

układu zwierciadeł wody (teoretycznego i pomierzonego) przy przepływie przez zaporę

ziemną;

•

wnioski

dotyczące wyników uzyskanych w poszczególnych częściach ćwiczenia, dotyczące m.in.:

- uzyskanych wartości krytycznych liczby Reynoldsa i ich zgodności z teorią dotyczącą

przejścia w przypadku przepływu pod ciśnieniem z ruchu laminarnego w turbulentny i
odwrotnie,

- uzyskanych wyników obliczeń współczynników oporu na tle ich przewidywanych wartości

teoretycznych,

- uzyskanych wartości strat energii na poszczególnych odcinkach rurociągu (o ile to możliwe –

wraz z komentarzem dotyczącym wpływu rodzaju materiału przewodu, rodzaju ruchu i typu
kształtek na uzyskane wartości strat energii);

- teoretycznego i rzeczywistego układu zwierciadła przy przepływie przez zaporę ziemną, wraz

z komentarzem dotyczącym słuszności założenia Dupuita.

Ewentualne inne wymagania dotyczące sprawozdania lub odstępstwa od proponowanej wyżej
zawartości sprawozdania zostaną przekazane grupom przez prowadzącego w trakcie zajęć.

26

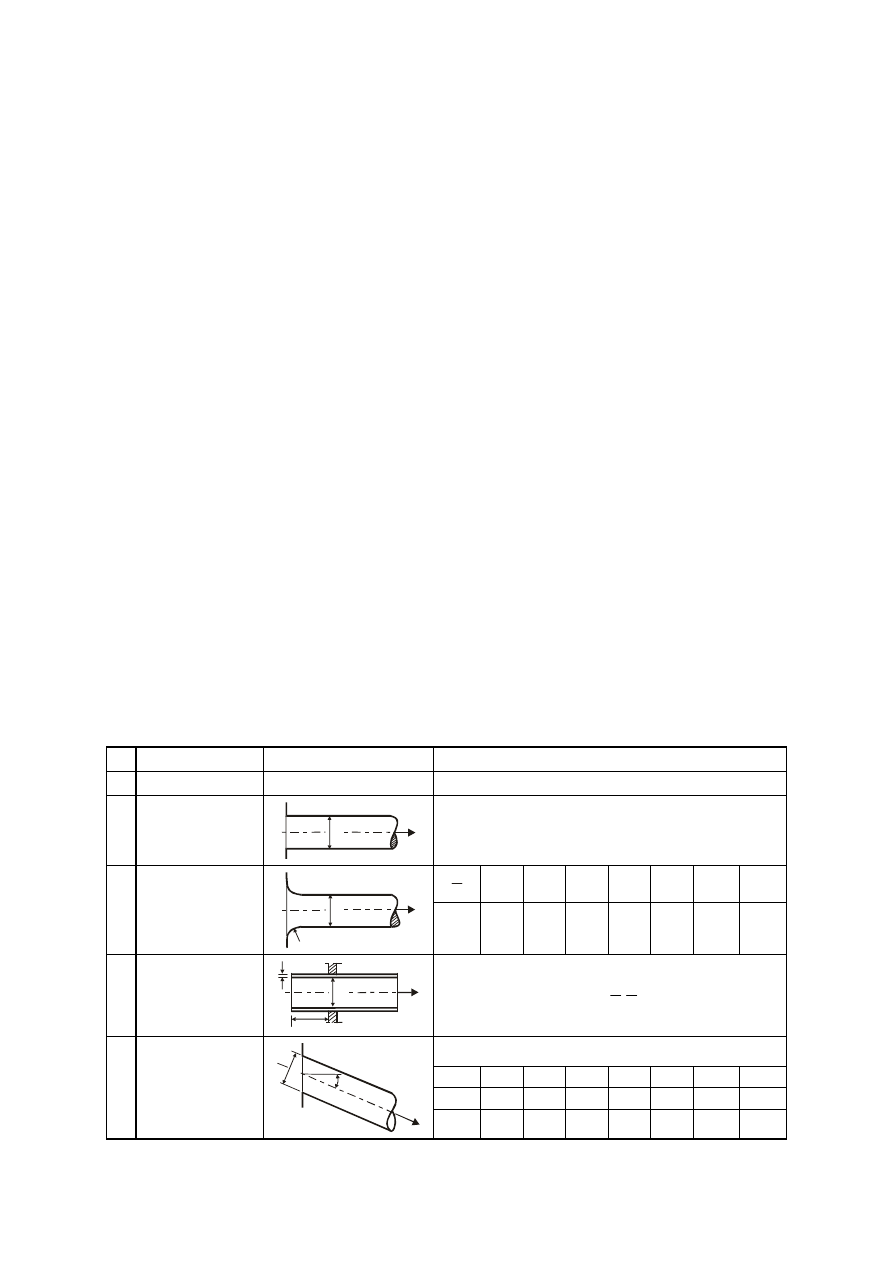
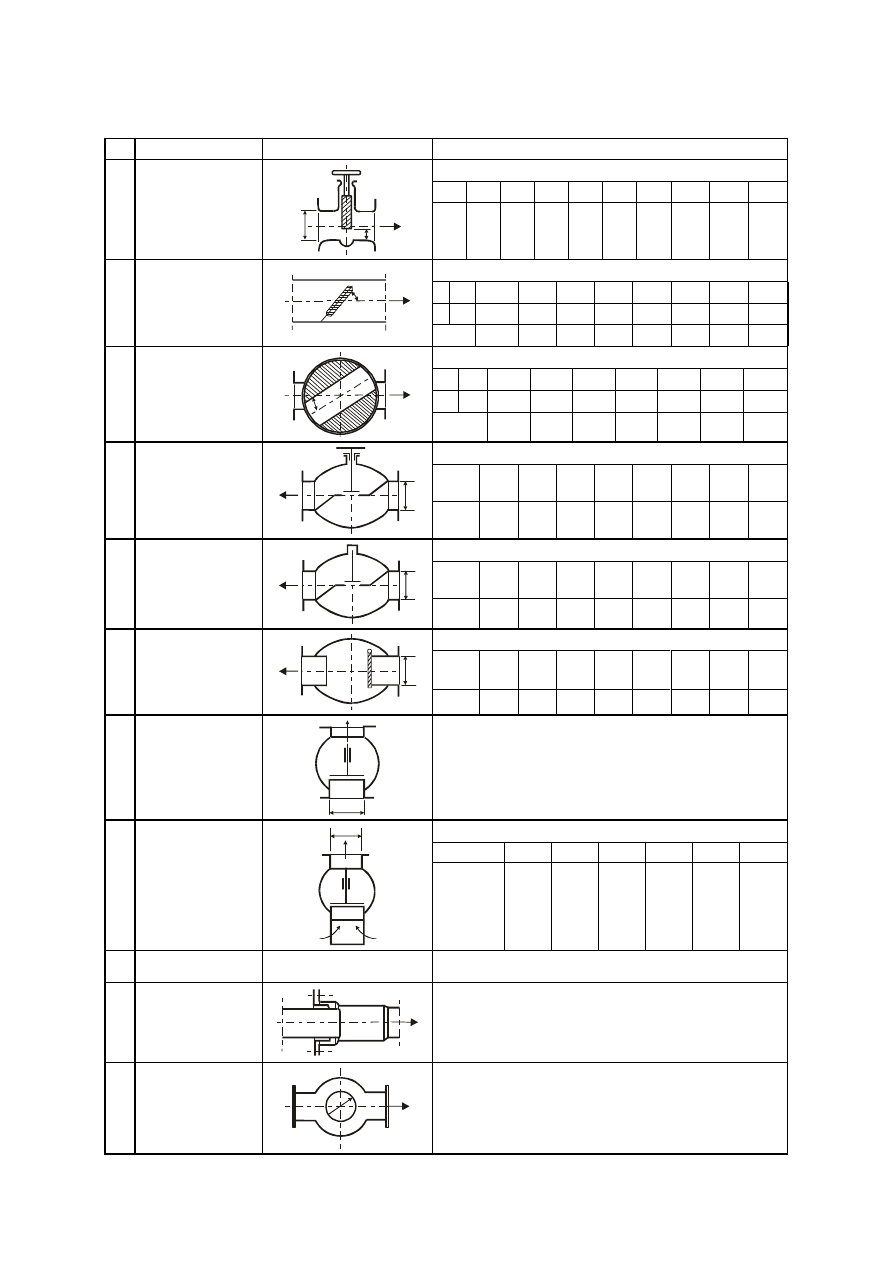
Załącznik 1

Współczynniki oporów lokalnych

Lp. Nazwa

przeszkody

Kształt

Współczynnik oporów miejscowych

ζ

1 2

3

4

1

Wlot o ostrych
krawędziach

D

v

0,5

D

r

0 0,01 0,02 0,05 0,10 0,16 0,20

2 Wlot

prosty

zaokrąglony

D

r

v

ζ

0,5 0,43 0,36 0,22 0,12 0,06 0,03

3

Wlot w rurę wsuniętą
przez otwór w ścianie
do wnętrza zbiornika

D

b

g

v

0

1

D

g

D

b

5

0

,

,

,

≤

⎟

⎠

⎞

⎜

⎝

⎛

ζ

=

ζ

≤

ϕ

⋅

+

ϕ

⋅

+

=

ς

2

sin

0,2

sin

3

0

5

0

,

,

º 10 20 30 45 60 70 80

Rd

π/18

π/9

π/6

π/4

π/3 7π/18 4π /9

4

Wlot do rury
pod kątem
(ze zbiornika)

D

v

ϕ

ζ

0,558 0,626

0,7 0,812 0,91 0,959 0,99

27

Zał.1 c.d.

1 2

3

4

5

Wlot z przewodu do
zbiornika

v

*

h

str

=

ζ

g

2

v

2

*

,

ζ = 1

*

v

− prędkość w przewodzie (przed przeszkodą)

2

2

1

2

1

D

D

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

ζ

2

1

2

D

D

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

1,2 1,4 1,6 1,8 2,0 2,5

ζ

0,04 0,16 0,36 0,64 1,0 2,25

2

1

2

D

D

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

3,0 3,5 4,0 5,0 6,0

6 Nagłe rozszerzenie

przekroju Re

≥ 3500

D

D

v

1

2

ζ

4,0 6,25 9,0 16,0 25,0

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

ζ

2

1

2

D

D

1

5

,

0

2

1

2

D

D

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

0,01 0,1 0,2 0,25 0,3 0,4 0,6 0,8

7 Nagłe zmniejszenie

przekroju

D

D

v

1

2

ζ

0,50 0,45 0,40 0,38 0,35 0,30 0,20 0,10

gładkie chropowate

°

15 45 60 90

90

ϕ

r/D

rd

5

π/6

π/4

π/3

π/2

π/2

1

0,03 0,14 0,19 0,21

0,51

2

0,03 0,09 0,12 0,14

0,30

4

0,03 0,08 0,10 0,11

0,23

6

0,03 0,075 0,09 0,09

0,18

8 Kolana

gięte

D

r

ϕ

v

10

0,03 0,07 0,07 0,11

0,20

°

15 30 45 60

90

ϕ

rd

5

π/6

π/6

π/4

π/3

π/2

S

1 2 2 3

3

ζ

0,06 0,10 0,15 0,20

0,25

9 Kolana

segmentowe

ϕ

v

S - liczba segmentów w kolanie

10 Kolana

półfaliste

v

ϕ

4

,

0

rd

2

=

ζ

π

=

ϕ

ζ = ζ(ϕ)

°

20 40 60 80 90 100

120

140 160

ϕ

rd 1/9

π 2/9π π/3 4/9π π/2 5/9π 2/3π 7/9π 8/9π

11 Załamanie przewodu

v

ϕ

ζ

0,04 0,14 0,36 0,74 0,98 1,26 1,86 2,43 2,85

28

cd. zał. 1

1 2

3

4

ζ = ζ(S/D)

S/D 0,25 0,30

0,4 0,5 0,6 0,7 0,8 0,9 1

12 Zawór

zasuwowy

równoprzelotowy

D

v

s

ζ

30 22 12 5,3 2,8 1,5 0,8 0,3 0,15

ζ = ζ(ϕ)

ϕ

°

10 20 30 40 50 60 70 90

rd 1/18

π 1/9π 1/6π 2/9π 5/18π 1/3π 7/18π 1/2π

13 Zawór

motylkowy

(klapowy, dławiący)

ϕ

v

ζ

0,52 1,54 3,91 10,8 32,6 118 751

∞

ζ = ζ(ϕ)

ϕ

°

10 20 30 40 50 55 67

rd 1/18

π

1/9

π 1/6π 2/9π 5/10π 0,96 1,17

14

Zawór kurkowy (kurek

gazowy)

ϕ

v

ζ

0,31 1,84 6,15 20,7 95 275

∞

ζ = ζ (D)

D

[mm]

20 40 80 100

150 200 250 300

15 Zawór

grzybkowy

normalny

v

D

ζ

8,0 4,9 4,0 4,1 4,4 4,7 5,1 5,4

ζ = ζ (D)

D

[mm]

25 32 40 50 80 100 150 200

16 Zawór

zwrotny

grzybkowy normalny

v

D

ζ

4,5 4,8 5,3 6,0 7,4 7,6 6,0 4,5

ζ = ζ(D)

D

[mm]

25 32 40 50 80 100 150 200

17 Zawór

zwrotny

klapowy

v

D

ζ

1,9 1,6 1,5 1,4 1,3 1,2 0,9 0,8

18 Zawór

zwrotny

grzybkowy osiowy

D

v

ζ = ζ (D)= 2,2 ÷ 2,5

ζ = ζ (D)

D[mm] 40 70 100 200 300 500

19

Kosz z zaworem
zwrotnym

D

v

ζ

12 8,5 7,0 4,7 3,7 2,5

20

Kosz bez zaworu
zwrotnego

ζ = 0,9 ÷ 6 w zależności od konstrukcji kosza

21 Kompensator

dławikowy

v

ζ ≅ 0,2

22 Wodomierz

v

Tłoczkowy

ζ = 12

Płytkowy

ζ = 8

Skrętowy

ζ = 6

29