ZASTOSOWANIE OPORNIKA TERMOMETRYCZNEGO Pt 100 DO POMIARU

TEMPERATURY.

Cel ćwiczenia:

Pokazanie możliwości:

•

cyfrowego pomiaru wielkości nieelektrycznej przy użyciu przetworników o nieliniowej
charakterystyce przetwarzania,

•

minimalizacji błędów wynikających z aproksymowania nieliniowej funkcji przetwarzania funkcją
liniową,

•

zastosowania programowanych przyrządów pomiarowych,

•

wykorzystania w technice pomiarowej mostków niezrównoważonych.

Program ćwiczenia:

1.PARAMETRY PRZETWORNIKA Pt 100
1.1.Zapoznać się z parametrami przetwornika termometrycznego Pt 100 (norma PN - 83 /M.-53852).
1.2.Wyznaczyć maksymalną nieliniowość czujnika Pt 100 w określonym przedziale temperatur T

min

-

T

max

.

1.3.Wyznaczyć temperaturę otoczenia z bezpośredniego pomiaru rezystancji czujnika .
2.PRZYSTOSOWANIE PROGRAMOWANEGO MULTIMETRU V563 DO POMIARU
TEMPERATURY W ZAKRESIE T =0

o

C do T= T

max

.

(Zakres pomiarowy powinien zawierać temperaturę otoczenia).
2.1 Wyznaczyć równanie prostej T = AR

T

+C, przechodzącej przez 2 punkty : P1( R

min

, T

min

),

P2( R

max

,T

max

), gdzie (T

min

, T

max

) określa zakres programowanego termometru.

2.2. Zaprogramować multimetr V563 współczynnikami prostej wyznaczonej w p. 2.1
2.3.Sprawdzić doświadczalnie zgodność wskazań utworzonego termometru z mierzoną temperaturą.
(Zmiany temperatury symulować zmianą wartości rezystancji opornicy dekadowej zgodnie z
charakterystyką przetwornika Pt 100 daną w normie).Obliczyć bezwzględne błędy aproksymacji i
wyznaczyć wartość błędu maksymalnego odniesionego do zakresu przetwarzania (T

max

- T

min

).

2.4.Zmierzyć zaprogramowanym multimetrem, współpracującym z czujnikiem Pt100 temperaturę
otoczenia.
2.5.Sprawdzić jak na wynik pomiaru temperatury otoczenia wpływa długość kabli łączących multimetr z
czujnikiem. Pomiary wykonać dla 2 i 4 przewodowego połączenia z miernikiem. Wyjaśnij przyczynę
rozbieżności.
2.6.Zaproksymować wyznaczoną doświadczalnie funkcję przetwarzania T = f (R) prostą, która zapewni
mniejsze błędy wskazań utworzonego termometru. Określić maksymalny błąd aproksymacji.
3.PRZYSTOSOWANIE NIEZRÓWNOWAŻONEGO MOSTKA CZTERORAMIENNEGO DO
POMIARU TEMPERATURY.

3.1.Zrównoważyć mostek dla R

T

=100

Ω

i napięcia zasilania mostka U

AB

= 1V.

3.2.Dobrać doświadczalnie napięcie zasilające mostek tak, aby dla skrajnych wartości z założonego
zakresu (T

min

, T

max

) projektowanego termometru i rezystorów stosunkowych równych R

2

= R

3

=100

Ω

( 1000

Ω

, 10000

Ω

), miliwoltomierz cyfrowy, mierzący napięcie rozrównoważenia mostka, wskazywał

wartości U

CDmin

=(1mV/

o

C)*T

min

oraz U

CDmax

= (1mV/

o

C)* T

max

.

3.3.Zmierzyć napięcie rozrównoważenia mostka w funkcji zmian temperatury (zmiany temperatury
modelować zmianami rezystancji).W badanym zakresie wykonać kilkanaście pomiarów równomiernie
rozłożonych w założonym zakresie temperatury. Pomiary wykonać przy następujących wartościach
oporników stosunkowych R

2

= R

3

= 100

Ω

(1000

Ω

, 10000

Ω

).

3.4.Wyznaczyć graficznie charakterystyki U

CD

= f (T), oraz błąd ∆T = f (T) wynikający z nieliniowości

charakterystyk U

CD

= f (T) dla zadanych wartości oporników stosunkowych. 3.5.Zmierzyć temperaturę

otoczenia czujnikiem PT100 współpracującym z mostkiem niezrównoważonym. Sprawdzić jak na wynik
pomiaru temperatury wpływa długość kabli łączących czujnik z mostkiem..
3.6.Aproksymować wybraną charakterystykę U

CD

= f (T) prostą minimalizującą błąd nieliniowości ∆T.

Określić dla jakich wartości T

1

i T

2

błąd ∆T przyjmuje wartość zero.

3.7.Dobrać warunki pracy mostka tak, aby dla rezystancji odpowiadających temperaturom T

1

i T

2

napięcie rozrównoważenia mostka odpowiadało wartościom U

CD1

= 1mV/

o

C)*T

1

oraz U

CD2

=

(1mV/

o

C)* T

2

.

3.8.Zmierzyć napięcie rozrównoważenia tak wykalibrowanego mostka w funkcji zmian temperatury.

UWAGA

NA ĆWICZENIA NALEŻY PRZYNIEŚĆ KALKULATOR, NAJLEPIEJ INŻYNIERSKI, I
PAPIER MILIMETROWY

Uwagi do wykonania ćwiczenia

Ad.2.2. Na wyposażeniu stanowiska znajduje się multimetr V563, który umożliwia matematyczną
obróbkę wyników pomiaru w pięciu programach. W ćwiczeniu użyteczny jest program skalowania (P2),
który przelicza wynik pomiaru x na wartość y zgodnie zależnością:

•

y =Ax+C;

gdzie A i C parametry, których wartość wprowadzana jest z klawiatury . Odpowiadają one wyznaczonym
współczynnikom a i b prostej aproksymującej.
Patrz instrukcja obsługi multimetru rozdział 6. Programowanie multimetru.
Obliczenia prowadzone są z dokładnością do 8 cyfr a wynik obliczeń podawany w tzw. notacji naukowej
(E c = 10

C

). Tak duża dokładność obliczeń jest przyczyną tego, że niewielkie przypadkowe zmiany

wielkości mierzonej powodują zmianę ostatnich cyfr wyniku , utrudniając odczyt; dlatego wskazane
zastosowanie programu uśredniania wyników (program 6, opcja 1) dzięki czemu uśrednione zostaną
przypadkowe zmiany wyniku pomiaru.
Temperaturę mierzoną należy symulować wartościami rezystancji opornicy dekadowej. Opornica
dekadowa pozwala na regulację R z ziarnem 0,1 Ω. Zatem maksymalna różnica między wartością podaną
w tabeli charakterystyki przetwornika a wartością ustawioną na opornicy wynosi 0,05 Ω co powoduje
błąd symulacji temperatury około 0,1

0

C. Błąd symulacji można zminimalizować po uprzednim

przedstawieniu charakterystyki czujnika w postaci funkcji T=f (R) uporządkowanej dla wartości R,
zadawanych w przedziale zmian (R

min

, R

max

) z określonym krokiem, np. 2

Ω

.

Ad.3.1. Przed przystąpieniem do pomiarów w układzie mostkowym należy usunąć z pamięci multimetru
program stosowany do skalowania omomierza. Sprawdzić, czy woltomierz jest “wyzerowany”. Dołączyć
do mostka woltomierz, napięcie zasilające i jako R

T

opornicę dekadową symulującą T. Ustawić w

ramionach mostka wartości rezystancji, zapewniające równowagę mostka dla temperatury T=0

0

C (R

T

=

R

4

= 100 Ω i R

2

= R

3

). Ustawienie w ramionach mostka rezystancji o wartościach spełniających warunek

równowagi mostka nie gwarantuje, że napięcie rozrównoważenia mostka wyniesie U

CD

= 0. Jeśli

miliwoltomierz nie wskazuje zera mV należy zmieniać wartość rezystora regulacyjnego R

4

w mostku do

momentu zrównoważenia mostka. Drugi punkt , w którym wskazanie miliwoltomierza U

CDmax

=

(1mV/

o

C)* T

max

, należy uzyskać regulując napięcie zasilania mostka po ustawieniu wartości R

T

odpowiadającej wartości T

max

. Zakres miliwoltomierza dobrać tak, aby wynik pomiaru temperatury

podawany był z dokładnością do 0,1 C

0

. Sprawdzić, czy po zmianie napięcia zasilania spełniony jest

warunek U

CD

= 0 dla R

T

=100

Ω

.Pomiary powtórzyć dla różnych wartości R

2

= R

3

.

Ad.3.6.Spełnienie warunku U

CD1

= (1mV/

o

C)*T

1

oraz U

CD2

= (1mV/

o

C)* T

2

wymaga kilkakrotnej

regulacji. Należy ustawić na rezystorze symulującym wartość mierzonej temperatury wartość
odpowiadającą temperaturze T

1

i regulować rezystor R

4

mostka tak, aby uzyskać wskazanie

U

CD1

=(1mV/

o

C)*T

1

, następnie ustawić na rezystorze symulującym wartość rezystancji odpowiadającej

temperaturze T

2

i regulować napięcie zasilania mostka tak, aby U

CD2

=(1mV/

o

C)*T

2

; sprawdzić

wskazanie miliwoltomierza dla T

1

w razie potrzeby doregulować R

4

; kolejno sprawdzić wskazanie

miliwoltomierza dla T

2

w razie potrzeby doregulować napięcie zasilania. Czynności te powtarzać do

momentu uzyskania zgodności wskazań U

CD1

= (1mV/

o

C)*T

1

oraz U

CD2

= (1mV/

o

C)* T

2

.

Optymalizację prostej aproksymującej przeprowadzić metodą graficzną , po narysowaniu charakterystyki
U=f(R), a następnie wykorzystać metodę najmniejszych kwadratów, wspomaganą kalkulatorem z
odpowiednim oprogramowaniem lub arkusz kalkulacyjny EXCEL.

Wprowadzenie do tematu

Oporniki termometryczne.
Oporniki termometryczne są stosunkowo często stosowane do pomiaru temperatury metodami
elektrycznymi. Są to oporniki , których rezystancja zależy od temperatury. Zależność ta jest opisana
funkcją nieliniową . Charakterystyki oporników termometrycznych podawane są w formie tabelarycznej i
analitycznej (norma PN - 83 /M.-53852).

Nieliniowość charakterystyki R = f (T) oraz fakt, że dla temperatury T= 0

o

C rezystancja czujnika Pt 100

wynosi 100Ω utrudnia skalowanie układu mierzącego rezystancję bezpośrednio w stopniach Celsjusza.
Programowane przyrządy

Jednym ze sposobów skalowania miernika w

°

C jest zastosowanie do pomiaru rezystancji

programowanego omomierza. Przyrządy cyfrowe umożliwiają często wewnętrzną obróbkę wyników
pomiarów. Program obliczeń wprowadzany jest za pomocą klawiatury przyrządu. Z reguły w
programowanym przyrządzie można zastosować przeliczanie wyniku pomiaru x na wartość y według
zależności liniowej y=ax+b. Zastosowanie przyrządu, który można przeskalować zgodnie z zależnością
y=ax+b pozwala na poprawne przesunięcie punktu zerowego, ale wynik pomiaru obarczony jest
dodatkowo tzw błędem aproksymacji wynikającym z aproksymacji funkcji nieliniowej funkcją liniową..
Często odstępstwo charakterystyki przetwornika od funkcji liniowej nazywane jest błędem nieliniowości.
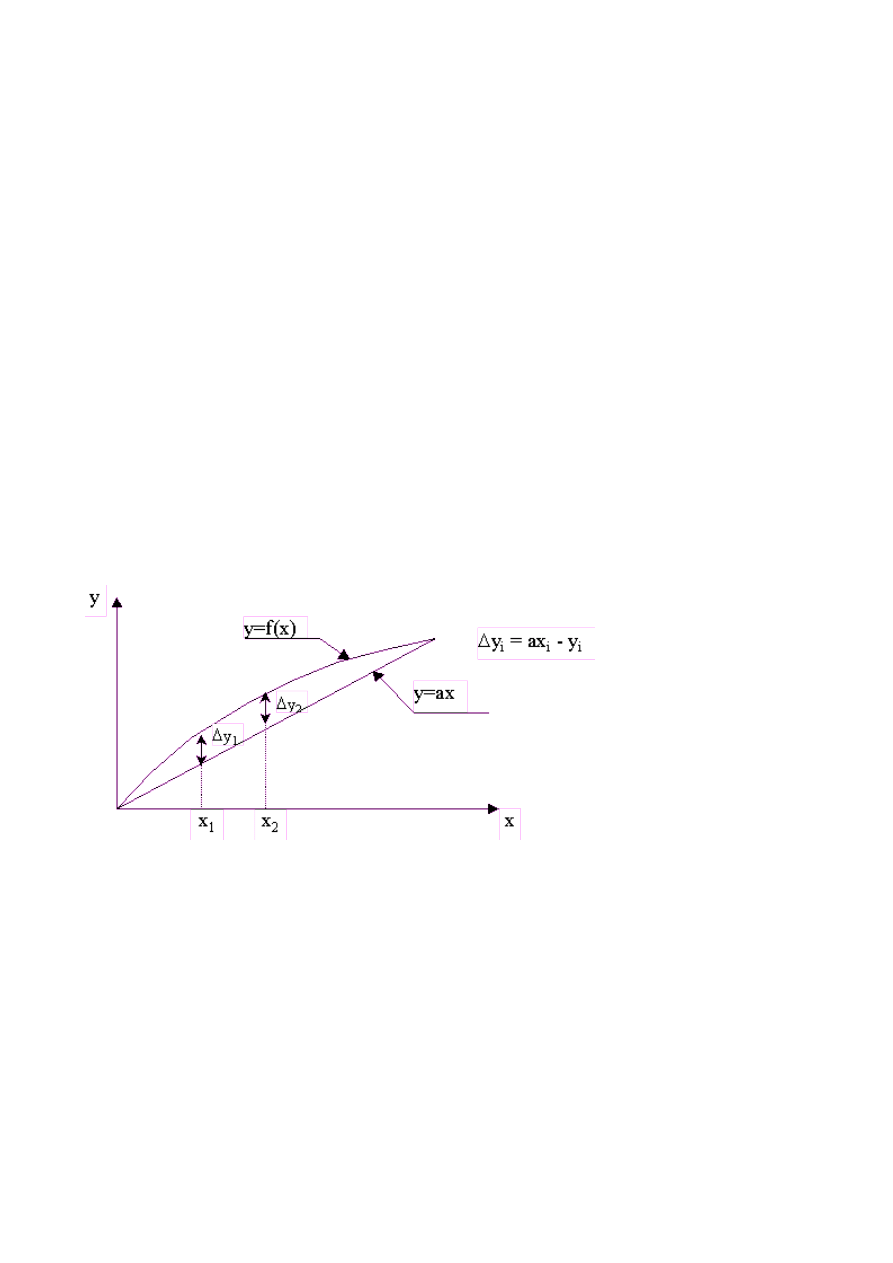
(wartość błędu aproksymacji odpowiada wartości błędu nieliniowości). Ilustrację błędu aproksymacji
(nieliniowości) podano na rys. 1

Rys.1 Nieliniowa charakterystyka y=f(x) przetwornika i aproksymująca ją prosta y=ax
Mając do dyspozycji programowany omomierz , który można przeskalować zgodnie z funkcją
T=A*R+C należy wyznaczyć współczynniki A i C tak, aby wynik cyfrowy odpowiadał wartości
mierzonej temperatury dla dwóch wybranych temperatur np. T = 0

0

i T = T

max

.Tak przeskalowany

przyrząd wskazywać będzie wartości T = 0

0

i T = T

max

z błędem wynikającym z niedokładności czujnika

(przetwornika Pt 100) i z niedokładności omomierza . Pozostałe wartości z przedziału 0

0

do T

max

obarczone będą dodatkowo błędem wynikającym z nieliniowości charakterystyki T = f(R). Minimalizację
błędu pochodzącego z nieliniowości charakterystyki można uzyskać aproksymując funkcję T = f(R) inną
prostą (rys.2b)

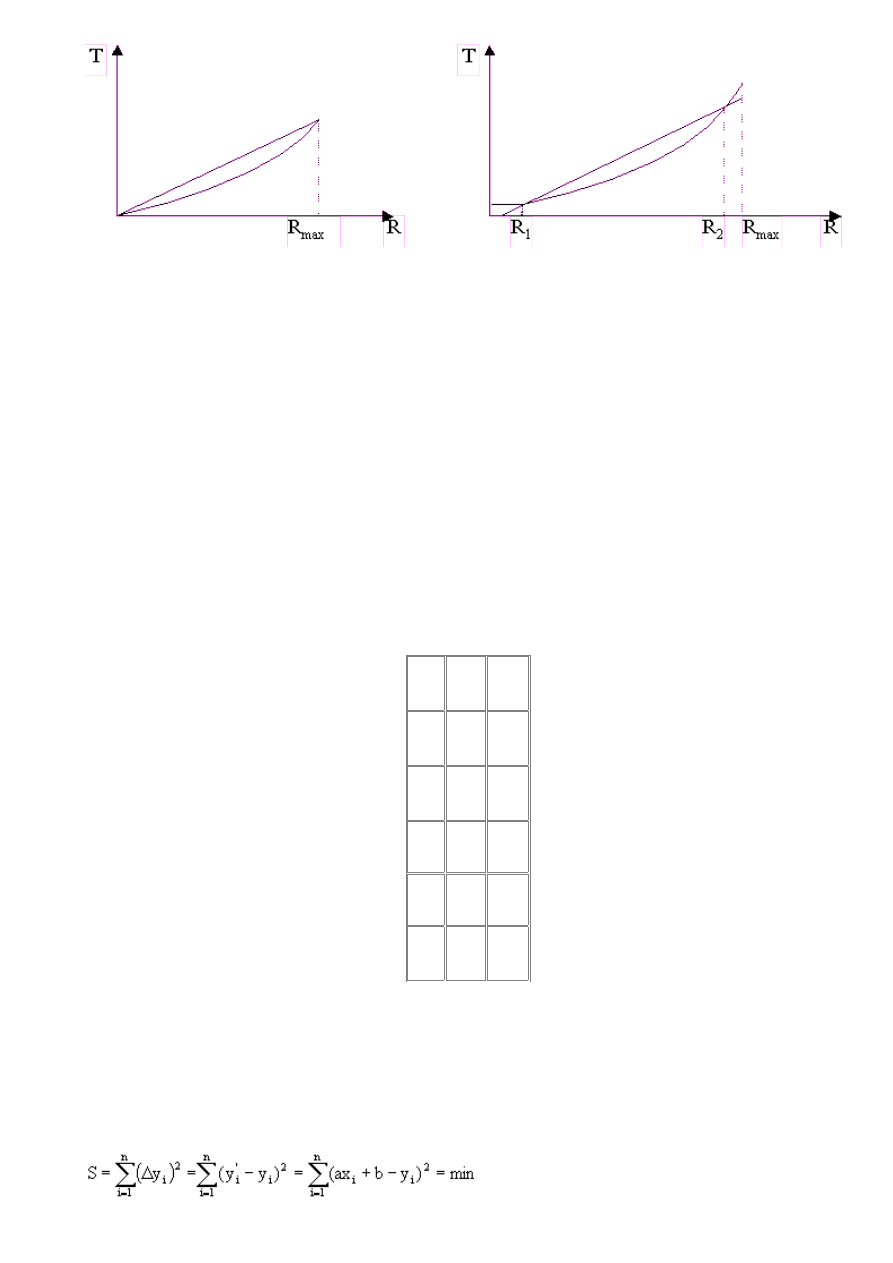
Rys.2
a - Aproksymacja charakterystyki nieliniowej prostą łączącą punkty wyznaczające zakres pomiarowy.
b - Aproksymacja charakterystyki nieliniowej prostą minimalizującą błąd nieliniowości.
Współczynniki prostej minimalizującej błąd nieliniowości można wyznaczyć w przybliżeniu metodą
graficzną lub dokładniej, wykorzystując funkcję regresji liniowej, wykorzystującą tzw. metodę
najmniejszych kwadratów.
Metoda najmniejszych kwadratów
Metoda najmniejszych kwadratów (najmniejszej sumy kwadratów błędów) jest powszechnie stosowana
do wyznaczania analitycznej postaci funkcji opisującej zależność wielkości wyjściowej obiektu od
wartości wejściowych na podstawie wyników pomiaru tych wielkości.
Zasadę zobrazujemy ograniczając funkcję szukaną do funkcji liniowej y=ax+b czyli zastosujemy metodę
regresji liniowej.
Załóżmy, że chcemy obliczyć współczynniki a i b prostej, która najmniej różni się od charakterystyki
obiektu dla którego dane są w postaci n par (y

i

, x

i

)

wyniki pomiarów (tabela 1).

Tab.1 Pary wyników x

i

,

yi

i

x

i

y

i

1

x

1

y

1

2

x

2

y

2

.

.

.

.

.

.

n

x

n

y

n

Metoda najmniejszych kwadratów pozwala na obliczenie współczynników a i b które gwarantują,
że suma kwadratów S różnic między wartościami y’ obliczonymi z zależności :

y’= ax

i

+b a wartościami y

i

jest minimalna. Różnica

∆

y

i

=y

i

’-y

i

jest błędem aproksymacji.

Warunek minimalizacji sumy S kwadratów różnic między wartościami zmierzonymi i wyliczonymi czyli
błędów aproksymacji, przyjmuje postać:

(1)

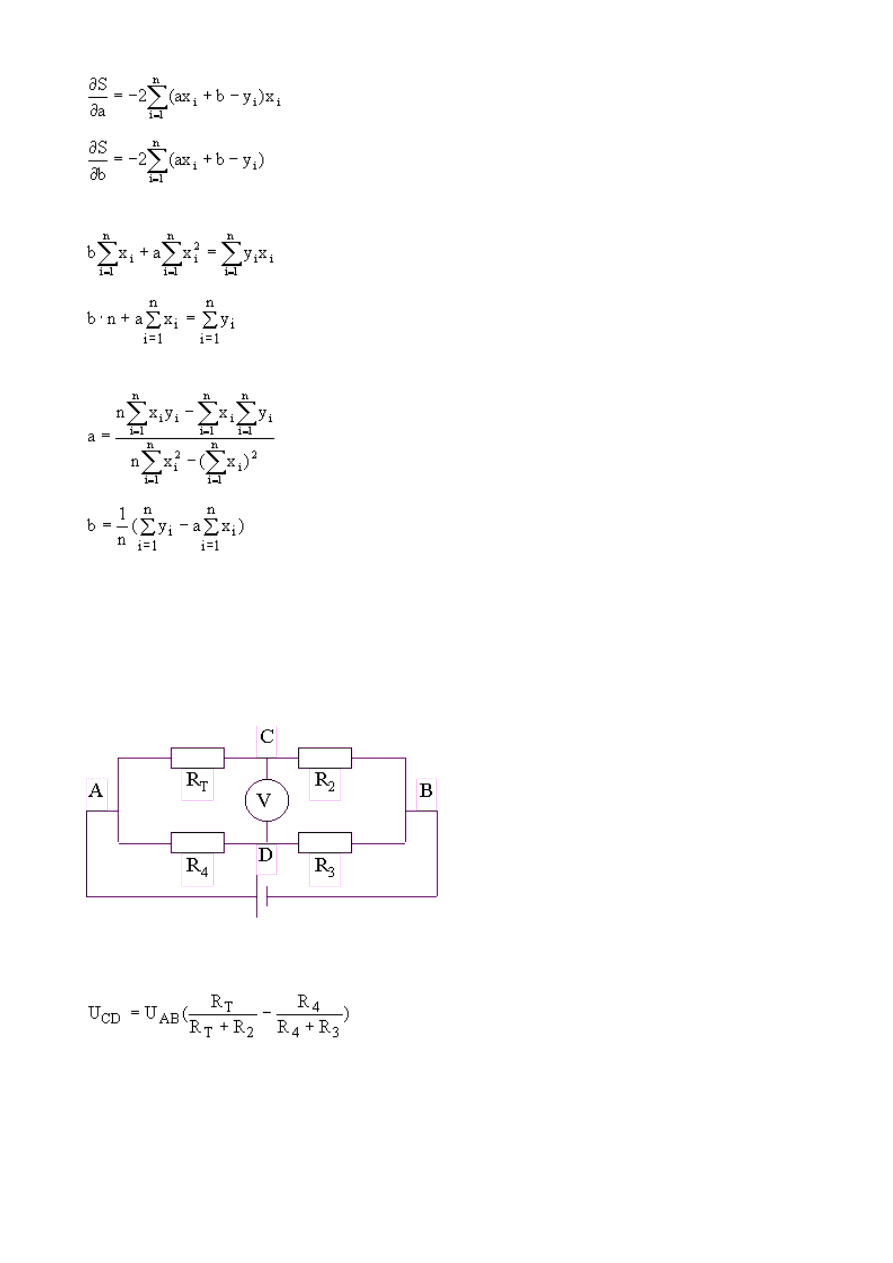
Aby zminimalizować S względem a i b należy wyznaczyć pochodne cząstkowe

(2)

(3)

Po przyrównaniu pochodnych cząstkowych do zera otrzymuje się układ równań

(4)

(5)

Z warunków 4 i 5 wyznacza się współczynniki a i b

(6)

(7)

Do obliczenia współczynników regresji liniowej a i b można wykorzystać kalkulator inżynierski lub
funkcję regresji w arkuszu Excela.
Niezrównoważony mostek Wheatstone’a
Do pomiaru temperatury za pomocą oporników termometrycznych stosuje się często niezrównoważony
mostek Wheatstone`a (rys. 3).

Rys.3 Schemat mostka Wheatstone’a
Napięcie U

CD

określone jest następującą zależnością:

(8)

Jeśli R

T

= R

4

i R

2

= R

3

to napięcie U

CD

= 0 i mostek jest w stanie zrównoważnia. Zmiana R

T

(oporności

czujnika), przy niezmienności pozostałych rezystorów mostka, spowoduje pojawienie się napięcia
rozrównoważenia (U

CD

≠

0) (mostek jest niezrównoważony). Napięcie rozrównoważenia mostka U

CD

jest

nieliniową funkcją R

T

. O kształcie charakterystyki U

CD

= f (T) decyduje nieliniowość U

CD

= f (R

T

) oraz

nieliniowość charakterystyki R

T

= f (T). Można tak dobrać warunki pracy mostka, że napięcie U

CD

będzie miało wartość 0 mV dla T=0

0

i wartość U

CDmax

= (1mV/

o

C)* T

max

(rys.4).

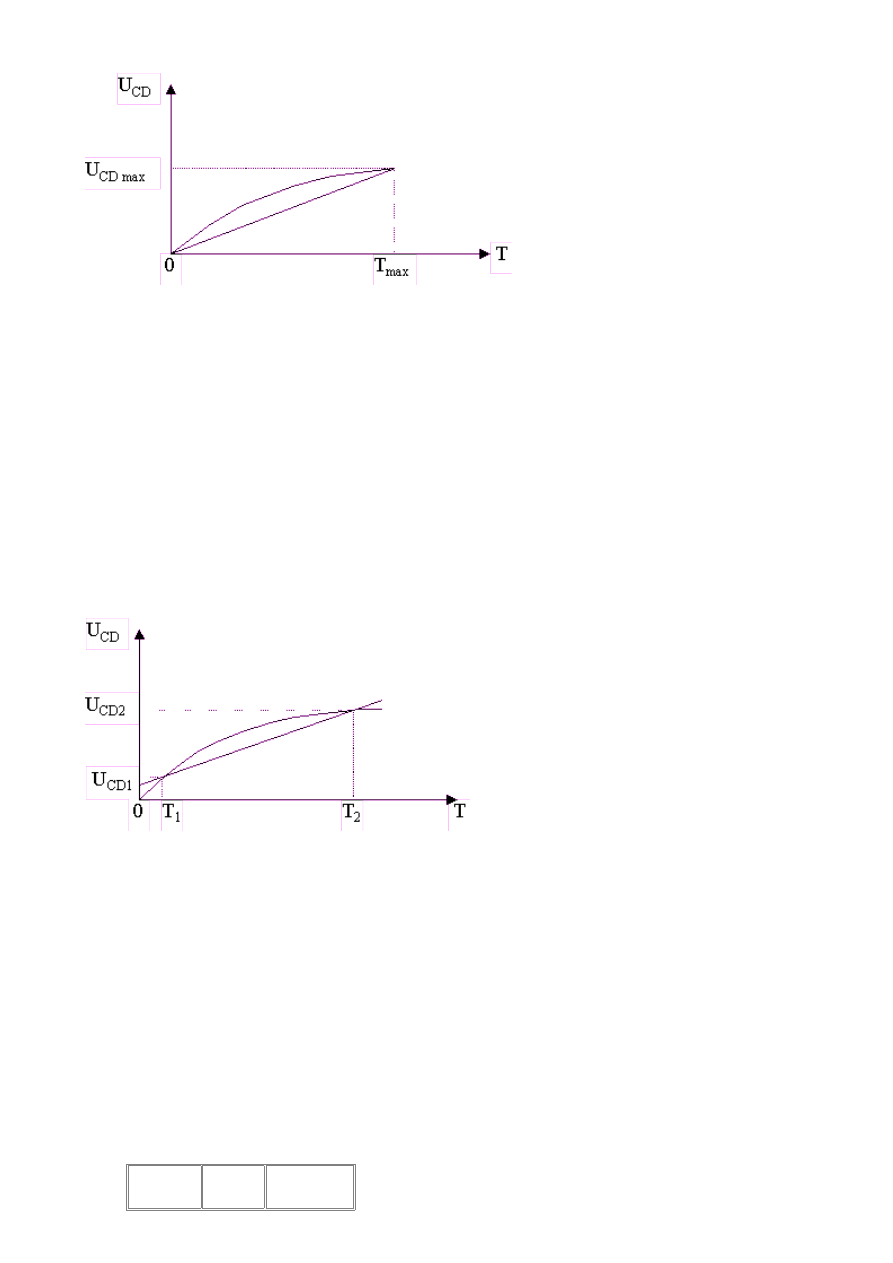
Rys.4 Charakterystyka U

CD

= f (T) i jej aproksymacja prostą przechodzącą przez punkty

T=0

0

i T = T

max

0

.

Wskazania woltomierza mierzącego napięcie rozrównoważenia mostka można traktować jako wynik
pomiaru temperatury. Utworzony w ten sposób termometr poprawnie wskazuje wartości T = 0

0

i T =

T

max

0

(z błędem wynikającym z symulowania temperatury przez rezystor R

T

); pozostałe wartości

obarczone są dodatkowo błędem wynikającym z nieliniowości charakterystyki U

CD

= f (T).

Minimalizację tych błędów można uzyskać aproksymując rzeczywistą funkcję przetwarzania U

CD

= f(T)

inną prostą, dla której termometr wskaże poprawnie inne wartości niż T

min

oraz T

max

. (rys. 5) a

maksymalna różnica temperatury między wartością rzeczywistą mierzonej temperatury a odczytaną ze
wskazań miliwoltomierza będzie mniejsza. Do wyznaczenia parametrów tej prostej można także
zastosować funkcję regresji liniowej i metodę najmniejszych kwadratów.

Rys.5 Charakterystyka U

CD

= f (T) i jej aproksymacja prostą przechodzącą przez punkty T=T

1

oraz T = T

2

.

Pytania i zadania.

1. Wyznacz analityczną zależność U

CD

= f(R

T

) dla mostka jak na rysunku 1.

2. Dobierz napięcia zasilania mostka (rys. 3)tak aby przy pomiarze temperatury 50

0

C, woltomierz

wskazywał wartość napięcia 50mV . Rezystancja przetwornika Pt 100 w temperaturze 50

0

C

wynosi 119,40 Ω a rezystancja R

4

= 100Ω , R

2

= R

3

= 1000Ω.

3. Dlaczego woltomierz mierzący napięcie U

CD

może wskazywać napięcie różne od zera chociaż we

wszystkich gałęziach mostka znajdują się oporniki o nominalnej wartości 100Ω ?

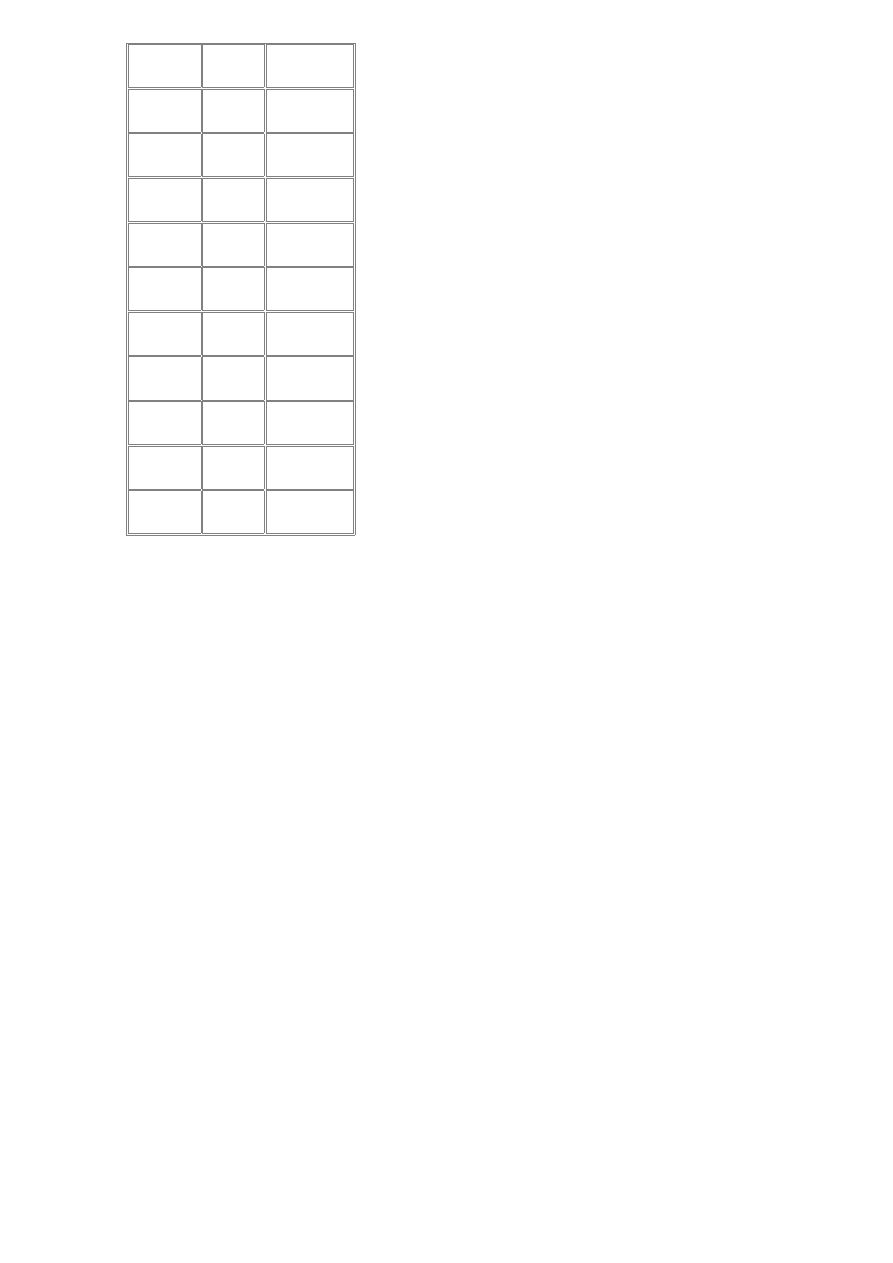
4. Dla podanych w tabeli par wyników oblicz współczynniki prostej spełniającej warunek minimum

sumy kwadratów różnic między wynikami pomiarów a wartością obliczoną z równania prostej.
Sprawdź czy możnaby przyjąć, że badana charakterystyka jest charakterystyką liniową jeśli
wiadomo, że wielkość wyjściowa zmierzona była z błędem δ = ±0,5%y.

lp

x

y

1

0

67,08

2

5

70,89

3

10

75,20

4

15

79,53

5

20

83,92

6

25

87,87

7

30

92,40

8

35

97,01

9

40

100,88

10

45

105,74

11

50

110,49

5. Jaki błąd, wynikający z niezerowej rezystancji doprowadzeń, popełnimy przyjmując wskazania
omomierza za wartość rzeczywistą mierzonej rezystancji, jeśli R

x

wynosi około 10Ω a rezystancja

doprowadzeń około 40mΩ. Zaproponuj układ pomiarowy lub sposób dołączenia rezystora do omomierza
pozwalający na eliminację wpływ rezystancji doprowadzeń na wynik pomiaru.