Wahadło torsyjne
Pomiar modułu sztywności drutu stalowego metodą
dynamiczną
Ćw.3
Cel ćwiczenia
Zapoznanie się z teorią odkształceń ciał. Prawo Hooke'a. Doświadczalne wyznaczanie modułu sztywności
stali.
Zakres obowiązującego materiału teoretycznego
Drgania harmoniczne. Dynamika ruchu obrotowego. Moduł sztywności.
Przyrządy użyte w doświadczeniu
Wahadło obrotowe (wahadło torsyjne) oraz krążek dodatkowy. Do przeprowadzenia pomiaru potrzebny jest
sekundomierz, śruba mikrometryczna, suwmiarka, linijka.
Podstawy teoretyczne
a) Współczynnik sztywności
W przypadku odkształceń sprężystych, w których siła jest przyłożona stycznie do powierzchni (siła ścinająca),
wartość odkształcenia mierzona kątem α zależy od stosunku siły F do powierzchni S wg prawa Hooke'a:
S
F
G
1
=
α
(1)
Współczynnik G nazywamy współczynnikiem (lub modułem) sztywności.
b) Skręcanie drutu
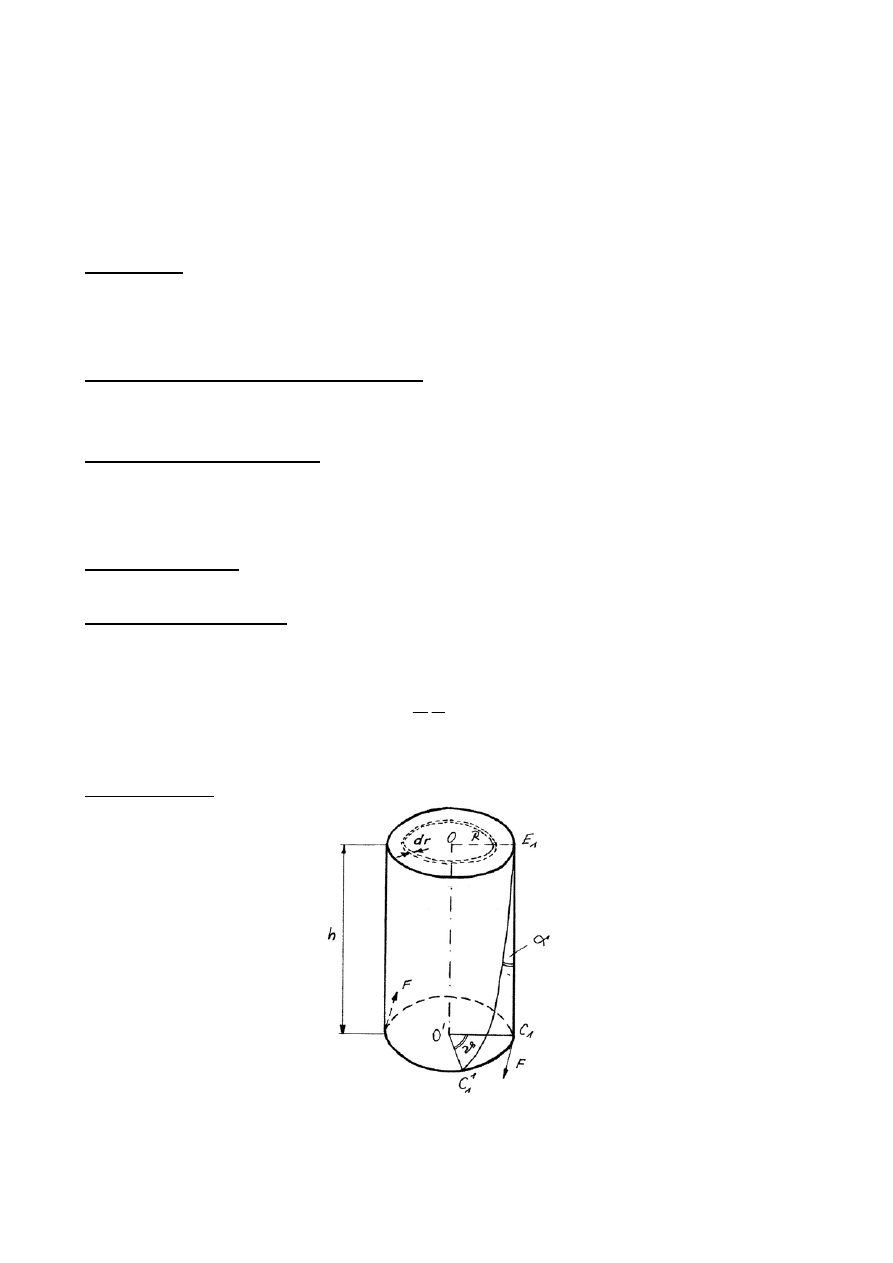
Rys.1
1
Rozważmy walec kołowy o wysokości h i promieniu R (rys.1), którego jedna podstawa O jest osadzona trwale,
druga natomiast O' podlega działaniu pary sił o momencie N równoległym do walca. Walec doznaje skręcenia,
podstawa O' obraca się o kat ϑ. Rozpatrzmy obecnie jakąś tworzącą walca np. odcinek prostej E
1
C
1
, który
przekształca się w odcinek spirali E
1
C
1
'
. Odkształcenie tego odcinka wyraża się katem obrotu α
h
r
h
C
C
tg
'
1
1
ϑ
=
=
α
(2)
Dla małych kątów tgα = α, zatem
h
r
ϑ
=
α
jest miarą odkształcenia
Z prawa Hooke'a:(1)
dS
G
dF
α
=
Moment dN tej siły względem osi OO' wynosi
rdS
G
rdF
dN
α
=
=
Pole powierzchni zawarte miedzy kołami o promieniu r i r + dr równa się dS = 2πrdr
Obliczamy N:
∫
π
ϑ
=
R
0
rdr
2
r
h
r
G
N
∫
ϑ
π
=
ϑ
π
=
R
0
4
3
h
2
GR
dr
r
h
G
2
N
(3)
albo
ϑ
= C
N
gdzie
h
2
GR
4
π
=
C
(4)
Moment pary sił skręcenia jest proporcjonalny do kata skręcenia ϑ.
Drgania torsyjne
Drgania torsyjne jakiegoś ciała stałego posiadającego swobodę obrotu dookoła osi OO' powstają
wówczas, gdy siły przyłożone do tego ciała mają względem osi moment wypadkowy, który dąży do
przywrócenia ciału jego stanu pierwotnej równowagi. Gdy moment ten jest proporcjonalny do kata ϑ, o
który ciało zostało obrócone, drgania torsyjne są podobne do drgań harmonicznych a ich równanie ruchu
ma postać.
0
C
dt
d
J
2
2
=
ϑ
+
ϑ
(5)
gdzie J jest momentem bezwładności ciała względem osi obrotu.
Rozwiązaniem tego równania jest wzór na zależność kąta skręcenia ϑ od czasu.
2
t
sin
0
ω
ϑ
=
ϑ
(6)
ω - częstość drgań;
J
C
2
=
ω
ϑ
o
- amplituda skręcenia
ω
π
=
2
T
- okres drgań;
C
J
2
T
π
=
(7)
Zasada pomiaru współczynnika sztywności
Opisane drgania torsyjne można wywołać w drucie sprężystym osadzonym jednym końcem w uchwycie, jeżeli
na drugim jego końcu zawiesimy krążek metalowy o momencie bezwładności J
o
, którego ciężar będzie napinał
drut.
Jeśli chcemy wyznaczyć wartość współczynnika sztywności materiału z którego zrobiony jest drut, wprawiamy
drut w drgania torsyjne. Wyznaczywszy okres drgań T, ze wzoru (7), wyznaczamy C:
2
0
2
T
J
4
C
π
=
(8)
Podstawiając za C wyrażenie ze wzoru (4) otrzymujemy
2
0
2
4
T
J
4
h
2
GR
π
=
π
po przekształceniu
4
2
0
R
T
h
J
8
G
π
=
(9)
J
o
jest momentem bezwładności krążka wraz z drutem, którego wartości nie znamy i nie możemy obliczyć.
W celu wyeliminowania tej wartości, po wyznaczeniu wartości T dla jednego krążka, nakładamy na ten
krążek inny krążek o dającym się wyznaczyć momencie bezwładności J i wyznaczamy powtórnie okres
drgań T
1
.
C
J
2
T
0
π
=
,
C
J
J
2
T
0
1
+
π
=
C
J
4
T
0
2
2
π
=
,
C
J
J
4
0
2
2
1
+
π
=
T
Odejmujemy te równania stronami
C
J
4
T
T
2
2
2
1
π
=
−
wobec tego
3
(
)
4
2
2
1
R
T
T
Jh
8
G
−
π
=
(10)
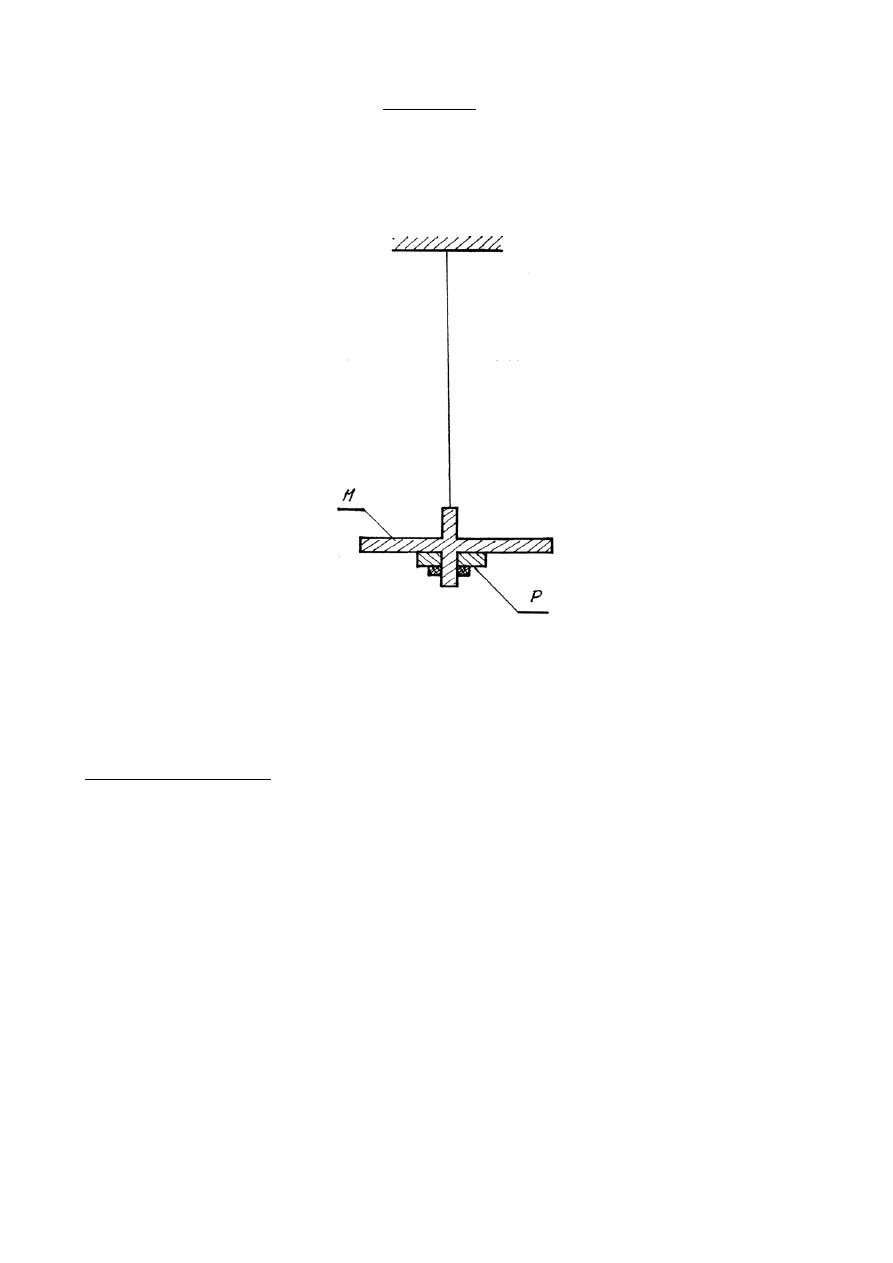
Do pomiaru współczynnika sztywności stali używamy drutu o średnicy 2R i długości około 100cm. Górny koniec
tego drutu osadzony jest w uchwycie, dolny zaś umocowany jest w osi metalowego walca zakończonego
metalowym krążkiem M (rys.2)
Rys.2
Do krążka metalowego można dołożyć (przykręcić od spodu) jeszcze jeden krążek P o dającym się
wyznaczyć momencie bezwładności J.
Przeprowadzenie pomiaru
a. Wyznaczyć pięć razy średnice drutu 2R za pomocą śruby mikrometrycznej. Obliczyć wartość średnią.
b. Wyznaczyć pięć razy długość drutu h za pomocą miarki milimetrowej. Obliczyć wartość średnią.
c. Wyznaczyć pięć razy średnicę zewnętrzną pierścienia dodatkowego 2R
1
za pomocą suwmiarki. Obliczyć
wartość średnią.
d. Wyznaczyć pięć razy średnicę wewnętrzną pierścienia dodatkowego 2R
2
za pomocą suwmiarki. Obliczyć
wartość średnią.
e. Masa krążka dodatkowego m = 800
±
5g.
f. Wyznaczyć pięć razy po 20 okresów T dla układu o momencie bezwładności J
o
. Obliczyć wartość średnią
dla jednego okresu.
g. Wyznaczyć pięć razy po 20 okresów T
1
dla układu o momencie bezwładności J
o
+J. Obliczyć wartość
średnią dla jednego okresu.
h. Obliczyć moment bezwładności krążka dodatkowego według wzoru:
4
(
)
2
2
2
1
R
R
m
2
1
J
+
=
(11)
i. Obliczyć współczynnik sztywności G według wzoru (10)
j. Przeprowadzić rachunek błędów. Określić błędy mierzonych wielkości: ∆R, ∆h, ∆R
1
, ∆R
2
, ∆T, metoda
Studenta-Fischera (Instrukcja nr 17).
Przykład obliczania błędu dla wielkości x (x reprezentuje wielkości R, h, R
1
, R
2
, T):
błąd pomiaru wielkości x
1
n
S
t
x
−
=
∆
α
gdzie:
S - odchylenie standardowe wyrażone wzorem:
(
)
n
x
x
S
n
1
i
2
i
∑
=
−
=
x
- wartość średnia wielkości x wyliczona ze wzoru:
n
x
x
n
1
i
i
∑
=
=
x
i
- i-ty pomiar wielkości x;
n - liczba pomiarów;
α - poziom istotności α=0,05;
t
α
- współczynnik Studenta odczytany z tablic (instrukcja Nr 17) dla r=n-1 stopni swobody;
Wynik pomiaru wynosi:
x
x
x
∆
±
=
Błąd względny pomiaru wynosi:
%
100
x
x
x
∆
=
∆
k. Błąd bezwzględny współczynnika sztywności ∆G liczymy metoda różniczki zupełnej (instrukcja nr 17):
∆
+
−
∆
+
∆
+
∆
=
∆
R
R
4
T
T
T
2
h
h
J
J
G
G
1
(12)
l. Błąd względny współczynnika sztywności wynosi:
%
100
G
G
G
∆
=
∆
5
m. Wartość błędu względnego ∆J/J wyliczyć należy metoda różniczki zupełnej (instrukcja nr 17) w oparciu o
wzór 11:
2
2
2
1
2
1
R
R
)
R
R
(
R
2
m
m
J
J
+
+
∆
+
∆
=
∆
(13)
n. Wyniki obliczeń i wnioski. Na osobnej stronie podąć wyniki obliczeń momentu bezwładności i
współczynnika sztywności z uwzględnieniem błędów. Napisać wnioski.
6