Politechnika Gdańska
Wydział Elektrotechniki i Automatyki
Katedra Inżynierii Systemów Sterowania
Sterowanie Procesami Ciągłymi
Laboratorium termin T3
Materiały pomocnicze – regulator LQR
Opracowanie:
Mieczysław A. Brdyś, prof. dr hab. inż.
Wojci
ech Kurek, mgr inż.
Gdańsk, październik 2009
Sterowanie Procesami Ciągłymi
Polecenie do Laboratorium T2
2
W przypadku sterowania opartego na sprzężeniu od stanu obiektu, kluczowe dla jakości
działania układu jest odpowiednie wybranie położenia biegunów układu zamkniętego.
Umożliwia to uzyskanie zadowalającej dynamiki układu zamkniętego.
Niestety podejście oparte o ręczny wybór położenia biegunów układu zamkniętego nie
zapewnia optymalności otrzymanego układu. W tym celu został opracowany regulator
optymalny z kwadratowym wskaźnikiem jakości (LQR). Podejście to umożliwia określenie
optymalnej macierzy sprzężenia od stanu K umożliwiającej minimalizacje następującej
funkcji kosztów.
0
2
T
T
T
V
x
t Qx t
u
t Ru t
x
t Nu t
dt
Gdzie macierze
,
Q R
są diagonalnymi macierzami wag umożliwiającymi zmianę wpływu
poszczególnych zmiennych stanu i sterowao na przedstawione kryterium jakości. Natomiast
N
jest dodatkową macierzą umożliwiająca uwzględnienie wpływu sterowania na stan
układu przy projektowaniu macierzy sprzężenia od stanu. Zostanie ona pominięta w tym
przypadku.
Dla przykładu układ z trzema zmiennymi stanu i dwoma wejściami wymagałby podania
poniższych macierzy wag.
1
1
2
2
3
0
0
0
0
0 ,
0
0
0
r
Q
R
r
Odpowiedni dobór macierzy wag ma kluczowe znaczenie dla działania układu
wykorzystującego regulator LQR, ponieważ dobierając wagi można określid który
stan/sterowanie jest dla osoby projektującej regulator ‘droższy’ i dobrze byłoby
zminimalizowad jego wartości nawet kosztem pogorszenia pozostałych.
W tym przypadku prawo sterowania otrzymuje postad
u
Kx
Gdzie K opisane jest następującym wyrażeniem
1
T
T
K
R
B P
N
W celu wyznaczenia macierzy P należy rozwiązao ciagłe równanie Riccatiego w postaci
1
0
T
T
T
A P
PA
PB
N R
B P
N
Q
Można w tym celu wykorzystad proste polecenie Matlaba lqr. Jego składnia jest następująca:
Sterowanie Procesami Ciągłymi
Polecenie do Laboratorium T2
3
[K, P, eig]=lqr(A, B, Q, R, N)
Gdzie
K jest macierzą sprzężenia od stanu
P jest rozwiązaniem przedstawionego powyżej równania Riccatiego
Eig jest położeniem biegunów układu zamkniętego
A jest macierzą stanu układu
B jest macierzą wejśd układu
Q, R i N są macierzami wag.
Przykład
Jako przykład wykorzystania sterowania LQR wykorzystany zostanie dobrze Paostwu znany
układ wahadła z tłumieniem. Układ opisany jest następującym równaniem różniczkowym.
2
2
2
2
sin
d
g
d
dt
ml
l
ml
dt
Zlinearyzowany układ opisany jest następującymi równaniami stanu
x
Ax
Bu
y
Cx
Gdzie macierze opisujące otrzymany układ są następujące
0
1
0
1
0
,
,
9,81
1
5
0
1
A
B
C
Następnie przeprowadzono symulacje dla dwóch różnych macierzy wag stanu Q.
1
0
,
1
0
0,1
Q
R
Oraz
1
0
,
1
0
1
Q
R
Jak widad zmiana wagi odpowiedzialnej za drugą zmienna stanu w kryterium jakości działania
regulatora miała znaczący wpływ na przebiegi przejściowe prędkości kątowej wahadła (druga
zmienna stanu).
Dla pierwszego przypadku macierz sprzężenia od stanu miała postad
4,164 1,144
K
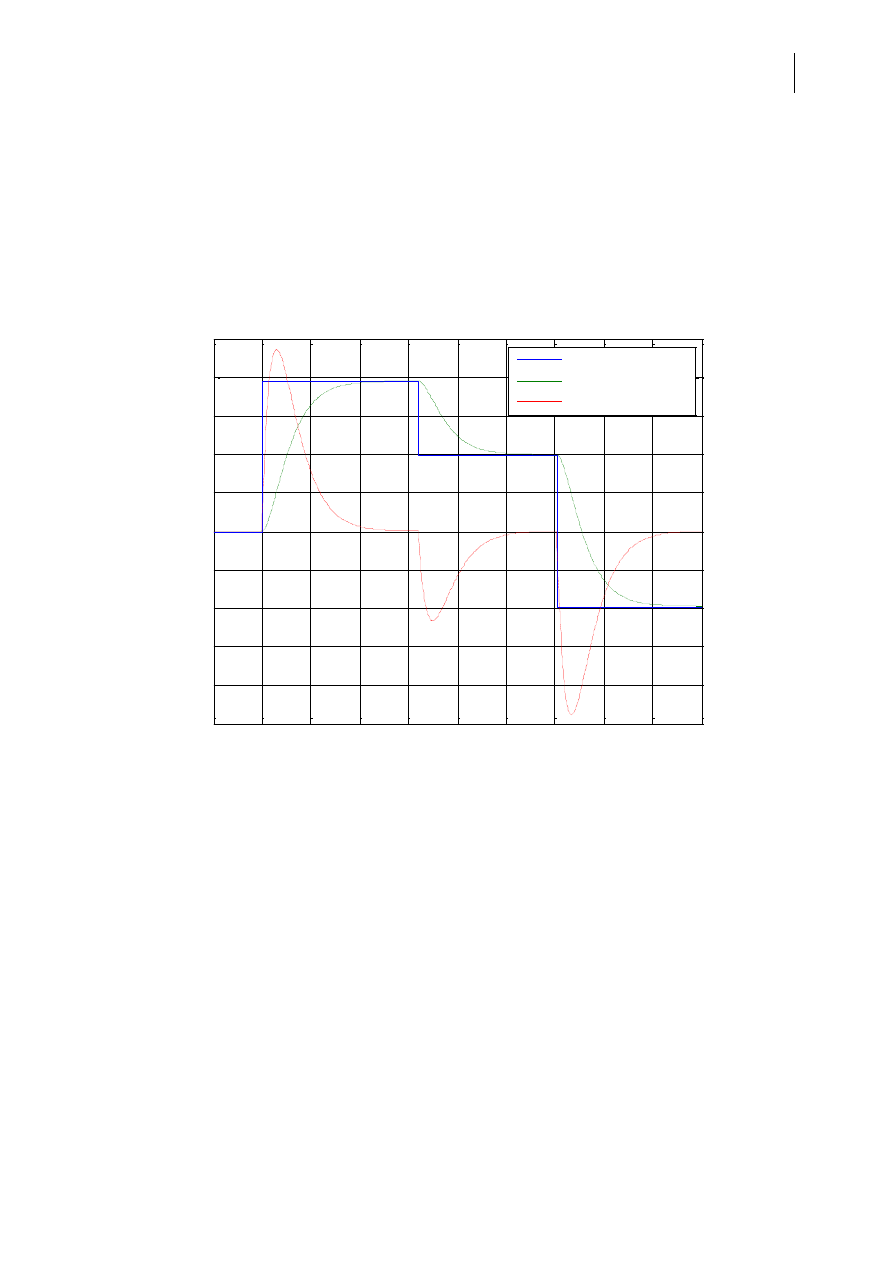
Sterowanie Procesami Ciągłymi
Polecenie do Laboratorium T2
4
Dla tak dobranej wartości macierzy sprzężenia od stanu bieguny układu zamkniętego są następujące
1
2
3,88;
2,835
Dodatkowo została jeszcze wyznaczona macierz feedforward w celu umożliwienia realizacji wartości
zadanej przez prezentowany układ.
2, 2021
r
F
0
1
2
3
4
5
6
7
8
9
10
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
Czas [s]
Ro1 = 1, Ro2 = 0.1
Polozenie zadane
Polozenie wahadla
Predkosc wahadła
Sterowanie Procesami Ciągłymi
Polecenie do Laboratorium T2
5
0
1
2
3
4
5
6
7
8
9
10
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
Czas [s]
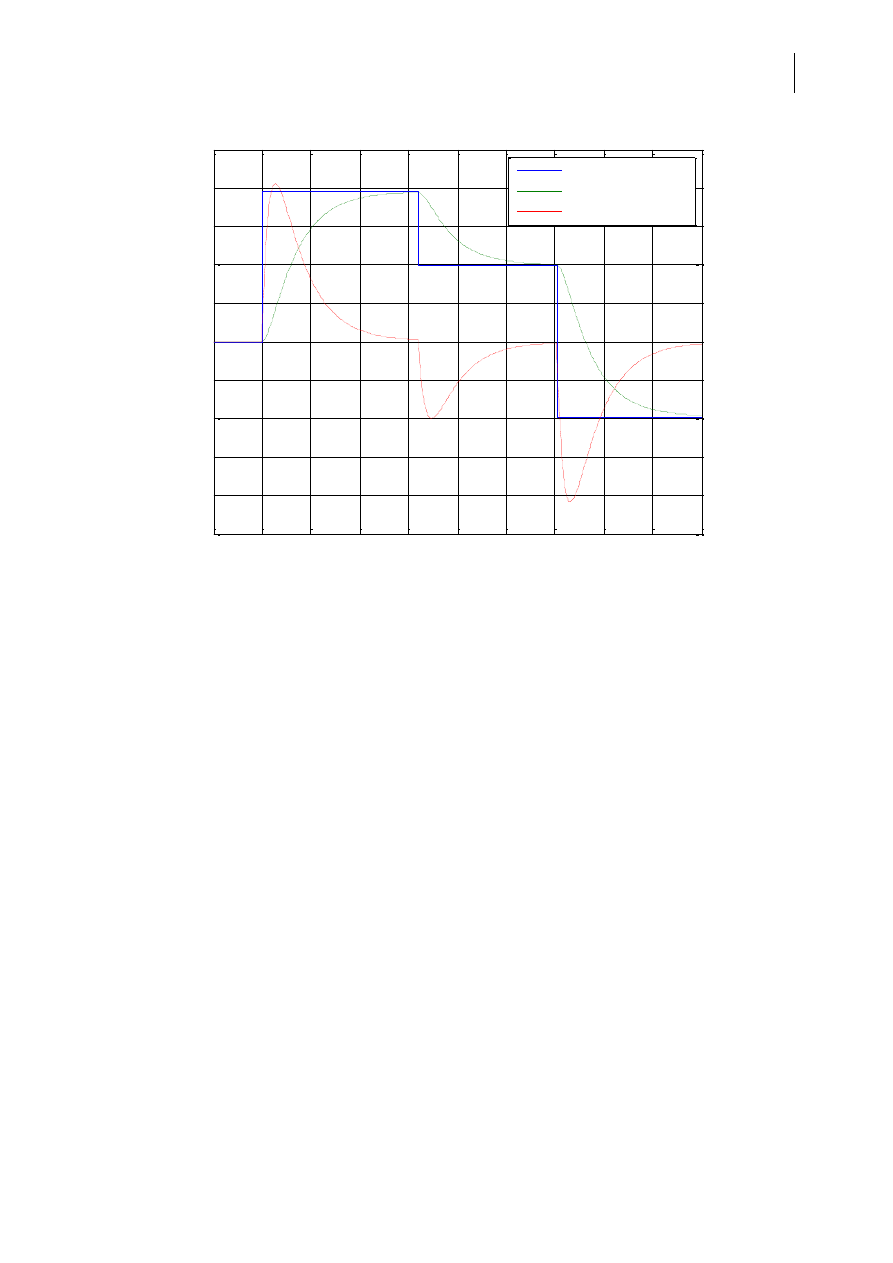
Ro1 = 1, Ro2 = 1
Polozenie zadane
Polozenie wahadla
Predkosc wahadła