Moduł 5a Projektowanie ścieżki dezinflacyjnej
Działania Europejskiego Banku Centralnego mają przede wszystkim na celu
stabilizację poziomu cen w okresie długim.
Europejski Bank Centralny dośd często korzysta z
takiej postaci reakcji, która mocno nawiązuje do klasycznej reguły Taylora (1993, 1999). Można ją
zapisad w sposób następujący:
t
t
t
t
y
y
R
i
gdzie:
0
,
t
i
- krótkookresowa stopa procentowa (instrument polityki Banku Centralnego),
R – poziom długookresowej realnej stopy procentowej (jest on stały, wówczas nominalna
długookresowa stopa procentowa jest sumą stopy realnej r oraz celu inflacyjnego
, który także jest
stały),
t
- stopa inflacji,
t
y
- stopa wzrostu bieżącej wielkości produkcji zagregowanej,
y
- stopa wzrostu wielkości zagregowanej produkcji potencjalnej.
Jak wynika z równania powyżej, Bank Centralny powinien zmienid poziom stopy procentowej
t
i
, jeżeli stopa inflacji odchyli się od poziomu celu inflacyjnego lub jeśli zmieni się rozmiar tzw. luki
popytowej, tj. różnicy pomiędzy bieżącym a potencjalnym poziomem zagregowanej produkcji
t
t
Y
Y
.
FED System Rezerwy Finansowej Stanów Zjednoczonych różni się swoim podejściem
od EBC, ponieważ oprócz zapobiegania nadmiernemu wzrostowi cen jego działania
ukierunkowane są również na pobudzanie gospodarki (cel krótkoterminowy).
Dezinflacja – czyli świadomie realizowana polityka polegająca na redukowaniu stopy
inflacji, Polityka ta – zgodnie z wcześniej prezentowaną regułą Taylora (funkcją reakcji banku
centralnego) - może mied jednak w okresie średnim swoje skutki w postaci wzrostu stopy
bezrobocia. Odwrotną zależnośd pomiędzy stopą bezrobocia a stopą inflacji pokazuje nam
równanie krzywej Philipsa:
Gdzie:
– stopa inflacji w okresie t
– stopa inflacji w okresie t-1
-
Współczynnik α określa wrażliwośd zmiany stopy inflacji w czasie w zależności od odchylenia
aktualnej stopy bezrobocia od jej poziomu naturalnego. Współczynnik α może byd różny dla różnych
krajów.
- stopa bezrobocia w okresie t
– stopa bezrobocia naturalnego
Z równania krzywej Philipsa wynika, że stopa bezrobocia naturalnego może byd definiowana
jako stopa bezrobocia nie powodująca zmian w inflacji, dosłownie nie przyspieszająca inflacji tzn.
NAIRU (Non-Accelerating Inflation Rate of Unemployment). A zatem gdy u
t
równa się u
n
wówczas Δπ
t
= 0.
Bank centralny zdając sobie sprawę z faktu, że podjęcie działao dezinflacyjnych będzie
prawdopodobnie skutkowało wzrostem bezrobocia stara się uwzględniad w swoich kalkulacjach
zarówno stratę z tytułu odchylenie od zamierzonego celu inflacyjnego, jak i stratę wynikającą z tytułu
wzrostu bezrobocia będącego efektem ubocznym walki z inflacją. Funkcja straty banku centralnego
ma postad:
Gdzie:
L
t
– strata banku centralnego lub inaczej mówiąc koszt alternatywny podjęcia decyzji w sprawie
polityki dezinflacyjnej
b – współczynnik określający poziom „dbałości” banku centralnego o wysokośd stopy bezrobocia
W zależności od wielkości współczynnika b banki centralne dzielimy na:
„mokre nosy” lub „gołębie” – tak nazywamy te banki centralne, które ustalają poziom
współczynnika b tak by b>0, co oznacza, że uwzględniają one stratę wynikającą ze wzrostu
stopy bezrobocia i starają się ją zminimalizowad.
„zadarte nosy” lub „jastrzębie” – tak nazywamy te banki centralne, które ustalają poziom
współczynnika b tak, że b=0, co oznacza, że są nastawiona głównie na prowadzenie działao
dezinfacyjnych i nie przejmują się skutkami w postaci wzrostu stopy bezrobocia.
Aby skutecznie zaprojektowad ścieżkę dezinflacyjną potrzebujemy jeszcze jednego równania -
równania Okuna:
Gdzie:
– współczynnik charakterystyczny dla danej gospodarki określający stopieo zależności wysokości
stóp bezrobocia od stopy wzrostu gospodarczego
- stopa wzrostu gospodarczego w okresie t
– naturalna stopa wzrostu gospodarczego
Tak aby uzyskad informację na temat pożądanego poziomu stopy wzrostu nominalnej podaży
pieniądza niezbędnego do wdrożenia w praktyce planu dezinflacyjnego wródmy na chwilę do
równania opisującego krzywą AD. Wiemy z niego, że dochód jest dodatnią funkcją realnej podaży
pieniądza:
Gdzie:
A – jest współczynnikiem charakteryzującym daną gospodarkę, dla uproszczenia dalszej
analizy zakładamy, że A jest równe 1.
Mamy więc równanie:
Zlogarytmowanie obu stron równania pozwala nam uzyskad następującą postad równania:
Równanie to pokazuje nam, że stopa wzrostu dochodu zależy od stopy wzrostu
nominalnej podaży pieniądza pomniejszonej o stopę wzrost ogólnego poziomu cen (de facto
stopę inflacji). Zamieniając w powyższym równaniu oznaczenia na stosowane dotychczas
otrzymujemy zatem postad:
Otrzymaliśmy więc trzy równania:
1. Równanie krzywej Philipsa:
2. Równanie Okuna:
3. Oraz ostatnie równanie:
Znając te równania, oraz wartości współczynników alfa i beta możemy zaprojektowad
ścieżkę dezinflacyjną dla danej gospodarki.
Przykład
Załóżmy, że bank centralny kraju A realizuje politykę celu inflacyjnego polegającą na zbiciu
inflacji z poziomu 14% do 4% przez pięd lat przy założeniu stałej stopy spadku. Zaprojektuj
ścieżkę deziflacyjną wiedząc, że:
α = 1
β = 0,3
= 3%
U
n
= 4%
T
0
T
1
T
2
T
3
T
4
T
5
π
14%
12%
10%
8%
6%
4%
u
4%
6%
6%
6%
6%
6%
g
Y
3%
-3,67%
3%
3%
3%
3%
g
M
17%
8,33%
13%
11%
9%
7%
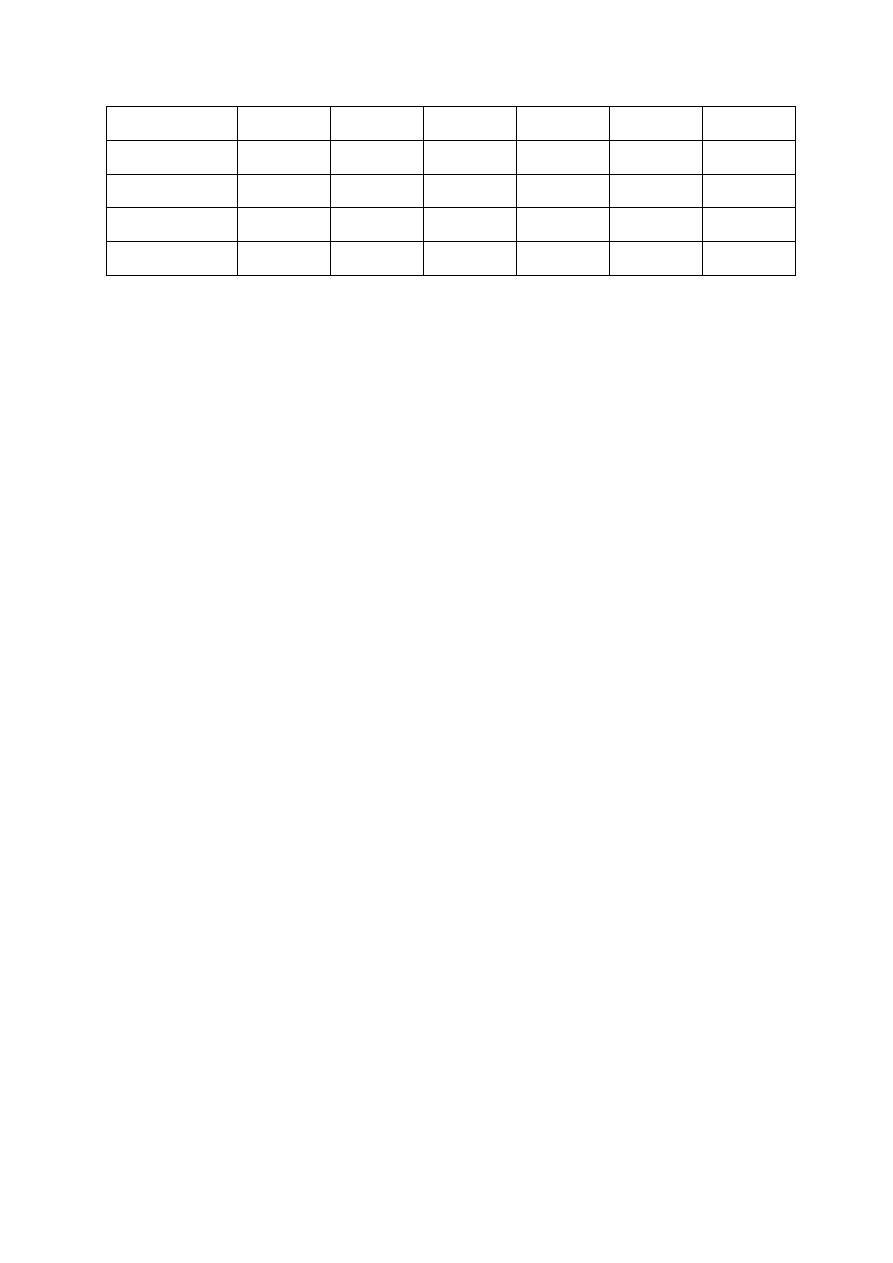
W pierwszym wierszu wpisujemy cel inflacyjny jaki założył bank centralny. Zaczynamy
od wyjściowej stopy inflacji wynoszącej 14% i dla kolejnych okresów od t
1
do t
5
wpisujemy
zakładane spadki inflacji tak by w ostatnim okresie osiągnąd zamierzoną wartośd. Przyjęcie
założeo o zrównoważonej polityce celu inflacyjnego oznacza, że spadki stopy inflacji w
każdym z okresów funkcjonowania programu będą takie same. Przyjmując takie wytyczne
wypełniamy pierwszy wiersz tabeli rozpoczynając projektowanie ścieżki dezinflacyjnej od
wyjściowego poziomu 14%. Pozostałe wyjściowe dane odpowiadają wielkościom zmiennych
makroekonomicznych w równowadze tj. naturalnej stopie bezrobocia i normalnej stopie
wzrostu gospodarczego. Początkową stopę wzrostu nominalnej podaży pieniądza
otrzymujemy dodając do siebie (zgodnie z trzecim równaniem) stopę wzrostu i stopę inflacji.
Zaczynamy od obliczenia (z pierwszego równania) wysokości stopy bezrobocia dla kolejnych
okresów:
1.
U
t1
= 6%
2.
u
t2
= 6%
3. Itd.
Dla pozostałych okresów wysokośd stopy bezrobocia nie zmieni się ponieważ
spadki inflacji są identyczne dla wszystkich tych okresów.
Aby osiągnąd zamierzony cel dezinflacyjny, czyli w każdym roku obniżad inflację o 2 punkty
procentowe, należy więc zaakceptowad odchylenie stopy bezrobocia także powyżej dwóch
punktów od jej naturalnego poziomu.
Następnie obliczamy (z drugiego równania) wzrosty dochodu dla kolejnych okresów:
1.
03
,
0
3
,
0
04
,
0
06
,
0
t
Y
g
%
67
,
3
t
Y
g
2.
03
,
0
3
,
0
06
,
0
06
,
0
t
Y
g
%
3
t
Y
g
Dla pozostałych okresów stopa wzrostu gospodarczego będzie równa normalnej
stopie wzrostu, ponieważ poczynając od okresu 2 stopa bezrobocia nie zmieni się.
W pierwszym roku realizacji polityki dezinflacyjnej stopa wzrostu PKB będzie musiała
zmniejszyd się o ponad 6 punktów procentowych i będzie ujemna. Polityka dezinflacyjna
spowodowała więc spadek PKB. W kolejnych latach stopa bezrobocia nie zmienia się, a stopa
wzrostu PKB będzie równa normalnej stopie wzrostu.
Ostatni etap stanowi obliczenie stopy nominalnej podaży pieniądza dla każdego z okresów.
Otrzymujemy ją wykorzystując równanie 3, dla każdego z okresów sumując stopę inflacji i
stopę wzrostu gospodarczego. Bank centralny dostosowując podaż pieniądza do
zaprojektowanych dla kolejnych lat poziomów będzie realizował politykę dezinflacyjną.