1. Elementy logiki

Zakres podstawowy

Praca klasowa nr 1 gr. A

(Kod: K1_D1_P_K1A)

Zadanie 1. (3 p.)
Oceń wartości logiczne zdań:
a) Trójkąt, którego boki mają długości 6, 8, 10 jest prostokątny.
b) Dla dowolnej liczby x prawdziwa jest równość: (x – 4)

2

= x

2

+ 16.

c) Istnieje wielokąt, którego liczba przekątnych jest równa liczbie jego boków.

Zadanie 2. (4 p.)
Uczeń przystąpił do egzaminu składającego się z dwóch części. Z każdej części mógł uzyskać
maksymalnie po 15 punktów. Warunkiem zdania egzaminu było uzyskanie z każdej części co
najmniej po 7 punktów i z obu części w sumie więcej niż 15 punktów. Czy z całą pewnością
możemy stwierdzić, który z chłopców zdał egzamin, a któremu się nie powiodło jeśli:
a) Wacek uzyskał w sumie z obu części 60% możliwych punktów.
b) Piotr otrzymał z jednej części 10 punktów, a w sumie uzyskał 16 punktów.
Odpowiedź uzasadnij.

Zadanie 3. (4 p.)
Oceń wartości logiczne zdań:

p: – 2

4

= 16, q:

2

2

4

3 +

= 7, r: 2 jest liczb

ą

pierwsz

ą

,

a nast

ę

pnie oce

ń

warto

ść

logiczn

ą

zdania:

(

p

⇒

q

)

∧

r.

Zadanie 4. (3 p.)
Poni

ż

ej podane s

ą

twierdzenia. Oce

ń

ich warto

ś

ci logiczne.

a) Je

ś

li liczba jest podzielna przez 3, to jest podzielna przez 6.

b) Je

ś

li przek

ą

tne czworok

ą

ta przecinaj

ą

si

ę

pod k

ą

tem prostym, to ten czworok

ą

t jest

rombem.
c) Je

ś

li trójk

ą

t ma wszystkie k

ą

ty ostre, to jest ostrok

ą

tny.

Zadanie 5. (3 p.)
Podaj prawo negacji alternatywy i udowodnij je. Napisz negacj

ę

zdania:

Pojadę w góry lub

nie pojadę nad morze

.

Zadanie 6. (3 p.)
Oznaczmy zdania: p –

Mój ojciec ma nowe renault clio

.

q –

Moja mama nie ma prawa jazdy

.

r –

Ojciec podwozi mamę do pracy

.

Zapisz zdanie: (p

∧

q)

⇒

r. Podaj zaprzeczenie utworzonego zdania, korzystaj

ą

c z prawa

negacji implikacji:

¬(

p

⇒

q

)

⇔

[p

∧

(

¬

q

)

].

Zadanie 7.***
Prawdziwe jest zdanie:

Jeśli Tomek jest gimnazjalistą, to Jacek jest licealistą i nieprawda, że

jeśli Wojtek studiuje prawo, to Tomek nie jest gimnazjalistą.

Czy prawd

ą

jest,

ż

e Tomek jest

gimnazjalist

ą

, Jacek licealist

ą

, a Wojtek studentem prawa?

Odpowiedzi

(Kod: K1_D1_P_K1A)

1. Zdania prawdziwe – a, c; zdanie fałszywe – b.
2. Nie wiadomo czy Wacek zdał egzamin, czy nie zdał egzaminu; Piotr nie zdał.
3. w(p) = 0, w(q) = 0, w(r) = 1, w[

(

p

⇒

q

)

∧

r] = 1.

4. Twierdzenia fałszywe – a, b; twierdzenie prawdziwe – c.
5.

Nie pojadę w góry i pojadę nad morze

.

6. Zdanie brzmi:

Jeśli mój ojciec ma nowe renault clio i moja mama nie ma prawa jazdy to

ojciec podwozi mamę do pracy

. Zdanie po negacji:

Mój ojciec ma nowe renault clio i moja

mama nie ma prawa jazdy i ojciec nie podwozi mamy do pracy

.

7. Tak.

1. Elementy logiki

Zakres podstawowy

Praca klasowa nr 1 gr. B

(Kod: K1_D1_P_K1B)

Zadanie 1. (3 p.)
Oce

ń

warto

ś

ci logiczne zda

ń

:

a) Trójk

ą

t, którego boki maj

ą

długo

ś

ci 5, 12, 13 jest prostok

ą

tny.

b) Dla dowolnej liczby x prawdziwa jest równo

ść

: (x + 3)

2

= x

2

+ 3x + 9.

c) Istnieje trójk

ą

t, który ma dwa k

ą

ty rozwarte.

Zadanie 2. (4 p.)
Ucze

ń

przyst

ą

pił do egzaminu składaj

ą

cego si

ę

z dwóch cz

ęś

ci. Z ka

ż

dej cz

ęś

ci mógł uzyska

ć

maksymalnie po 15 punktów. Warunkiem zdania egzaminu było uzyskanie z ka

ż

dej cz

ęś

ci co

najmniej po 7 punktów i z obu cz

ęś

ci w sumie wi

ę

cej ni

ż

15 punktów. Czy z cał

ą

pewno

ś

ci

ą

mo

ż

emy stwierdzi

ć

, który z chłopców zdał egzamin, a któremu si

ę

nie powiodło je

ś

li:

a) Marcin uzyskał w sumie z obu cz

ęś

ci 16 punktów.

b) Piotr otrzymał z jednej cz

ęś

ci 8 punktów, a w sumie uzyskał 45% punktów.

Odpowied

ź

uzasadnij.

Zadanie 3. (4 p.)
Oce

ń

warto

ś

ci logiczne zda

ń

:

p: – 3

2

= – 9, q:

49

25

+

= 12, r: 3 jest liczb

ą

pierwsz

ą

,

a nast

ę

pnie oce

ń

warto

ść

logiczn

ą

zdania:

(

p

⇒

q

)

∧

r.

Zadanie 4. (3 p.)
Poni

ż

ej podane s

ą

twierdzenia. Oce

ń

ich warto

ś

ci logiczne.

a) Je

ś

li liczba jest podzielna przez 4, to jest podzielna przez 2.

b) Je

ś

li przek

ą

tne czworok

ą

ta przecinaj

ą

si

ę

pod k

ą

tem prostym, to ten czworok

ą

t jest

kwadratem.
c) Je

ś

li trójk

ą

t ma dwa k

ą

ty ostre, to jest ostrok

ą

tny.

Zadanie 5. (3 p.)
Podaj prawo negacji koniunkcji i udowodnij je. Napisz negacj

ę

zdania:

Nie kupię pomidorów

i kupię mandarynki

.

Zadanie 6. (3 p.)
Oznaczmy zdania: p –

Pan Kowalski kupił kwiaty

.

q –

Mężczyzna wybrał róże

.

r –

Róże są herbaciane

.

Zapisz zdanie: (p

∧

q)

⇒

r. Podaj zaprzeczenie utworzonego zdania, korzystaj

ą

c z prawa

negacji implikacji:

¬(

p

⇒

q

)

⇔

[p

∧

(

¬

q

)

].

Zadanie 7.***
Prawdziwe jest zdanie:

Jeśli Ania dostała piątkę z klasówki, to Beata dostała trójkę i

nieprawdą jest, że Ania dostała piątkę i Beata trójkę.

Czy Ania dostała pi

ą

tk

ę

z klasówki?

Odpowiedzi

(Kod: K1_D1_P_K1B)

1. Zdanie prawdziwe – a; zdania fałszywe – b, c.
2. Nie wiadomo czy Marcin zdał, czy nie zdał egzaminu; Piotr nie zdał.
3. w(p) = 1, w(q) = 0, w(r) = 1, w[

(

p

⇒

q

)

∧

r] = 0.

4. Twierdzenie prawdziwe – a, twierdzenia fałszywe – b, c.
5.

Kupię pomidory lub nie kupię mandarynek

.

6. Zdanie brzmi:

Jeśli pan Kowalski kupił kwiaty i mężczyzna wybrał róże, to róże są

herbaciane

. Zdanie po negacji:

Pan Kowalski kupił kwiaty i mężczyzna wybrał róże i róże nie

są herbaciane

.

7. Nie.

1. Elementy logiki

Zakres podstawowy

Praca klasowa nr 2 gr. A

(Kod: K1_D1_P_K2A)

Zadanie 1. (3 p.)
Które z poni

ż

szych wypowiedzi s

ą

zdaniami logicznymi prawdziwymi?

a) x + 1 = 3.

c) Czy masz dobry humor?

b) 1 < 3.

d) Kwadrat dowolnej liczby rzeczywistej jest dodatni.

Zadanie 2. (3 p.)
Dane jest twierdzenie:

Jeśli liczba naturalna jest podzielna przez 2 i przez 3, to jest podzielna

przez 6.

a) Czy podane twierdzenie jest prawdziwe?
b) Sformułuj twierdzenie odwrotne do danego.
c) Oce

ń

warto

ść

logiczn

ą

twierdzenia odwrotnego do danego.

Zadanie 3. (3 p.)

Wiadomo,

ż

e w(p

⇒

q) = 0. Jak

ą

warto

ść

logiczn

ą

ma zdanie: [p

∧

(

¬

q

)

]

⇔

q ?

Zadanie 4. (3 p.)
Dane s

ą

zdania:

p:

2 jest liczb

ą

wymiern

ą

, q: 3 jest wi

ę

ksze od 8.

a) Napisz alternatyw

ę

powy

ż

szych zda

ń

u

ż

ywaj

ą

c symboli matematycznych, a nast

ę

pnie

podaj zaprzeczenie utworzonego zdania.
b) Oce

ń

warto

ść

logiczn

ą

alternatywy zda

ń

.

Zadanie 5. (4 p.)
Uzupełnij tabelk

ę

i oce

ń

, czy wyra

ż

enie rachunku zda

ń

: (

¬

p

∧

q

)

⇒

(

p

⇔

q

)

jest prawem

logicznym.

p

q

¬

p

¬

p

∧

q

p

⇔

q

(

¬

p

∧

q

)

⇒

(

p

⇔

q

)

1

1

0

0

1

1

0

0

1

0

0

1

Zadanie 6. (4 p.)
Oce

ń

warto

ść

logiczn

ą

zdania:

Dowolna liczba rzeczywista dodatnia jest nie mniejsza od

odwrotności tej liczby

i zapisz je, u

ż

ywaj

ą

c kwantyfikatorów i symboli matematycznych.

Podaj jego negacj

ę

.

Zadanie 7.***
Prawdziwe jest zdanie:

Nieprawda, że jeśli Platon założył Akademię, to jeśli Arystoteles był

uczniem Platona, to Arystoteles nie uczęszczał do Akademii.

Czy na podstawie tej informacji mo

ż

na udzieli

ć

odpowiedzi na pytanie:

Czy Platon założył

Akademię?

Je

ś

li tak, to podaj i uzasadnij t

ę

odpowied

ź

.

Odpowiedzi

(Kod: K1_D1_P_K2A)

1. Tylko b) jest zdaniem prawdziwym.
2. a) Tak;
b) Je

ś

li liczba jest podzielna przez 6 to jest podzielna przez 2 i przez 3;

c) Twierdzenie jest prawdziwe.
3. Zdanie jest prawdziwe.
4. a)

8

3

W

2

>

∨

∈

;

8

3

W

2

≤

∧

∉

;

b) Zdanie jest fałszywe.
5. Wyra

ż

enie rachunku zda

ń

nie jest tautologi

ą

.

6.

a

1

a

:

R

a

≥

∈

∀

+

; zdanie po negacji:

a

1

a

:

R

a

<

∈

∃

+

.

7. Tak.

1. Elementy logiki

Zakres podstawowy

Praca klasowa nr 2 gr. B

(Kod: K1_D1_P_K2B)

Zadanie 1. (3 p.)
Które z poni

ż

szych wypowiedzi s

ą

zdaniami logicznymi fałszywymi?

a) 4 jest liczb

ą

nieparzyst

ą

.

c) x + 1 < 6

b) π ma warto

ść

równ

ą

3,14.

d) Kwadrat dowolnej liczby rzeczywistej jest nieujemny.

Zadanie 2. (3 p.)
Dane jest twierdzenie:

Jeśli liczba naturalna jest podzielna przez 15, to jest podzielna

przez 3.

a) Czy podane twierdzenie jest prawdziwe?
b) Sformułuj twierdzenie odwrotne do danego.
c) Oce

ń

warto

ść

logiczn

ą

twierdzenia odwrotnego do danego.

Zadanie 3. (3 p.)
Wiadomo,

ż

e w(p ∨ q) = 0. Jak

ą

warto

ść

logiczn

ą

ma zdanie: (¬p ∧ q )

⇒

p?

Zadanie 4. (3 p.)
Dane s

ą

zdania:

p: 3 jest liczb

ą

niewymiern

ą

, q: 4 = –2.

a) Napisz koniunkcj

ę

powy

ż

szych zda

ń

u

ż

ywaj

ą

c symboli matematycznych, a nast

ę

pnie podaj

zaprzeczenie utworzonego zdania.
b) Oce

ń

warto

ść

logiczn

ą

koniunkcji zda

ń

.

Zadanie 5. (4 p.)
Uzupełnij tabelk

ę

i oce

ń

, czy wyra

ż

enie rachunku zda

ń

: [(p

⇒

q) ∨ (¬q)] ⇔ p jest prawem

logicznym.

p

q

p

⇒

q

¬q

(p

⇒

q) ∨ (¬q)

[(p

⇒

q) ∨ (¬q)] ⇔ p

1

0

0

1

1

1

0

0

0

1

1

1

Zadanie 6. (4 p.)
Oce

ń

warto

ść

logiczn

ą

zdania:

Dla każdej liczby rzeczywistej x suma liczby x i jej kwadratu

jest dodatnia

i zapisz je, u

ż

ywaj

ą

c kwantyfikatorów i symboli matematycznych. Podaj jego

negacj

ę

.

Zadanie 7.***
Prawdziwe jest zdanie:

Nieprawda, że jeśli Platon założył Akademię, to jeśli Arystoteles był

uczniem Platona, to Arystoteles nie uczęszczał do Akademii.

Czy na podstawie tej informacji mo

ż

na udzieli

ć

odpowiedzi na pytanie:

Czy Arystoteles był

uczniem Platona?

Je

ś

li tak, to podaj i uzasadnij t

ę

odpowied

ź

.

Odpowiedzi

(Kod: K1_D1_P_K2B)

1. Zdania logiczne fałszywe – a, b.
2. a) Twierdzenie jest prawdziwe;
b) Je

ś

li liczba jest podzielna przez 3 to jest podzielna przez 15;

c) Twierdzenie jest fałszywe.
3. Zdanie prawdziwe.
4. a)

2

4

NW

3

−

=

∧

∈

;

2

4

NW

3

−

≠

∨

∉

;

b) Zdanie fałszywe.
5. Nie jest prawem logicznym.
6.

0

x

x

:

R

x

2

>

+

∈

∀

; zdanie po negacji

0

x

x

:

R

x

2

≤

+

∈

∃

.

7. Tak

1. Elementy logiki

Zakres rozszerzony

Praca klasowa nr 1 gr. A

(Kod: K1_D1_R_K1A)

Zadanie 1. (5 p.)
Okre

ś

l, które z poni

ż

szych wyra

ż

e

ń

jest zdaniem, a które form

ą

zdaniow

ą

. Poni

ż

sze

wypowiedzi zapisz za pomoc

ą

kwantyfikatorów oraz symboli matematycznych. Oce

ń

warto

ś

ci logiczne zda

ń

.

a) Odwrotno

ść

liczby a jest równa 5 lub a jest liczb

ą

podzieln

ą

przez 7.

b) Istnieje liczba rzeczywista p, której warto

ść

bezwzgl

ę

dna jest liczb

ą

niedodatni

ą

.

c) Pierwiastek kwadratowy z kwadratu dowolnej liczby rzeczywistej b jest równy tej liczbie.

Zadanie 2. (5 p.)
a) Podaj prawo negacji implikacji dwóch zda

ń

.

b) Udowodnij prawo negacji implikacji dwóch zda

ń

.

c) Podaj zaprzeczenie zdania:

Jeśli będę otrzymywał dobre stopnie w liceum to dostanę się na

studia lub wyjadę na stypendium za granicę.

Zadanie 3. (2 p.)
Wiadomo,

ż

e w(p

∧

q) = 1. Jak

ą

warto

ść

logiczn

ą

ma zdanie: [(¬p ⇔ q) ∧ (p ∨ q)]

⇒

q?

Zadanie 4. (5 p.)
W

ś

ród poni

ż

szych twierdze

ń

znajduj

ą

si

ę

twierdzenia prawdziwe oraz fałszywe.

Wybierz twierdzenia fałszywe. Utwórz twierdzenia odwrotne do nich i oce

ń

ich warto

ść

logiczn

ą

.

a) Je

ś

li liczba jest parzysta, to jest podzielna przez 12.

b) Je

ś

li przek

ą

tne czworok

ą

ta przecinaj

ą

si

ę

pod k

ą

tem prostym, to ten czworok

ą

t jest

kwadratem.
c) Je

ś

li trójk

ą

t jest ostrok

ą

tny, to ma wszystkie k

ą

ty ostre.

Zadanie 5. (3 p.)
Wyznacz dziedzin

ę

formy zdaniowej:

3

x

2 − = 5 ∧ x

2

– 8x + 16 = 0. Podaj zbiór

wszystkich elementów, które spełniaj

ą

t

ę

form

ę

zdaniow

ą

.

Zadanie 6.***
Napisz negacj

ę

zdania:

Trawa jest zielona wtedy i tylko wtedy gdy świeci słońce

.

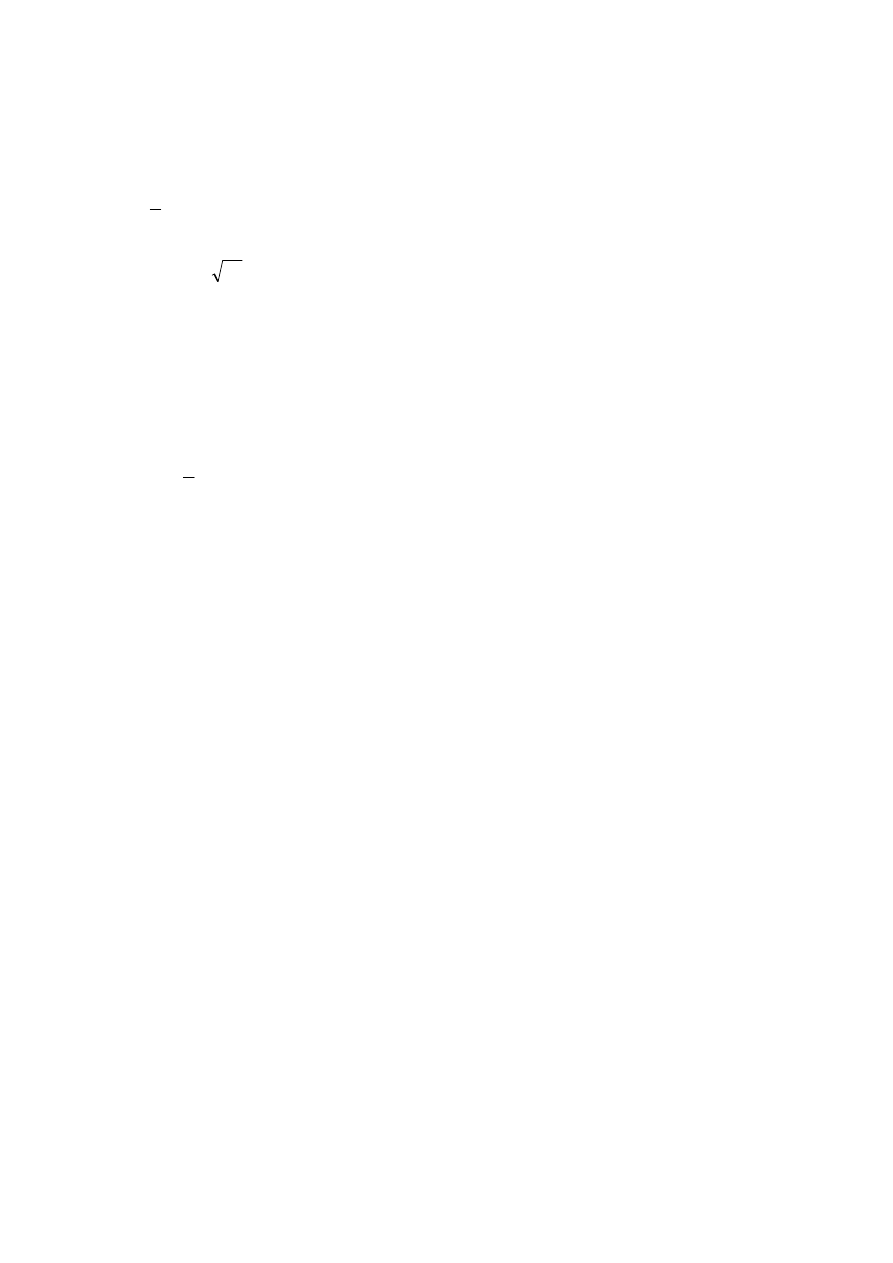
Odpowiedzi

(Kod: K1_D1_R_K1A)

1. a)

a

|

7

5

a

1

∨

=

;

b)

0

|

p

:|

r

p

≤

∈

∃

( zdanie prawdziwe);

c)

b

b

:

R

b

2

=

∈

∀

(zdanie fałszywe).

2. a) [¬(p

⇒

q)] ⇔ [p ∧ (¬q)];

c)

Będę otrzymywał dobre stopnie w liceum i nie dostanę się na studia i nie wyjadę na

stypendium za granicę

.

3. Zdanie jest prawdziwe.
4. Twierdzenia fałszywe – a, b;
a) Je

ś

li liczba jest podzielna przez 12, to jest parzysta (twierdzenie prawdziwe).

b) Je

ś

li czworok

ą

t jest kwadratem, to jego przek

ą

tne przecinaj

ą

si

ę

pod k

ą

tem prostym

(twierdzenie prawdziwe).

5. D =

〈

1

2

1

, +∞) ; x ∈ {4}.

6.

Trawa jest zielona i nie świeci słońce lub świeci słońce i trawa nie jest zielona

.

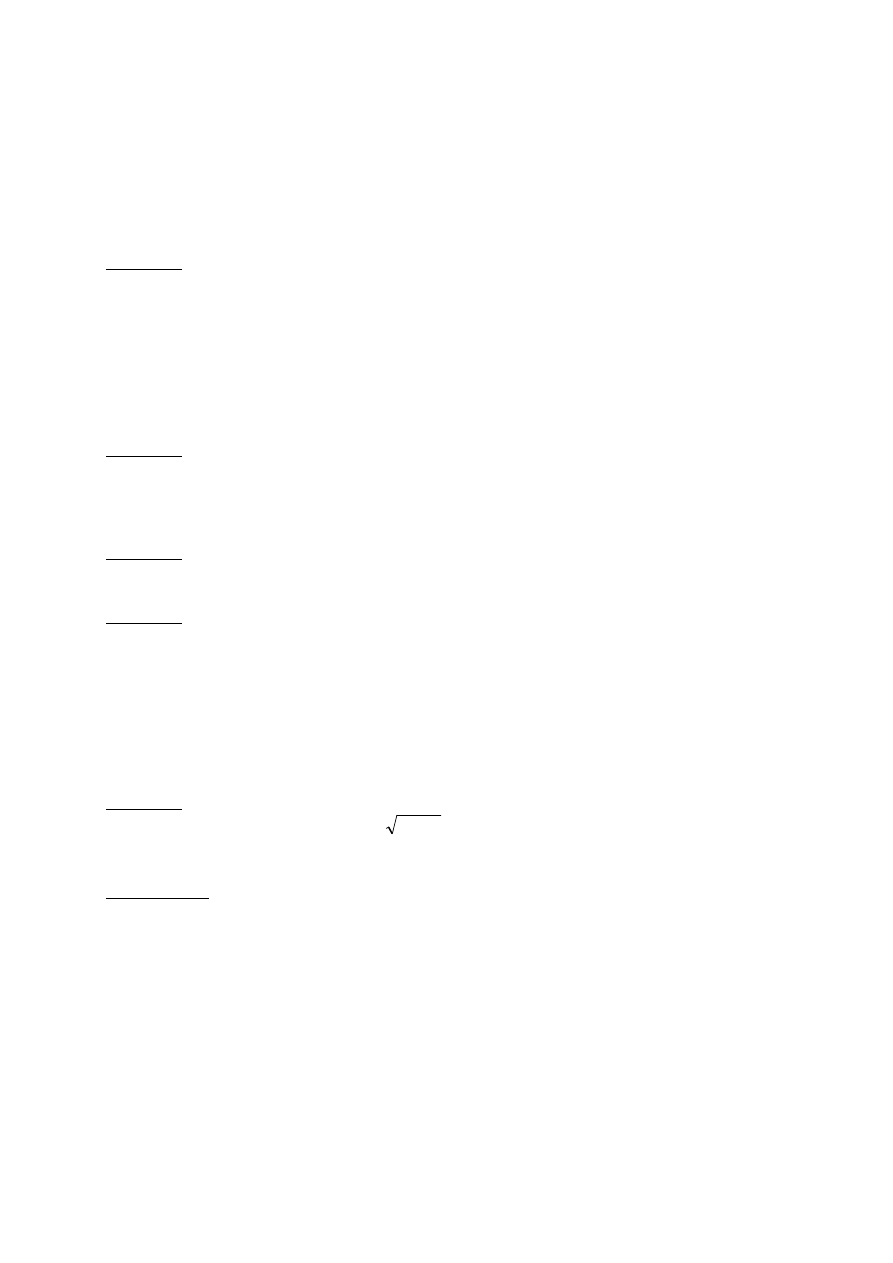
1. Elementy logiki

Zakres rozszerzony

Praca klasowa nr 1 gr. B

(Kod: K1_D1_R_K1B)

Zadanie 1. (5 p.)
Okre

ś

l, które z poni

ż

szych wyra

ż

e

ń

jest zdaniem, a które form

ą

zdaniow

ą

. Poni

ż

sze

wypowiedzi zapisz za pomoc

ą

kwantyfikatorów oraz symboli matematycznych. Oce

ń

warto

ś

ci logiczne zda

ń

.

a) Liczba przeciwna do liczby a jest równa 5 lub a jest liczb

ą

podzieln

ą

przez 3.

b) Istnieje liczba rzeczywista r, której kwadrat jest liczb

ą

niedodatni

ą

.

c) Pierwiastek kwadratowy z kwadratu dowolnej liczby rzeczywistej y jest równy warto

ś

ci

bezwzgl

ę

dnej tej liczby.

Zadanie 2. (5 p.)
a) Podaj prawo alternatywy dwóch zda

ń

.

b) Udowodnij prawo alternatywy dwóch zda

ń

.

c) Podaj zaprzeczenie zdania:

Jem dużo cukierków lub jeśli jest gorąco, to nie gardzę lodami

.

Zadanie 3. (2 p.)
Wiadomo,

ż

e w(p

⇒

q) = 0. Jak

ą

warto

ść

logiczn

ą

ma zdanie: [(¬p ⇔ q) ∧ (p ∨ q)]

⇒

q?

Zadanie 4. (5 p.)
W

ś

ród poni

ż

szych twierdze

ń

znajduj

ą

si

ę

twierdzenia prawdziwe oraz fałszywe.

Wybierz twierdzenia fałszywe. Utwórz twierdzenia odwrotne do nich i oce

ń

ich warto

ść

logiczn

ą

.

a) Je

ś

li liczba jest nieparzysta, to jest podzielna przez 3.

c) Je

ś

li przek

ą

tne czworok

ą

ta przecinaj

ą

si

ę

pod k

ą

tem prostym, to ten czworok

ą

t jest

deltoidem.
c) Je

ś

li trójk

ą

t jest rozwartok

ą

tny, to ma jeden k

ą

t rozwarty.

Zadanie 5. (3 p.)
Wyznacz dziedzin

ę

formy zdaniowej:

5

x

3 − = 2 ∧ x

2

– 9 = 0. Podaj zbiór wszystkich

elementów, które spełniaj

ą

t

ę

form

ę

zdaniow

ą

.

Zadanie 6.***
Napisz negacj

ę

zdania:

Jest smutno wtedy i tylko wtedy, gdy pada deszcz

.

Odpowiedzi

(Kod: K1_D1_R_K1B)

1. a) – a = 5 ∨ 3|a;
b)

0

r

:

R

r

2

≤

∈

∃

(zdanie prawdziwe);

c)

|

y

|

y

:

R

y

2

=

∈

∀

(zdanie prawdziwe).

2. a) [¬(p ∨ q)] ⇔ [(¬p) ∧ (¬q)];
c)

Nie jem dużo cukierków i jest gorąco i gardzę lodami

.

3. Zdanie jest fałszywe.
4. Twierdzenia fałszywe – a, b.
Twierdzenia odwrotne:

a) Je

ś

li liczba jest podzielna przez 3, to jest nieparzysta (twierdzenie fałszywe).

b) Je

ś

li czworok

ą

t jest deltoidem, to jego przek

ą

tne przecinaj

ą

si

ę

pod k

ą

tem prostym

(twierdzenie prawdziwe).

5. D =

)

,

3

2

1 +∞

, x ∈ {3}

6.

Jest smutno i nie pada deszcz lub pada deszcz i nie jest smutno

.

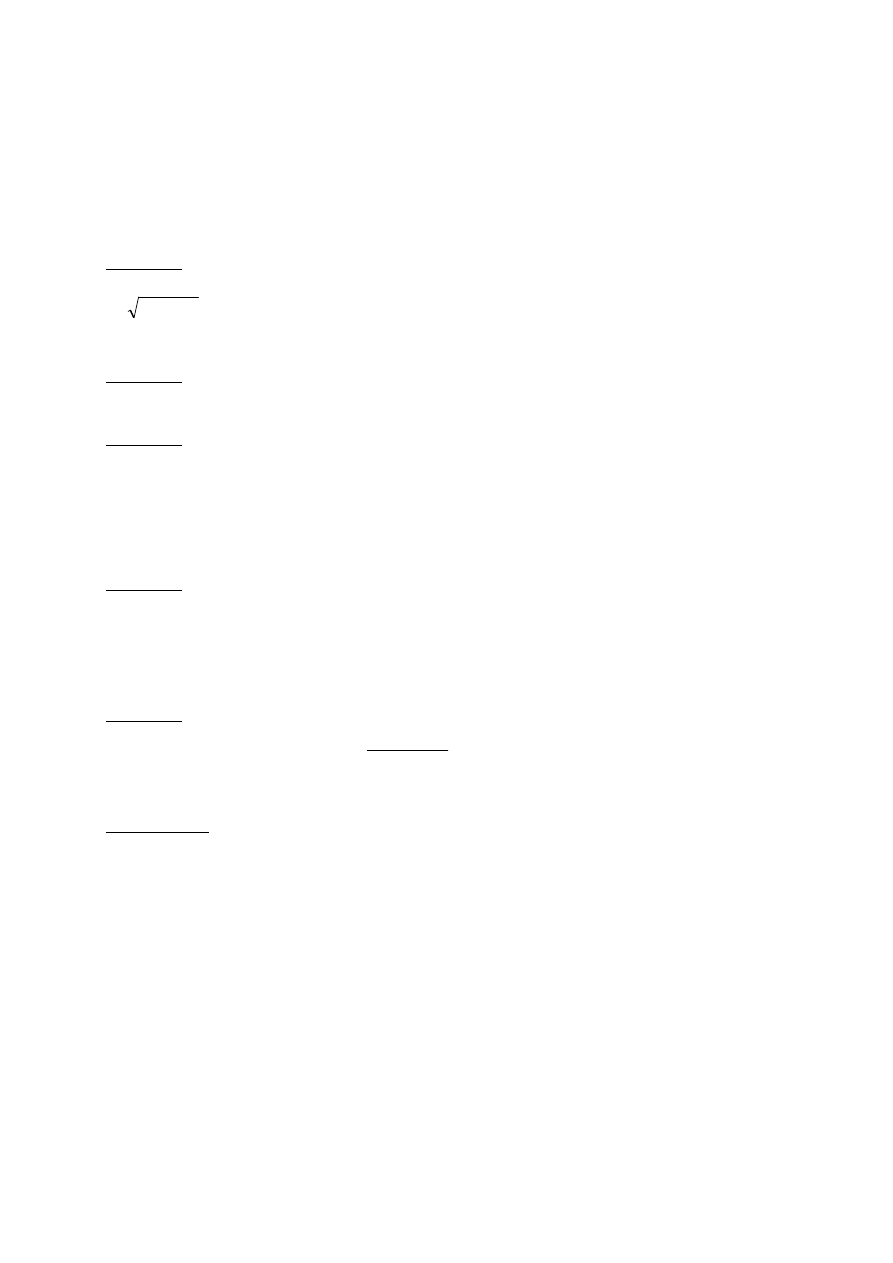
1. Elementy logiki

Zakres rozszerzony

Praca klasowa nr 2 gr. A

(Kod: K1_D1_R_K2A)

Zadanie 1. (5 p.)
Oce

ń

warto

ś

ci logiczne zda

ń

(podaj równie

ż

warto

ś

ci logiczne zda

ń

składowych):

a)

19

7

12

2

2

=

+

∨ 4

10

+ 4

10

+ 4

10

+ 4

10

= 4

40

.

b) Istnieje liczba pierwsza mniejsza od liczby 2.

Zadanie 2. (3 p.)
Sprawd

ź

, czy podane wyra

ż

enie rachunku zda

ń

[¬(¬p ∨ ¬q)] ⇔ (p ∧ q) jest tautologi

ą

.

Zadanie 3. (4 p.)
Zapisz za pomoc

ą

kwantyfikatorów i symboli matematycznych nast

ę

puj

ą

ce zdania. Oce

ń

ich

warto

ś

ci logiczne.

a) Istnieje taka liczba rzeczywista p, której sze

ś

cian jest wi

ę

kszy od jej podwojonego

kwadratu.
b) Dowolna liczba rzeczywista x jest równa swojej odwrotno

ś

ci.

Zadanie 4. (5 p.)
Napisz zaprzeczenia poni

ż

szych zda

ń

:

a)

Kochanowski napisał „Treny” lub Mickiewicz jest autorem „Dziadów”

.

b)

Jeśli koło jest figurą ograniczoną, to równoległobok jest trapezem

.

c)

]

1

x

0

2

x

[

:

R

x

2

≤

∧

>

−

∈

∀

.

Zadanie 5. (3 p.)

Okre

ś

l dziedzin

ę

formy zdaniowej:

0

4

x

4

x

x

2

x

2

2

=

+

−

−

. Podaj zbiór wszystkich elementów

spełniaj

ą

cych t

ę

form

ę

zdaniow

ą

.

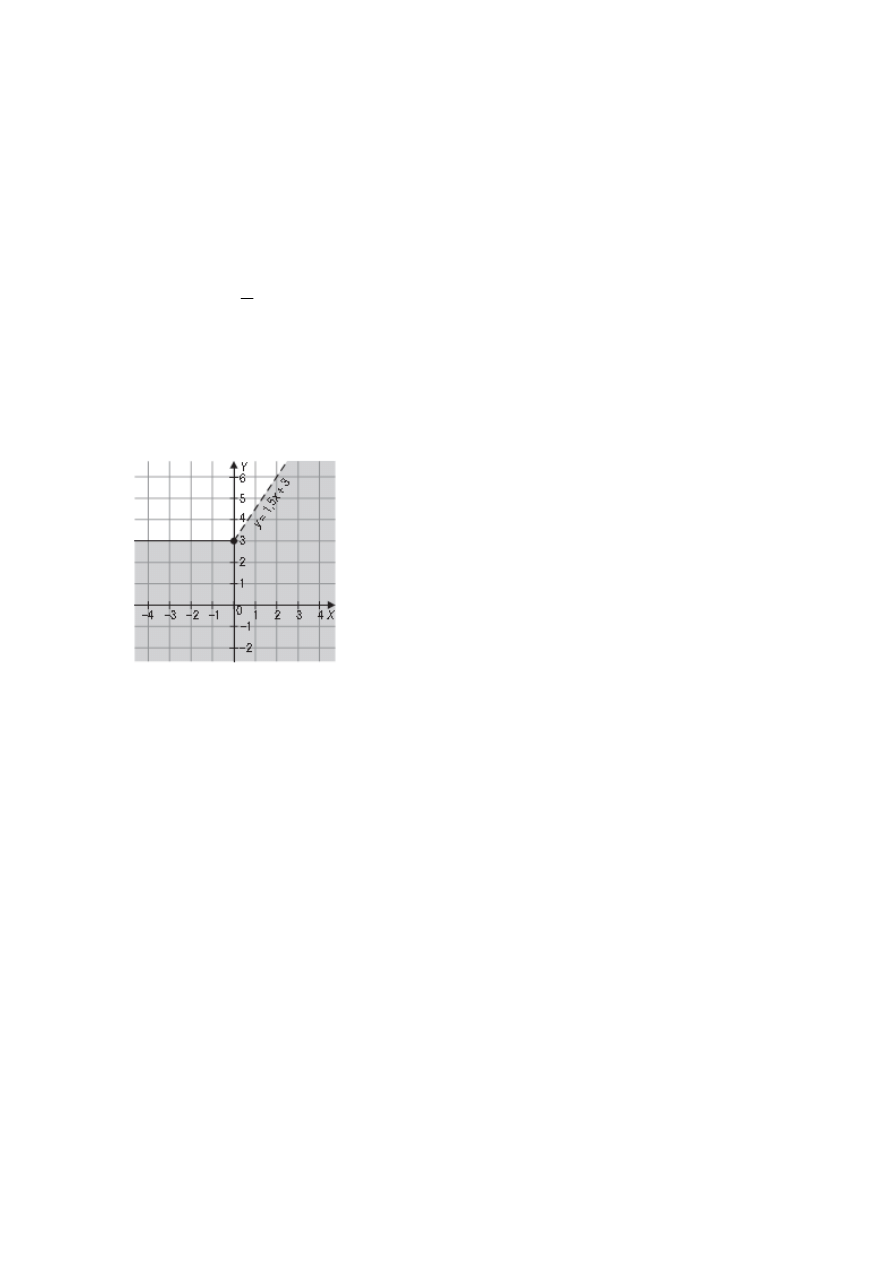
Zadanie 6.***
Na płaszczy

ź

nie z prostok

ą

tnym układem współrz

ę

dnych zaznacz zbiór wszystkich punktów,

których współrz

ę

dne spełniaj

ą

form

ę

zdaniow

ą

F(x, y): y > 3

⇒

2y – 3x < 6.

Odpowiedzi

(Kod: K1_D1_R_K2A)

1. a) Zdanie fałszywe,
b) zdanie fałszywe.
2. Wyra

ż

enie jest tautologi

ą

.

3. a)

2

3

p

2

p

:

R

p

>

∈

∃

;

b)

x

1

x

:

R

x

=

∈

∀

; a – zdanie prawdziwe; b – zdanie fałszywe.

4. a)

Kochanowski nie napisał „Trenów” i Mickiewicz nie jest autorem „Dziadów”.

b)

Koło jest figurą ograniczoną i równoległobok nie jest trapezem

.

c)

]

1

x

0

2

x

[

:

R

x

2

>

∨

≤

−

∈

∃

.

5. D = R – {2}, x ∈{0}.
6.

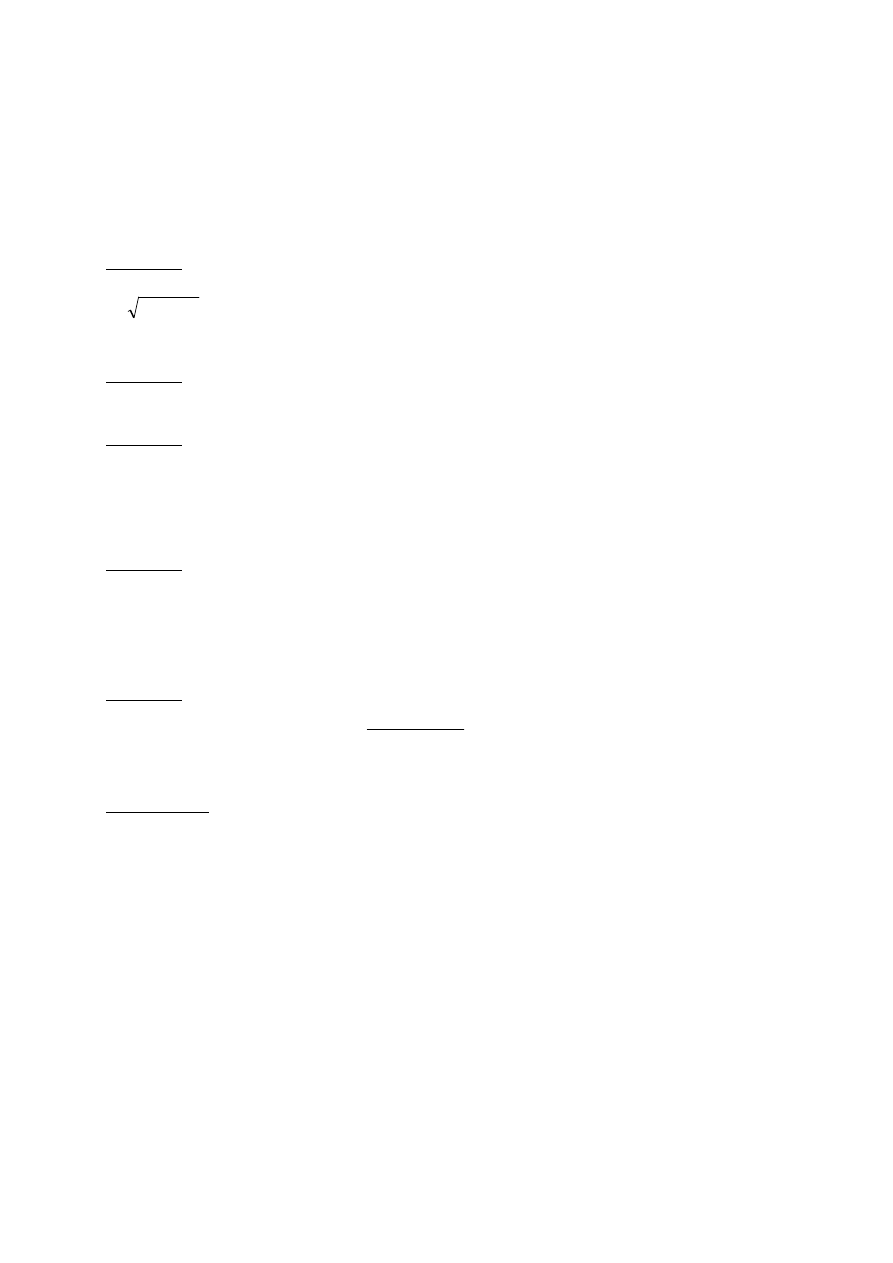
1. Elementy logiki

Zakres rozszerzony

Praca klasowa nr 2 gr. B

(Kod: K1_D1_R_K2B)

Zadanie 1. (5 p.)
Oce

ń

warto

ś

ci logiczne zda

ń

(podaj równie

ż

warto

ś

ci logiczne zda

ń

składowych):

a)

20

5

25

2

2

=

−

∧ 5

7

+ 5

7

+ 5

7

+ 5

7

+ 5

7

= 5

8

.

b) Istnieje liczba zło

ż

ona, która ma tylko dwa dzielniki naturalne.

Zadanie 2. (3 p.)
Sprawd

ź

, czy podane wyra

ż

enie rachunku zda

ń

: [(p ∨ ¬q)

⇒

p] ⇔ (¬p ∧ q) jest tautologi

ą

.

Zadanie 3. (4 p.)
Zapisz za pomoc

ą

kwantyfikatorów i symboli matematycznych nast

ę

puj

ą

ce zdania. Oce

ń

ich

warto

ść

logiczn

ą

.

a) Istnieje taka liczba rzeczywista a,

ż

e jej kwadrat jest mniejszy od potrojonej tej liczby.

b) Dowolna liczba rzeczywista k jest równa liczbie przeciwnej do jej sze

ś

cianu.

Zadanie 4. (5 p.)
Napisz zaprzeczenia poni

ż

szych zda

ń

:

a)

Kwadrat jest figurą osiowosymetryczną i prosta jest figurą środkowosymetryczną

.

b)

Jeśli wieloryb jest ssakiem, to płotka jest rybą

.

c)

]

1

x

x

x

[

:

R

x

3

≥

∨

>

∈

∃

.

Zadanie 5. (3 p.)

Okre

ś

l dziedzin

ę

formy zdaniowej:

25

x

10

x

x

5

x

2

2

+

+

+

= 0. Podaj zbiór wszystkich elementów

spełniaj

ą

cych t

ę

form

ę

.

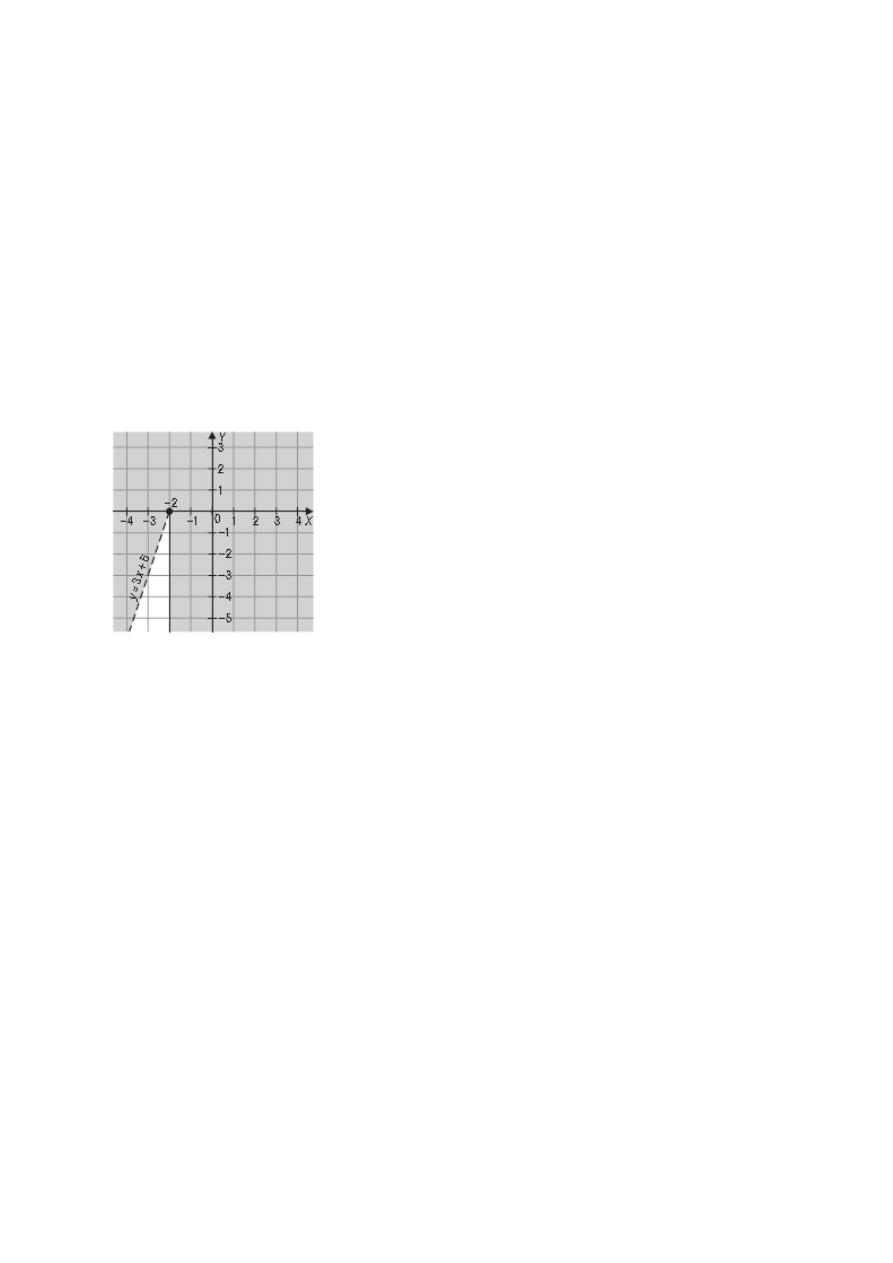
Zadanie 6.***
Na płaszczy

ź

nie z prostok

ą

tnym układem współrz

ę

dnych zaznacz zbiór wszystkich punktów,

których współrz

ę

dne spełniaj

ą

form

ę

zdaniow

ą

F(x, y): x < –2

⇒

y – 3x > 6.

Odpowiedzi

(Kod: K1_D1_R_K2B)

1. a) Zdanie fałszywe;
b) zdanie fałszywe.
2. Wyra

ż

enie nie jest tautologi

ą

.

3. a)

a

3

a

:

R

a

2

<

∈

∃

(zdanie prawdziwe);

b)

3

k

k

:

R

k

=

∈

∀

(zdanie fałszywe).

4. a)

Kwadrat nie jest figurą osiowosymetryczną lub prosta nie jest figurą

środkowosymetryczną

.

b)

Wieloryb jest ssakiem i płotka nie jest rybą

.

c)

]

1

x

x

x

[

:

R

x

3

<

∧

≤

∈

∀

.

5. D = R – {–5}; x ∈{0}.
6.