1

Pytanie nr 10. Czy prawdą jest, że zgodnie z modelem Bohra atomu wodoru, w stanie
podstawowym (n=1):
a) Energia potencjalna elektronu ma największą wartość.
b) Prędkość elektronu ma największą wartość.
c) Promień orbity elektronu ma najmniejszą wartość.
d) Moment pędu elektronu jest h/4π.
e) Elektron promieniuje fale elektromagnetyczne. Uzasadnij odrzucenie stwierdzeń
fałszywych.

Poprawne odpowiedzi: a), b), c),

Odpowiedź d) jest nieprawidłowa, ponieważ moment pędu L:

= ℏ =

ℎ

2

h – stała Plancka (6,626·10

-34

J·s),

n – numer orbity
Dla n=1 mamy:

= 1 ∙

ℎ

2

≠

ℎ

4

Odpowiedź e) odrzucamy, ponieważ wg modelu Bohra atom promieniuje jeśli elektron
przeskakuje z orbity dalszej od jądra na orbitę bliżej jądra. W atomie wodoru mamy tylko
jedną orbitę.

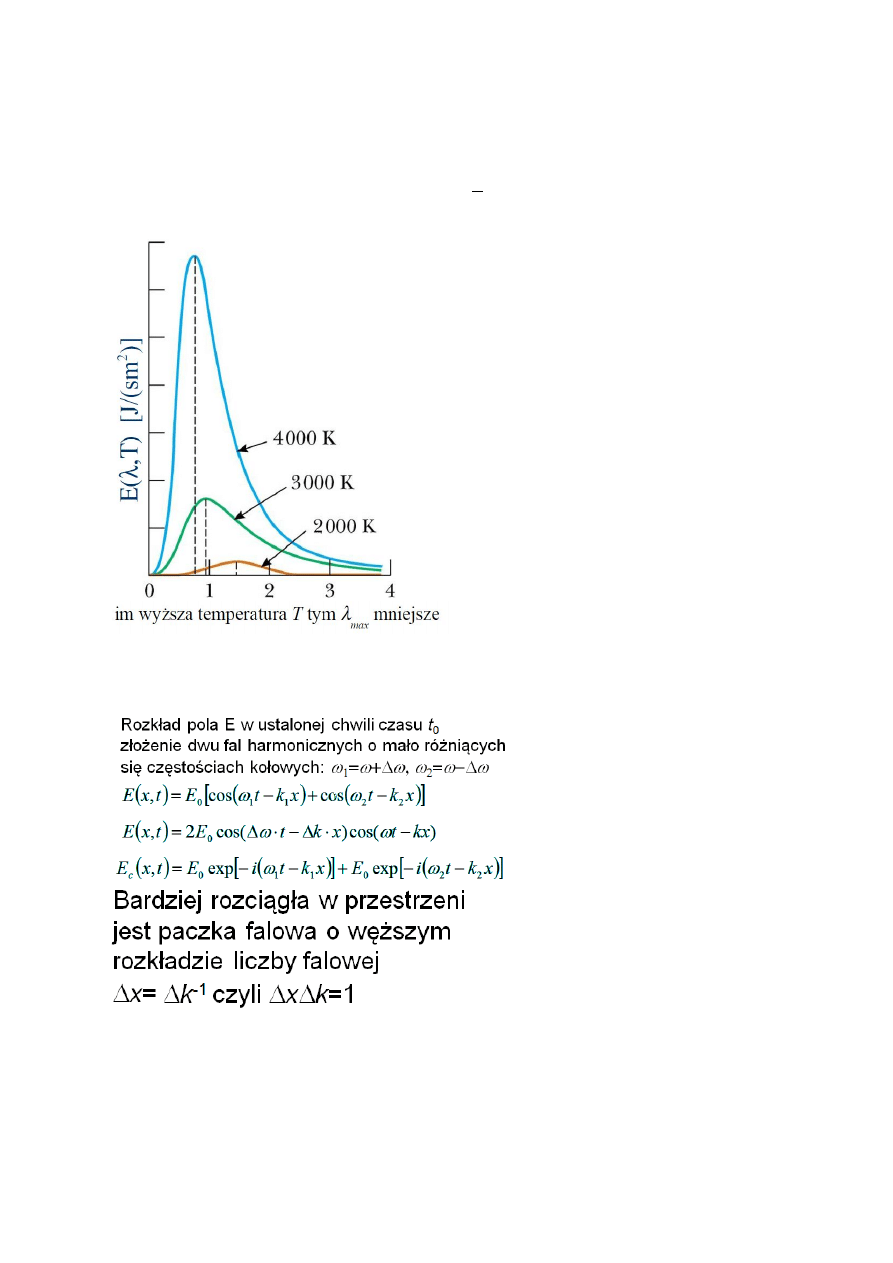
Zagadnienie nr 2. Promieniowanie termiczne – prawa Kirchhoffa, Stefana-Boltzmana,
Wiena

Zdolność emisyjna E

T

ciała doskonale czarnego jest proporcjonalna do czwartej potęgi

temperatury T.

Stała Boltzmana

2

Prawo Wiena – długość fali odpowiadająca maksymalnej zdolności emisyjnej ciała doskonale
czarnego jest równa:

=

b = 0,2898·10

-2

m·K (stała Wiena)

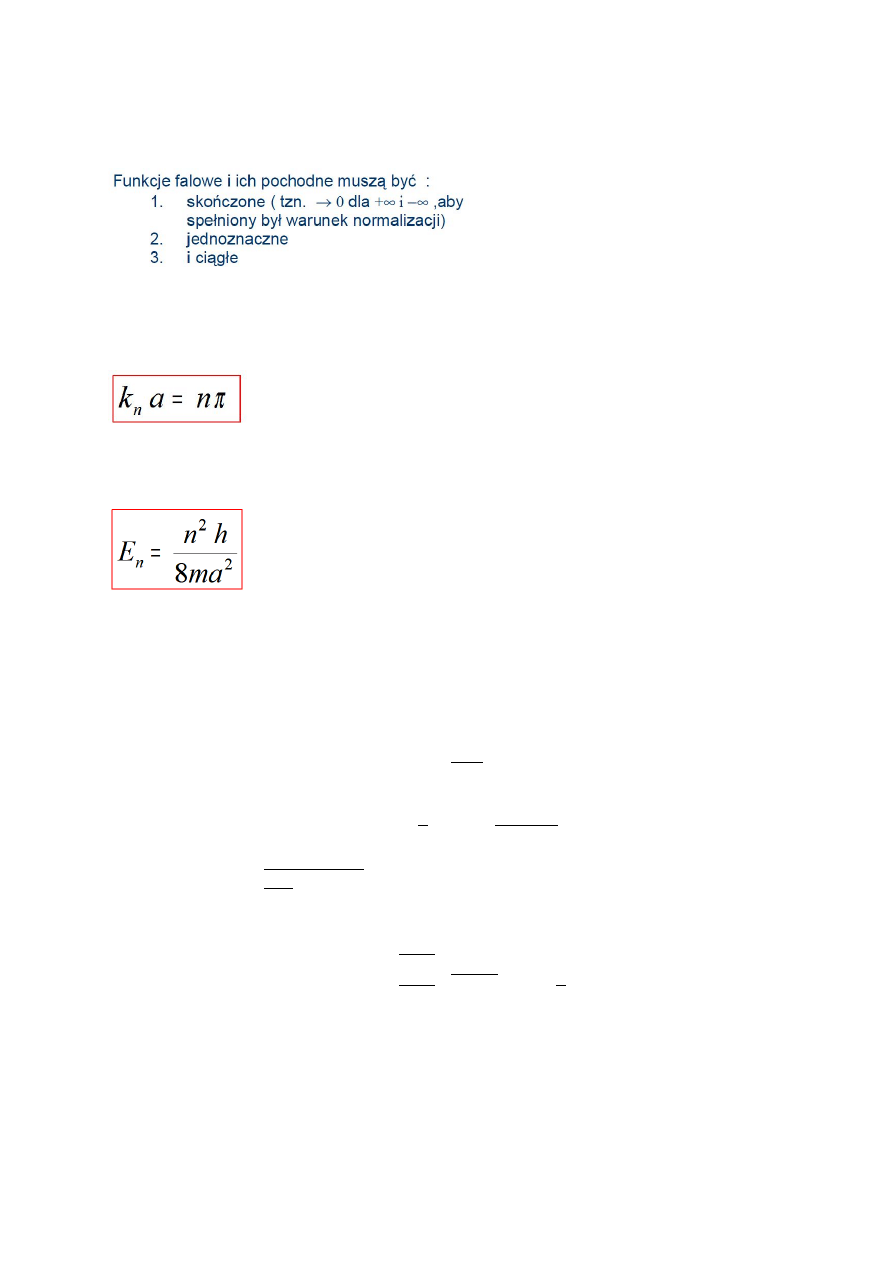
Zagadnienie nr 9. Złożenie fal o różnych częstościach, związek między szerokością
rozkładu liczby falowej a rozciągłością paczki falowej.

Na przykładzie pola elektrycznego:

Gdzie Δx to rozciągłość paczki falowej, a Δk – rozkład liczby falowej.

3

Zagadnienie nr 16. Warunki na funkcję falową, dyskretne wartości energii cząstki
związanej jako wynik rozwiązania równania Schrodingera.

Rozwiązując równanie Schrodingera dla nieskończenie głębokiej studni potencjału ( o
szerokości od 0 do a ) można otrzymać funkcję falową:

( , ) =

(

) exp(−

)

Warunek brzegowy: fale powinny zanikać na ściankach: (

0) = 0 ( ) = 0

Zatem sin(ka)=0

Energia: E=p

2

/(2m)

p – pęd, m-masa cząstki

Ponieważ pęd: p=hk/(2π)
Podstawiając pod wzór na energię otrzyma się:

Dla n=1,2,3,….

Wartości energii są zatem dyskretne.

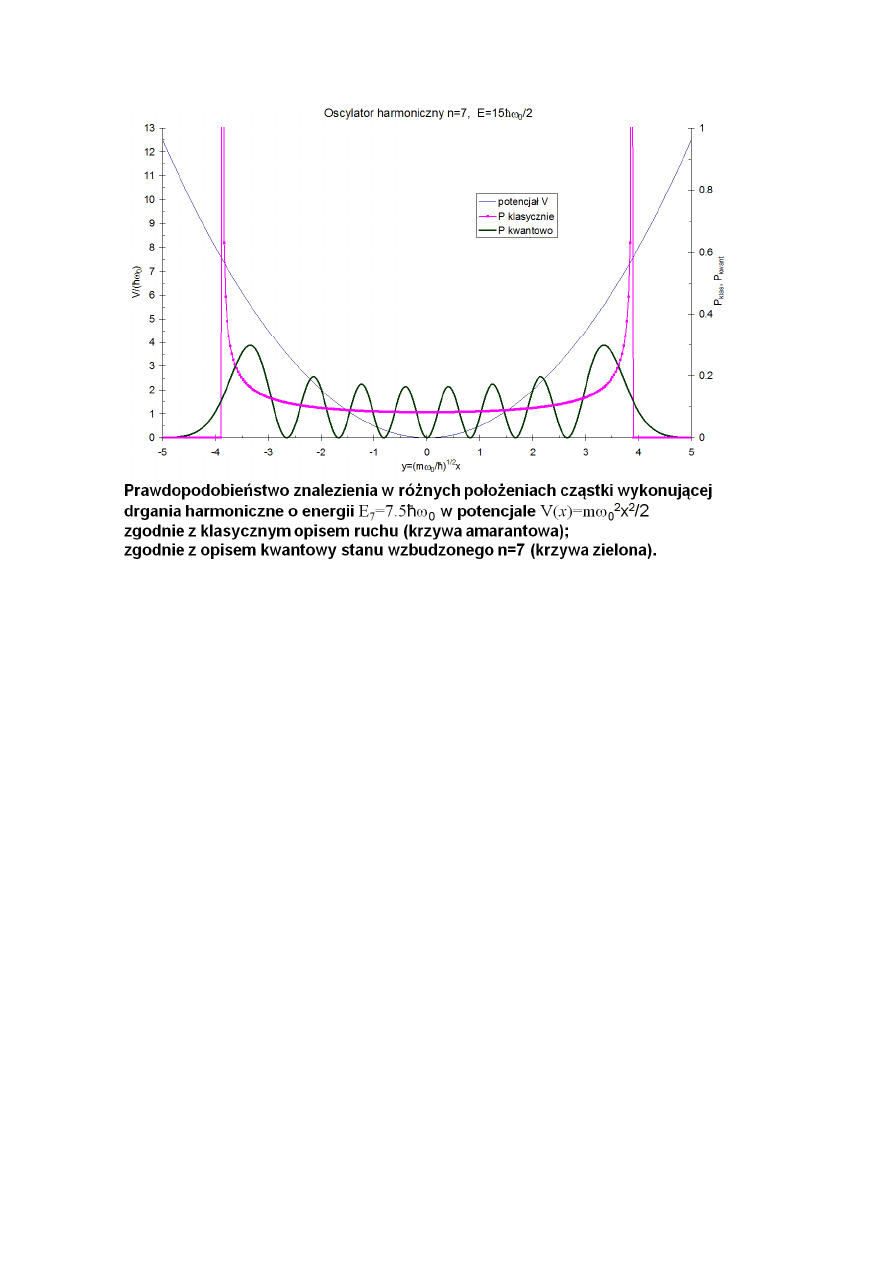
Zagadnienie nr 23. Drgania zerowe oscylatora harmonicznego, nieokreśloność pędu i
położenia, porównanie z teorią klasyczną.

Drgania zerowe odpowiadają najniższej wartości energii oscylatora harmonicznego. Zgodnie
z opisem kwantowym niemożliwe jest aby E=0.

=

ℏ

2

Kolejne poziomy energii oscylatora harmonicznego są równe:

=

+

1
2

ℏ

=

2

Stąd amplituda:

ℏ

(2 + 1)

Iloczyn pędu i nieokreśloności położenia (dla n=0):

=

ℏ

ℏ

= ℏ >

ℏ
2

(zgodnie z zasadą nieoznaczoności)

W opisie klasycznym energię obliczamy ze wzoru: E=0.5kx

0

2

. Zakładamy więc, że możliwe

są zerowe wartości energii.

4

Zagadnienie nr 30. Spin elektronu, doświadczenie Sterna-Gerlacha, rozszczepienie linii
widmowych. Liczba stanów elektronowych w atomie.

Spin – własny moment pędu elektronu.

Doświadczenie Sterna-Gerlacha – eksperyment przeprowadzony w początku XX wieku,
będący dowodem na istnienie kwantowania momentu pędu.

Doświadczenie to w oryginalnej wersji polegało na przepuszczeniu wiązki atomów srebra
przez niejednorodne pole magnetyczne i obserwacji obrazu wiązki na ekranie (np. kliszy
fotograficznej).

Atomy srebra mają niezerowy własny moment pędu (spin) i związany z nim moment
magnetyczny. Oddziaływanie tego momentu magnetycznego z zewnętrznym polem
magnetycznym zmienia tor ruchu atomu. Zmiana ta zależy od orientacji wektora momentu
pędu w przestrzeni, a dokładniej od wartości rzutu tego wektora na kierunek zewnętrznego
pola. Ponieważ kierunki spinów atomów opuszczających piec są przypadkowe, to, zgodnie z
mechaniką klasyczną, wartość tego rzutu może przyjąć dowolną wartość ograniczoną tylko
przez wartość (długość wektora) momentu magnetycznego. Tym samym odchylenie toru
atomu może być dowolne, pomiędzy wartościami skrajnymi odpowiadającymi ustawieniom
spinu równolegle i antyrównolegle do pola. Mechanika klasyczna przewiduje więc, że obraz
wiązki na ekranie powinien być jedną plamą rozciągniętą wzdłuż kierunku pola
magnetycznego.

Według mechaniki kwantowej przewidywanie wyniku eksperymentu jest inne: rejestracja
odchylenia toru atomu (jego położenia na ekranie) jest aktem pomiaru składowej momentu

5

pędu wzdłuż kierunku zewnętrznego pola. Pomiar taki może dać wynik tylko z pewnego
dyskretnego zbioru możliwych wartości. W wypadku cząstki o spinie 1/2 możliwe są dwa
wyniki takiego pomiaru: +1/2 i –1/2. Oznacza to, że atomy srebra powinniśmy rejestrować
tylko w dwóch punktach ekranu, a w praktyce, że względu na skończone rozmiary poprzeczne
wiązki i nieunikniony rozrzut prędkości atomów, w dwóch obszarach.

W doświadczeniu faktycznie obserwuje się na ekranie dwie plamy, zgodnie z
przewidywaniem mechaniki kwantowej.

Ogólnie: otrzymanie dwóch wartości składowej z momentu magnetycznego.

Liczba stanów elektronowych w atomie jest równa 2n

2

. Jest więc 2n

2

kombinacji liczb

kwantowych.