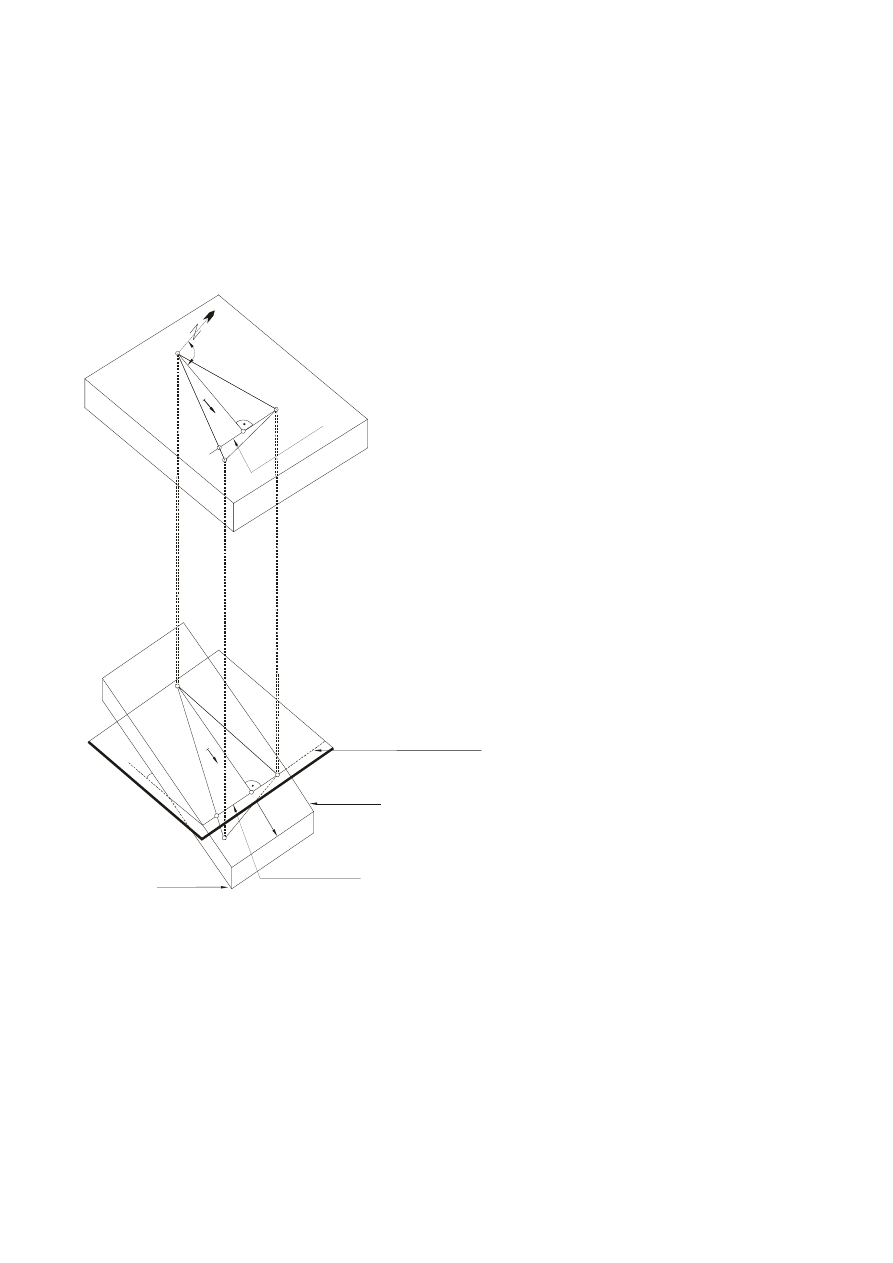
A

B

C

P

2

P

3

P

1

ε

Pła

szc

zyz

na p

ozio

ma

Lin

ia u

pa

du

α

Lin

ia

roz

cią

gło

ści

Lin

ia u

pa

du

α

Lin

ia

up

ad

u

H

A

H

B

H

C

H

P1

H

P2

H

P3

Po

kła

d

Strop warstwy

Spąg warstwy

Linia rozciągłości

Pła

szc

zyz

na p

ozio

ma

P

Ką

t up

ad

u α

Krawędź przecięcia płaszczyzny

poziomej P z płaszczyzną stropu

warstwy - linia o rzędnej

H =H =H =H H

P

P2

P3

B=

P1

Objaśnienia oznaczeń:
A, B, C – otwory wiertnicze, którymi nawiercono
warstwę geologiczną
H

A,

H

B,

B

C

– rzędne wysokościowe nawierconej

warstwy geologicznej

L

A,

L

B,

L

C

– odległości pomiędzy otworami

P – płaszczyzna pozioma

H

p

– rzędna wysokościowa płaszczyzny poziomej

P

1,

P

2

– punkty przecięcia się boku trójkąta

wyznaczonego przez otwory wiertniczej na
nachylonej płaszczyźnie stropu lub spągu
warstwy z krawędzią przecięcia się
płaszczyzny poziomej z płaszczyzną
nachylonego stopu lub spągu warstwy

P

3

– rzut prostopadły na linię rozciągłości punktu

na osi otworu, z którego wyznacza się
elementy zalegania warstwy

φ – kąt nachylenia stropu lub spągu warstwy (na

bokach trójkąta ABC)

∆h – różnice rzędnych wysokościowych
α – kąt upadu warstwy
ω – azymuty
L

AP1,

L

AP2,

L

AP3

– odcinki poziome zawarte

pomiędzy punktami P

1,

P

2,

P

3

a otworem, z

którego wyznacza się elementy zalegania
spągu lub stropu warstwy geologicznej

X,Y– współrzędne sytuacyjne otworów

wiertniczych

L

A P2

L

A C

Otw.A

Otw.C

Powierzchnia terenu

H

A

H

C

P

2

H

P3

∆h

AP

3

∆h

AC

φ

AC

φ

AC

Strop

Spąg

L

AP1

L

AB

Otw.A

Otw.B

Powierzchnia terenu

H

A

H

B

P

1

H

P3

∆h

AP

3

∆h

AB

φ

AB

φ

AB

Strop

Spąg

Szkic

Dane do obliczeń

X

A

Y

A

A

H

A

X

B

Y

B

B

H

B

X

C

Y

C

C

H

C

H H

P

Długość L

AP1

Długość L

AP2

Wzór Obliczenia Wyniki Wzór Obliczenia Wyniki

L

AB

L

AP1

L

AC

L

AP2

Azymut boku

ω

AB

Azymut

boku

ω

AC

Wzór Obliczenia Wyniki

Wzór Obliczenia Wyniki

ω

AB

ω

AC

Różnice rzędnych wys.

∆h

AB

; ∆h

AC

; ∆h

AP

Wzory Obliczenia

H

A

H

B

∆h

AB

= H

A

- H

B

∆h

AB

H

A

H

C

∆h

AC

= H

A

– H

C

∆h

AC

H

A

H

P

∆h

AP

= H

A

– H

P

∆h

AP

Długości boków l

AB

i l

AC

Wzory

Obliczenia Wyniki

Y

B

Y

A

∆y

AB

∆y

2

AB

X

B

X

A

∆x

AB

∆x

2

AB

l

AB

Y

C

Y

A

∆y

AC

∆y

2

AC

X

C

X

A

∆x

AC

∆x

2

AC

l

AC

A

C

A

C

AC

X

X

Y

Y

tg

−

−

=

ω

CA

CA

X

Y

∆

∆

A

B

A

B

AB

X

X

Y

Y

tg

−

−

=

ω

BA

BA

X

Y

∆

∆

AB

AB

AP

AP

L

h

h

L

⋅

∆

∆

=

1

AB

AP

h

h

∆

∆

AC

AC

AP

AP

L

h

h

L

⋅

∆

∆

=

2

AC

AP

h

h

∆

∆

()

(

)

2

2

A

B

A

B

AB

X
X

Y
Y

L

−
+
−
=

()

(

)

2

2

A

C

A

C

AC

X
X

Y
Y

L

−
+
−

=

Współrzędne punktów P

1

i P

2

Wzory Obliczenia

Wynik

X

A

L

AP1

±cosω

AB

±∆X

P1

X

P1

Y

A

L

AP1

±sinω

AB

±∆Y

P1

Y

P1

X

A

L

AP2

±cosω

AC

±∆X

P2

X

P2

Y

A

L

AP2

±sinω

AC

±∆Y

P2

Y

P2

Azymut linii rozciągłości ω

P1 P2

Azymut linii upadu ω

A P3

Wzór Obliczenia

Wynik

Wzór Obliczenia

Wynik

+90°

±180°

Kąt β

1

Kąt β

2

Kąt β

Wzór Obliczenia Wzór Obliczenia

Wzór Obliczenia

β

1

β

2

β

1

β

2

β

Długość linii upadu L

AP3

Wzory Obliczenia

Wynik

Kąt upadu

Wzór Obliczenia

Wynik

Współrzędne punktu P

3

Wzory Obliczenia

Wynik

Obliczył:

AB

AP

A

P

L

X

X

ω

cos

⋅

±

=

1

1

AB

AP

A

P

L

Y

Y

ω

sin

⋅

±

=

1

1

AC

AP

A

P

L

X

X

ω

cos

⋅

±

=

2

2

AC

AP

A

P

L

Y

Y

ω

sin

⋅

±

=

2

2

3

AP

ω

1

2

1

2

2

1

P

P

P

P

P

P

X

X

Y

Y

tg

−

−

=

ω

1

2

1

2

P

P

P

P

X

Y

∆

∆

2

1P

P

ω

°

±

°

+

=

180

90

2

1

3

P

P

AP

ω

ω

2

1P

P

ω

2

1

β

β

β

+

=

3

2

AP

AC

ω

ω

β

−

=

AB

AP

ω

ω

β

−

=

3

1

3

AP

ω

AB

ω

AC

ω

3

AP

ω

1

AP

L

1

1

3

β

cos

⋅

=

AP

AP

L

L

1

β

cos

3

AP

L

2

2

3

β

cos

⋅

=

AP

AP

L

L

2

AP

L

2

β

cos

3

AP

L

3

3

AP

AP

AP

L

h

tg

∆

=

α

AP

h

∆

3

AP

L

3

AP

AP

L

h

∆

α

α

=

3

AP

3

AP

L

A

X

3

3

3

AP

AP

A

P

L

X

X

ω

cos

⋅

±

=

3

3

3

AP

AP

A

P

L

Y

Y

ω

sin

⋅

±

=

A

Y

3

AP

ω

cos

±

3

AP

ω

sin

±

3

P

X

3

P

Y