Zadania projektowe z Matlaba:



Uwagi:
Każdy otrzymuje indywidualny zbiór z danymi pomiarowymi.
Na wykresach w zad. 1 i 2 przyjąć wielkość czcionki 14pt (tytuł, oznaczenia osi, podziałka
liczbowa, napisy na rysunku) i grubość linii (charakterystyki) 2pt.

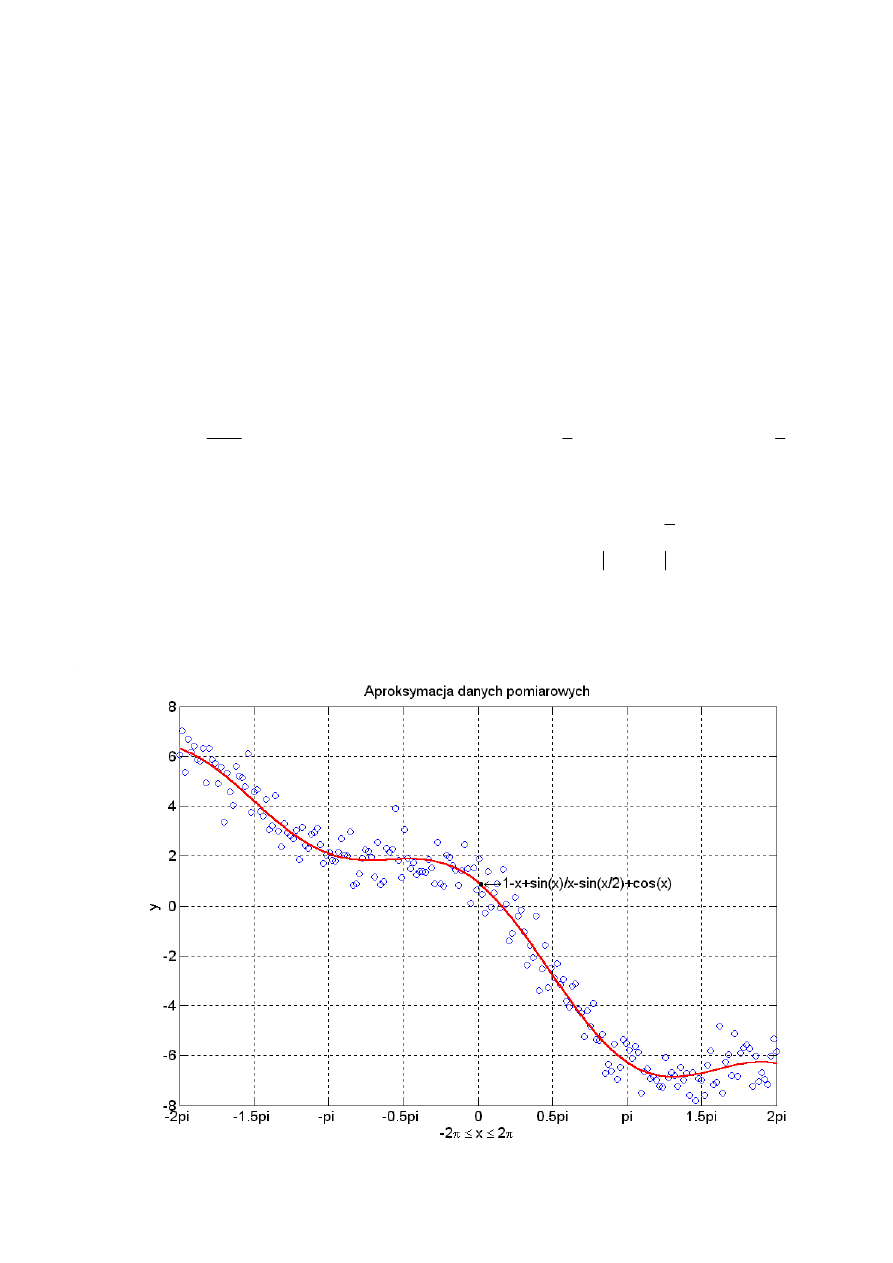
Zad. 1. Aproksymacja danych pomiarowych. (4 punkty)

Przeprowadzono n pomiarów wartości dwóch wielkości fizycznych x i y. Wyniki

pomiarów zawarte są w wektorach x i y w zbiorze *.mat. Korzystając z metody
najmniejszych kwadratów znaleźć współczynniki funkcji przybliżającej zależność między
zmiennymi x i y.

Ogólna postać funkcji aproksymującej:

( )

( )

( )

( )

( )

( )

( )













+

+

+













+

+

+

+

+

+

+

=

2

cos

2

cos

cos

2

sin

2

sin

sin

cos

sin

sin

11

10

9

8

7

6

5

4

3

2

1

x

a

x

a

x

a

x

a

x

a

x

a

x

x

a

x

x

a

x

x

a

x

a

a

y

(Zbiór współczynników indywidualny)

Wartości współczynników podać z rozdzielczością 0,1.

Obliczyć wartość odchylenia średniokwadratowego, zgodnie ze wzorem:

( )

(

)

∑

=

−

=

n

i

i

i

x

f

y

n

1

1

δ

Znaleźć największe odchylenia od prostej aproksymującej

( )

i

i

i

x

f

y

−

= max

max

δ

Sporządzić wykres funkcji y = f(x). Przyjąć zakres zmian wielkości x od –2

π do 2π.

Nanieść na wykres punkty pomiarowe. Oznaczyć osie. Zamieścić na wykresie równanie
funkcji aproksymującej z uwzględnieniem obliczonych wartości współczynników.

Zastosować oznaczenia, jak na rysunku.

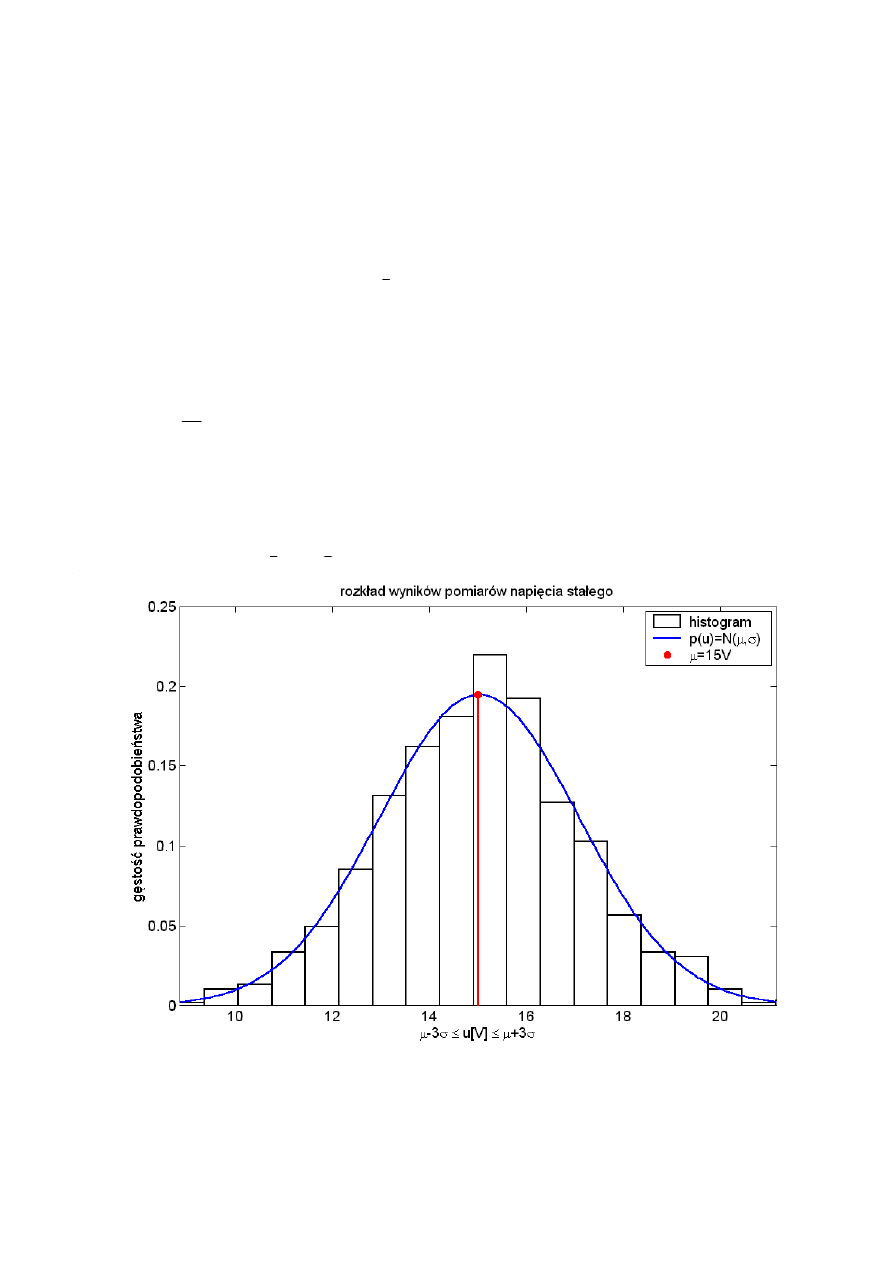
Zad. 2. Analiza statystyczna wyników pomiarów. (4 punkty)

Wykonano serię 1000 pomiarów wartości napięcia stałego (wektor u w pliku *.mat).

Wskutek istnienia błędów przypadkowych wyniki pomiarów są rozproszone wokół wartości
rzeczywistej U

r

.

Wiedząc, iż napięcie mierzone jest zmienną losową o rozkładzie normalnym obliczyć

wartości parametrów statystycznych opisujących zmienną losową u:

- wartość minimalną u

min

i maksymalną u

max

,

- medianę m

e

,

- wartość oczekiwaną (średnią)

x

,

- odchylenie

standardowe

σ.

Wyniki obliczeń statystycznych podać w sprawozdaniu z rozdzielczością 1mV.

Sporządzić histogram wyników pomiarów dla 20 podprzedziałów o jednakowej

szerokości między u

min

i u

max

. Histogram powinien spełniać warunek normalizacyjny:

u

h

n

i

i

∆

=

∑

=

1

1

, gdzie h

i

– wysokość słupka, n – liczba słupków,

∆u – szerokość podprzedziału.

Sąsiednie słupki powinny do siebie przylegać.
Na ten sam wykres nanieść krzywą rozkładu prawdopodobieństwa ciągłej zmiennej

losowej o rozkładzie normalnym i parametrach takich jakie zostały wyznaczone dla zmiennej
losowej u. Linią pionową zaznaczyć na wykresie wartość oczekiwaną.

Sformatować wykres zgodnie z poniższym rysunkiem. Przyjąć na wykresie zakres zmian

napięcia mierzonego [

x

-3

σ...

x

+3

σ]. Kolory linii jak na rysunku.

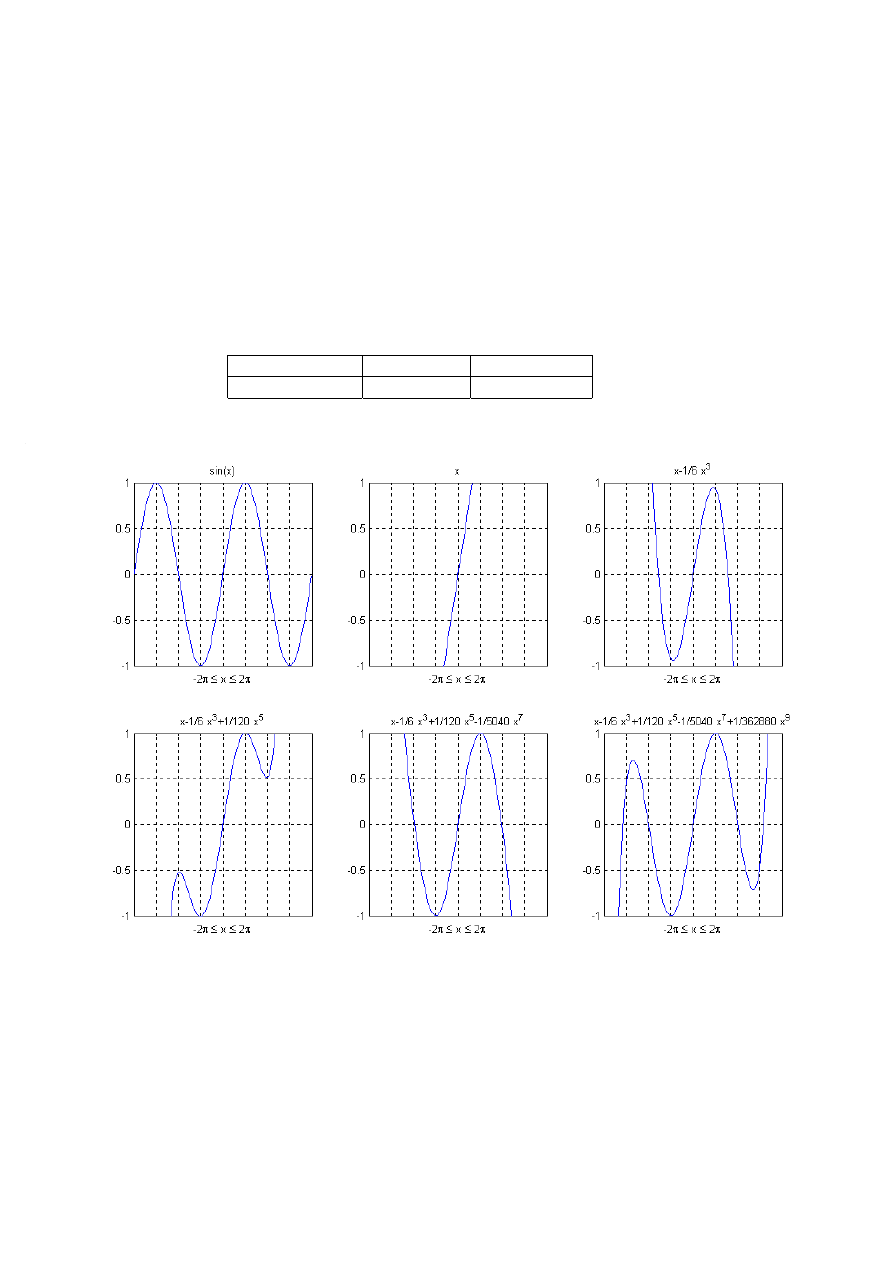
Zad. 3. Rozwijanie funkcji w szereg Taylora. (3 punkty)

Rozwinąć funkcję y = f(x) w szereg Taylora w otoczeniu punktu x

0

= 0.

1) y = sin(x)/x
2) y = cos(x)
3) y = sinh(x)
4) y = sinh(x)/x
5) y = sinh(x)/sin(x)

6) y = sinh(x)/cos(x)
7) y = cosh(x)
8) y = exp(x)
9) y = sin(x)/exp(x)
10) y = cos(x)/exp(x)

11) y = log(x+1)
12) y = log(x+1)/sin(x)
13) y = log(x+1)/cos(x)
14) y = log(x+1)/sinh(x)
15) y = log(x+1)/cosh(x)

Zamieścić w jednym oknie wykres funkcji y = f(x) oraz pięć wykresów rozwinięcia tej

funkcji w szereg Taylora z uwzględnieniem różnej liczby składników sumy w szeregu.

Rozmieszczenie wykresów w oknie powinno być następujące:

Funkcja y =f(x) 1

składnik 2

składniki

3 składniki 4

składniki 5

składników

Zastosować formatowanie zgodnie z poniższym rysunkiem – przykład dla funkcji y = sin(x).
Przyjąć zakres zmian wielkości x od –2

π do 2π. Nanieść na wykres punkty pomiarowe.