Obliczanie rozp

Obliczanie rozp

ł

ł

yw

yw

ó

ó

w pr

w pr

ą

ą

d

d

ó

ó

w

w

w sieciach otwartych

w sieciach otwartych

- Metoda liczb zespolonych

- Pierwsze prawo Kirchhoffa

2 / 31

Podstawowe

Podstawowe

zale

zale

ż

ż

no

no

ś

ś

ci

ci

i

i

okre

okre

ś

ś

lenia

lenia

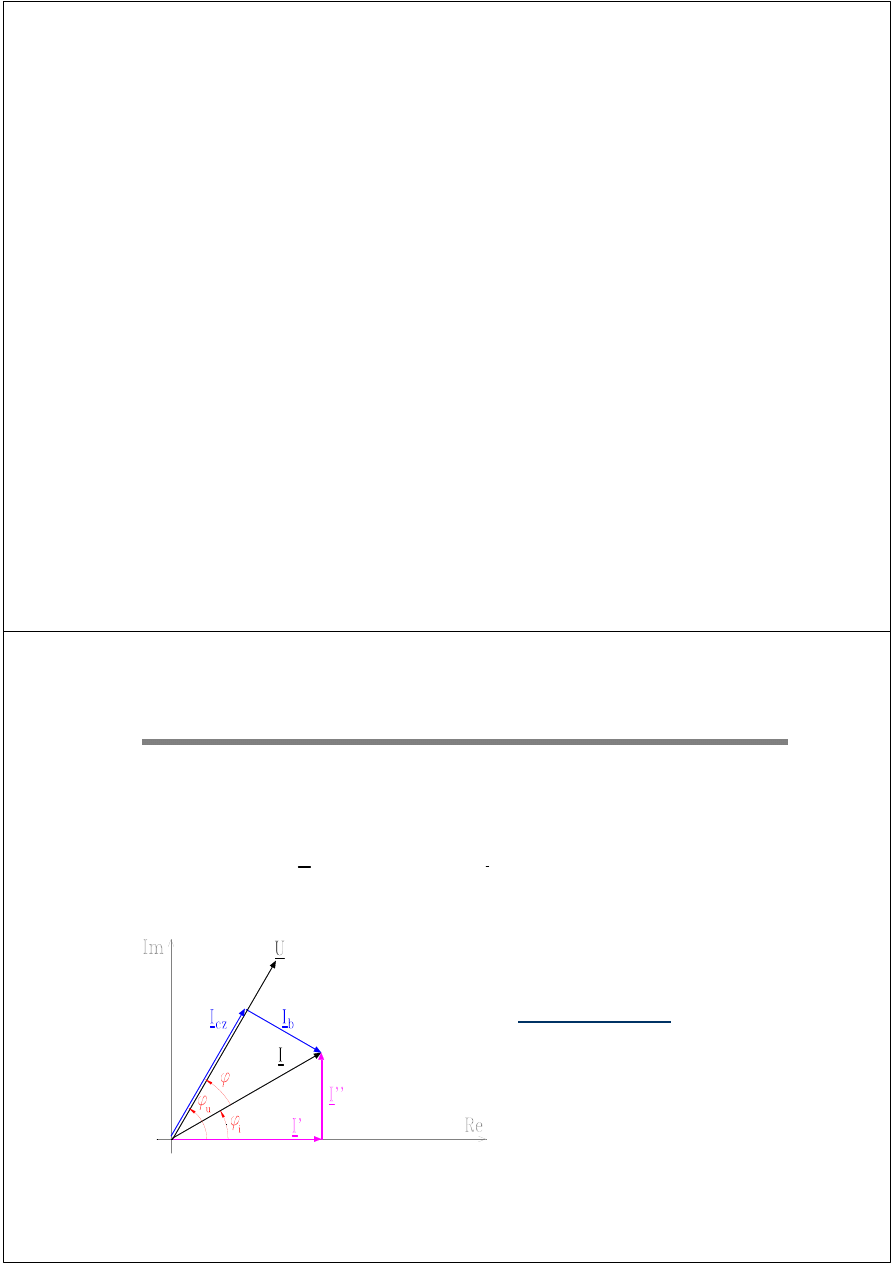
Składowe prądu:

Czynna

I

cz

= I cos

ϕ

Bierna

I

b

= I sin

ϕ

Rzeczywista

I’ = I cos

ϕ

i

Urojona

I” = I sin

ϕ

i

u

j

f

f

U

U e

ϕ

=

i

j

I Ie

ϕ

=

Napięcie i prąd w węźle odbiorczym wyrażają się wzorami:

U

f

, I – wartości skuteczne napięcia i prądu

φ

u

, φ

i

– fazy napięcia i prądu

3 / 31

u

u

i

i

j

j(

)

j

f

f

f

j

f

f

f

S 3U I

3U e

Ie

3U Ie

3U Ie

3U Icos

j3U Isin

P jQ

ϕ

ϕ −ϕ

∗

− ϕ

ϕ

=

⋅ =

⋅

=

=

=

=

ϕ +

ϕ =

= +

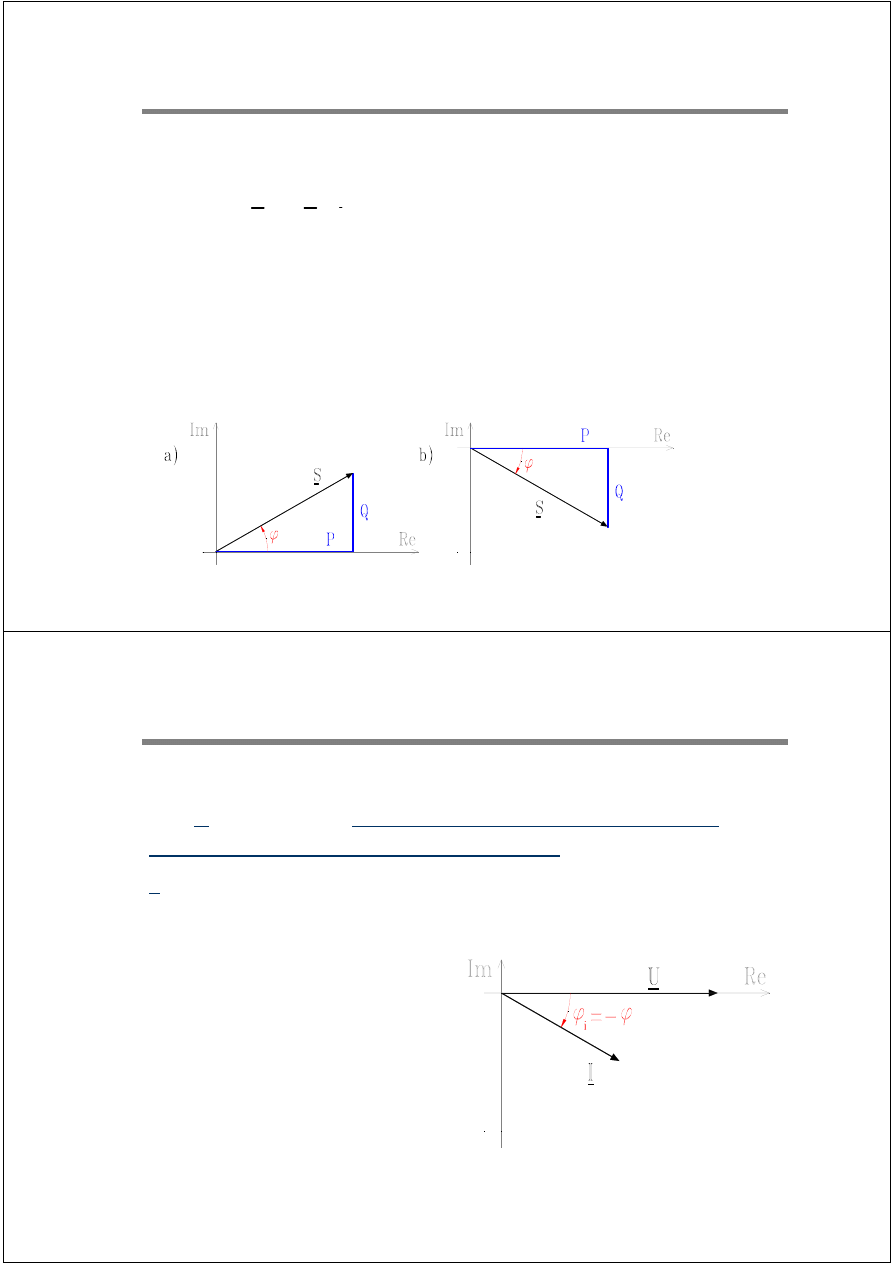
Przy obciążeniu indukcyjnym kąt

ϕ jest dodatni i moc bierna jest

również dodatnia, przy obciążeniu pojemnościowym kąt

ϕ i moc Q

są ujemne.

Podstawowe zale

Podstawowe zale

ż

ż

no

no

ś

ś

ci i okre

ci i okre

ś

ś

lenia

lenia

Moc zespolona

4 / 31

Podstawowe zale

Podstawowe zale

ż

ż

no

no

ś

ś

ci i okre

ci i okre

ś

ś

lenia

lenia

Jeżeli wektor napięcia położony jest w osi rzeczywistych,
czyli U = U i

ϕ = - ϕ

i

, wówczas składowa urojona prądu równa

jest składowej biernej z przeciwnym znakiem:
I = I’ - j I” = I cos

ϕ

i

– j I sin

ϕ

i

= I cos(-

ϕ) - j I sin (-ϕ)

I’ = I cos

ϕ

i

= I cos

ϕ = I

cz

- I” = - I sin

ϕ

i

= I sin

ϕ = I

b

Podsumowując:

Przy obciążeniu indukcyjnym
ϕ > 0, Q > 0, I” < 0
Przy obciążeniu pojemnościowym
ϕ < 0, Q < 0, I” > 0

5 / 31

Za

Za

ł

ł

o

o

ż

ż

enia do oblicze

enia do oblicze

ń

ń

Obliczenia rozpływu prądów rozpoczyna się od wyznaczenia prądów

odbiorów.

Przyjmuje się następujące założenia:
1. W każdym węźle panuje napięcie znamionowe:

U

α

= U

αn

2. Wektor napięcia położony jest w osi rzeczywistych:

U

α

= U

α

,

ϕ

i

α

=

ϕ

α

Przy takich założeniach:

I

α

= I

α

(cos

ϕ

α

- j sin

ϕ

α

)

gdzie:

n

P

I

3 U cos

α

α

α

=

φ

α - numer węzła
P

α ,

cos

ϕ

α

-dane

6 / 31

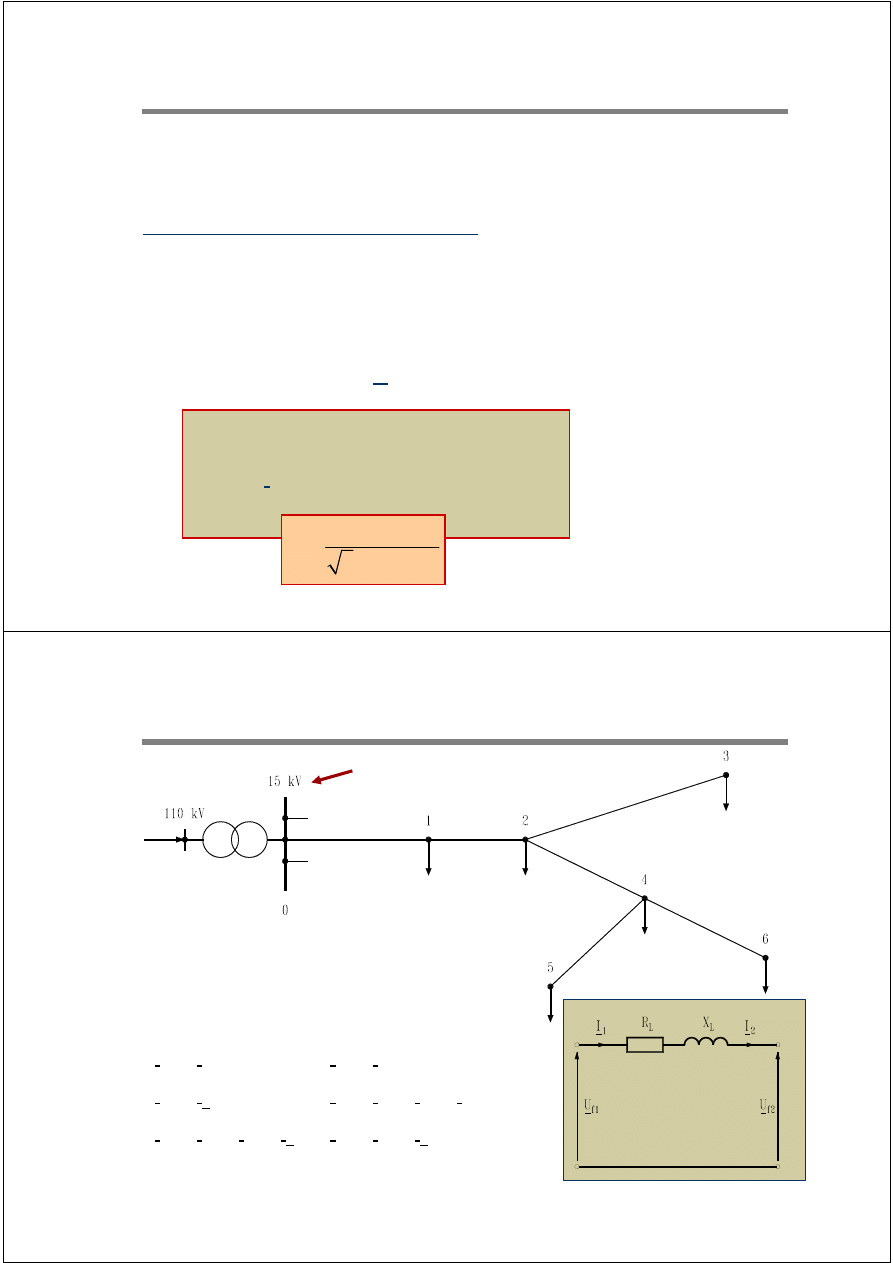
Rozp

Rozp

ł

ł

yw pr

yw pr

ą

ą

d

d

ó

ó

w w sieciach I i II rodzaju

w w sieciach I i II rodzaju

1. Obliczenie prądów odbiorów
2. Obliczenie prądów w gałęziach sieci

I

46

= I

6

I

54

= I

5

I

24

= I

46

+ I

54

+ I

4

I

23

= I

3

I

12

= I

23

+ I

24

+ I

2

I

01

= I

12

+ I

1

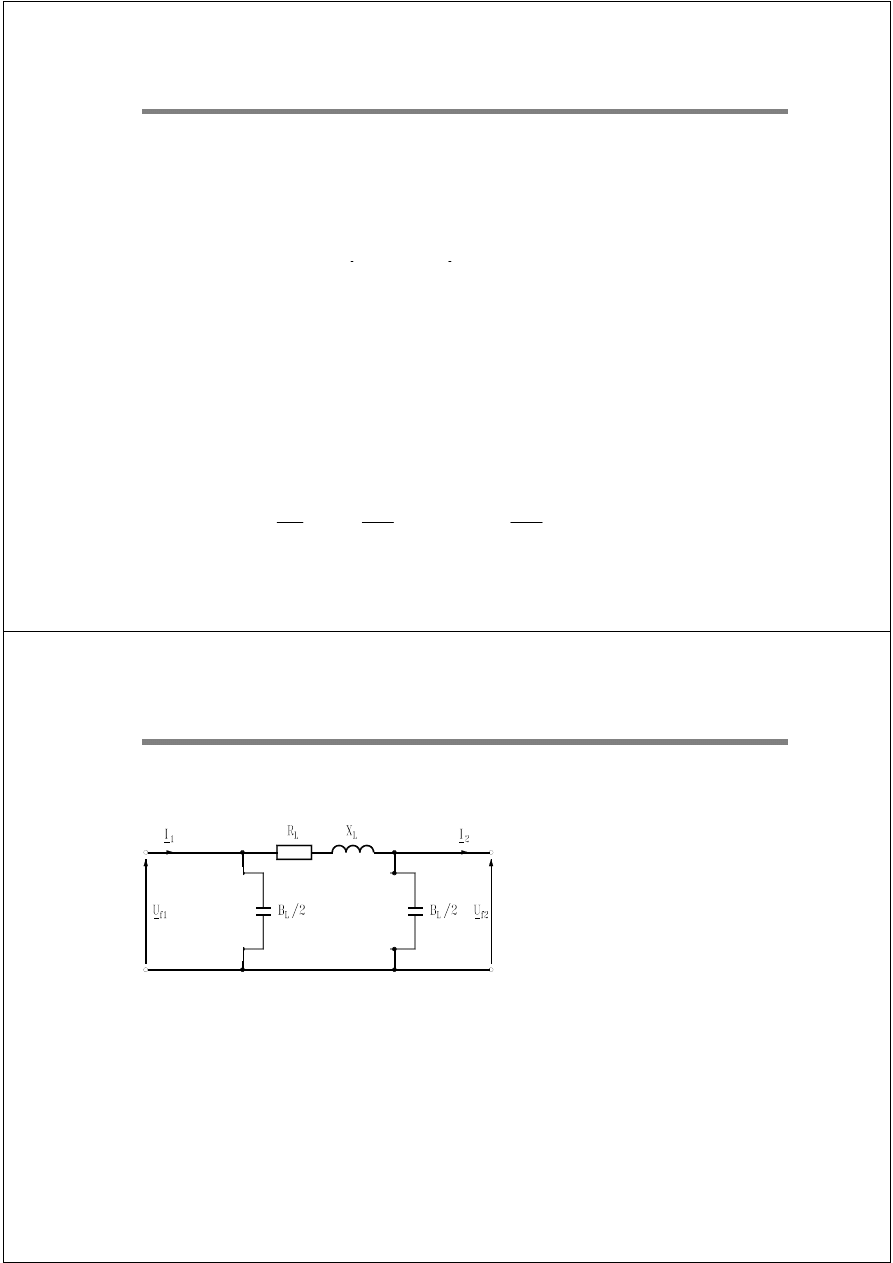
Schemat zastępczy gałęzi grafu

7 / 31

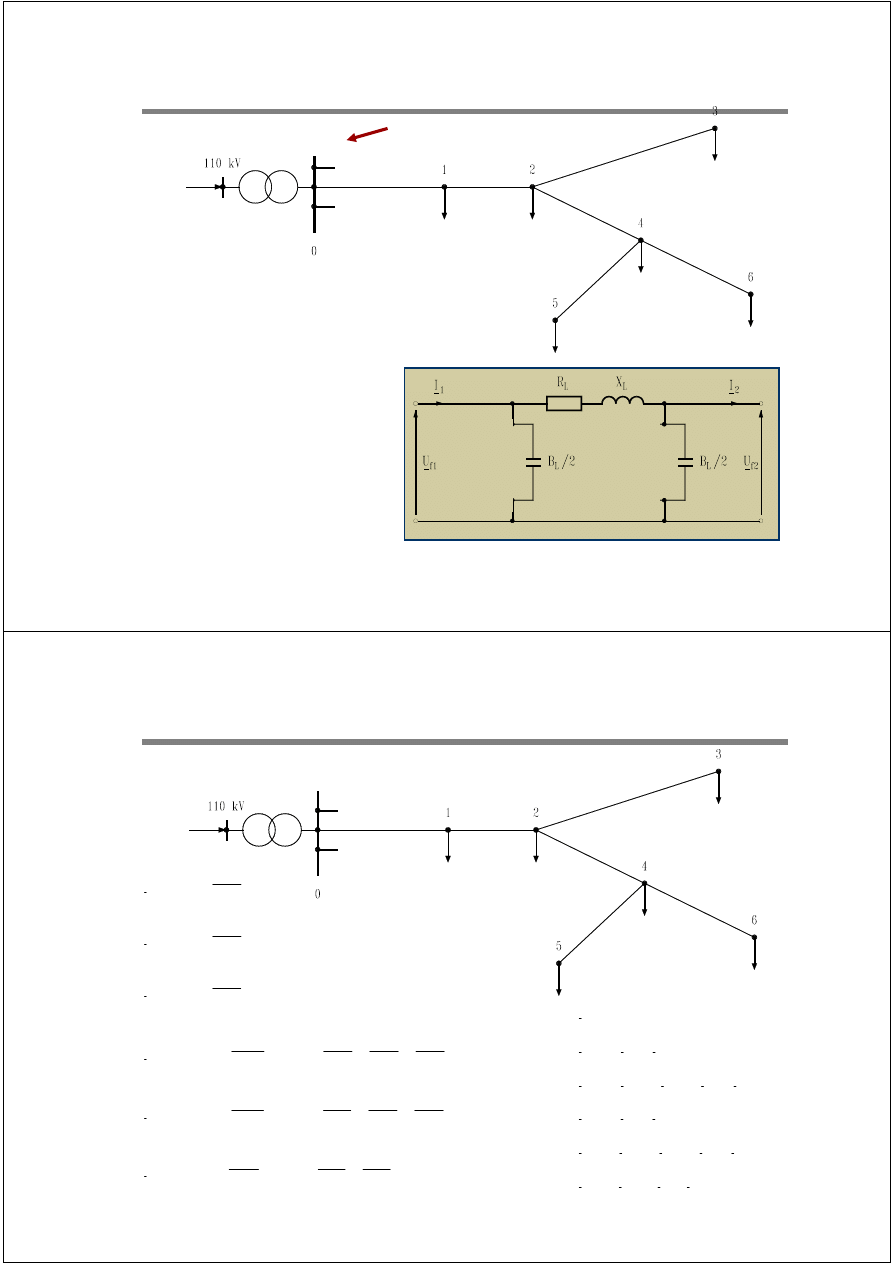
Rozp

Rozp

ł

ł

yw pr

yw pr

ą

ą

d

d

ó

ó

w w sieciach III rodzaju

w w sieciach III rodzaju

30 kV

1. Obliczenie prądów odbiorów

2. Obliczenie prądów

pojemnościowych

3. Obliczenie prądów w

gałęziach sieci

Schemat zastępczy gałęzi grafu sieci

8 / 31

Rozp

Rozp

ł

ł

yw pr

yw pr

ą

ą

d

d

ó

ó

w w sieciach III rodzaju

w w sieciach III rodzaju

30 kV

4

45

46

24

fn

fn

c4

B

B

B

B

I

jU

jU

2

2

2

2

α

⎛

⎞

=

=

+

+

⎜

⎟

⎝

⎠

∑

2

23

12

24

fn

fn

c2

B

B

B

B

I

jU

jU

2

2

2

2

α

⎛

⎞

=

=

+

+

⎜

⎟

⎝

⎠

∑

1

01

12

fn

fn

c1

B

B

B

I

jU

jU

2

2

2

α

⎛

⎞

=

=

+

⎜

⎟

⎝

⎠

∑

46

fn

c6

45

fn

c5

23

fn

c3

B

I

jU

2

B

I

jU

2

B

I

jU

2

=

=

=

6

c6

46

54

5

c5

24

46

54

4

c4

23

3

c3

12

23

24

2

c2

01

12

1

c1

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I I

= +
= +
=

+

+ +

= +

=

+

+ +

=

+ +

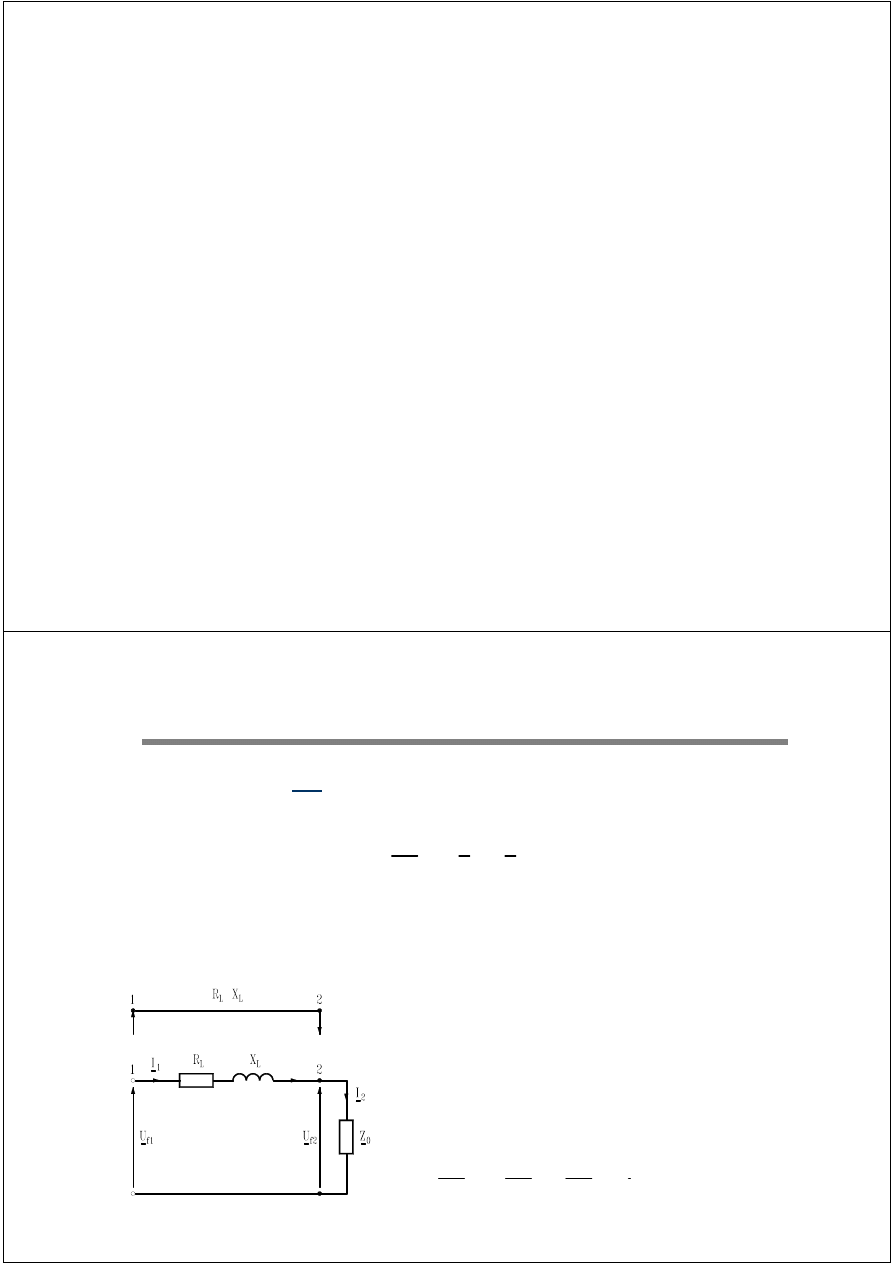
Obliczanie spadk

Obliczanie spadk

ó

ó

w i strat napi

w i strat napi

ę

ę

cia

cia

w sieciach otwartych

w sieciach otwartych

10 / 31

12

f1

f2

U

U

U

Δ

=

−

12

f1

f2

U

U

U

δ

=

−

Definicje

Definicje

Stratą napięcia

ΔU

12

nazywa się różnicę geometryczną napięć w

dwóch punktach (węzłach) sieci 1 i 2:

Spadkiem napięcia

nazywa się algebraiczną różnicę napięć w

dwóch punktach sieci:

Strata napięcia w linii jest
równa sumie geometrycznej
czynnej i biernej straty
napięcia:

L

L

12

R

X

U

U

U

I(R

j X )

Δ

= Δ

+ Δ

=

+

11 / 31

Podłużną stratą napięcia

ΔU’ w linii przesyłowej nazywa się rzut

wektora całkowitej straty napięcia

ΔU na kierunek osi rzeczywistych

(kierunek odniesienia).

Poprzeczną stratą napięcia

ΔU” nazywa się rzut wektora całkowitej

straty napięcia na kierunek osi urojonych (prostopadły do kierunku
odniesienia).

Czynną stratą napięcia

nazywa się stratę napięcia na rezystancji linii:

L

R

U

I R

Δ

= ⋅

Bierną stratą napięcia

nazywa się stratę napięcia na reaktancji linii:

L

X

U

I jX

Δ

= ⋅

Sk

Sk

ł

ł

adowe wektora straty

adowe wektora straty

12 / 31

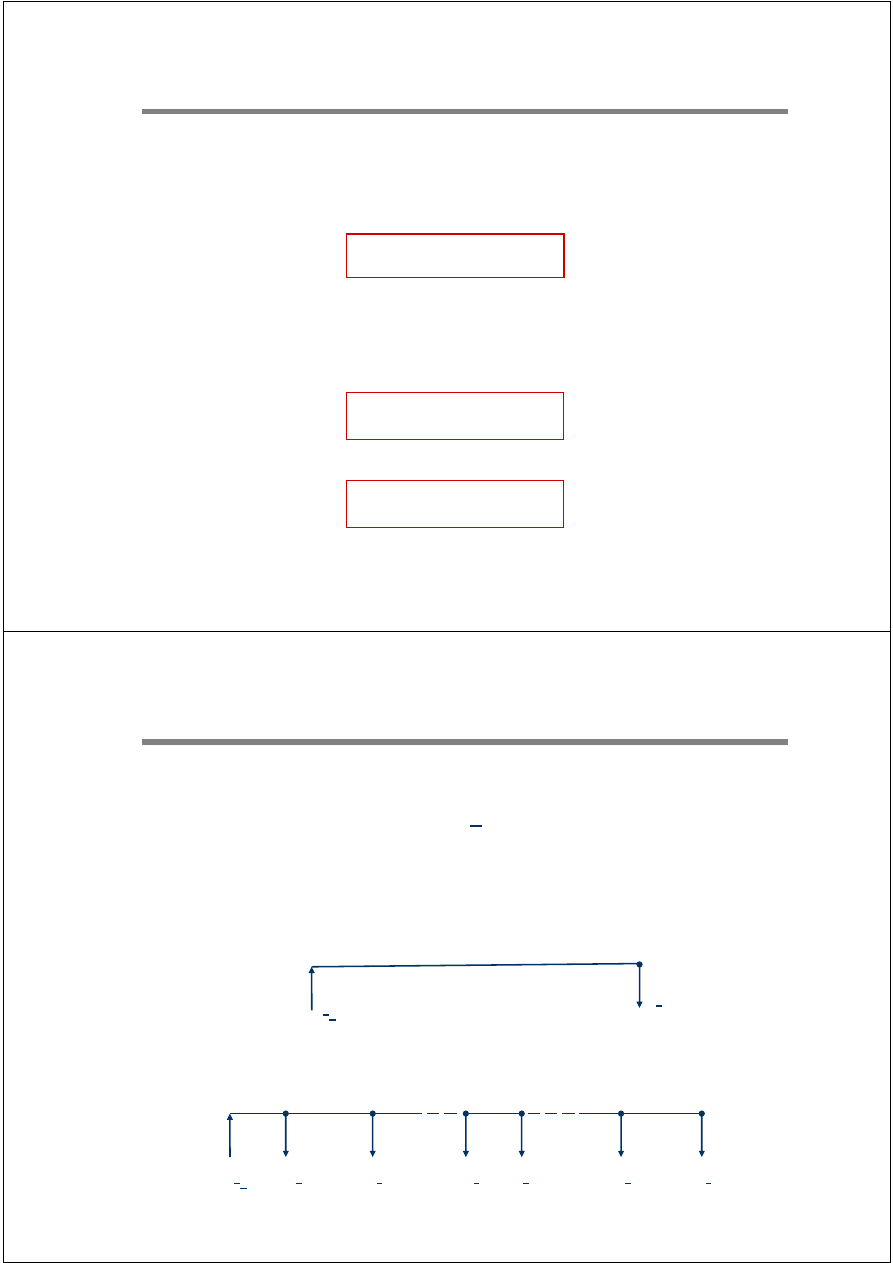
Strata a spadek

Strata a spadek

Na tym slajdzie powinny znaleźć się wykresy wskazowe samodzielnie narysowane przez studenta
dla obciążenia indukcyjnego i pojemnościowego.

13 / 31

Strata a spadek

Strata a spadek

Jeżeli obciążenie ma charakter indukcyjny to składowa urojona prądu
jest ujemna, a prąd bierny i moc bierna są dodatnie.
Wówczas:

U

f1

> U

f2

i

δU > 0

Jeżeli obciążenie ma charakter pojemnościowy to składowa urojona
prądu jest dodatnia, a prąd bierny i moc bierna są ujemne.

Stąd:

U

f1

< U

f2

i

δU < 0

Możliwy jest przypadek, że:

U

f1

= U

f2

i

δU = 0

14 / 31

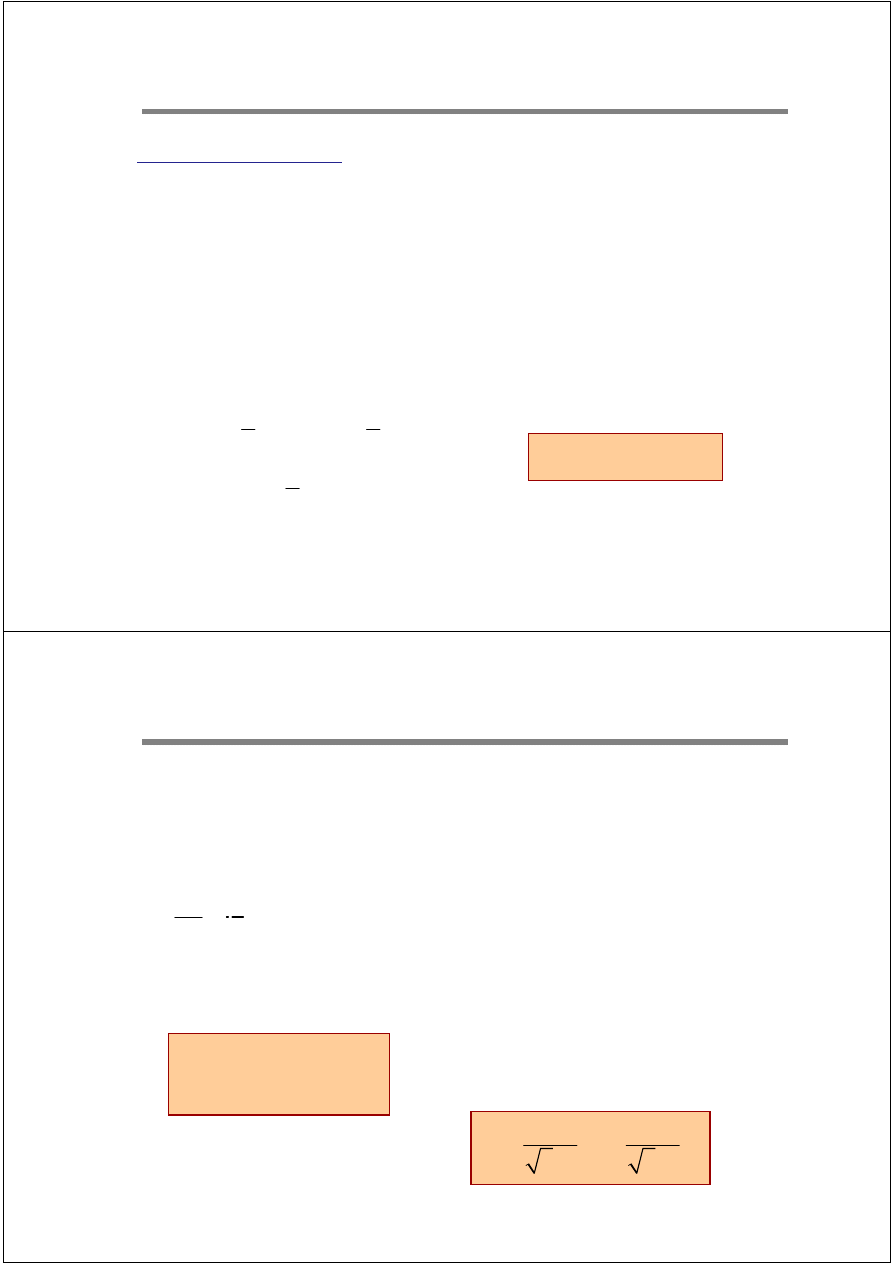
Spadek napi

Spadek napi

ę

ę

cia w linii I i II rodzaju

cia w linii I i II rodzaju

Podany zostanie sposób obliczania spadku napięcia przy
dowolnym obciążeniu dla linii:

¾

zasilającej

¾

rozdzielczej

Jako przypadek ogólniejszy zostanie rozważona linia II-go rodzaju.
Dla linii I-go rodzaju należy przyjąć Z

L

= R

L

.

0

1

I

0

I

1

0

1

2

α-1

α

n-1

n

I

0

I

1

I

2

I

α-1

I

α

I

n-1

I

n

15 / 31

-

f1

f2

'

'

U ad U

U

ad ac c d

δ =

=

=

+

c 'd c 'c * tg

oc ' tg * tg

2

2

δ

δ

=

=

δ

tg

0,5tg

2

δ

=

δ

2

c 'd 0,5 oc ' tg

=

δ

Spadek napi

Spadek napi

ę

ę

cia w linii zasilaj

cia w linii zasilaj

ą

ą

cej

cej

dla małych

δ

więc

δU = ac’ = ΔU’

Można przyjąć c’d = 0.
Stąd:

Spadek napięcia równy jest

podłużnej stracie napięcia

Obciążenie indukcyjne

Wykres wskazowy

16 / 31

( )

(

)

(

)

-

'

"

'

"

'

"

L

L

L

L

L

L

L

'

"

U IZ

I jI R

jX

I R I X

j I X

I R

U

j U

Δ =

= +

+

=

+

+

=

= Δ + Δ

-

'

'

"

L

L

cz L

b L

U

U I R I X

I R

I X

δ = Δ =

=

=

+

Spadek napi

Spadek napi

ę

ę

cia w linii zasilaj

cia w linii zasilaj

ą

ą

cej

cej

Wykorzystując powyższe założenie można określić praktyczny
wzór na spadek napięcia.

Ponieważ całkowita strata napięcia:

Stąd

Jeżeli odbiornik określony jest
wartościami mocy czynnej i biernej,
wówczas wzór na spadek napięcia
można zapisać w postaci:

L

L

n

n

P

Q

U

R

X

3U

3U

δ =

+

17 / 31

-

-

p

1

2

f1

f2

U

U U

3 U

3 U

3 U

δ

=

=

=

δ

p

%

n

U

U

100

U

δ

δ

=

⋅

%

L

L

n n

n n

L

L

2

2

n

n

P

Q

U

3

R

3

X 100

3U U

3U U

P

Q

R

X 100

U

U

⎛

⎞

δ

=

+

=

⎜

⎟

⎜

⎟

⎝

⎠

⎛

⎞

=

+

⎜

⎟

⎜

⎟

⎝

⎠

W obliczeniach praktycznych operuje się procentowym spadkiem
napięcia, odniesionym do napięcia znamionowego.

Spadek przewodowy:

lub:

Spadek napi

Spadek napi

ę

ę

cia w linii zasilaj

cia w linii zasilaj

ą

ą

cej

cej

18 / 31

(

)

(

)

n

'

'

"

0n

0n

-1,

-1,

-1,

-1,

1

n

cz -1,

-1,

b -1,

-1,

1

U

U

I

R

-I

X

I

R

I

X

α α α α α α α α

α=

α α α α

α α α α

α=

δ

= Δ

=

=

=

+

∑

∑

Spadek napi

Spadek napi

ę

ę

cia w linii rozdzielczej

cia w linii rozdzielczej

Spadek napięcia w całej linii równa się sumie spadków
napięcia na poszczególnych jej odcinkach:

Metoda

„sumowania odcinkami”

0

1

2

α-1

α

n-1

n

I

0

I

1

I

2

I

α-1

I

α

I

n-1

I

n

19 / 31

(

)

n

n

0n%

0

0

0

0

2

2

2

1

1

n

n

n

P

Q

100

U

R

X

* 100

P R

Q X

U

U

U

α

α

α

α

α

α

α

α

α=

α=

⎛

⎞

δ

=

+

=

+

⎜

⎟

⎜

⎟

⎝

⎠

∑

∑

Pamiętając, że prądy w gałęziach wynikają z sumowania prądów
odbiorów

-

n

1,

j

j

I

I

α α

=α

=

∑

można wyrazić spadek napięcia w zależności od prądów odbiorów,
a nie linii:

(

)

(

)

-

n

n

0n

0

0

cz

0

b

0

1

1

U

I' R

I'' X

I

R

I

X

α

α

α

α

α

α

α

α

α=

α=

δ

=

=

+

∑

∑

Metoda

„sumowania momentami”

lub w zależności od mocy odbiorów:

Spadek napi

Spadek napi

ę

ę

cia w linii rozdzielczej

cia w linii rozdzielczej

20 / 31

Spadek napi

Spadek napi

ę

ę

cia w linii III rodzaju

cia w linii III rodzaju

Linia zasilająca, obciążona mocą czynną i bierną indukcyjną

Wykres wskazowy

21 / 31

'

"

L L L L

U ac ' I R -I X

δ ≠

=

f1

f2

U U -U

δ =

Spadek napi

Spadek napi

ę

ę

cia w linii III rodzaju

cia w linii III rodzaju

Dla linii III-go rodzaju kąt

δ jest na

tyle duży, że nie można pominąć
odcinka c’d, a zatem:

Najłatwiej obliczyć spadek napięcia w linii III rodzaju określając
dowolną metodą moduł wektora napięcia na początku linii U

f1

, a

następnie obliczając spadek napięcia z jego definicji:

22 / 31

(

)

⎛

⎞

δ =

+

=

+

⎜

⎟

⎝

⎠

cz

L

b

L

L

L

n

n

P

Q

U

2 I R

I X

2

R

X

U

U

⎛

⎞

δ

=

+

⎜

⎟

⎝

⎠

%

L

L

2

2

n

n

P

Q

U

2

R

X

U

U

Spadek napi

Spadek napi

ę

ę

cia w linii jednofazowej

cia w linii jednofazowej

Obliczenia spadków, jak również strat napięcia w linii jednofazowej
przeprowadza się tak samo jak w linii trójfazowej pamiętając jednak,
że prąd obciążenia I płynie w tym przypadku

dwoma przewodami

linii.

Wobec tego, jeżeli R

L

i X

L

są odpowiednio rezystancją i reaktancją

jednego przewodu linii oraz oba przewody są jednakowe, to spadek
napięcia określony jest wzorem:

23 / 31

δ

=

=

+

'

"

T

2

T

2

T

2cz

T

2b

T

U

I R - I X

I

R

I X

1

2

3

I

I

I

= +

δ

=

+

'

"

'

"

T12

1

T1

1

T1

2

T2

2

T2

U

I R - I X

I R

- I X

δ

=

+

'

"

'

"

T13

1

T1

1

T1

3

T3

3

T3

U

I R - I X

I R - I X

Spadek napi

Spadek napi

ę

ę

cia w transformatorze

cia w transformatorze

Przy obliczaniu spadków napięcia w transformatorze pomija się
gałąź magnesującą schematu zastępczego. Wówczas schemat ten
ma taką samą postać jak schemat zastępczy linii II rodzaju.
Wobec tego:

Dla transformatora dwuuzwojeniowego:

Dla transformatora 3-uzwojeniowego:

24 / 31

dl

dl

U

jIX

Δ

=

δ

=

ϕ =

dl

dl

b

dl

U

I X sin

I X

Spadek napi

Spadek napi

ę

ę

cia na d

cia na d

ł

ł

awiku

awiku

Strata napięcia na dławiku:

Spadek napięcia:

Obliczanie strat mocy i energii

Obliczanie strat mocy i energii

26 / 31

2

P 3I R

Δ =

A

P t

Δ = Δ ⋅Δ

Straty w przewodach

Straty w przewodach

Straty mocy w układzie 3-fazowym:

Straty energii przy stałym obciążeniu w czasie

Δt = t

2

- t

1

:

Obciążenie stałe P = const.

Energia pobrana w czasie

Δt = t

2

- t

1

:

A P t

= ⋅Δ

27 / 31

Obciążenie zmienne P = f(t)

P

max

T

Pmax

t

P

2

1

t

t

t

A

P dt

=

∫

Energia pobrana w czasie

Δt = t

2

- t

1

:

max Pmax

A P

T

=

lub

2

1

max

t

t

t

P

max

P dt

T

P

=

∫

Z porównania wzorów:

Czas trwania mocy maksymalnej T

Pmax

jest to

zastępczy czas, w którym musiałoby trwać
obciążenie maksymalne, aby wydzieliła się taka
sama ilość energii jak przy obciążeniu zmiennym.

Straty w przewodach

Straty w przewodach

28 / 31

Δ = Δ

τ

max

A

P

Z porównania wzorów

Przy obciążeniu zmiennym określa się maksymalne straty mocy:

2

max

max

P

3I

R

Δ

=

Straty energii

2

1

t

t

t

A

P dt

Δ = Δ

∫

lub

Δ

τ =

Δ

∫

2

1

t

t

t

max

P dt

P

Czas trwania maksymalnych strat

τ jest to

zastępczy czas, w którym musiałyby trwać
straty mocy maksymalne, aby straty energii
były takie same jak przy obciążeniu
zmiennym.

Straty w przewodach

Straty w przewodach

29 / 31

Straty w transformatorach

Straty w transformatorach

1. straty w przewodach uzwojenia, zwane stratami w miedzi lub

stratami obciążeniowymi,

2. straty w rdzeniu żelaznym, zwane krótko stratami w żelazie

lub stratami jałowymi.

Straty mocy

Straty mocy w transformatorach dzieli się na 2 grupy:

Straty jałowe

są proporcjonalne do kwadratu napięcia i nie zależą od

obciążenia. Ponieważ w normalnych warunkach ruchowych napięcie
nie ulega większym zmianom, dlatego też straty jałowe uważa się za
stałe. Wartość tych strat podawana jest w katalogach.

30 / 31

Δ

=

2

o

t

P

3I R

Δ

=

2

on

n

t

P

3I R

⎛ ⎞

⎛

⎞

Δ

= Δ

= Δ

⎜ ⎟

⎜

⎟

⎝ ⎠

⎝

⎠

2

2

o

on

on

n

n

I

S

P

P

P

I

S

Straty obciążeniowe

są wynikiem przepływu prądu przez uzwojenie,

a więc wyraża się je taką samą zależnością, jak straty w przewodach:

Przy obciążeniu znamionowym:

Dzieląc stronami powyższe równania otrzymuje się:

Wzór powyższy pozwala na obliczenie strat przy dowolnym
obciążeniu w zależności od strat przy obciążeniu znamionowym, które
podawane są w katalogach.

Straty w transformatorach

Straty w transformatorach

31 / 31

⎛

⎞

Δ = Δ + Δ

⎜

⎟

⎝

⎠

2

t

j

on

n

S

P

P

P

S

⎛

⎞

Δ

= Δ ⋅

+ Δ

τ

⎜

⎟

⎝

⎠

2

max

T

j

on

n

S

A

P 8760

P

S

Straty w transformatorach

Straty w transformatorach

Łączne straty w transformatorze są sumą strat jałowych i
obciążeniowych:

Zwykle oblicza się roczne straty energii. Jeśli transformator pracuje
w sposób ciągły to straty jałowe trwają 8760 h/a. Straty
obciążeniowe oblicza się mnożąc maksymalne straty mocy przez
czas trwania maksymalnych strat:

Straty energii